Deep Learning資格試験 深層学習 最適化・高速化・軽量化
はじめに
日本ディープラーニング協会の Deep Learning 資格試験(E 資格)の受験に向けて、調べた内容をまとめていきます。
初期値の設定方法
通常(正規分布に従った重み)
Xavier
対象の活性化関数
- シグモイド関数
- 双曲線正接関数
設定方法
- 重みの要素を、前の層のノード数の平方根で除算した値
He
対象の活性化関数
- ReLU 関数
設定方法
- 重みの要素を、前の層のノード数の平方根で除算した値に対し
\sqrt{2}
ドロップアウト
- 過学習の課題
- ノードの数が多い
- ドロップアウトとは︖
- ランダムにノードを削除して学習させること
- メリット
- データ量を変化させずに、異なるモデルを学習させていると解釈できる
ソースコード
コード実装
ソースコードはゼロから作る Deep Learningから引用
import numpy as np
class Dropout:
"""
http://arxiv.org/abs/1207.0580
"""
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
Weight decay(荷重減衰)
- eight decay とは、簡単に言えば、重みパラメータの値が小さくなるように学習を行う事を目的とした手法。
- 重みの値を小さくすることで、過学習が起きにくくなる。
- 重みを小さいに値にしたければ、初期値もできるだけ小さい値からスタートするのが正攻法である。ただし、重みの初期値をすべて0に設定すると、正しい学習が行えない。重みの初期値を0にすると、誤差逆伝播法において、全ての重みの値が均一に(同じように)更新されてしまうため。
- この「重みが均一になってしまうこと」を防ぐ(正確には、重みの対照的な構造を崩す)ために、ランダムな初期値が必要である。
過学習の原因
- 重みが大きい値をとることで、過学習が発生することがある。
- 学習させていくと、重みにばらつきが発生する。
- 重みが大きい値は、学習において重要な値であり、重みが大きいと過学習が起こる。
⇒ 一部のデータに対して極端な反応を示している状態が、過学習の状態ということになる。
過学習の解決策
- 誤差に対して、正則化項を加算することで、重みを抑制する
- 過学習がおこりそうな重みの大きさ以下で重みをコントロールし、かつ重みの大きさにばらつきを出す必要がある。
早期終了(early stopping)
- ニューラルネットワークなどの訓練時に用いられる学習テクニック
- 事前に訓練終了条件を定めておき、訓練過程においてその条件に達すると訓練を終了させる。
- 訓練集合への過剰適合が抑制される。
- パラメータにある種の制約を課していると考えられるため、正則化の一種であると解釈できる。
- 2次の誤差関数を持つ単純な線形モデルを単純な勾配降下法で最適化するとき、早期終了はリッジ正則化と同等な効果を示す場合がある。
一般的な手順
- 訓練時に、エポック毎に誤差を算出する。
- 誤差が前のステップより小さくならなかったら1カウントする。
- そのカウント総数が所定の値を超えたら訓練終了する。
最適化戦略
バッチ正規化
- バッチ正規化とは︖
- ミニバッチ単位で、入力値のデータの偏りを抑制する手法
- 学習を早く進行させられる。(学習率を大きくできる)
- 重みの初期値にそれほど依存しない
- 過増適合を抑制する
- バッチ正規化の使い所とは︖
- 活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える。
- ミニバッチに含まれる sample の同⼀チャネルが同⼀分布に従うよう正規化
-
H \times W \times C N N - RGB の 3 チャネルの sample が
N
-
- 問題点
- Batch Size が⼩さい条件下では、学習が収束しないことがある。
- RNN への適用方法があきらかになっていない。
処理
バッチ正規化層では、下記の式でノードの入力値を正規化する。
バッチ正規化の数学的記述
ミニバッチの平均
ミニバッチの分散
ミニバッチの正規化
変倍・移動
処理および記号の説明
ソースコード
コード実装
ソースコードはゼロから作る Deep Learningから引用
import numpy as np
class BatchNormalization:
"""
http://arxiv.org/abs/1502.03167
"""
def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
self.gamma = gamma
self.beta = beta
self.momentum = momentum
self.input_shape = None # Conv層の場合は4次元、全結合層の場合は2次元
# テスト時に使用する平均と分散
self.running_mean = running_mean
self.running_var = running_var
# backward時に使用する中間データ
self.batch_size = None
self.xc = None
self.std = None
self.dgamma = None
self.dbeta = None
def forward(self, x, train_flg=True):
self.input_shape = x.shape
if x.ndim != 2:
N, C, H, W = x.shape
x = x.reshape(N, -1)
out = self.__forward(x, train_flg)
return out.reshape(*self.input_shape)
def __forward(self, x, train_flg):
if self.running_mean is None:
N, D = x.shape
self.running_mean = np.zeros(D)
self.running_var = np.zeros(D)
if train_flg:
mu = x.mean(axis=0)
xc = x - mu
var = np.mean(xc**2, axis=0)
std = np.sqrt(var + 10e-7)
xn = xc / std
self.batch_size = x.shape[0]
self.xc = xc
self.xn = xn
self.std = std
self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu
self.running_var = self.momentum * self.running_var + (1-self.momentum) * var
else:
xc = x - self.running_mean
xn = xc / ((np.sqrt(self.running_var + 10e-7)))
out = self.gamma * xn + self.beta
return out
def backward(self, dout):
if dout.ndim != 2:
N, C, H, W = dout.shape
dout = dout.reshape(N, -1)
dx = self.__backward(dout)
dx = dx.reshape(*self.input_shape)
return dx
def __backward(self, dout):
dbeta = dout.sum(axis=0)
dgamma = np.sum(self.xn * dout, axis=0)
dxn = self.gamma * dout
dxc = dxn / self.std
dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0)
dvar = 0.5 * dstd / self.std
dxc += (2.0 / self.batch_size) * self.xc * dvar
dmu = np.sum(dxc, axis=0)
dx = dxc - dmu / self.batch_size
self.dgamma = dgamma
self.dbeta = dbeta
return dx
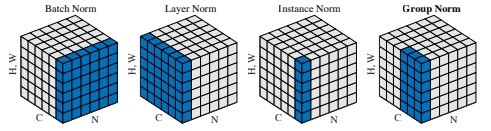
Layer 正規化
- 同じ層内の全てのユニットを対象として計算するため、ミニバッチ内の個々のデータごとに正規化に用いる平均と標準偏差が異なる。
- それぞれの sample の全ての pixels が同⼀分布に従うよう正規化
- N 個の sample のうち⼀つに注⽬。H x W x C の全ての pixel が正規化の単位。
- RGB の 3 チャネルの sample が N 個の場合は、ある sample を取り出し、全てのチャネルの平均と分散を求め正規化を実施 (図の⻘い部分に対応)。特徴マップごとに正規化された特徴マップを出⼒
- ミニバッチの数に依存しないので、上記の問題を解消できていると考えられる。
Instance 正規化
- さらに channel も同⼀分布に従うよう正規化
- 各 sample をチャンネルを ごとに正規化
- コントラストの正規化に寄与・画像のスタイル転送やテクスチャ合成タスクなどで利用
Group 正規化
参考:Group Normalizationから引用
高速化
データ並列化
- 親モデルを各ワーカーに⼦モデルとしてコピー(ワーカーがコンピューターにあたる)
- データを分割し、各ワーカーごとに計算させる。
- データ並列化は各モデルのパラメータの合わせ⽅で、同期型か⾮同期型か決まる。
データ並列化: 同期型
パラメータ更新の流れ:各ワーカーが計算が終わるのを待ち、全ワーカーの勾配が出たところで勾配の平均を計算し、親モデルのパラメータを更新する。
データ並列化: ⾮同期型
パラメータ更新の流れ:各ワーカーはお互いの計算を待たず、各子モデルごとに更新を行う。学習が終わった子モデルはパラメータサーバに Push される。新たに学習を始める時は、パラメータサーバから Pop したモデルに対して学習していく。
同期型と⾮同期型の⽐較
- 処理のスピードは、お互いのワーカーの計算を待たない⾮同期型の⽅が早い。
- ⾮同期型は最新のモデルのパラメータを利⽤できないので、学習が不安定になりやすい。
- Stale Gradient Problem
- 現在は同期型の⽅が精度が良いことが多いので、主流となっている。
モデル並列化
- 親モデルを各ワーカーに分割し、それぞれのモデルを学習させる。全てのデータで学習が終わった後で、⼀つのモデルに復元する。
- モデルが⼤きい時はモデル並列化を、データが⼤きい時はデータ並列化をすると良い。
- モデルのパラメータ数が多いほど、スピードアップの効率も向上する。
軽量化
モデルの精度を維持しつつパラメータや演算回数を低減する⼿法の総称
- ⾼メモリ負荷 ⾼い演算性能が求められる。
- 低メモリ 低演算性能での利⽤が必要とされる。(IoT など)
量子化
- ネットワークが⼤きくなると⼤量のパラメータが必要なり学習や推論に多くのメモリと演算処理が必要
- 通常のパラメータの 64 bit 浮動⼩数点を 32 bit など下位の精度に落とすことでメモリと演算処理の削減を⾏う
利点
- 計算の⾼速化
- 倍精度演算(64 bit)と単精度演算(32 bit)は演算性能が⼤きく違うため、量⼦化により精度を落とすことによりより多くの計算をすることができる。
- 深層学習で⽤いられる NVIDIA 社製の GPU の性能は下記のようになる。
- 省メモリ化
- ニューロンの重みを浮動小数点の bit を少なくし有効桁数を下げることで、ニューロンのメモリサイズを小さくすることができ、メモリ使用量を抑えることができる。
⽋点
- 精度の低下
- ニューロンが表現できる少数の有効桁数が小さくなるため
蒸留
モデルの簡約化
学習済みの精度の⾼いモデルの知識を軽量なモデルへ継承させる。知識の継承により、軽量でありながら複雑なモデルに匹敵する精度のモデルを得ることが期待できる。
教師モデルと⽣徒モデル
- 蒸留は教師モデルと⽣徒モデルの 2 つで構成される
- 教師モデルの重みを固定し⽣徒モデルの重みを更新していく誤差は教師モデルと⽣徒モデルのそれぞれの誤差を使い重みを更新していく
教師モデル
予測精度の⾼い、複雑なモデルやアンサンブルされたモデル
⽣徒モデル
教師モデルをもとに作られる軽量なモデル
生徒を学習させるための損失
温度付きソフトマックス関数
蒸留の利点
蒸留によって少ない学習回数でより精度の良いモデルを作成することができている
プルーニング
計算の⾼速化
寄与の少ないニューロンの削減を行い、モデルの圧縮を行うことで高速に計算できる。
ニューロンの削減の⼿法は重みが閾値以下の場合ニューロンを削減し、再学習を⾏う。
例として、重みが 0.1 以下のニューロンを削減する。
Discussion