代表値
代表値
ある一群の数字(データ)をただ1つの数字で代表させて全体的な性質を判断するために用いられるもの
算術平均
全体でn個のデータがあるとする。
\bar {x} = \frac {x_{1} + x_{2} + \cdots + x_{n}}{n} = \frac {1}{n} \sum _{i=1}^{n}{x_{i}}
算術平均の重要な性質
- データの1次式の算術平均は算術平均についての同じ1次式である
- 算術平均からの偏差の和は常に0である
- 算術平均からの偏差の平方和は他のいかなる一定値からの偏差の平方和よりも小である
1.データの1次式の算術平均は算術平均についての同じ1次式である
データx_i \quad (i = 1, \dots, n)をy_iに変換する。(これを1次変換という。)
このとき変換されたデータy_iの算術平均\bar {y}は、
\bar {y} = a \bar {x} + b
となる。すなわち、算術平均は1次変換を保持する。
※算術平均は1次変換を保持する
個々のデータx_iとy_iの間の1次関係式が両者の算術平均の間にも成立する
証明
\begin{aligned}
\bar {y} & = \frac {1}{n} \sum _{i=1}^{n}{y_i} \\
& = \frac {1}{n} \sum _{i=1}^{n}{\left( a x_i + b \right)} \\
& = \frac {a}{n} \sum _{i=1}^{n}{x_i} + \frac {1}{n} \sum _{i=1}^{n}{b} \\
& = a \bar {x} + b
\end{aligned}
2.算術平均からの偏差の和は常に0である
\sum _{i=1}^{n}{\left( x_i - \bar {x} \right)} \equiv 0
偏差
個々のデータx_iが平均値\bar {x}からどれだけ離れているかを表す
証明
\sum _{i=1}^{n}{\left( x_i - \bar {x} \right)} = \sum _{i=1}^{n}{x_i} - \sum _{i=1}^{n}{\bar {x}}
算術平均の式より、n \bar {x} = \sum _{i=1}^{n}{x_i}。よって、
n \bar {x} - n \bar {x} = 0
3.算術平均からの偏差の平方和は他のいかなる一定値からの偏差の平方和よりも小である
いま、aをある定数とするとき、aがいかなる値であっても、
\sum _{i=1}^{n}{\left( x_{i} - \bar {x} \right)^{2}} \le \sum _{i=1}^{n}{\left( x_i - a \right)^{2}}
が成り立つ。上式で等号が成り立つのは、a = \bar {x}のときだけ。
証明
\begin{aligned}
\sum {\left(x_i - a\right)^{2}} & = \sum {\left( x_i - \bar {x} + \bar {x} - a \right)^{2}} \\
& = \sum {\left( x_i - \bar {x} \right)^{2}} + \sum {\left( \bar {x} - a \right)^{2}} + \sum {2\left( x_i - \bar {x} \right) \left( \bar {x} - a \right)} \\
& = \sum {\left( x_i - \bar {x} \right)^{2}} + n \left( \bar {x} - a \right)^{2} + 2 \left( \bar {x} - a \right) \sum {\left( x_i - \bar {x} \right)}
\end{aligned}
算術平均からの偏差の和は常に0であるため、上式の第3項は0となる。
\sum {\left( x_i - a \right)^{2}} = \sum {\left( x_i - \bar {x} \right)^{2}} + n \left( \bar {x} - a \right)^{2}
上記の第2項は、n \left( \bar {x} - a \right)^{2} \ge 0なので
\sum _{i=1}^{n}{\left( x_i - a \right)^{2}} \ge \sum _{i=1}^{n}{\left( x_{i} - \bar {x} \right)^{2}}
また、「算術平均は偏差の平方和を最小にするような値である」ともいえる。
S\left( a \right) = \sum _{i=1}^{n}{ \left( x_i - a \right)^{2} }
証明
このS\left(a\right)を最小にするようなaの値を求める。
この2次関数は正の関数なので、極値は極小となる。この関数をaで微分したものを0として求められる。
\begin{aligned}
S\left( a \right) & = - 2 \sum {\left( x_i - a \right)} & = 0 \\
& = - 2\left( \sum {x_i} - \sum {a} \right) & = 0 \\
n \bar {x} & = n a \\
\bar {x} & = a
\end{aligned}
幾何平均(geometric mean)
平均成長率を求めるとする。いま第i年の成長率をg_i(%)とし、初期年におけるGDPの値をY_0とすれば、n年後のGDPの値Y_nは
Y_{n} = Y_{0} \left(1+ g_{1}\right) \cdots \left(1+ g_{n}\right) \quad (1.4)
となる。また、この期間に毎年一定の成長率で成長したとし、その率をgとすれば、
Y_{n} = Y_{0} \left(1+ g\right)^{n} \quad (1.5)
である。このgが平均成長率である。したがってgは式(1.4)と式(1.5)が等しくおいて、
\begin{aligned}
Y_{0} \left(1+ g\right)^{n} & = & Y_{0} \left(1+ g_{1}\right) \cdots \left(1+ g_{n}\right) \\
1 + g & = & \sqrt[n]{ \left(1+ g_{1}\right) \cdots \left(1+ g_{n}\right) }
\end{aligned}
と求められる。 m_{g} = 1 + g,x_{i} = \left(1 + g_{i}\right)とすると
m_{g} = \sqrt [n]{x_{1} \cdots x_{n}} = \left( \prod _{i=1}^{n}{x_{i}} \right)^{\frac {1}{n}}
が得られる。このような幾何平均は、一般にデータが比率である場合に適当な平均と考えられる。
調和平均(harmonic mean)
典型的には、率の平均が望まれているような状況で調和平均が適切である。 正の実数について、調和平均は算術平均の逆数として定義される。
m_{H} = \frac {1}{ \frac {1}{n} \left( \frac {1}{x_{1}} + \cdots + \frac {1}{x_{n}} \right) } = \frac {1}{ \frac {1}{n} \sum _{i=1}^{n}{\left( \frac {1}{x_{i}} \right)} }
絶対平均(mean absolute value)
大きさの平均を求めたい場合に使用。
- 絶対値を用いてデータの正負の符号をなくす。
- 絶対値の算術平均
m_{A} = \frac {1}{n} \sum _{i=1}^{n}{\left| x_{i} \right|}
RMS(root mean square)
大きさの平均を求めたい場合に使用。
- 絶対値の代わりに2乗によって正負の符号の差をなくす。
- 標準偏差はRMSの一種
- データの2乗の値の算術平均を求めて平方根をとる
m_{RS} = \sqrt {\frac {1}{n} \sum _{i=1}^{n}{ x_{i}^{2} }}
加重平均(weighted arithmetic mean)
データxに対してウェイト(重み)付けを行い、その平均を求める。
以下の場合には、加重平均を用いる。
- 離散的なデータである
- 同じ観測値をとる個体が複数存在する
\bar {x_{w}} = \frac { \sum _{i=1}^{n}{w_{i}x_{i}} }{ \sum _{i=1}^{n}{w_{i}} }
なお、重みの合計が1になるように決められるのが普通である。
そのときには、加重平均は次のように書ける。このときのw_iは割合になる。
\bar {x_{w}} = \sum {w_i x_i}
データを大きさの順に並べたときちょうど中央に位置するデータの値
データが奇数の場合: x_{1}, \dots, x_{(n+1)/2}, \dots, x_{n+1}
\mathrm {Median} = x_{(n+1)/2}
データが偶数の場合: x_1, \dots, x_{n/2}, x_{(n+1)/2}, \dots, x_n
\mathrm {Median} = \frac {\left( x_{n/2} + x_{(n+1)/2} \right)}{2}
モード、最頻値(mode)
最も数多くのデータが集中しているある特定の値
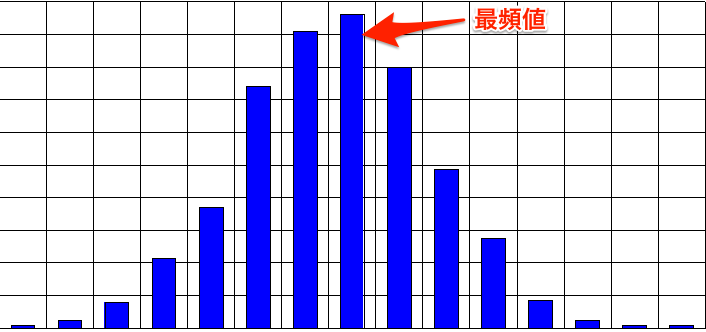
散らばりの尺度
分散度
一群全体における各値(データ)の差の程度。ばらつき、散らばり
範囲(range)
最高値と最低値の差
四分位偏差
四分位数・・・全体のデータを小さい方から順に並べたとき、データ数を4等分する位置の値。四分位数は3つある。
-
Q_1: 第1四分位数
-
Q_2: 第2四分位数
-
Q_3: 第3四分位数
QD = \frac {Q_3 - Q_1}{2}
四分位数の求め方


データの分析(四分位数・四分位範囲・四分位偏差)より引用
平均絶対偏差
平均点からどれだけ離れているかという大きさに関心があるため、偏差(x_i - x)の絶対値をとる。
\left| x_i - \bar {x} \right| \quad (i = 1,2,\cdots)
平均絶対偏差(=MD)は各データが平均値から大体平均してどれだけ分散しているかを表す。
\mathrm {MD} = \frac {1}{n} \sum _{i=1}^{n}{\left| x_i - \bar {x} \right|}
平均絶対偏差が大きくなるほど、分散度が大
標準偏差
平均値からの偏差の2乗を算術平均し、それをもとのデータと同次元の量に戻すために平方を開いたもの。RMSの一種。
\sigma = \sqrt {\frac {1}{n} \sum _{i=1}^{n}{\left( x_i - \bar {x} \right)^{2}}}
標準偏差\sigmaは、
- 平均値からの偏差のRMS(平方平均の平方根)
- 偏差の大きさの平均
分散
標準偏差を2乗した値
{\sigma}^{2} = \frac {1}{n} \sum _{i=1}^{n}{\left( x_i - \bar {x} \right)^{2}}
- 標準偏差と分散はともに負になることはなく、それらが0になるのはすべてのデータx_iが等しく、平均値\bar {x}に等しいときのみ。
標準偏差および分散の重要な性質
データの一次変換と分散(標準偏差)
もとのデータx_i \quad (i=1,2,\dots,n)を1次式
によって、y_iに1次変換するとき、
\sigma_{y} = \left| a \right| \sigma_{x}\\
\sigma_{y}^{2} = a^{2} \sigma_{x}^{2}
-
\sigma_{x}: データxの標準偏差
-
\sigma_{y}: データyの標準偏差
となる。
※重要
一次変換式のパラメータbは上式とは無関係。したがって、分散や標準偏差を計算する際にすべてのデータx_iなどに一定値(パラメータb)を加えても結果は同じである。
証明
\sigma_{y}^{2} = \frac {1}{n} \sum {\left( y_i - \bar {y} \right)^{2}}
\bar {y} = a \bar {x} + bより、
\begin{aligned}
\sigma_{y}^{2} & = \frac {1}{n} \sum {\left[ a x_i + b - \left( a \bar {x} + b \right) \right]^{2}}\\
& = \frac {1}{n} \sum {a^2 \left( x_i - \bar {x} \right)^2} \\
& = a^2 \cdot \frac {1}{n} \sum {\left( x_i - \bar {x} \right)^2}
\end{aligned}
データxの分散が\sigma_{x}^{2} = \frac {1}{n} \sum {\left( x_i - \bar {x} \right)^{2}}なので、
\sigma_{y}^{2} = a^2 \sigma_{x}^{2}
となる。
標準偏差は非負であるから、データxからデータyへの一次変換式のパラメーターaがa < 0の場合も考慮して、
\sigma_{y} = \sqrt {\sigma_{y}^{2}} = \left| a \right| \sigma_{x}
となる。
分散の計算式
{\sigma}^{2} = \frac {1}{n} \sum _{i=1}^{n}{x_{i}^{2}} - {\bar {x}}^{2}
分散の定義には「平均値からの偏差の2乗の平均」であるが、計算上は「2乗の平均値から平均値の2乗を引く」ことによって求められる。
証明
\begin{aligned}
{\sigma}^{2} & = \frac {1}{n} \sum {\left(x_i - \bar {x}\right)^2} \\
& = \frac {1}{n} \sum { x_{i}^{2} - 2 x_{i} \bar {x} + {\bar {x}}^2 } \\
& = \frac {1}{n} \sum {x_{i}^{2}} - 2 \bar {x} \frac {1}{n} \sum {x_i} + \frac {1}{n} \sum {{\bar {x}}^2} \\
& = \frac {1}{n} \sum {x_{i}^{2}} - 2 {\bar {x}}^{2} + {\bar {x}}^2 \\
& = \frac {1}{n} \sum {x_{i}^{2}} - {\bar {x}}^2
\end{aligned}
範囲と割合との対応
標準偏差は散らばりの1つの測度である。したがってその大きさがわかるということは、どのような範囲にデータがどのように散らばっているか(データの散らばりのことを分布という)が明らかになることを意味する。
平均値と標準偏差がわかるとデータの範囲と割合の大まかな対応がわかる。
| 範囲 |
割合 |
| \bar {x} \pm \frac {2}{3} \sigma |
約50% |
| \bar {x} \pm \sigma |
約67% |
| \bar {x} \pm 2 \sigma |
約95% |
| \bar {x} \pm 3 \sigma |
99~100% |
標準化変量と偏差値
あるデータが全体のデータの中でどれくらいの位置にあるかを知る
→そのデータが平均値から標準偏差の何倍だけ離れているかによっておおよその見当がつく
あるデータxが平均値\bar {x}から標準偏差の何倍離れているかという数値で表す。
x - \bar {x} = \sigma \cdot z
- 標準化・・・xをzに変換すること
- 標準化変量・・・z
z = \frac {x - \bar {x}}{\sigma}
-
\bar {z} = 0 :標準化変量の平均値は0
-
\sigma_{z}^{2} = 1 : 標準化変量の分散(標準偏差)は1
あるデータxの標準化(x->z)により、そのデータxが分布の上の相対的な位置の比較が可能になる
→zは平均値も標準偏差も異なるクラスの間でも比較が可能になる
「標準化変量の平均値は0」「標準化変量の分散(標準偏差)は1」の証明
\begin{aligned}
z & = \frac {x - \bar {x}}{\sigma} \\
& = \left( 1/\sigma \right) x - \left( \bar {x} / \sigma \right)
\end{aligned}
上式は、y_i = a x_i + bのa = \left( 1/\sigma \right),b = - \left( \bar {x} / \sigma \right)であり、1次変換であるため\bar {y} = a \bar {x} + bより
\begin{aligned}
\bar {z} & = \left(1/\sigma\right) \bar {x} - \left(\bar {x} / \sigma\right) \\
& = \left(\bar {x} / \sigma\right) - \left(\bar {x} / \sigma\right) \\
& = 0
\end{aligned}
よって、「標準化変量の平均値は0」である。
また、\sigma_{y}^{2} = a^2 \sigma_{x}^{2}より
\sigma_{z}^{2} = \left( 1/\sigma \right) \sigma_{x}^{2} = 1
「標準化変量の分散(標準偏差)は1」である。
変異係数
2つ以上の異なる標本の散らばりの大きさを比較する。
標準偏差はデータの散らばりの大きさを絶対的な大きさで表したものであり、データの平均的な大きさが大であれば、その散らばりも絶対的な大きさとしては大きくなるのが自然。
したがって、異なる標本の散らばりの大きさを比較するためには、標準偏差そのままではなく、それをデータの平均的大きさとの相対的関係で考えた尺度を用いる必要がある。
相対的分散度: 変動係数と呼ぶ
\mathrm {CV} = \frac {\sigma}{\bar {x}}
CVは通常その値を100倍した100分比で用いられる。(ex 40.7%)
変異係数を使う事例
犬や猫と馬や牛との間の体重の分散度を比較する



Discussion