👋

FEMM解析の結果をシミュレーションに使う

2024/01/02に公開

Python

1.FEMMの特徴としたいこと

FEMM解析は三角形のメッシュで解析が行われていてメッシュの切り方は選ぶことができない???
できるのかもしれないが、わからない...
自分のシミュレーションには直行のメッシュを使いたいので
適当な点で得られる結果をメッシュに落とし込みたい

解析結果のファイルは.ansファイルで得られるため、その中身からメッシュデータに変換して直交座標のデータを作成することをやっていきまーす。

2.FEMM解析結果 .ans ファイルの中身

まずは.ansの中身を見てみます。テキストファイルなので開くことができます。

こんな感じで始まり、最初は初期の設定が含まれます。そのあと、FEMMで入力した点や、線などの位置データが含まれます。

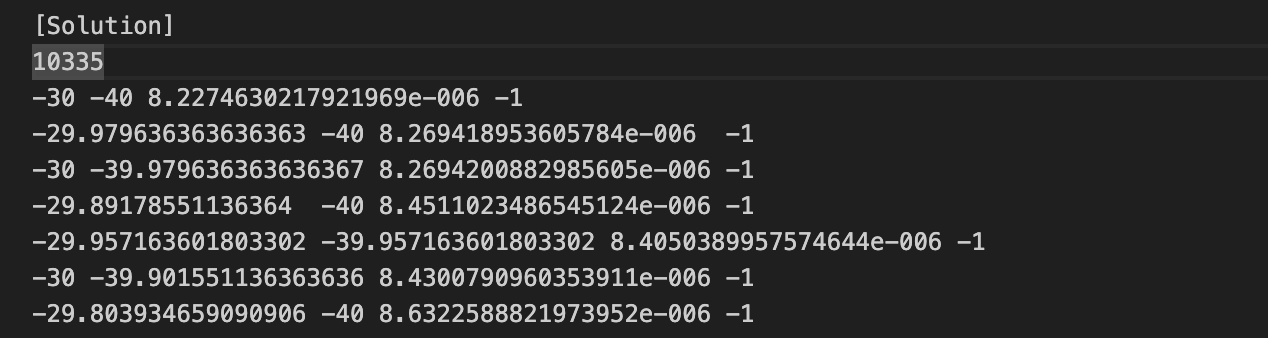
[Solution]
からが解析結果です。

1列目	2列目	3列目	4列目
x座標	y座標	ベクトルポテンシャル	よくわからない...

って感じのデータになっているっぽいです。

さらに下にもデータがありますが、よくわからない...
ベクトルポテンシャルがあれば磁場データは得られるでしょ!!!

3.データを読み込む

まず、結果の出力ファイル(.ans)をそのまま読み混むことができないので先ほどのデータ部分をコピーして別のファイルにでも書き出します。(手作業...)
pythonで読み込んでデータ処理しようとしたけどちょっと難しそうでした...めちゃくちゃコピーだるいので知ってる人いたら教えてください。

python

### データの読み込み　　###

import numpy as np
# データファイルのパス
file_path = 'test_1.dat'  
# ファイルをNumPy配列として読み込む
data = np.genfromtxt(file_path)

とりあえずデータ部分だけコピーして作成したファイル(.datにした)を読み込みます。
これで読み込めたと思います。

4.データの加工と描画

データを加工しつつ、描画していきたいと思います。

python

x = data[:,0]*0.1      # x [mm] -> [cm]
y = data[:,1]*0.1     # y[mm] -> [cm]
b_z = data[:,2]  #　ベクトルポテンシャル[Wb/m]

x = x + 2
y = y + 0.4   # したの壁面が0になるように

欲しいデータは[cm]のデータで、解析のときは[mm]でやってたので変換、ベクトルポテンシャルのデータの単位はどの時でも[Wb/m]です!!!(これ重要、めっちゃ探した)
あとは基準の位置とかを合わせてあげた。(xy座標)

python

###　　散布図でデータの値を確認　　###

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

# 散布図をプロット
sc = ax.scatter(x, y, c=b_z, cmap='jet')  

# カラーバーを追加
plt.colorbar(sc)

# タイトルとラベルを設定
ax.set_title('vector potensial')
ax.set_xlabel('x')
ax.set_ylabel('y')

# 表示
plt.show()

プロットしてみたらこんな感じ

5.点のデータを直行グリッドにする

まずは直交座標の欲しいデータを取っていきます。cell番号などね。

python

from scipy.interpolate import griddata

# 長さが一致していることを確認
assert len(x) == len(y) == len(b_z), "Lengths of x, y, and z must be equal"

# グリッドデータの生成
x_i = np.linspace(0, 7, 253)
y_j = np.linspace(0, 0.8, 61)
dx = x_i[1]
dy = y_j[1]
x_i = x_i - dx
y_j = y_j - dy
for i in range(3):
    i=i+1
    x_i = np.append(x_i,x_i[252] + dx*i)
    y_j = np.append(y_j, y_j[60] + dy*i)
x_all = np.zeros(257)
y_all = np.zeros(65)
x_all[0] = x_i[0]-dx
y_all[0] = y_j[0]-dy
for i in range(len(x_i)):
    x_all[i+1] = x_i[i]
for j in range(len(y_j)):
    y_all[j+1] =y_j[j]

こっから点データをグリッドの各点のデータに落としていきます。
プラズマ解析のperticle in cell法で用いる手法を真似してやりました。
今回は2次のスプラインを取って点データをグリッドデータにしていきます。
詳しくは以下のページ↓↓↓↓↓↓

今回は2次のスプラインがpythonのライブラリであるようなので使っていきます。変換して描画します。

python

x_i, y_j = np.meshgrid(x_all, y_all)
## ベクトルポテンシャルのグリッドデータを計算
z_i = griddata((x, y), b_z, (x_i, y_j), method='cubic')   ## 2次のスプラインらしい
### グリッドでのベクトルポテンシャルの描画  ###
plt.contourf(x_i, y_j, z_i, levels=15, cmap='jet')
plt.colorbar()
# plt.scatter(x, y, color='k')  # 元のデータポイントをプロット
plt.show()

これで欲しい部分のベクトルポテンシャルのグリッドデータを得られました。

磁場を求める

ベクトルポテンシャルと磁場の関係は

\bm{B}=\nabla ×\bm{A}

なので、

\begin{align}B_x&=\frac{\partial A_z}{\partial y}\\B_y&=-\frac{\partial A_z}{\partial x}\end{align}

これを実装すると

python

### 磁場をベクトルポテンシャルから求める　###

# 初期化
bs_x = np.zeros((len(x_i[:,0]), len(y_j[0,:])), dtype=np.float64)
bs_y = np.zeros((len(x_i[:,0]), len(y_j[0,:])), dtype=np.float64)

# 磁場の計算(前進差分)
for j in range(0,len(y_j[0,:])-1):
    for i in range(0,len(x_i[:,0])-1):
        bs_x[i,j] = (z_i[i+1,j]-z_i[i,j])/dy*100 # [T] 
        bs_y[i,j] = -(z_i[i,j+1]-z_i[i,j])/dx*100 #[T]
        

# 磁場の大きさ
bs_vol = (bs_x**2+bs_y**2)**0.5

##描画
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# ax.set_aspect(0.5)
cax = ax.pcolormesh(x_i, y_j, bs_vol, cmap='jet')
# fig.colorbar(cax, ax=ax)
ax.streamplot(x_i, y_j, bs_x, bs_y,  linewidth=0.8, density=0.7, broken_streamlines=False)
ax.set_aspect(3)
ax.set_xlim(0, 7.0)  
ax.set_ylim(0, 0.8) 
ax.set_title('B field')
ax.set_xlabel('x')
ax.set_ylabel('y')
fig.colorbar(cax,shrink=0.8)

これで直行グリッドデータが得られました!!!!!!!

まとめ

FEMMは点データだったので2次のスプラインを用いて直行グリッドデータに変換しました。FEMMの時のスケールが小さい方が精度がいいのでその辺注意ですね。あとは、データのコピーが最もだるいのでいいやり方を教えてください...

1.FEMMの特徴としたいこと

2.FEMM解析結果 .ans ファイルの中身

3.データを読み込む

4.データの加工と描画

5.点のデータを直行グリッドにする

磁場を求める

まとめ

Discussion