Pythonを使って二次元分布を作る(cosの分布)
数値シミュレーションで粒子位置の初期分布や注入位置の分布を作る必要が生じたので、その過程をまとめてみました。x方向とy方向が影響を及ぼし合う場合は難しいと思ったのでそれぞれ、独立した分布としてまずは作ってみます。今回はPyhonでやってきます。
1.まずは簡単な1次元分布
それぞれx方向、y方向影響しない分布にすることにしたので、1次元(x方向)でできれば同じことをy方向でやればいいってことなので、まずは、1次元をやりますー。
1.1.ランダムの描画
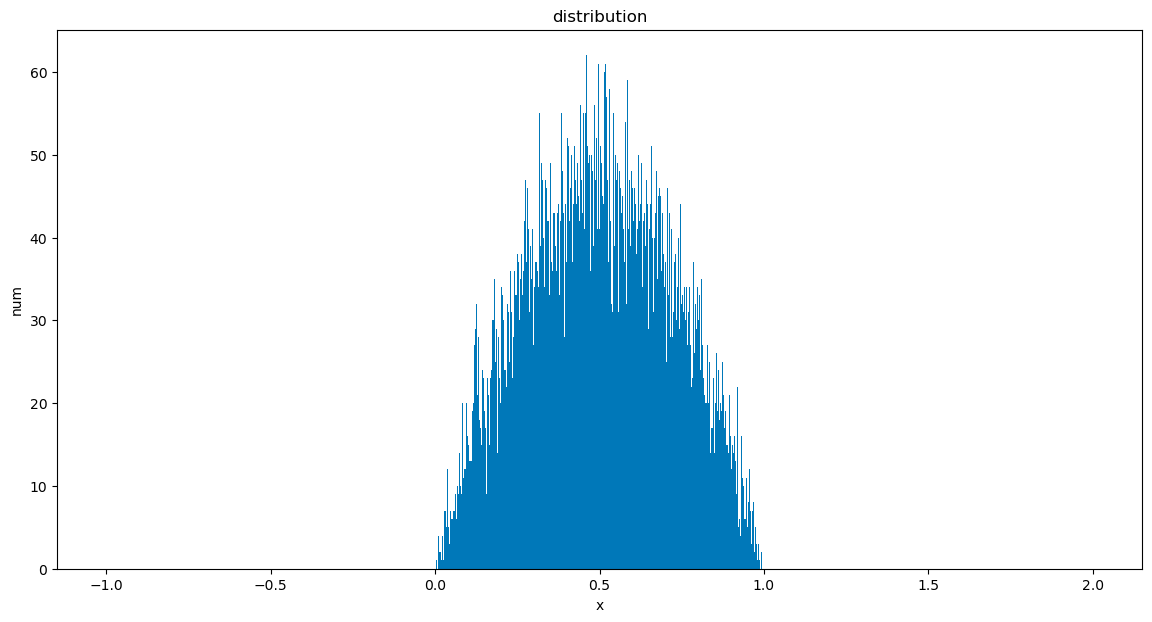
まずは、デフォルトの乱数を描画します。10000個の乱数を生成して描画してみます。
## 使うライブラリ ##
import numpy as np
import matplotlib.pyplot as plt
## 乱数生成 ##
x = np.random.rand(10000)
## ヒストグラムを描画 ##
fig = plt.figure(figsize=(14,7))
plt.hist(x, bins=1000, range=(-1,2)) # binsはビンの数
plt.title('distribution')
plt.xlabel('x')
plt.ylabel('num')
plt.show()

デフォルトは0~1の値ですね
1.2.cosの分布の描画
0~1のランダムの値をcosの分布にするにはどうしたらいいだろう...
まずは想定する分布を0~1までのこんな分布としてやってみます。

0~1の一様な分布では均等に個数が生まれるが、cosの分布は0や1付近はすごく少なくて、0.5付近が多い感じ。
つまり、生成する値が関数でいう
と考えました。
ちょっと変数を入れ替えて最初のランダムな値を
実装してみまーす。
まとめると、
1. 0~1のデフォルト乱数を-1~1に変換
2.
3.
です。やってきまーす。
## 使うライブラリ ##
import numpy as np
import matplotlib.pyplot as plt
## 乱数生成 ##
x = np.random.rand(10000)
## [0,1]を[-1,1]に変換 ##
x = 1 - 2*x
## [0,1]のcos分布に変換 ##
x = np.arccos(x)/np.pi
## ヒストグラムを描画 ##
fig = plt.figure(figsize=(14,7))
plt.hist(x, bins=1000, range=(-1,2)) # binsはビンの数
plt.title('distribution')
plt.xlabel('x')
plt.ylabel('num')
plt.show()
できたできた。これをスライドさせれば任意の位置でcos分布を作れる!!!
## 使うライブラリ ##
import numpy as np
import matplotlib.pyplot as plt
## 乱数生成 ##
x = np.random.rand(10000)
## [0,1]を[-1,1]に変換 ##
x = 1 - 2*x
## [0,1]のcos分布に変換 ##
x = np.arccos(x)/np.pi
## 任意の位置に作る ##
x_min = 2
x_max = 5
x = (x_max-x_min)*x + x_min
## ヒストグラムを描画 ##
fig = plt.figure(figsize=(14,7))
plt.hist(x, bins=1000, range=(0,6)) # binsはビンの数
plt.title('distribution')
plt.xlabel('x')
plt.ylabel('num')
plt.show()

おけ!!完璧
1.3.cosの山を二つ任意の場所に作りたい
もう少し複雑にしてみたいということで2つの山を任意の場所に作ってみます。色々考えたのですが、分岐を使って分けてみようと思います。最初の乱数で0.5を閾値として0.5より小さい方の分布と大きいほの分布でスライドさせる値を変えて作ります。
import numpy as np
import matplotlib.pyplot as plt
# 個数
num = 10000
# 乱数生成
x = np.random.rand(num)
flag = np.random.rand(num)
# 位置の設定
x_min = np.where(flag <= 0.5, 2, 5)
x_max = np.where(flag <= 0.5, 4, 7)
# [0,1]を[-1,1]に変換し、その後の計算
x = 1 - 2 * x
x = np.arccos(x) / np.pi
x = (x_max - x_min) * x + x_min
# ヒストグラムを描画
fig = plt.figure(figsize=(14,7))
plt.hist(x, bins=1000, range=(0,8)) # binsはビンの数
plt.title('distribution')
plt.xlabel('x')
plt.ylabel('num')
plt.show()

いい感じです!!!
これは、フーリエ変換の容量でたくさん分岐とその割合を変えていけば複雑な分布を作れるのではないか????
いつかやってみたいですね。
2. 二次元の分布にしてみましょう!!!
想定はx方向には1つのコブの分布y方向には2つコブの分布を作ってみたいと思います。
ポイントはxとyで同じランダムの値を使ってはならないところです。xyの2つの関係が生じることになります。(直線)
(ってことはもっと複雑なxyが関係し合う分布も作れるのでは...????)
これもいつか試してみよう...
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
# 個数
num = 10000000
# 乱数生成
r_x = np.random.rand(num)
r_y = np.random.rand(num)
flag = np.random.rand(num)
# x位置の設定
x_min = 1.5
x_max = 2.5
# y位置の設定
y_min = np.where(flag <= 0.5, 0, 0.36)
y_max = np.where(flag <= 0.5, 0.44, 0.8)
# [0,1]を[-1,1]に変換し、その後の計算
r_x = 1 - 2 * r_x
r_x = np.arccos(r_x) / np.pi
r_y = 1 - 2 * r_y
r_y = np.arccos(r_y) / np.pi
x = (x_max - x_min) * r_x + x_min
y = (y_max - y_min) * r_y + y_min
# ヒストグラムを描画
fig = plt.figure(figsize=(14,7))
plt.hist2d(x,y, bins=1000, range=[(0, 7), (0, 0.8)],cmap=cm.jet) # binsはビンの数
plt.title('distribution')
plt.xlabel('x')
plt.ylabel('num')
plt.show()

なかなか面白そうな分布が出来ました。2次元のヒストグラムはhist2dというものがありました!!!!
まとめ
-
\arccos - 二次元の場合ランダムの値の扱いに注意。
ぐらいですかね。
0~1の材料ができれば自由自在!!!! もっと複雑な分布を作ってみたいですね。(できるだけ実験を模擬したい!!!)
Discussion