CGソフトごとの行列の違い
CGソフトによって、同じ変換を表現する行列演算の見た目が異なる。
例えば、座標(1,2,3)の点をY軸方向に5移動する変換は、以下のようになる。
・MayaやHoudini
\begin{bmatrix}
1 &2 &3
\end{bmatrix}
\begin{bmatrix}
1 &0 &0 &0\\
0 &1 &0 &0\\
0 &0 &1 &0\\
0 &5 &0 &1
\end{bmatrix}
・BlenderやBifrost
\begin{bmatrix}
1 &0 &0 &0\\
0 &1 &0 &5\\
0 &0 &1 &0\\
0 &0 &0 &1
\end{bmatrix}
\begin{bmatrix}
1\\
2\\
3
\end{bmatrix}
| Mayaの例 |
Bifrostの例 |
 |
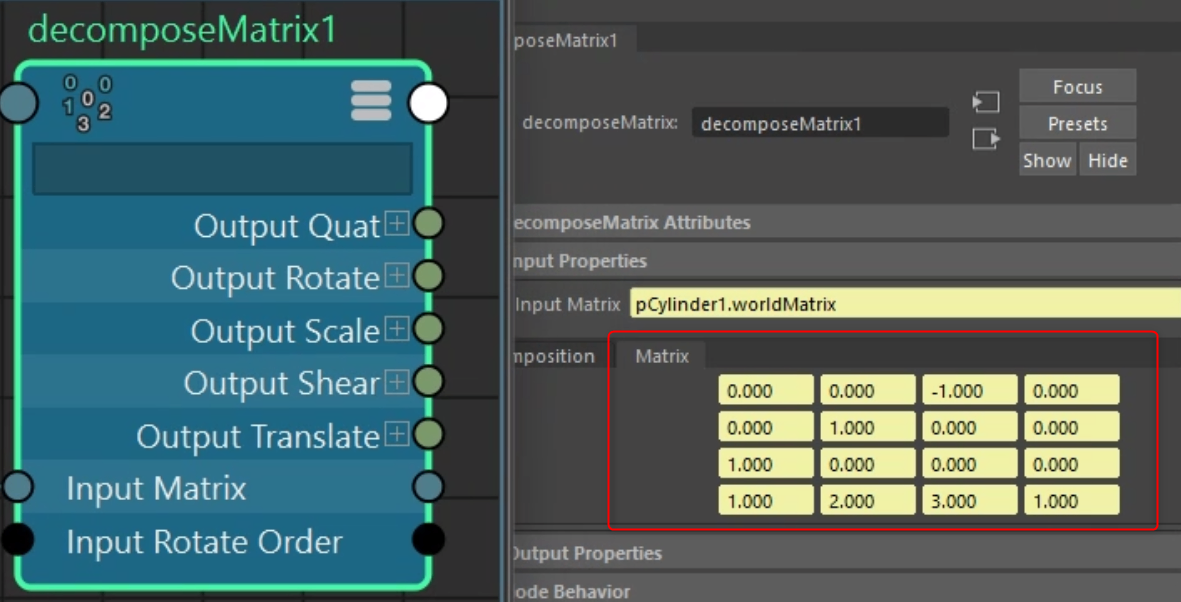 |
上の画像の行列はいずれも同じ変換を表している。
行優先(row-major)と列優先(column-major)
行優先、列優先と言ったとき、データ保持形式の違いを指す場合と数学的表現の違いを指す場合があるが、ここでは、主に数学的表現について扱う。
ソフトや書籍によって行優先か列優先かが異なっており、初心者の混乱の原因となっている。
行優先(列優先)の資料の計算を列優先(行優先)のソフトで再現する場合は、行列を転置し合成順を逆にして読み替える必要がある。
しかし、使用するソフトが行優先か列優先か分かっていれば、簡単に読み替えることができる。
行優先/列優先のソフトや書籍の例
行優先のソフトや書籍の例
Maya
Houdini
DirectX
『3Dグラフィックスのための数学入門』
『実例で学ぶゲーム3D数学』
列優先のソフトや書籍の例
Bifrost
Blender
OpenGL
Unity(shaderは行優先オーダーだが、列ベクトル前提で計算を行う)
『ゲーム開発のための数学・物理学入門』
『プログラミングのための線形代数』
『線形代数入門』(斎藤正彦)
行優先と列優先の違い
ベクトル
ベクトルは、行優先の際は行ベクトル、列優先の際は列ベクトルとして表される。
行優先:
\begin{bmatrix}
a_1 &a_2 &a_3
\end{bmatrix}
\qquad 列優先:
\begin{bmatrix}
a_1\\
a_2\\
a_3
\end{bmatrix}
合成順
合成変換は、行優先ではベクトルの右側、列優先ではベクトルの左側に順にかけていく。
行優先:
V' = VM_1M_2M_3
\qquad 列優先:
V' = M_3M_2M_1V\\
\scriptsize{V':変換後のベクトル M:変換行列 V: 変換前のベクトル}
行列
行優先では、1、2,3行目がX軸Y軸Z軸を表し、4行目が移動を表す。
列優先では、1、2,3列目がX軸Y軸Z軸を表し、4列目が移動を表す。
行優先:\begin{bmatrix}
X_x &X_y &X_z &0\\
Y_x &Y_y &Y_z &0\\
Z_x &Z_y &Z_Z &0\\
T_x &T_y &T_z &1
\end{bmatrix}
\qquad 列優先:
\begin{bmatrix}
X_x &Y_x &Z_x &T_x\\
X_y &Y_y &Z_y &T_y\\
X_z &Y_z &Z_Z &T_z\\
0 & 0& 0&1
\end{bmatrix}
読み替え
行優先と列優先を読み替えるには、単に式全体を転置すればいい。
行優先を列優先に変換する場合以下のようになる。
VM_1M_2M_3 → (VM_1M_2M_3)^T → M_3^TM_2^TM_1^TV^T
\begin{align*}
&例:
(\begin{bmatrix}
1 &2 &3
\end{bmatrix}
\begin{bmatrix}
1 &0 &0 &0\\
0 &1 &0 &0\\
0 &0 &1 &0\\
0 &-5 &0 &1
\end{bmatrix}
\begin{bmatrix}
2 &0 &0 &0\\
0 &2 &0 &0\\
0 &0 &2 &0\\
0 &0 &0 &1
\end{bmatrix}
\begin{bmatrix}
1 &0 &0 &0\\
0 &1 &0 &0\\
0 &0 &1 &0\\
0 &5 &0 &1
\end{bmatrix})^T \\&=
\begin{bmatrix}
1 &0 &0 &0\\
0 &1 &0 &5\\
0 &0 &1 &0\\
0 &0 &0 &1
\end{bmatrix})
\begin{bmatrix}
2 &0 &0 &0\\
0 &2 &0 &0\\
0 &0 &2 &0\\
0 &0 &0 &1
\end{bmatrix}
\begin{bmatrix}
1 &0 &0 &0\\
0 &1 &0 &-5\\
0 &0 &1 &0\\
0 &0 &0 &1
\end{bmatrix}
\begin{bmatrix}
1\\
2\\
3
\end{bmatrix}
\end{align*}
Bifrostでの例
Bifrostは列優先なので、後ろ、つまりポートの下から順に行列をかける。

まとめ
・ソフトや書籍によって、行列演算の数式の見た目が異なる。
・移動値が4行目か4列目か、ベクトルが行か列か、等の特徴から見分けることができる。(※CGで変換に使用する行ベクトルは1x4であるため、4x4行列は右からしかかけられない。)
・行優先と列優先を読み替えるには式全体を転置すればいい。



Discussion