[前編] 機械学習超入門視聴メモ
ta.toshioudemyの講座メモ用スクラップ
ta.toshio3 線形回帰
ta.toshio4 正規方程式
行列復習
正規方程式導出
⭐⭐
ta.toshio5 特徴量スケーリング
feature scaling
標準化（standardize）
平均を0、分散を1にすること -> z得点
各値から平均を引き、標準偏差で割る
sklearn.preprocessing.StandardScaler
s = StandardScaler()
s.fit(X)
.transform(X)
正規化（normalization）
値の範囲を0 - 1にリスケールする処理
x - xmin / xmax - xmin
xminは0にxmaxは1になる
sklearn.preprocessing.MinMaxScaler
s = MinMaxScaler())
s.fit(X)
.transform(X)
標準化 vs 正規化
注意点
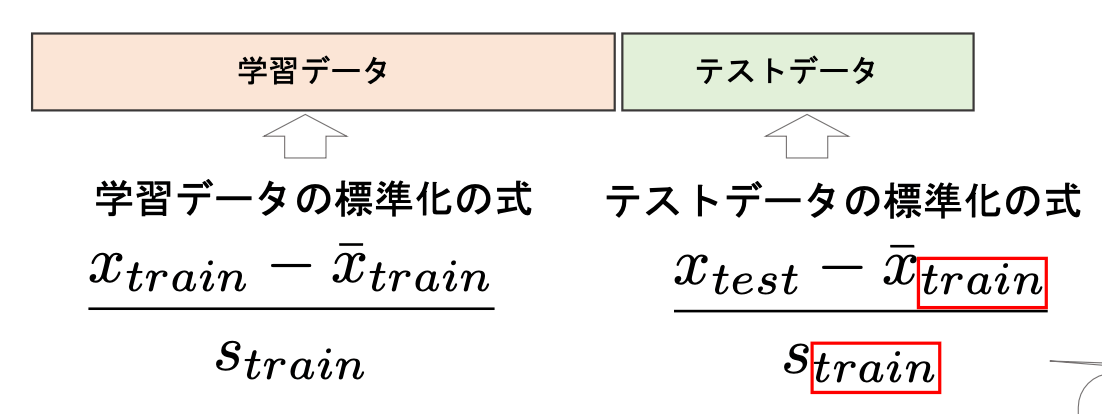
特徴量スケーリング等でテストデータを処理する場合は，学習データのパラメ ータを使用することに注意
ta.toshio6 整形回帰の解釈
標準誤差: 推定量の標準偏差
線形回帰の係数の統計的仮説検定（t検定）
帰無仮説と対立仮説を立てる
t分布
p値
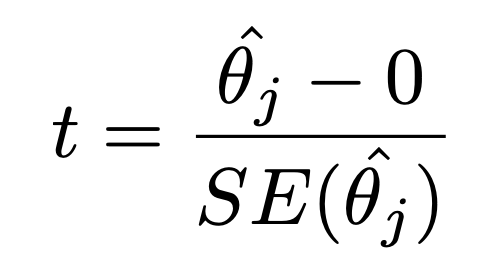
参考
線形回帰の係数の有意差の確認
statsmodels.api.OLS
バイアス項用の列を追加
statsmodels.api.add_constatnt(X)
係数の仮説検定（F検定）
すくなくとも係数の一つは0ではないを検定によって確認
係数のF検定の検定料
- 帰無仮説のRSSと対立仮説のRSSの差の比率を考える
- それぞれのRSSをそれぞれの自由度dfで割る
TSS: 偏差の二乗和 : Total Sum of Squares
RSS: 残差の二乗和 : Residual Sum of Squares
df0 = m- 1 : 帰無仮説が正しいとした時の自由度
dfα = m - n - 1 : 対立仮説が正しいとした時の自由度
ta.toshio7 質的変数の特徴量
one-hotエンコーディング
ダミー変数トラップ
2つの特徴量間に完全な相関ができてしまう
-> 多重共線性（multicollinearity）
ダミー変数に対する標準化はしても良いが，やらないことが多い
ta.toshio8 汎化性能と過学習
汎化性能: 「未知のデータ」に対して正しく予測できる性能
学習に使うデータ(学習データ)と評価に使うデータ(テストデータ)を区別する。今回の講座では以下の3つのやり方を紹介
hold-out
LOOCV
k-FoldCV
特徴量スケーリング復習
特徴量スケーリング等でテストデータを処理する場合は，学習データのパラメ ータを使用することに注意
hold-out
ランダムに学習データとテストデータに分割する
7:3や5:5に分けるのが一般的
全てのデータを学習に使えないのが難点
hold-out
sklearn.model_selecLon.train_test_split
LOOCV
Leave-One-Out Cross Valiation
一つのデータだけテストデータとし，残りのデータで学習し全てのデータがテストデータになるように繰り返し平均を取る
交差検証（Cross Validation）
LOO
l = sklearn.model_selecLon.LeaveOneOut()
l.split(X)
Cross Validation
sklearn.model_selecLon.cross_val_score
k-Fold CV
データをk個に分割して交差検証を行う(よく使われるのはk=5やk=10)
k-Fold CV
sklearn.model_selecLon.KFold
Repeated k-Fold CV
sklearn.model_selecLon.RepeatedKFold
Pipeline(k-FoldCV + 標準化)
sklearn.pipeline.Pipeline
⭐
Bias-Variance Tradeoff
削減可能な誤差はBiasとVarianceに分解することが可能
参考
LOOCV vs k-Fold CV
ta.toshio9 回帰モデルの精度指標
MSE (Mean Squared Error)
RMSE (Root Mean Squared Error)
MAE (Mean Aboslute Error)
R-Squared (𝑅!:決定係数)
MSEおよびRMSE
sklearn.metrics.mean_squared_error
squared引数にFalseを渡すとRMSEを返す
MAE
sklearn.metrics.mean_absolute_error
R-Squared（決定係数）
統計学では決定係数とも呼ばれる
データに対して回帰の当てはまりの良さを0~1で表す
特徴量がどれだけ目的変数の値を説明(決定)しているのかを表す
𝑦の分散は𝑥によってどれだけ説明(決定)されるかを表す指標
⭐
sklearn.metrics.r2_score
adjusted R-squared（調整済みR²）
ta.toshio10 非線形回帰
- 多項式特徴量
- kNN
多項式特徴量（Polynomial Features）
⭐
sklearn.preprocessing.PolynomialFeatures
kNN（k Nearest Neighbor: k最近傍法）
分類でよく使われるが，回帰にも使える(kNN回帰)
数式モデルを使わないノンパラメトリックな手法
学習データで最もX距離が近いk個のデータの平均を予測値とする
kNNのような距離ベースのアルゴリズムでは特徴量スケーリングが必要
距離の考え方
ユークリッド距離
マンハッタン距離
sklearn.neighbors.KNeighborsRegressor
ta.toshio11 正則化項
線形回帰の精度と解釈性をさらに向上させる
最小二乗法の損失関数の式に，正則化項と呼ばれるペナルティを課す項をつける
パラメータ𝜃が大きくなると損失が増えるようにする⇨パラメータ𝜃が大きくならないようにする
一般の線形回帰は，特徴量数が多いとlow bias high varianceになりやすい
varianceを下げる必要がある⇨正則化項を使う
Ridge
L2ノルムの正則化項を使用
𝜆を大きくするにつれ各特徴量の係数の絶対値は小さくなる(一時的には大きくなる場合も 特徴量同士のスケールが影響するので事前に特徴量スケーリングが必要
学習後，全ての特徴量の係数が残ることに注意
Lasso
L1ノルムの正則化項を使用
𝜆を大きくするにつれ各特徴量の係数の絶対値が小さくなり，やがて0になる
特徴量同士のスケールが影響するので事前に特徴量スケーリングが必要
学習後，一部(or全て)の特徴量の係数が0になることを期待する
-> Lassoは特徴量選択を自動で行うアルゴリズム
Ridge、Lassoのもう一つの式
⭐