Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎

読書メモ

1章

答えようとしている問いは何か？集めたデータでその問いに答えられるか、
問題を大きく捉えると、機械学習のアルゴリズムや手法はある問題を解く大きな過程のごく一部にすぎない、...多大な時間を費やして...正しい問題を問いていなかったことがわかる、という例は数多い

1.7

クラス分類
クラス
ラベル

クラス

データセットの中のすべてのアイリスは3つのクラスのうちの1つに属するので、この問題は4クラス分類問題となる

ラベル

特定のデータポイントに属する種類をラベルと呼ぶ

アイリスデータでは花の種類

モデルが汎化（generalize）できている:
新たなデータに対してもうまく予測機能する

訓練データ = 訓練セット
テストデータ = テストセット = ホールドアウトセット

1.7.3 最初にすべきこと：データをよく観察する

データを検査する最良の方法は、可視化である。その方法の1つが散布図である。...2つまでの特徴量しか同時にはプロットできない。したがって3つを超える特徴量を持つデータセットを...する方法の1つがペアプロット

from sklearn.datasets import load_iris
iris_dataset = load_iris()

# create dataframe from data in X_train
# label the columns using the strings in iris_dataset.feature_names
iris_dataframe = pd.DataFrame(X_train, columns=iris_dataset.feature_names)
# create a scatter matrix from the dataframe, color by y_train
pd.plotting.scatter_matrix(iris_dataframe, c=y_train, figsize=(15, 15),
                           marker='o', hist_kwds={'bins': 20}, s=60,
                           alpha=.8, cmap=mglearn.cm3)

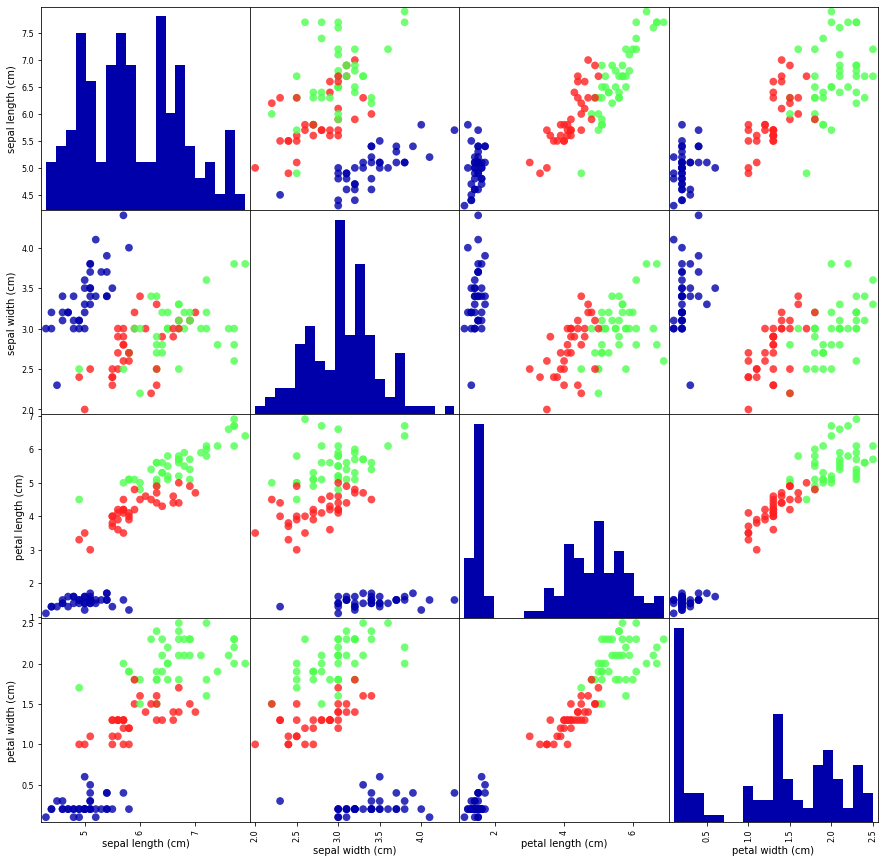
petal widthとpetal lengthの測定結果で比較的よく分離していることがわかる。これは、うまく分離できるように機械学習モデルを訓練することができる可能性が高いことを意味する

1.7.5 予測を行う

TIPS

（入力データを）2次元のNumPy配列にしていることに注意しよう。これはscikit-learnが常に入力が2次元NumPy配列であることを前提しているからだ。

np.array([[1, 2, 3, 4]]).shape
(1, 4)
np.array([1, 2, 3, 4]).shape
(4,)

1.8

クラス分類では、分類結果となる品種はクラスと呼ばれ、個々のアイリス（花)の品種はラベルと呼ばれる

2章 教師あり学習

2.1 クラス分類と回帰

クラス分類（classsificatoin）
回帰（regression）

クラス分類の目的は、あらじめ定められた選択肢の中からクラスラベルを予測することである

2クラス分類（binary classification）
多クラス分類（multiclass classificatoni）

2クラス分類は、答えがyes/noになる問いに答えるようなものと考えればよい。...「このメールはスパムか」というyes/no問題が問われている。一方アイリスの例は多クラス分類問題だ。

2クラス分類では、しばしば一方のクラスを陽性（positive）クラス、もう一方を陰性（negative）クラスと呼ぶ。ここで言う「陽性」という言葉は、そちらの方が良いという意味ではなく、単に解析の対象であることを意味する。例えば、SPAMフィルタの場合、SPAMクラスのほうが「陽性」であってもよい。

回帰タスクの場合、目的は連続値の予測だ。

2.2 汎化、過剰適合、適合不足

過剰適合（overfitting） = 過学習 <-> 適合不足（underfitting）

スイートスポットを狙う

2.2.1 モデルの複雑さとデータセットの大きさ

データセットに含まれるデータポイントがバリエーションに富んでいれば、過剰適合を起こすことなく、より複雑なモデルを利用できる。...教師あり学習タスクにおいては、より多くのデータを用いると、驚くほどうまくいくとがある。...モデルを弄り回すよりもデータ量をしたほうがよい場合も多い。

2.3 教師あり機械学習アルゴリズム

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

cancer.target_names
-> array(['malignant', 'benign'], dtype='<U9')

cancer.target[:30]
-> array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
       0, 0, 0, 0, 0, 0, 0, 0])

np.bincount(cancer.target)
-> array([212, 357])

print("Sample counts per class:\n",
      {n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))})
Sample counts per class:
->  {'malignant': 212, 'benign': 357}

2.3.2 k-最近傍法

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)
...

2.3.2.2 k-近傍回帰

# instantiate the model and set the number of neighbors to consider to 3
reg = KNeighborsRegressor(n_neighbors=3)

scoreメソッドを用いて評価することもできる。...R²スコアを返す。R²スコアは決定係数（coefficent of determination）と呼ばれる

多数の特徴量（数百以上）を持つデータセットではうまく機能ｓない
ほとんどの特徴量が多くの場合0となるような（疎なデータセット:sparse dataset）データセットでは特に性能が悪い

2.3.3 線形モデル

2.3.3.1 線形モデルによる回帰

回帰問題では、線形モデルによる一般的な予測式は以下のようになる

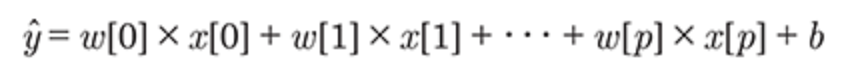
ここでx[0]からx[p]は、ある1データポイントの特徴量（この例では特徴量の数はp+1）を示し、xとbは学習されたモデルのパラメータであり、yハットはモデルからの予測である。特徴量が1つしかないデータセットであれば次のようになる

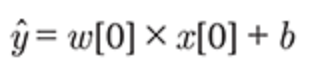
この式が直線を表していることがわかるだろう。w[0]は傾きを、bはy切片を意味する。

回帰における線形モデルは、単一の特徴量に対しては予測が直線になる回帰モデルとして特徴つけられる。特徴量が2つなら予測は平面に、高次元において（つまり特徴量が多いとき）は予測は超平面になる

線形モデルを用いた会期にはさまざまなアルゴリズムがある。これらのモデルの相違点は、パラメータwとbを訓練データから学習する方法とモデルの複雑さを制御する方法にある

2.3.3.2 線形回帰（通常最小二乗法）

訓練データにおいて、予測と真の回帰ターゲットyとの平均二乗誤差（mean squared error）が最小になるように、パラメータwとbを求める

from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

lr = LinearRegression().fit(X_train, y_train)

print("lr.coef_:", lr.coef_) # 「傾き」を表さすパラメータwは、重み、もしくは係数(coefficient)と呼ばれ、coef_に格納される
print("lr.intercept_:", lr.intercept_)  # オフセットもしくは切片（intercept, b, bias）はintercept_に格納される

2.3.3.3 リッジ回帰

リッジ回帰は線形モデルによる回帰の１つである。予測に用いられる式は、正常最小二乗法のものと同じである。しかし、リッジ回帰では、係数（w）を、訓練データに対する予測だけでなく、他の制約に対しても最適化する。ここでは、係数の絶対値の大きさを可能な限り小さくしたい。つまり、wの要素をなるべく0に近くしたいのだ。直感的には、予測をうまく行いつつ、個々の特徴量が出力に与える影響をなるべく小さくしたい（つまり傾きを小さくしたい）。この制約条件は、正則化（regularization）の一例である。正則化とは、過剰適合を防ぐために明示的にモデルを制約することである。リッジ回帰で用いられている正則化は、L2正則化と呼ばれる。
数学的にいうと、Ridgeでは、係数のL2ノルム、つまりwのユークリッド長に対してペナルティを与える。

Rdigeモデルでは、モデルの簡潔さ（0に近い係数の数）と、訓練セットに対する性能がトレードオフの関係になる。このどちらに重きを置くかは、ユーザーがalphaパラメータを用いて指定するとができる。
alphaを増やすと、係数はより0に近くなり、訓練セットに対する性能は低下するが、汎化はそちらのほうがよいかもしれない。

十分な訓練データがある場合には、正則化はあまり重要ではなくなるということである。十分なデータがあるならばリッジ回帰と線形回帰は同じ性能を示す。

Lasso

リッジ会期と同様に、Lassoも係数が0になるように制約をかけるのだが、かけかたが少し違い、こちらはL1正則化と呼ばれる。

Lassoでは係数ベクトルのL1ノルム、すなわち係数ベクトルの絶対値の和にペナルティを与える。

L1正則化の結果、Lassoにおいては、いくつかの係数が完全に0になる。これは、モデルにおいていくつかの特徴量が完全に無視されるということになる。自動的に特徴量を選択していると考えても良い。いくつかの係数が0になると、モデルを解釈しやすくなり、どの特徴量が重要なのかが明らかになる。

実際に使う場合には、この２つのリッジ回帰をまず試してみるとよいだろう、しかし、特徴量がたくさんあって、そのうち重要なものはわずかしかないことが予測されるのであれば、Lassoのほうが向いているだろう。

sceikit-learnにはLassoとRidgeのペナルティを組み合わせたElasticNetクラスがある。...L1正則化のパラメータとL2正則化のパラメータの2つを調整するというコストがかかる

2.3.3.5 クラス分類のための線形モデル

線形モデルはクラス分類にも多様されている。
特徴量の重み付き和を単に返すのではなく、予測された値が0を超えるかどうかで分割している。
線形の2クラス分類器は、2つのクラスを直線や平面や超平面で分割するということだ。

線形モデルを学習するにはさまざまなアルゴリズムがある。これらのアルゴリズムは以下の2点で区別される。

• 係数と切片の特定の組み合わせと訓練データの適合度を測る尺度
• 正規化を行うか。行うならどの方法を使うか

ロジスティック回帰（Logistic regression）
線形サポートベクタマシン（linear support vector machines）

LogisticRegressionとLinearSVC（サポートベクタークラス分類器: support vector classifier）における正則化の強度を決定するトレードオフパラメータはcと呼ばれ、cが大きくなると正則化は弱くなる。つまりパラメータcを大きくすると、訓練データに対しての適合度をあげようとするが、パラメータcを小さくすると係数ベクトル（w）を0に近づけることを重視するようになる。
cの影響にはもう１つ面白い側面がある。小さいcを用いると、データポイントの「大多数」に対して適合しようとするが、大きいcを用いると、個々のデータポイントを正確にクラス分類することを重視するようになる。

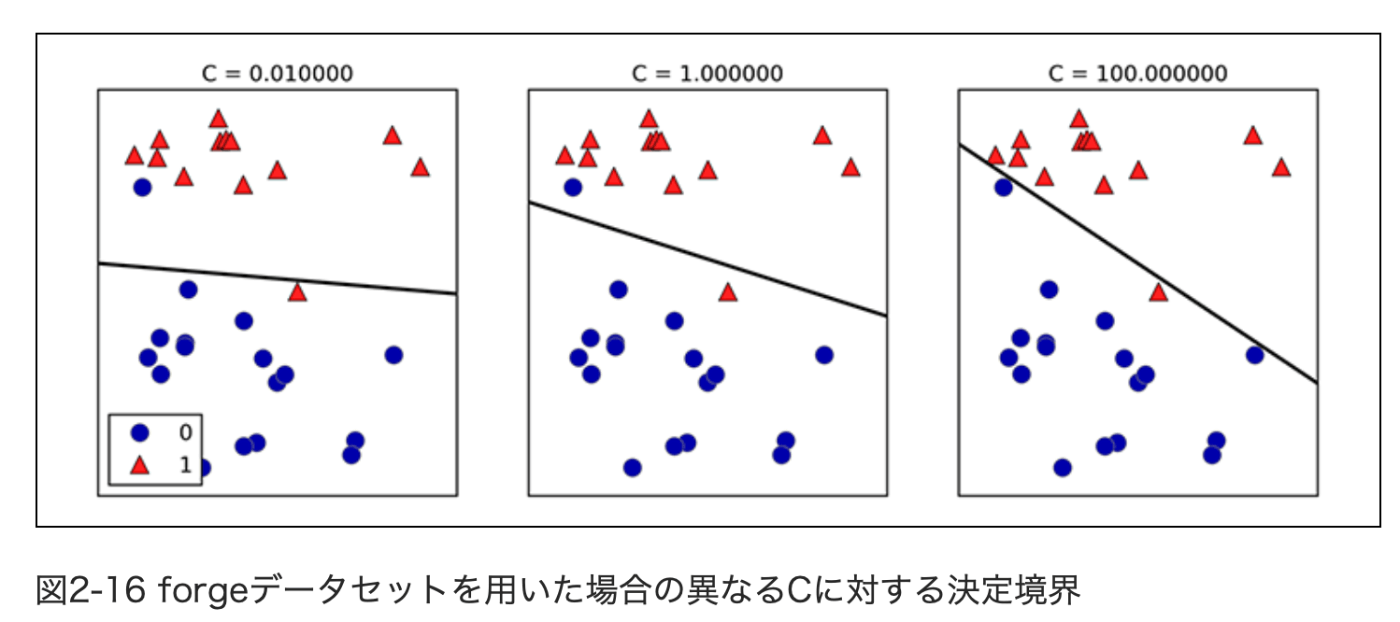
出所: 同書籍

2.3.3.6 線形モデルによる多クラス分類

多くの線形クラス分類モデルは、2クラス分類にしか適用できず、自然に多クラスの場合に拡張できるものではない（ロジスティック回帰は例外）
2クラス分類アルゴリズムを多クラス分類アルゴリズムに拡張する一般的な手法として1対その他（one-vs.-rest）アプローチがある。

• -(line * coef[0] + intercept) / coef[1]
• グラフの中央の三角形
• f「クラス分類式の値が一番大きいクラス」
  の部分がもやった

2.3.3.7 利点、欠点、パラメータ

回帰モデルではalpha、LogisticRegressionとLinearSVCではcと呼ばれる正則化パラメータ
alphaが大きい場合、cが小さい場合は単純なモデルに対応する

cが大きい場合は過学習気味、cが小さい場合（alphaが大きい）は正則化、係数ベクトルを0に近づける

L1正則化を使うか、L2正則化を使うか

サンプル点が10万点、100万点もあるようなデータに対しては、LogisticRegressionとRidgeにsolver='sag'オプションを使うことを検討したほうがよいだろう。...デフォルトの場合よりも高速な場合がある。

2.3.4 ナイーブベイズクラス分類機

GaussianNBは任意の連続値データに
BeronulliNBは2値データ
MultinomialNBはカウントデータ
カウントデータとは、例えば文中に出てくる単語の出現数などの、個々の特徴量が何らかの整数カウントを表現しているデータ

2.3.5 決定木

2.3.5.1 決定木の構築

2.3.5.2 決定木の複雑さの制御

過剰適合を防ぐには2つの戦略がある。
構築過程で木の生成を早めに止める事前枝刈り（pre-pruning）
一度木を構築してから、情報量の少ないノードを削除する事後枝刈り（post-pruning）（ただの枝刈り: pruningとも呼ばれる）

scikit-learnでは決定木はDecisionTreeRegressorクラスとDecisionTreeClassfierクラス

木が完全に訓練データに適合する前に木の成長を止めてみよう。1つの方法は、木がある深さに達したらそこで止めるという方法だ。ここではmax_depth=4

from sklearn.tree import DecisionTreeClassifier

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)

print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))
Accuracy on training set: 0.988
Accuracy on test set: 0.951

2.3.5.3 決定木の解析

treeモジュールのexport_graphviz関数を使って木を可視化することができる。

2.3.5.4 決定木の特徴量の重要性

決定木の挙動を要約する特性値を見てみよう。要約に最も使われるのは、特徴量の重要度（feature importance）と呼ばれる、決定木が行う判断にとって、個々の特徴量がどの程度重要かを示す割合である。それぞれの特徴量に対する0と1の間の数で、0は「まったく使われていない」1は「完全にターゲットを予想できる」を意味する。特徴量の重要度の和は常に1になる。

すべての決定木による回帰モデルは、外挿（extrapolate）ができない。つまり訓練データのレンジの外側に対しては予測できない

2.3.5.5 長所、短所、パラメータ

過剰適合を防ぐには事前枝刈り戦略を指定するmax_depth、max_leaf_nodes、min_samples_leafのどれか1つを選ぶだけで十分だ

決定木の最大の問題点は、事前枝刈りを行ったとしても、過剰適合しやすく、汎化性能が低い...決定木は単体で使うのではなく、次に見るアンサンブル法が用いられる

2.3.6 決定木のアンサンブル法

アンサンブル法（Ensembles）とは、複数の機械学習モデルを組み合わせることで、より強力なモデルを構築する手法だ。...さまざまなデータセットに対するクラス分類や回帰に関して有効であることがわかっているアンサンブル法が２つある。ランダムフォレストと勾配ブースト決定木である。

2.3.6.1 ランダムフォレスト

決定木の最大の問題点は訓練データに対して過剰適合してしまうことにある。ランダムフォレストはこの問題に対応する方法の１つ
ランダムフォレストとは、要するに少しずつ異なる決定木をたくさん集めたものだ。...それぞれ異なった方向に過剰適合した決定木をたくさん作れば、その平均をとることで過剰適合の度合いを減らすことができる。

ブートストラップサンプル

説明、書籍参照

ランダムフォレストは、テキストデータなどの、非常に高次元で疎なデータに対してはうまく機能しない傾向にある

ちょうすべき重要なパラメータは、n_estimators、mas_featuresと、max_depthなどの事前枝刈りパラメータである。n_estimatorsは大きければ大きい方がよい。より多くの決定機の平均を取ると、過剰適合が低減されアンサンブルが頑健になるからだ。しかし...メモリの量も訓練にかかる時間も増大する。「時間とメモリのある限り大きくする」ということになる
上に述べたように（書籍参照）max_featuresは個々の決定木の乱数性を決定するとともに、max_featuresが小さくなると過剰適合が低減する。一般にはデフォルト値を使うと良いだろう。クラス分類についてはmax_features=sqrt(n_features)、回帰についてはmax_features=n_featuresとなっている。

2.3.6.2 勾配ブースティング回帰木（勾配ブースティングマシン）

勾配ブースティング回帰木は、複数の決定木を組み合わせてより強力なモデルを構築するもう１つのアンサンブル手法である。
名前に「回帰」とついているが、このモデルは回帰にもクラス分類にも利用できる。

勾配ブースティングでは、1つ前の決定木の誤りを次の決定木が修正するようにして、決定木を順番に作っていく。デフォルでは、勾配ブースティング回帰木には乱数性はない。
勾配ブースティング回帰木では、深さ１から５ぐらいの非常に浅い決定木が用いられる。
勾配ブースティングのポイントは、浅い決定木のような、簡単なモデル（このコンテクストでは弱学習機（weak learner）と呼ぶ）を多数組み合わせることにある。それぞれの決定木はデータの一部に対してしか良い予測を行えないので、決定木を繰り返し追加していくことで、性能を向上させるのだ。

勾配ブースティング回帰木には、事前枝刈りとアンサンブルに用いる決定木の数を設定するパラメータの他に、learnng_rate（学習率）という重要なパラメータがある。これは、個々の決定木が、それまでの決定木の過ちをどれくらい強く補正しようとするかを制御するパラメータである。

続きの解説は書籍参照

他の決定木ベースのモデルと同じように、特徴量のスケール変換をする必要はなく、2値特徴量と連続特徴量が混在してもうまく機能する。また、はやり高次元の疎なデータに対してはあまりうまく機能しない

パラメータの機微は書籍参照

2.3.7 カーネル法を用いたサポートベクタマシン

カーネル法を用いたサポートベクタマシン詳細が知りたければFriedmanの『The Elements of Statistical Learning（http://statweb.stanford.edu/~tibs/ElemStatLearn/、邦題『統計的学習の基礎』共立出版）の12章を参照してほしい

2.3.7.1 線形モデルと非線形特徴

低次元における線形モデルは非常に制約が強い。直線や超平面が柔軟性を制限するからだ。線形モデルを柔軟にする方法の1つが、特徴量を追加することだ。例えば、入力特徴量の交互作用（積）や多項式項を加えることが考えられる。

2.3.7.2 カーネルトリック

2.3.7.1でわかるのは、非線形の特徴量をデータ表現に加えることで、線形モデルがはるかに強力にあるということだ。しかし、実際どの特徴量を加えたらよいかわからない。...高次元空間でのクラス分類器を学習させる巧妙な数学的トリックがある。これがカーネルトリック（kernel trick）と呼ばれるもので、拡張された特徴表現上でのデータポイント間の距離を、実際にデータポイントの拡張を計算せずに、直接計算する方法である。

サポートベクタマシンで広く用いられている高次元空間へのマップ方法が2つある。もとの特徴量の特定の次数までのすべての多項式（feature1 ** 2 * feature2 ** 5など）を計算する多項式カーネル（polynomial kernel）と、放射基底関数（radial basis function：RBF）カーネルとも呼ばれるガウシアンカーネルである。ガウシアンカーネルは、無限次元の特徴空間に対応するので説明が難しい。直観的には、ガウシアンカーネルではすべての次数のすべての多項式を考えるが、次数が高くなるにつれてその特徴量の重要性を小さくしているしかし、カーネル法を用いたSVMの背後にある数学の詳細は、実用上重要ではない。RBFカーネルを用いたSVMによる決定の様子を見るのは簡単だ。

2.3.7.3 SVMを理解する

訓練の過程で、SVMは個々のデータポイントが、2つのクラスの決定境界を表現するのにどの程度重要かを学習する。多くの場合、2つのクラスの境界に位置するごく一部の訓練データポイントだけが決定境界を決定する。これらのデータポイントをサポートベクタ（support vector）と呼ぶ。これがサポートベクタマシンの名前の由来である。
新しいデータポイントに対して予測を行う際に、サポートベクタとデータポイントとの距離が測定される。クラス分類は、このサポートベクタとの距離と、訓練過程で学習された個々のサポートベクタの重要性（SVCのdual_coef_属性に格納されている）によって決定される。データポイント間の距離は次のように定義されるガウシアンカーネルで測られる。

続きTIPSは書籍参照

2.3.7.4 SVMパラメータの調整

Cとgammmaの2つのパラメータを調整

SVMはうまく動く場合が多いのだが、パラメータの設定と、データのスケールに敏感であるという問題がある。特に、すべての特徴量の変異が同じスケールであることを要求する。

2.3.7.5 SVMのためのデータの前処理

カーネル法を用いたSVMでよく使われる方法は、すべての特徴量が0から1の間になるようにスケール変換する方法だ。

2.3.7.6 利点、欠点、パラメータ

カーネル法を用いたサポートベクタマシン（SVM）は、さまざまなデータセットに対してうまく機能する強力なモデルである。SVMを用いると、データにわずかな特徴量しかない場合にも複雑な決定境界を生成することができる。低次元のデータでも高次元のデータでも（つまり特徴量が少なくても多くても）、うまく機能するが、サンプルの個数が大きくなるとうまく機能しない。SVMは10,000サンプルぐらいまではうまく機能するが、100,000サンプルぐらいになると、実行時やメモリ使用量の面で難しくなってくる。

続きのTIPSは書籍参照

2.3.8 ニューラルネットワーク（ディープラーニング）

多層パーセプトロン（multilayer perceptrons: MLP）= フィードフォワード・ニューラルネットワーク

2.3.8 ニューラルネットワークモデル

2.4 クラス分類器の不確実性推定

クラス分類器が出力する予測クラスだけでなく、その予測がどのくらい確かなのかを知りたいことがよくある。
scikit-learnには、クラス分類器の不確実性推定に利用できる関数が2つある。decision_functionとpredict_probaである。

2.4.1 決定関数（Decision Function）

2クラス分類の場合、decision_functionの結果の配列は(n_samples,)の形になり、サンプルごとに1つの浮動小数点が返される。

この値には、あるデータポイントが「陽性」（この場合はクラス1）であると、モデルが信じている度合いがエンコードされている。正であれば陽性クラスを、負であれば「陰性」（つまり陽性以外）クラスを意味する。

2.4.2 確率の予測

predict_proba

predict_probaの出力は、それぞれのクラスに属する確率で、decision_functionの出力よりも理解しやすい。出力配列の形は、2クラス分類問題では、常に(n_samples, 2)になる。

2.4.3 他クラス分類の不確実性

decision_functionメソッドとpredict_probaメソッドは、多クラス分類に対しても利用できる

decisino_functinの結果は、（n_samples, n_classes）の形の配列になる。各列は個々のクラスに対する「確信度スコア」で大きいとそのクラスである可能性が高く、小さくなると可能性が低くなる
各データポイントに対して、確信度クラスが最大になるクラスを選ぶことで予測クラスが得られる

predict_probaの出力も、同じ(n_samples, n_classes)の形の配列となる。各クラスになる確率の和は1となる。

クラスの数だけ列がある場合には、列に対してargmaxを計算すれば、予測を再現できる。ただし、クラスが文字列だったり、0から始まる整数で表現されていない場合には、注意が必要だ。predictで得られた結果を、decision_functionやpredict_probaで得られた結果と比較する際には、クラス分類器のclasses_属性を使って、実際のクラス名を使うようにしなければならない。

from sklearn.datasets import load_iris

iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, random_state=42)

logreg = LogisticRegression()

# represent each target by its class name in the iris dataset
named_target = iris.target_names[y_train]
logreg.fit(X_train, named_target)

print("unique classes in training data:", logreg.classes_)
print("predictions:", logreg.predict(X_test)[:10])

argmax_dec_func = np.argmax(logreg.decision_function(X_test), axis=1)

print("argmax of decision function:", argmax_dec_func[:10])
print("argmax combined with classes_:",
      logreg.classes_[argmax_dec_func][:10])

unique classes in training data: ['setosa' 'versicolor' 'virginica'] 訓練データ中のクラス
predictions: ['versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor' 予測値
 'setosa' 'versicolor' 'virginica' 'versicolor' 'versicolor']

argmax of decision function: [1 0 2 1 1 0 1 2 1 1] 決定関数のargmax
argmax combined with classes_: ['versicolor' 'setosa' 'virginica' 'versicolor'
 'versicolor' 'setosa' 'versicolor' 'virginica' 'versicolor' 'versicolor'] 決定関数のargmaxをクラス名にしたもの

3章 教師なし学習と前処理

3.1 教師なし学習の種類

教師なし変換
クラスタリングアルゴリズム（clustering algorithms）

3.2 教師なし学習の難しさ

教師なし学習のアルゴリズムにはラベル情報がまったく含まれていないデータが与えられる。このため、出力がどうあるべきなのかわからない。
データサイエンティストがデータをよりよく理解するために、探索的に用いられる場合が多い。
教師あり学習の前ステップとしての利用が挙げられる

3.3 前処理とスケール変換

StandardScaler: 平均が0で分散が1になるように変換
RobustScaler: 中央値が0になり、四分位範囲（interquartile range、IQR）が1になるように移動・スケール変換する
MinMaxScaler: データがちょうど0から1の間に入るように変換
Normalizerは以下抜粋

個々のデータポイントを、特徴量ベクトルがユークリッド長1にになるように変換する。言い換えると、データポイントを、半径1の円（より高次元なら超球面）に投射する。したがって、すべてのデータポイントに対してそれぞれ異なるスケール変換が行われる（もとのユークリッド長の逆数をかける）。この変換は、特徴ベクトルの長さではなく、方向（もしくは角度）だけが問題になる場合に用いられる。

3.3.2 データ変換の適用

3.3.3 訓練データとテストデータを同じように変換する

fitは訓練データに対してして、テストデータにはしないように

3.3.4 教師あり学習における前処理の効果

3.4 次元削減、特徴量抽出、マニフォールド学習

3.4.1 主成分分析（PCA）

http://taustation.com/pca-lfw-dataset/

http://taustation.com/python-limiting-number-of-array-elements/

https://qiita.com/maskot1977/items/082557fcda78c4cdb41f

3.4.1.2 固有顔による特徴量抽出

3.4.2 非負値行列因子分解（NMF）

非負値行列因子分解（Non-negative matrix factorization：NMF）も、有用な特徴量を抽出することを目的とする教師なし学習手法である。このアルゴリズムの動作はPCAと似ており、やはり次元削減に用いることができる。

3.4.3 t-SNEを用いた多様体学習

https://blog.nownabe.com/2017/11/19/1185.html/

https://qiita.com/milk_soyyy/items/759c54eb4de12ac28288

3.5 クラスタリング

クラスタリングはデータセットを「クラスタ」と呼ばれるグループに分割するタスク

3.5.1 k-Means Clustrering

3.5.1.2　ベクトル量子化、もしくは成分分解としてのk-means

k-meansはクラスタセンタで個々のデータポイントを表現する。個々のデータポイントを、クラスタセンタとして与えられる単一の成分で表現していると考えることができる。このように、k-meansを単一成分で個々のデータポイントを表現する成分分解手法として見る考え方を、ベクトル量子化（vector quantization）と呼ぶ。

3.5.2　凝集型クラスタリング

凝集型クラスタリング（agglomerative clustering）とは、同じ原則に基づく一連のクラスタリングアルゴリズムである。これらのアルゴリズムは、個々のデータポイントをそれぞれ個別のクラスタとして開始し、最も類似した2つのクラスタを併合していく。これを何らかの終了条件が満たされるまで繰り返す。scikit-learnに実装されている終了条件はクラスタの数である。つまり、指定した数のクラスタだけが残るまで、似たクラスタを併合し続ける。「最も類似したクラスタ」を決定する連結（linkage）度にはさまざまものがある。この連結度は常に、2つの既存クラスタ間に定義される。
scikit-learnには次の3つが実装されている。

ward
average
complete

3.5.3　DBSCAN

3.5.4　クラスタリングアルゴリズムの比較と評価

3.5.4.1　正解データを用いたクラスタリングの評価

クラスタリングアルゴリズムの出力を、正解データクラスタリングと比較して評価するために用いられる指標がいくつかある。最も重要なものは、調整ランド指数（adjusted rand index：ARI）と正規化相互情報量（normalized mutual information：NMI）である。これらはいずれも定量的な指標で最良の場合に1を、関係ないクラスタリングの場合に0をとる（ただしARIは負の値になりうる）。

sklearn.metrics.cluster.adjusted_rand_score

3.5.4.2　正解データを用いないクラスタリングの評価

上でクラスタリングアルゴリズムを評価する1つの方法を示したが、実際にはARIのような指標を用いるには大きな問題がある。クラスタリングアルゴリズムを用いる際、実際には結果と比較するための正解データがない場合が多い。正しいデータのクラスタリングがわかっているなら、それを使って、クラス分類器のような教師ありモデルを作ればよい。したがって、ARIやNMIのような指標はアルゴリズムの開発過程でしか利用できず、アプリケーションがうまくいっているかどうかの指標にはならない。

正解データを必要としないクラスタリングの指標もある。シルエット係数（silhouette coefficient）などがそうだ。しかし、これらの指標は実際にはあまりうまくいかない。シルエットスコアは、クラスタのコンパクトさを計算する。大きい方がよく、完全な場合で1になる。クラスタがコンパクトなことは良いことだが、複雑な形状のクラスタはコンパクトにはならない。

もう少し良い評価方法として、頑健性を用いたクラスタリング評価指標がある。これらの指標では、ノイズをデータに加えたり、パラメータを変更したりしてアルゴリズムを実行し、結果を比較する。さまざまなパラメータや、ノイズのある入力に対しても同じ結果が帰ってくるなら、結果の信頼性が高いだろう、という発想だ。残念ながらこの手法は、本書を書いている時点ではscikit-learnには含まれていない。

3.5.4.3　顔画像データセットを用いたアルゴリズムの比較

Estimatorインターフェースのまとめ

4章 データの表現と特徴量エンジニアリング

連続特徴量 <-> カテゴリ特徴量 ≒ 離散値特徴量

continuous feature
categorical feature
discrete feature

特定のアプリケーションに対して、最良のデータ表現を模索することを、特徴量エンジニアリング（feature engineering）と呼ぶ。

4.1 カテゴリ変数

4.1.1 ワンホットエンコーディング（ダミー変数）

4.1.2 数値でエンコードされているカテゴリ

数値区分として表現されている値
1: 山
2: 川
3: 海
このような数値で表されているからといって連続値として扱ってはいけない。
意味的に順番がない場合には離散値として扱うべきだ

この対処方法は、DataFrameの列を数値から文字列に変換してしまう

demo_df['Integer Feature'] = demo_df['Integer Feature'].astype(str)
pd.get_dummies(demo_df, columns=['Integer Feature', 'Categorical Feature'])

4.2　ビニング、離散化、線形モデル、決定木

線形モデルを連続データに対してより強力にする方法の1つとして特徴量のビニング（binning）もしくは離散化（discretization）がある

ビニング例

bins = np.linspace(-3, 3, 11)
which_bin = np.digitize(X, bins=bins)

from sklearn.preprocessing import OneHotEncoder
# OneHotEncoderで変換する
encoder = OneHotEncoder(sparse=False)
# encoder.fitでwhich_binに現れる整数値のバリエーションを確認
encoder.fit(which_bin)
# transformでワンホットエンコードを行う
X_binned = encoder.transform(which_bin)

4.3　交互作用と多項式

特徴量表現をより豊かにするもう1つの方法として、特に線形モデルに有効なものが、もとのデータの交互作用特徴量（interaction feature）と多項式特徴量（polynomial feature）を加える方法である。

交互作用特徴量の例

特徴量とビン番号の積である。積の特徴量を、個々のビンにx軸の特徴量をそれぞれコピーしたと考えることもできる。

X_product = np.hstack([X_binned, X * X_binned])
reg = LinearRegression().fit(X_product, y)

多項式特徴量の例

ある特徴xに対して、x2、x3、x**4....を計算する

from sklearn.preprocessing import PolynomialFeatures

# x ** 10までの多項式を加える。
# デフォルトの"include_bias=True"だと、常に1となる特徴量を加える
poly = PolynomialFeatures(degree=10, include_bias=False)
print("Polynomial feature names:\n{}".format(poly.get_feature_names()))
> Polynomial feature names:
> ['x0', 'x0^2', 'x0^3', 'x0^4', 'x0^5', 'x0^6', 'x0^7', 'x0^8', 'x0^9', 'x0^10']”

poly.fit(X)
X_poly = poly.transform(X)
print("Entries of X:\n{}".format(X[:5]))
print("Entries of X_poly:\n{}".format(X_poly[:5]))

> Entries of X:
> [[-0.753]
 [ 2.704]
 [ 1.392]
 [ 0.592]
 [-2.064]]
> Entries of X_poly:
> [[    -0.753      0.567     -0.427      0.321     -0.242      0.182
      -0.137      0.103     -0.078      0.058]
 [     2.704      7.313     19.777     53.482    144.632    391.125...

4.4　単変量非線形変換

特徴量を2乗、3乗したものが、線形回帰モデルで有用であることを見た。他に特定の特徴量に有用であることがわかっている変換がある。log、exp、sinなどの数学関数を用いるものだ。決定木ベースのモデルは特徴量の順番しか見ないが、線形モデルやニューラルネットワークモデルは、個々の特徴量のスケールや分散と密接に結びついており、特徴量とターゲットに非線形関係があると、モデリングが難しくなる。これは特に回帰で顕著である。log、expなどの関数は、データの相対的なスケールを修正してくれるので、線形モデルやニューラルネットワークモデルでモデリングしやすくなる。「2章　教師あり学習」で、メモリ価格のデータでこの応用を見た。sin、cos関数は周期的なパターンを持つ関数を扱う際に有用だ。

このような変換が特に有効なよくあるケースは、整数のカウントデータを扱う場合だ。ここで言うカウントデータは、例えば「ユーザAは何回ログインしたか」というような特徴量のことだ。カウントデータは負であることはなく、多くの場合特定の統計的パターンに従う。

多くの場合は、特徴量の一部だけを変換することになる。特徴量ごとに別の変換を行わなければならない場合もある。前述の通り、この種の変換は決定木ベースのモデルには関係ないが、線形モデルにとっては本質的である。回帰モデルの場合は、ターゲット変数yも変換した方がよい場合もある。カウントデータ（例えば注文数など）の予測は一般的なタスクだが、log(y + 1)で変換するとうまくいくことも多い。

4.5 自動特徴量選択

データの次元数をもとの特徴量の数よりもはるかに大きくしたくなるかもしれない。しかし、特徴量を追加すると、モデルは複雑になり、過剰適合の可能性が高くなる。新しい特徴量を加える場合、また高次元データセット一般の場合、最も有用な特徴量だけを残して残りを捨てて、特徴量の数を減らすのは良い考えだ。こうすると、モデルが単純になり、汎化性能が向上する。しかし、どうしたら良い特徴量がわかるだろうか？ 基本的な戦略が3つある。単変量統計（univariate statistics）、モデルベース選択（model-based selection）、反復選択（iterative selection）の3つである。

4.5.1 単変量統計

p-値が大きすぎる = ターゲットと関係がなさそうだということを意味する

from sklearn.feature_selection import SelectPercenties

4.5.2 モデルベース特徴量選択

from sklearn.feature_selection import SelectFromModel

4.5.3 反復特徴量選択

from sklearn.feature_selection import RFE

4.6

LinearRegressionの...これは曜日や時刻が整数でエンコードされていて、連続値として解釈されているからだ。線形モデルは時刻に対する線形関数としてしか学習ができないので、時刻が遅いほどレンタル数が大きくなると学習してしまっている。しかし、実際のパターンははるかに複雑だ。整数をOneHotEncoderを用いて変換することで、カテゴリ変数として解釈すれば、パターンを捉えることができる

5章 モデルの評価と改良

5.1 交差検証

cross-validation

k分割交差検証（k-fold corss-validation）

データの分割を何度も繰り返して行い、複数のモデルを訓練する。

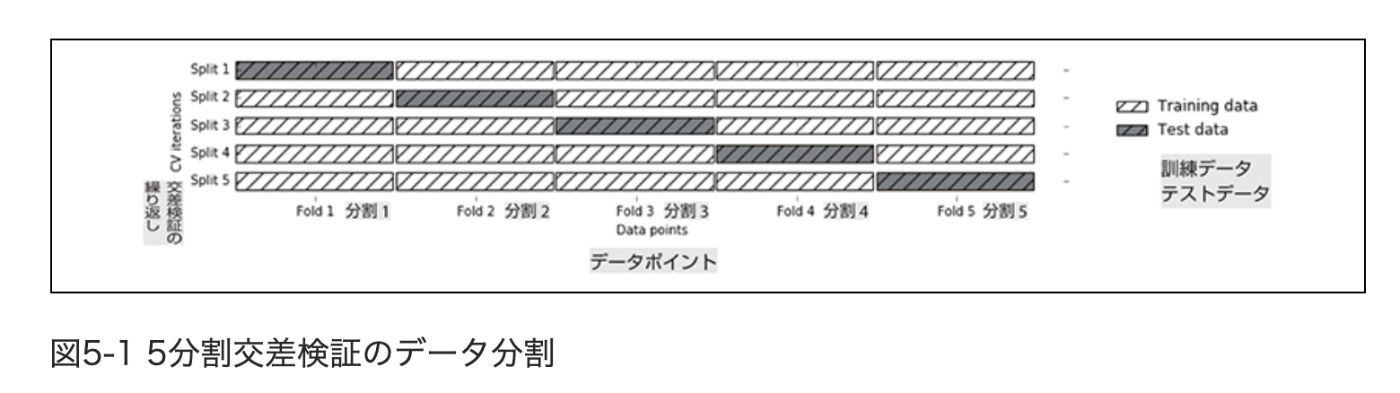
5.1.1 scikit-learnでの交差検証

from sklearn.model_selection import cross_val_score

5.1.2 交差検証の利点

交差検証は新しいデータに適用するためのモデルを作る方法ではないということに注意しておこう。交差検証はモデルを返さない。cross_val_scoreを呼び出すと内部的には複数のモデルが構築されるが、交差検証の目的は、与えられたアルゴリズムが特定のデータセットに対してどの程度汎化できるかを評価することだけにある。

5.1.3 層化k分割交差検証

5.1.3.1 交差検証のより詳細な制御

scikit-learnでは、cvパラメータに交差検証分割器（cross-validation splitter）を与えるとことでデータの分割方法より詳細に制御することができる

ほとんどの場合は、回帰にはk分割交差検証、クラス分類には層化k分割交差検証というデフォルトの動作でうまくいく。しかし、別の戦略を取りたくなることもあるだろう

5.1.3.2 1つ抜き交差検証

leave-one-out

from sklearn.model_selection import leaveOneOut

5.1.3.3 シャッフル分割交差検証

shuffle-split cross-validation

from sklearn.model_selection import ShuffleSplit

層化バージョンもあり、StratifieldShuffleSplit

5.1.3.4 グループ付き交差検証

密接に関係するグループがある場合に用いられる交差検証の設定がある。
訓練セットとテストセットに含まれている人が重ならないように

from sklearn.model_selection import GroupKFold
# create synthetic dataset
X, y = make_blobs(n_samples=12, random_state=0)
# assume the first three samples belong to the same group,
# then the next four, etc.
groups = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
scores = cross_val_score(logreg, X, y, groups=groups, cv=GroupKFold(n_splits=3))
print("Cross-validation scores:\n{}".format(scores))
> Cross-validation scores:
> [0.75  0.6   0.667]

上のプログラムのイメージ図

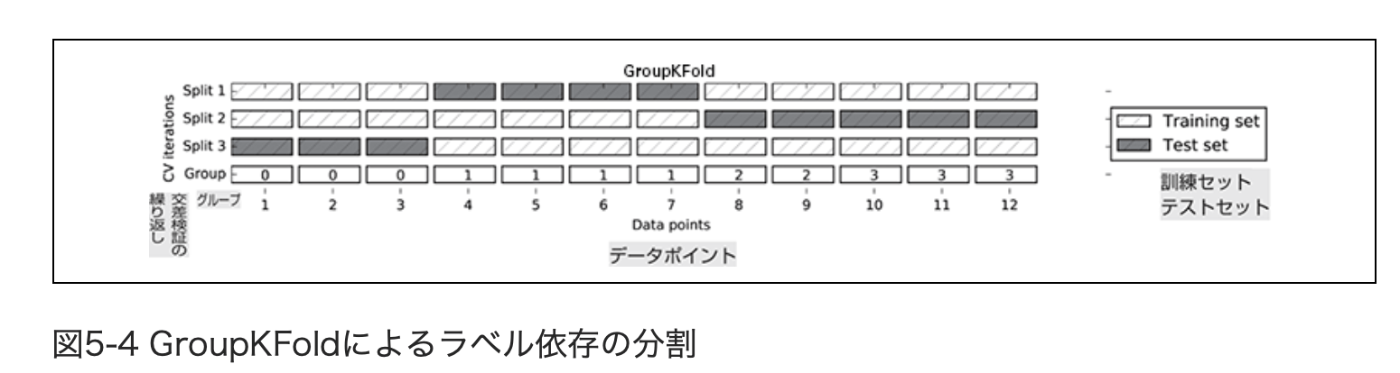
5.2 グリッドサーチ

5.2.2 パラメータの過剰適合の危険性と検証セット

訓練セット、検証セット、テストセットを区別することは機械学習を実運用する上で根本的に重要なことである。テストセットの精度にもとづいて何らかの選択をすることは、テストセットからモデルへ情報が「漏洩」することになる。したがって、テストセットを分離しておき、最後の評価にだけ用いるようにしなければならないのだ。すべての探索的な解析とモデル選択を訓練セットと検証セットだけで行い、テストセットは最後の評価にとっておくとよいだろう。探査的可視化だけの場合でもこれは重要だ。厳密に言えば、テストセットで2つ以上のモデルで評価して良いほうを選ぶだけでも、モデルの精度を楽観的に見積もりすぎることになる。

5.2.3 交差検証を用いたグリッドサーチ

from sklearn.model_selection import GridSearchCV

5.2.3.1 交差検証の結果の解析

scores = np.array(results.mean_test_score).reshape(6, 6)

# plot the mean cross-validation scores
mglearn.tools.heatmap(scores, xlabel='gamma', xticklabels=param_grid['gamma'],
                      ylabel='C', yticklabels=param_grid['C'], cmap="viridis")

5.2.3.1 グリッドでないサーチ空間

GridSearchCVは、通常すべてのパラメータのすべての組合せに対して試行を行うが、これが適さない場合もある。例えば、SVCにはkernelというパラメータがあり、このパラメータで選択されるカーネルに応じて他のパラメータが定まる。例えばkernel='linear'であれば、モデルは線形になり、パラメータCのみが使われる。kernel='rbf'の場合には、パラメータCとgammaが使われる（他のパラメータ、例えばdegreeは使われない）。このような場合、Cとgammaとkernelのすべての組合せに対してサーチしても意味がない。kernel='linear'の場合、gammaは使われないので、gammaを変化させて試行することは時間の無駄だからだ。このような「条件付き」パラメータを扱うために、GridSearchCVは、param_gridとしてディクショナリのリストを受け付けるように作られている。リスト中の個々のディクショナリが独立したグリッドに展開される。カーネルとパラメータの組合せに対するグリッドサーチは以下のように書ける。

param_grid = [{'kernel': ['rbf'],
               'C': [0.001, 0.01, 0.1, 1, 10, 100],
               'gamma': [0.001, 0.01, 0.1, 1, 10, 100]},
              {'kernel': ['linear'],
               'C': [0.001, 0.01, 0.1, 1, 10, 100]}]

grid_search = GridSearchCV(SVC(), param_grid, cv=5,
                          return_train_score=True)

X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, random_state=0)

grid_search.fit(X_train, y_train)
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.2f}".format(grid_search.best_score_))

5.2.3.3 異なる交差検証手法を用いたグリッドサーチ

GridSearchCVは、cross_val_scoreと同様に、デフォルトではクラス分類には層化k分割交差検証を、回帰にはk分割交差検証を用いる。
cross_val_scoreに関して述べたのと同様に、交差検証の分割器をcvパラメータとしてわたすことができる。特に、訓練セットと検証セットへの分割を一度だけにするには、ShuffleSplitもしくはStratifiedShuffleSplitを用いてn_iter=1とするとよい。この方法は、データセットが非常に大きい場合や、モデルの計算に非常に時間がかかる場合に有用である。

5.2.3.4 ネストした交差検証

しかし、上で見たGridSearchCVを用いる例では、データを訓練セットとテストセットに一度だけ分けている。これでは、データの一度だけの分割に結果が依存してしまい、不安定になる可能性がある。ここで、手法を一歩進めて、もとのデータを訓練セットとテストセットに一度だけ分けるのではなく、交差検証で何度も分割することを考える。この手法をネストした交差検証と呼ぶ。

ネストしていないテスト検証

param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
              'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), param_grid, cv=5,
                          return_train_score=True)

X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, random_state=0)

grid_search.fit(X_train, y_train)

ネストした交差検証

param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
              'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5),
                         iris.data, iris.target, cv=5)
print("Cross-validation scores: ", scores)
print("Mean cross-validation score: ", scores.mean())
> Cross-validation scores:  [0.967 1.    0.967 0.967 1.   ]
> Mean cross-validation score:  0.9800000000000001

5.2.3.5　交差検証とグリッドサーチの並列化

GridSearchCVとcross_val_scoreでは、パラメータn_jobsに利用したいコア数を設定することで、複数のコアを利用することができる。n_jobs=-1を設定すると利用できるすべてのコアを利用する。
scikit-learnではネストした並列実行はサポートされていないことに注意しよう。したがって、モデル（例えばランダムフォレスト）でn_jobsオプションを使っていたら、GridSearchCVでは使うことができない。

5.3 評価基準とスコア

5.3.2.3 混同行列

再現率（recall） = 感度（sensitivity） = ヒット率（hit rate） = 真陽性率（true positive rate: TPR）とも呼ばれる

from sklearn.metrics import classificatoin_report

@TODO あとでまた見てみる