1-2. 基数変換

抜粋: m進数から10進数に変換する

def any2dec(target, m):
    n = len(target)-1 # 指数の最大値
    sum = 0           # 10進数に変換した値
    
    # 文字数分の繰り返し
    for i in range(len(target)):
        if target[i] == 'A':     num = 10
        elif target[i] == 'B':   num = 11
        elif target[i] == 'C':   num = 12
        elif target[i] == 'D':   num = 13
        elif target[i] == 'E':   num = 14
        elif target[i] == 'F':   num = 15
        else:                    num = int(target[i])
            
        sum += (m ** n) * num  # 「mのn乗×各桁の値」を合計
        n -= 1  # 重みを1つ減らす
    return sum

他参考

https://iatlex.com/python/base_change

ta.toshio

1-4. 負の数の表し方

コンピューターの世界で、負の数は「2の補数」で表現されます。

参考
https://medium-company.com/2の補数/

4桁の符号ビット付き2進数	10進数
0111	7
0110	6
0101	5
0100	4
0011	3
0010	2
0001	1
0000	0
1111	-1
1110	-2
1101	-3
1100	-4
1011	-5
1010	-6
1001	-7
1000	-8

ta.toshio

2-3. コンピュータに特有のビット演算

ビット演算

>>> bin(0b10101010 & 0b00001111)
'0b1010'

pythonでは、ビット演算は10進数の値でも実行できる、とのこと

>>> 170 & 15 # 2進数の「10101010」と「00001111」をAND演算
10 # 2進数の「1010」

2の補数を求める

>>> ~10 + 1 #10進数のすべてのビットを反転（NOT演算）して、1を足す
-10

>>> bin(-10)
'-0b1010' # コンピュータの内部で使っている2の補数とは違う値。あくまで10の2進数に「-」がついている表現

>>> bin(-10 & 0b11111111) # 10（10進数）と11111111（2進数）をAND演算し、結果を2進数で表示
'0b11110110' # -10を表す2の補数

>>> bin(-10 & 0xFF)# 「11111111」は16進数の「FF」
'0b11110110'

一番下に表示されている「11110110」-10を表す2の補数にすべて1のビット演算のマスクをかけると'-0b1010'に表示されずに'0b11110110'に表示される。ちょっとしたTIPSみたいなものだと思う

以下のマスクをかけて一部を取り出すビット演算の例がおもしろい

def get_pixel_color(c):
    r = (c & 0x00FF0000) >> 16 # 赤
    g = (c & 0x0000FF00) >> 8  # 緑
    b = (c & 0x000000FF)       # 青
    return r, g, b

c = 4287090426  # 色情報（10進数）
r, g, b = get_pixel_color(c) # get_pixel_color()関数を実行
print(r, g, b)

ta.toshio

3-3 直線の方程式

3-2 直交する2本の直線

y = a1x + b1とy = a2x + b2 という直線の式が2つあるとき、

a1 = a2 であれば2つの直線は平行になる。直線の平衡条件
a1 * a2 = -1のとき2つの直線は垂直に交わる。直線の直行条件

2直線の交点を求める

from sympy import Symbol, solve

x = Symbol('x')  # 文字の定義
y = Symbol('y')

ex1 = -3/2*x + 6 - y  # 直線1の式
ex2 = 1/2*x + 2 - y   # 直線2の式

print(solve((ex1, ex2)))  # 連立方程式を解く
{x: 2.00000000000000, y: 3.00000000000000}

3-4 比例式と三角比

4-1 比例式の性質

1:200 = 2.5:x <- 比例式

比例式には内項と外項を掛けた値が等しいという性質がある

書籍から拝借

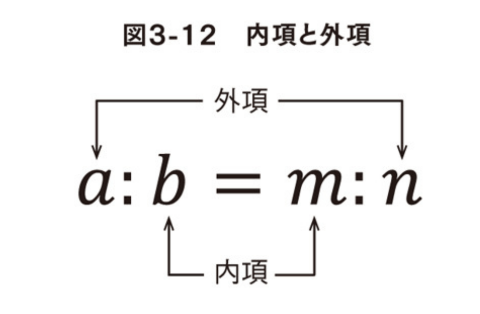
4-2 線分をm:nに内分する点

参考
https://math-travel.com/highanaibun/

線分を垂直に二等分する直線

アルゴリズム

線分の傾きを求める
線分の中点を求める
線分と直交する直線の傾きを求める
2でも求めた座標と3で求めた傾きを直線の式に代入して、切片を求める

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# 基となる線分の傾きと切片
a1 = (5-1)/(6-0) # yの増加量 / xの増加量
b1 = 1

# 線分の中点
cx = (0 + 6) / 2
cy = (1 + 5) / 2

# 線分に直交する直線の傾き(a2 = -1/a1)
# a1a2 = -1 -> a2 = -1 / a1
a2 = -1 / a1

# 線分に直交する直線の切片(b2 = y - a2*x)
b2 = cy - a2*cx

# 直線の式
x = np.arange(0, 7)   # xの値
y1 = a1*x + b1   # もとの直線
y2 = a2*x + b2   # 垂直二等分線

# 描画
plt.plot(x, y1)
plt.plot(x, y2)
plt.axis('equal') 
plt.grid(color='0.8')
plt.show()

4-3 三角比と円

直角三角形は、直角以外の角が1つ決まれば三角形の形が決まる。

相似比
三角比
三角関数

解説は書籍参照。

sin, cos, tan参考

三角比を使って円を描画

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# 角度
th = np.arange(0, 360)

# 円周上の点Pの座標 
x = np.cos(np.radians(th))
y = np.sin(np.radians(th))

# 描画
plt.plot(x, y)
plt.axis('equal')
plt.grid(color='0.8')
plt.show()

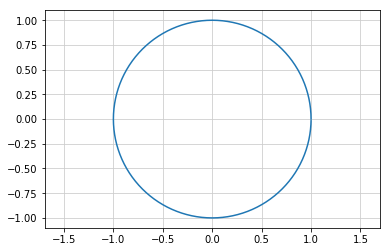
弧度法

円に対する弧の長さの比率で角度を表す方法

360 : 2π = 60 : x
360x = 2π * 60
x = 1/3π

直角をはさむ2辺の比から角度を求める

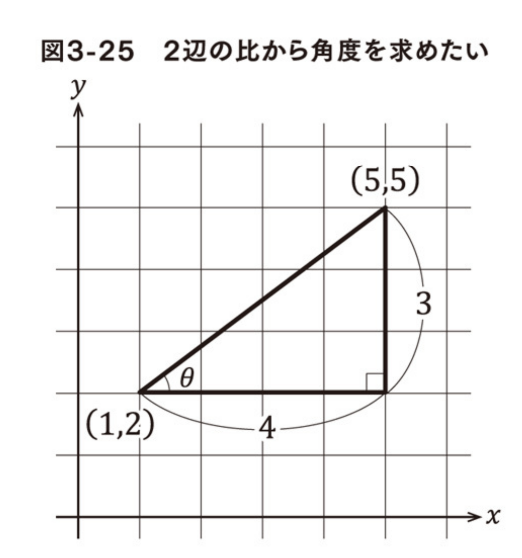
rad = np.arctan2(3, 4)  # 角度を求める（ラジアン）
print(rad)
th = np.degrees(rad)    # 度数法に変換
print(th)
0.6435011087932844
36.86989764584402

アークタンジェントとは

https://univ-study.net/arctan/

3-5 三平方の定理

5-1 円の方程式

斜辺の長さ2乗 = 残り2辺の長さの2乗して足したもの


%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# 円の方程式
r = 300  # 半径
x = np.arange(-r, r+1)    # x: -300～300
y = np.sqrt(r**2 - x**2)  # y

# 描画
plt.plot(x, y)
plt.axis('equal') 
plt.grid(color='0.8')
plt.show()

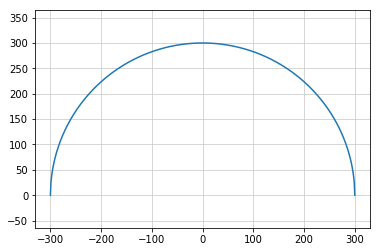
円の中心が座標の原点以外の時 -> 書籍参照

5-2 2点間の距離

書籍参照

画像から実際の長さを求める方法

書籍参照

写真から実寸法を求めたいときの考え方がおもしろい
物差しの10cmが30ピクセルだとしたら 10:30 = x: 224（224は書籍内で求めたピクセル距離）
x = 224 * 10 / 30

3-6 便利な公式

6-1 点から直線までの距離

https://manabitimes.jp/math/857

別解アルゴリズム

与えられた直線と直行する直線の式を求める
基となる直線と1で求めた直線の好転を求める
与えられた点と2で求めた交点間の距離を求める

6-2 直線で囲まれた領域の面積

ヘロンの公式

https://atarimae.biz/archives/25057

円を描く方法いろいろアルゴリズム

円の中心と円周上の1点を指定する方法

与えられた2点間の距離（半径）を求める
1点目を円の中心、1でも求めた値を半径とする円を描画する

正方形の対角を2点指定する方法

与えられた2点の中点（円の中心）を求める
1で求めた点と、2点目を通って、y軸と平行な直線との距離（半径）を求める
1で求めた点を円の中心、2で求めた値を半径とする円を描画する

円周上の3点を指定する方法

与えられた3点から、各辺の式を求める
各辺の垂直二等分線の式を求める
垂直二等分線の交点を求める
3で求めた点と、与えられた1つの点との距離（半径）を求める
3で求めた点を円の中心、4で求めた値を半径とする円を描画する

ta.toshio

4 ベクトル

1-2 ベクトルの成分

座標の原点を始点とするベクトルを位置ベクトルと言う

1.3 ベクトルの方向

ベクトルのx成分とy成分がわかっていて、x軸とベクトルがなす角度θはtanの逆関数を使って求められる

https://rikeinvest.com/math/gyakukansu/

https://univ-study.net/arctan/

1.4 ベクトルの大きさ

三平方の定理で求められる

ベクトルの大きさはスカラーと言う

大きさ1のベクトルを単位ベクトルと言う

1.5 ベクトルの演算

2 ベクトルの方程式

2.1 直線の表し方

ベクトルP = ベクトルa + kベクトルv

2.2 2直線の交点

2.3 ベクトルを使う理由

二次元であっても、三次元であっても、
空間上のベクトル方程式は p = a + kv のままです。
同じ計算方法で解けるというのがベクトルを使う最大の理由です。

3 ベクトルの内積

3.1 貢献度を計算する

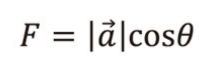
3.2 仕事の量を計算する

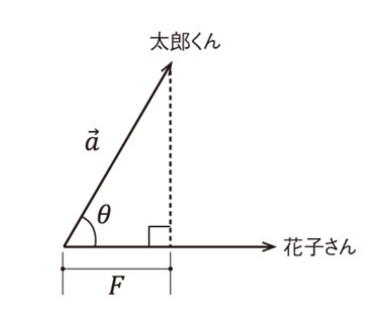
物理の世界では...、計算方法は「力の大きさ x 移動距離」

ベクトルの内積

「力の大きさ x 移動距離」で計算する方法、数学の世界ではベクトルの内積と言い、ドット（・）を使って、

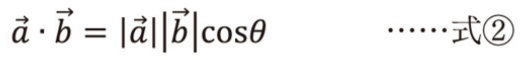
ベクトルacosθは、ベクトルaの方向に引っ張った時に水平方法に働く力(F)、ベクトルbはその方向に動いた距離です。

ベクトルの成分がわかっているとき、

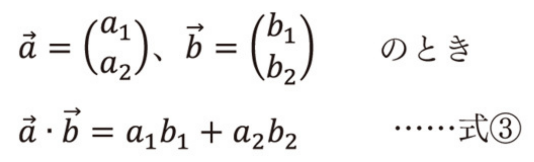
3.4 2直線のなす角

内積を利用すると2つのベクトル間の角度が求められる

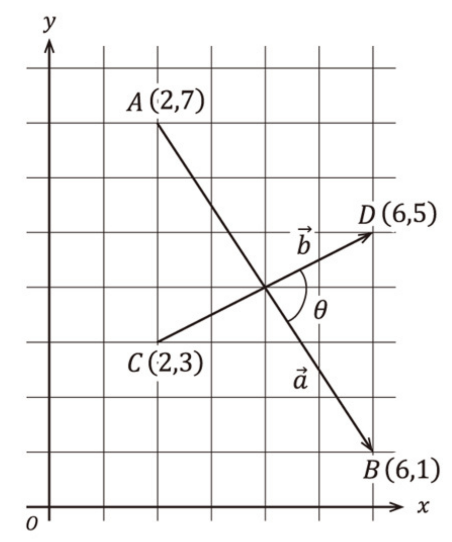
import math
import numpy as np

# 座標
a = np.array([2, 7]) 
b = np.array([6, 1])
c = np.array([2, 3])
d = np.array([6, 5])

# ベクトルaとベクトルbの成分
va = b - a
vb = d - c

# ベクトルの大きさ
norm_a = np.linalg.norm(va)
norm_b = np.linalg.norm(vb)

# ベクトルの内積
dot_ab = np.dot(va, vb)

# 角度を求める
cos_th = dot_ab / (norm_a * norm_b)
rad = math.acos(cos_th)
deg = math.degrees(rad)
print(deg)

3.5 内積の性質

内積の結果を見ると2つのベクトルの位置関係がわかる

参考・解説

私たちが頭の中でイメージできるのは三次元空間まででです
四次元以上のベクトルは、順番を持つ数の集まりと考えるようにしましょう

4 ベクトルの外積

外積は2つのベクトルに垂直なベクトルになる
そのベクトルの大きさは、2つのベクトルが作る平行四辺形の面積と等しい

この章で伝えていること

4.1 法線ベクトル

import numpy as np
a = np.array([0, 1, 2])  # ベクトルaの成分
b = np.array([2, 0, 0])  # ベクトルbの成分
np.cross(a, b)           # 外積

4.2 面積を求める

外積の結果できるベクトルの大きさは、2つのベクトルがつくる平行四辺形の面積と等しい

a = np.array([2, 4])  # ベクトルaの成分
b = np.array([3, 1])  # ベクトルbの成分
cross_ab = np.cross(a, b)     # 外積を求める
s = np.linalg.norm(cross_ab)  # ベクトルの大きさを求める（平行四辺形の面積）
s / 2   # 三角形の面積

この章で学んだベクトルのこと全般

ta.toshio

5 行列

2 行列の演算

足し算と引き算ができるのは行列の形が等しい行列同士

2.2 行列の実数倍

行列の実数倍では次の計算法則が成り立つ

交換法則
結合法則
分配法則

2.4 掛け算のルール

掛け算ん計算法則

結合法則
分配法則

交換法則は成立しない

2.7 逆行列と連立方程式

連立方程式を行列で表す

未知数の係数で作った行列の逆行列を求める

求めた逆行列を1の両辺に掛ける

逆行列で連立方程式を解く

A = np.matrix([[5, 3], [2, 1]])  # 行列A（未知数の係数で作った行列）
inv_A = np.linalg.inv(A)   # 行列Aの逆行列
B = np.matrix([[9], [4]])  # 行列B（連立方程式の右辺）
inv_A * B  # 逆行列×行列B

逆行列を関数使わずに公式を使って

a = 5  # 行列A（未知数の係数）
b = 3
c = 2
d = 1
s = 9  # 行列B（連立方程式の右辺）
t = 4
k = a*d - b*c  # 逆行列の各要素の分母
x = ((d/k)*s) + ((-b/k)*t)  # 逆行列×行列B
y = ((-c/k)*s) + ((a/k*t))
x, y

3 図形の一次変換

ベクトルに行列を掛けると新たなベクトルになる -> ベクトルを座標で表すと、座標Aに行列を掛けると座標A'になる。

(1)写像のうちで同一集合から同一集合への対応となっているものを変換といいます．
(2)平面上の点(x, y)を点(x', y' )に移す変換fが次の式で表されるとき，この変換fを1次変換（線形変換）という．

(抜粋: https://www.geisya.or.jp/~mwm48961/linear_algebra/linear_transform1.htm)

座標を変換するための行列は変換行列と言います。

3.2 図形の対称移動

3.3 図形の拡大と縮小

3.4 図形の回転

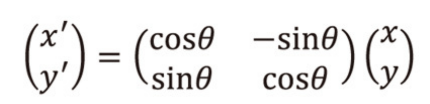
この式の解説は書籍参照

3.5 図形の並行移動

3.6 2x2行列から3x3行列へ

回転、拡大・縮小は乗算で計算するが、平行移動は加法する必要がある。加法が入る入ることによって複雑になる。

この問題を解決するために、CGの世界では同次座標という方式が用いられている。

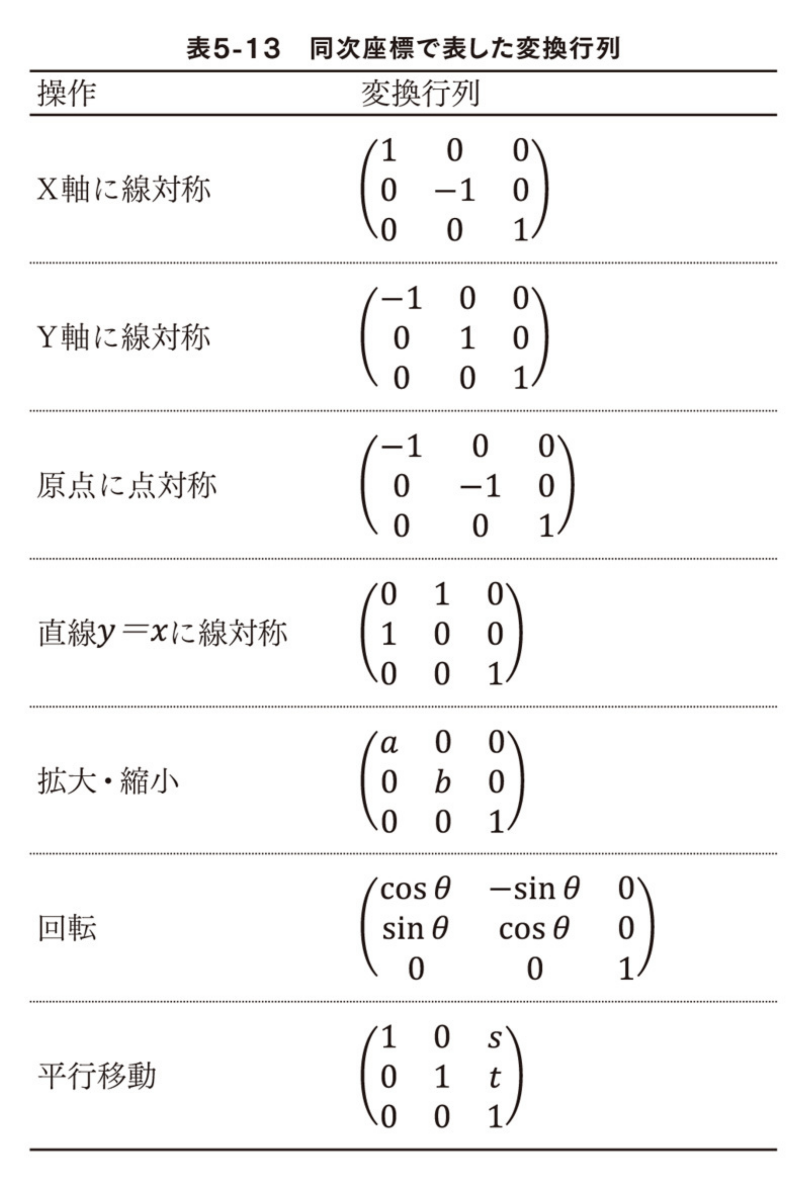
3.7 一次変換の組み合わせ

ta.toshio

6 集合と集合

1 集合

集合、はっきりと区別できて、同じ性質を持ったデータの集まり

1.2 いろいろな集合

ある明確な条件に基づいてグループ分けをすることを集合演算と言います。

部分集合
補集合
全体集合

積集合: 2つの集合に共通する要素の集合を積集合と言い、A ∩ B のように表す。
和集合: A ∪ B
差集合: 一方の集合から、もう一方の集合を引いたもの

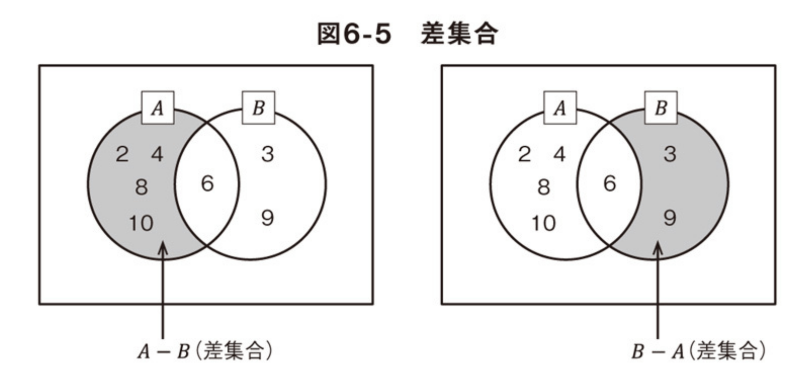
対象差

2 順序と組み合わせ

2.1 場合の数

起こり得る事象の数を場合の数

2.2 場合の数の求め方

積の法則
和の法則

2.3 順列

樹形図
順列（permutation）

2.4 階乗

1からnまでの自然数をかけあわせたものを、...階乗と言います

円順列、場合の数は(n - 1)!

左回りと右回りを区別しない方法を「じゅず順列」と言い、場合の(n - 1)! / 2で求めることができます

2.5 重複順列

重複順列

itertoolsモジュールのproduct()関数を使って調べることができます

2.6 組み合わせ

Cはcombination
n個から順番を考慮せずにr個を取り出すときの場合の数

組み合わせが何通りかを調べるときは、itertoolsモジュールのcombinations()関数を使います。

3 確率

3.1 確率の求め方

p: probability

3.2 数学的確率と統計的確率

3.3 積の法則と和の法則

3.4 モンテカルロ法

「モンテカルロ法」は確率を使って、確率とはまったく関係のない問題を解く手法です。

ここでは円周率を求める例をあげていた

ta.toshio

7 統計と乱数

1 統計とは

1.1 母集団と標本

1.2 データのばらつき具合を見る

度数分布図 = ヒストグラム
分布 = ばらつき状態

1.3 平均値、中央値、最頻値

中央値 = 中間値 = 中位数 = median()
最頻値 = モード

# 平均値、中央値
print('平均値', np.mean(dat['数学']))
print('中央値', np.median(dat['数学']))

# 最頻値
bincnt = np.bincount(dat['数学'])  # 同じ値の個数を数える
mode = np.argmax(bincnt)  # bincntの中で最も大きな値を取得
print('最頻値', mode)

1.4 度数分布図

階級 = データの取りうる範囲を等間隔で分ける
度数 = 各階級に含まれるデータ数を数える

2 ばらつきを調べる

2.1 分散と標準偏差

分散 == (データ - 平均)² の合計 / データ数
標準偏差 = 分散の平方根

平均: np.mean(x)
分散: np.var(x) # Variance
標準偏差: np.std(x) # Standardization

2.2 偏差値

標準化は平均値が0、分散が1になるようにデータを変換する作業で、そのための式が
標準化後のデータ = データ - 平均 / 標準偏差

1σ（σ）は標準偏差1つ分

偏差値 = データ / 平均 / 標準偏差 * 10 + 50

3 関係を調べる

3.1 散布図

散布図とは、2つのデータの関係性を表す図です。
右上がり...正の相関
右下がり...負の相関

plt.scatter(x, y)

3.2 共分散と相関係数

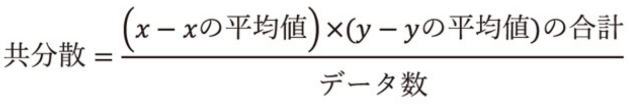
相関係数はnp.corrcoef(x, y)で求められる。

4データから推測する

4.1 移動平均

# 区間数:9 の移動平均
v = np.ones(9)/9.0
y2 = np.convolve(y, v, mode='same')  # 移動平均を求める
plt.plot(x[4:n-4], y2[4:n-4])        # グラフを描画
plt.show()

4.2 回帰直線

「ずれ」を2乗してから合計...この値が最も小さくなるような直線を回帰直線

mean_x = np.mean(x) # xの平均
mean_y = np.mean(y)
cov = np.mean(x - mean_x) * (y - mean_y) # xとyの共分散
var_x = np.var(x) # xの分散
a = cov / var_x # 傾き
b = mean_y - (a * mean_x)

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# データ
x = np.array([23,24,28,24,27,21,18,25,28,20])  # 気温
y = np.array([37,22,62,32,74,16,10,69,83,7])   # ジュースの販売数

# 回帰直線
a, b = np.polyfit(x, y, 1)
y2 = a * x + b
print('傾き: {0}, 切片:{1}'.format(a, b))

# 描画
plt.scatter(x, y)  # 散布図
plt.plot(x, y2)    # 回帰直線
plt.show()

5 ランダムに値を選ぶ

5.1 乱数

乱数を過信してはいけません。なぜなら、コンピュータが生成した乱数は何らかの計算式で求めた値だからです。これを「疑似乱数」と言います。

5.2 乱数を使うときに注意すること

乱数を生成する式の1つに、「線形合同法」

乱数の種（シード: seed）

randomモジュールのrandint関数も、システム時刻を使って乱数の種を初期化しています。

ta.toshio

第8章微分・積分

1 曲線とグラフ

2 微分とは

「微分する」...これは「変化の様子を見る」という意味です。

微分係数 = 関数f(x)の導関数 = y = f(x)のx = aにおける接線の傾き

2.5 導関数が教えてくれること

極値
極小、極大、変曲点

積分

積分は面積を扱う
積分は微分の逆演算

3.1 変化を積み重ねる

3.2 積分する

連続して変化する値を足して、合計を求める

3.3 定積分・不定積分

範囲を決めて積分することを、...定積分と言い、
$\int_{a}^{b} f(x)dx$
のように表記
「f(x)にaからbまでの範囲で、ごく小さなdxを入れて積分する」という意味

範囲を指定しない次の式は不定積分
$\int f(x)dx$

3.4 原始関数

微分してf(x)になる関数のことを原始関数

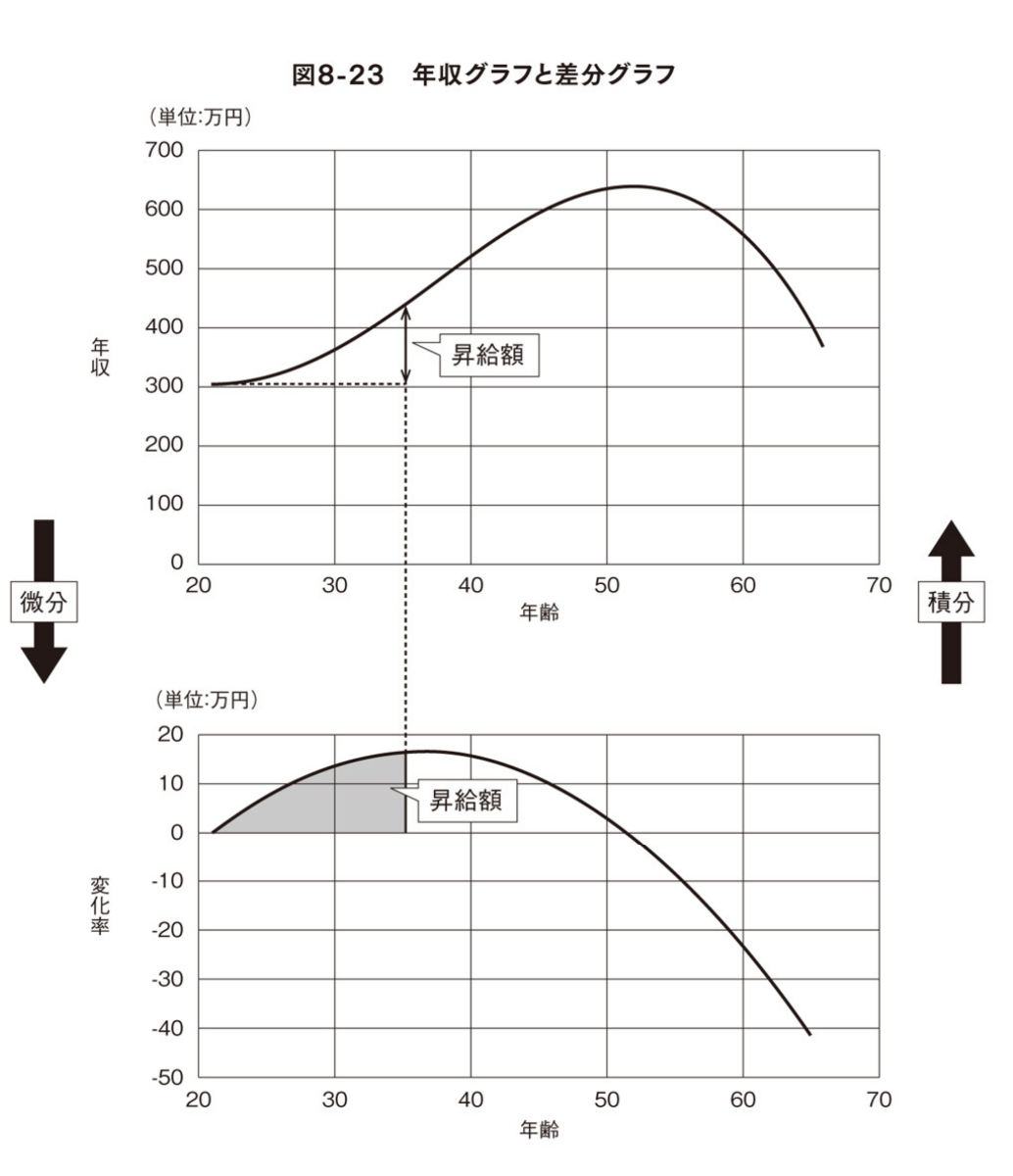
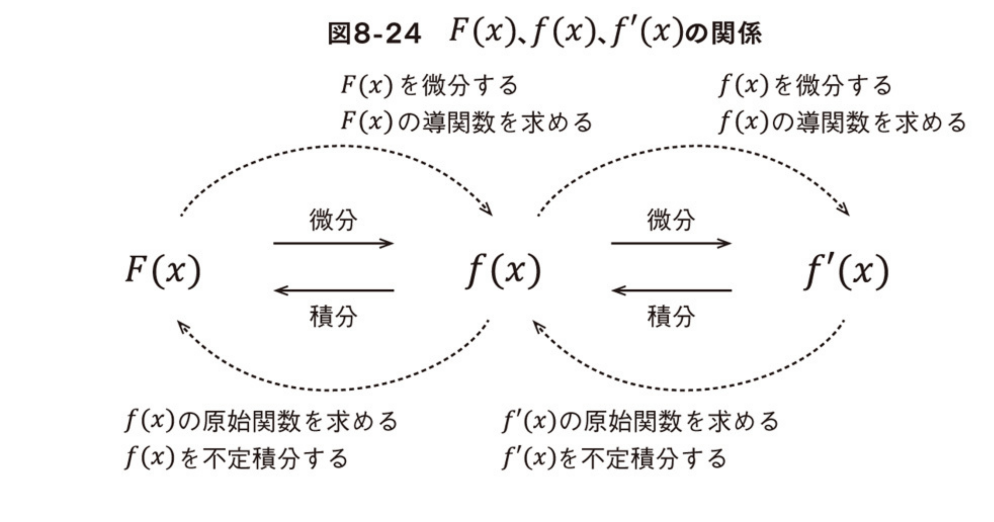
3.5 積分の公式

3.6 積分定数Cとは

4 道具としての微分・積分

微分は変化の様子を知るための道具
積分はごく小さな部分の合計を知るための道具

4.1 曲線の接線

ベジェ曲線のなめらかさを表現するために終点と始点の接線が等しいことを紹介

4.2 輪郭の抽出

隣り合うピクセルの色情報とを比べて輪郭を描画しているプログラムを紹介

4.3 円周と円の面積の関係

2πrを積分するとπr²
πr²を微分すると2πr

トイレットペーパーの長さを計算するプログラムを紹介

4.4 円錐の体積

円錐の体積 1/3πr²hの紹介