[後編] 機械学習超入門視聴メモ
順不同メモ
セクション6 PCA(主成分分析)
主成分分析は次元削減の手法。
次元というのは、特徴量の数だと思って
特徴量が多すぎるとバリアンスが高くなって過学習気味になる
また、次元が多いと(高次元という表現)、学習やデータの処理に時間がかかったり、データの可視化することができなってしまうので、次元を削減する
-> 処理の高速化とデータの可視化のために用いられる
- PCAは、高次元から低次元へと変換するアルゴリズム
- すべての特徴量を使用して低次元に変換する(Lassoのように重要でなさそうな特徴量を落とすアルゴリズムではない)
- Lassoのような特徴量選択の手法としては使用されない
主成分(pricipal component)
- データが最も情報を持っている、つまりは最も分散している方向を探す(この方向のことを主成分と呼ぶとのこと)
- 最初の主成分を第1主成分
- アルゴリズムは第1主成分と直交する方向の中から、最も情報を持っている方向を探す(別の主成分) = データを射影した時に最も情報を持っている
- これらの主成分はデータの特徴をよりよく掴んだ新たな座標軸といえる
- 第n主成分は第n-1主成分と直交する軸の中で最も分散している軸
- 各主成分のデータを射影し、次元を圧縮する
参考


疑問
Variance(分散)が最小になる値を求めたいのに
-> ラグランジュの未定乗数法を使う
法線ベクトルの関係から以下の式が成り立つ、の意味がよく分からなかった。公式?
f(x, y)の等高線の法線ベクトルはg(x, y) = 0の法線ベクトルと同方向になる
->f(x, y) = -λ \nabla g(x, y) \nabla
以下のこと?
法線ベクトルと直線の方程式
ベクトル 𝑛⃗ =(𝑎,𝑏) に垂直で、点(𝑥1,𝑦1) を通る直線の方程式は
𝑦−𝑦1=−(𝑥−𝑥1) \dfrac{a}{b}
ラグランジュの未定乗数法を使った結果
λu = Su が導き出せる。(@TODO ここの式展開あとで書く)
これはλは行列Sの固有値(eigenvalue)、uを固有ベクトル(eigenvector)ということを表す
つまりPCAは分散共分散行列Sの固有ベクトルuを求めればよい
PCAの手順
特徴量Xを
- 標準化する(特徴量によってスケールが異なると、公平にそれぞれの分散を比較できない)
- 分散共分散行列を求める
- 固有ベクトルと固有値を求める(大きい順に第一主成分、第二主成分...と並べる)
- 主成分の座標系に変換 -> 固有ベクトルとxの内積
寄与率と累積寄与率
pca.components_
第一主成分、第二主成分...の特徴量空間におけるそれぞれの主成分のベクトル(分散共分散行列の固有ベクトルを表す)
他参考
6 - 49 共分散と分散共分散行列
2変数間の相関関係
共分散
共分散を標準化した値が相関係数
分散共分散: 複数の変数間の分散と共分散を行列にしたもの
セクション7: クラスタリング
60 教師あり学習 / 教師なし学習
類似しているデータをグループ(クラスタ)にしてデータを分類する
クラスタリングは教師なし学習
学習するアルゴリズム
- k-means
- 階層クラスタリング
61 k-means
- データをk個のクラスタに分類する
- クラスタ内の分散の合計が全体で最小になるようにする
k-meansの損失関数
- 全クラスタ内の各データ同心の差の平方和(クラスタ内分散)の合計を損失関数とする
- あるアルゴリズムに従って局所解を見つける
@TODO イメージ図と式あとで書く
k-meansのアルゴリズム
分散を計算するので事前に標準化が必要
ランダムにクラスタを振り分けて、中心を求めて、その中心から近いデータを再度振り分け判定を繰り返す。
62 K(クラスタ数)の決め方
クラスタ数kの決め方
ドメイン知識やデータの背景から仮説を立てる、色々なkを試す
Elobow method
kを増やしていき、損失が球に下がったところのkを採用する
elbowにならないこともある
63 k-means
sklearn.cluster.KMeans
new KMeans
fit(X)
predict(X): 各データのクラスタリングの結果を参照
score(X): 損失を計算
k-meansの注意点
- 特徴量の数が多い(高次元空間)場合は二組のデータ間の距離に差がなくなってくるので、うまくクラスタリングができなくなる
-> 特徴量選択やPCAで次元削減するとよい - 質的変数との相性が悪い
- ダミー変数化して0,1,2..の距離を計算しても意味を持たない
- 高次元化してデータ感の距離に差がなくなっていく
-> 量的変数のみでk-meansをしたり、k-modes(最頻値)などの別のアルゴリズムを使用
66 階層クラスタリング
dendrogram(樹状図)を作り階層的にクラスタリングする
アルゴリズムの流れ
0. データは事前に標準化
- 各データを各クラスタとする
- 距離が最も近いクラスタ同士を融合し一つのクラスタにする
- 2を繰り返す
- 最終的にクラスが一つになるまで
クラスタ間の距離の図り方
single: クラスタ感で最も近いデータの距離
complete: クラスタ間で最も遠いデータの距離
average: クラスタ間の全ての二組のデータの距離の平均
centroid: 各クラスタの中心間の距離(inversionが起きないようにする必要がある)
ward: クラスタ間の距離 = 全体の分散 - (各クラスタ内の分散の合計)
ward -> 各クラスタ内の分散の合計が小さいとクラスタ間の距離は大きくなるので、離れている。逆に合計が大きいと、値は小さくなるので、距離は小さいと考える(のだと思う)
類似度(距離)の定義
ユークリッド距離
マンハッタン距離
相関を使って類似度を測る
階層クラスタリングの注意点
ネストできないようなデータに対してもネスト型の階層を作ってしまう
性別、職業とあったら、男、女で分けるのが正しいが、女、医者で分けて、その下に男、弁護士のようなクラスタがある、のようなこと?
階層クラスタリングとDengrogramの描画
scipy.cluster.hierarchy.linkage: クラスタリング実施。dendrogramを構成する情報NumPyArrayで返す
scipy.cluster.hierarchy.dendrogram: dendrogramを描画
階層クラスタリングの結果の分布を描画する
scipy.cluster.hierarchy.fcluster
まとめ
クラスタリングは正解ラベルを必要としない教師なし学習
k-meansはクラスタ内の分散が最小になるようにk個のクラスタに分割する
階層クラスタリングはデータを近いもの順にクラスタリングしていく
セクション5 分類機の精度 指標
混同行列 Confusoin Matrix
sklearn.metrics.confusion_matrix
sklearn.metrics.ConfusionMatrixDisplay

Accuracy
sklearn.metrics.accuracy_score
Precision
sklearn.metrics.precision_score
陽性と判断したものは陽性であってほしい。(予測が間違ってたらPrecisionは低くなる)
Precisionを高くしたい場合は陽性と判断したものがとにかく間違ってないでいてほしい感じ?
自信のないものは偽物と判断するようにAIを設定すれば、適合率(precision)は高くなります。

また、本当に本物か怪しいものまで本物と判断するようにAIを設定すれば、適合率(precision)は低くなります。

Recall
sklearn.metrics.recall_score
陽性が極端に少ない場合の偏りのケースでも適切に評価できる場合がある
全て陽性に分類するようなモデルでは100%の精度が出てしまう
再現率(Recall)を高くするということは
自信のないものは本物と判断するようにAIを設定すれば、再現率(recall)は高くなります。
-> 陽性を取りこぼしたくない。陽性と予測してそれが結果陰性(FP)だったとしても多くを陽性としておいて、(要請がふるいに残る側だったとしたら)ふるいに残しておく。
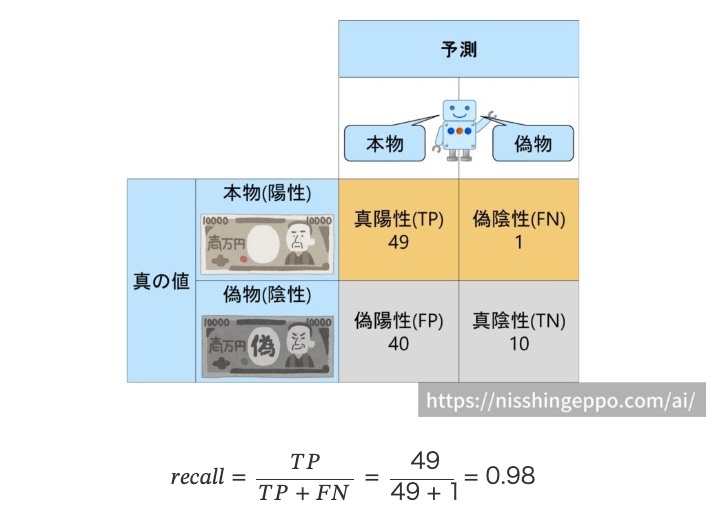
再現率(Recall)を低くするということは
また、本当に本物か怪しいものは偽物と判断するようにAIを設定すれば、再現率(recall)は低くなります。
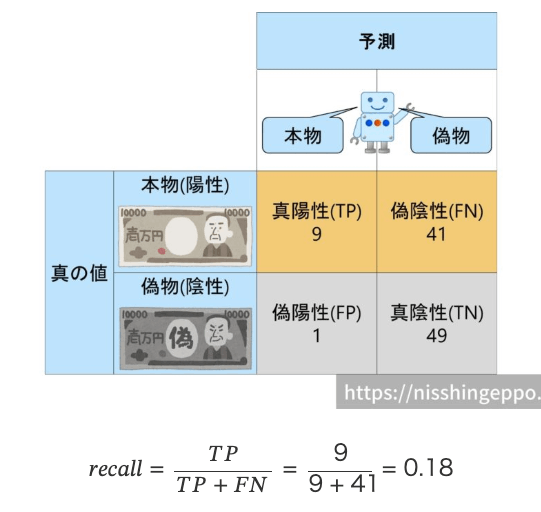
出所: https://nisshingeppo.com/ai/whats-recall/
Specificity
recall_score(np.array(y_true)!-1, np.array(t_pred)!-1)
多クラスでの評価指標の計算の仕方
多クラスの場合は大きく2つの計算の仕方がある
macro平均: クラスレベルで平均をとる
micro平均: データレベルで平均をとる

Accuracyは通常micro平均をとる
Precision、Recall、Specificityは通常macro平均をとる
Precision、Recall、Specificityのmicro平均はAccuracyと同じになる
sklean.metrics.precision_score(y_true, y_pred, average='macro|micro|None')
Noneを渡すとクラス別に指標を計算しlistで返す
確率の閾値による精度のコントロール
分類器は通常、確率の閾値によって分類ラベルを決定する
閾値の調整によりそれぞれの精度指標(accuracy、precision、recall、specificity)をコントロールすることができる
PrecisionとRecallのトレードオフ
PrecisionとRecallはトレードオフの関係がある
Precisoin-Recall Curve
precision, recall, threshhold = sklearn.metrics.precisoin_recall_curve(y_test, y_pred_probal[:, 1])
F値(F-Score, F1-Score)
PrecisionとRecallの調和平均を取った値
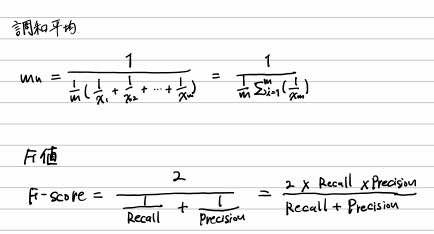
F値
sklearn.metrics.f1_score
f1_score(y_true, y_pred)
調和平均
scipy.stats.hmean
hmean([recall_score(y_true, y_pred), precision_score(y_true, y_pred)])
図にあるようなF値の最も高い値を探す
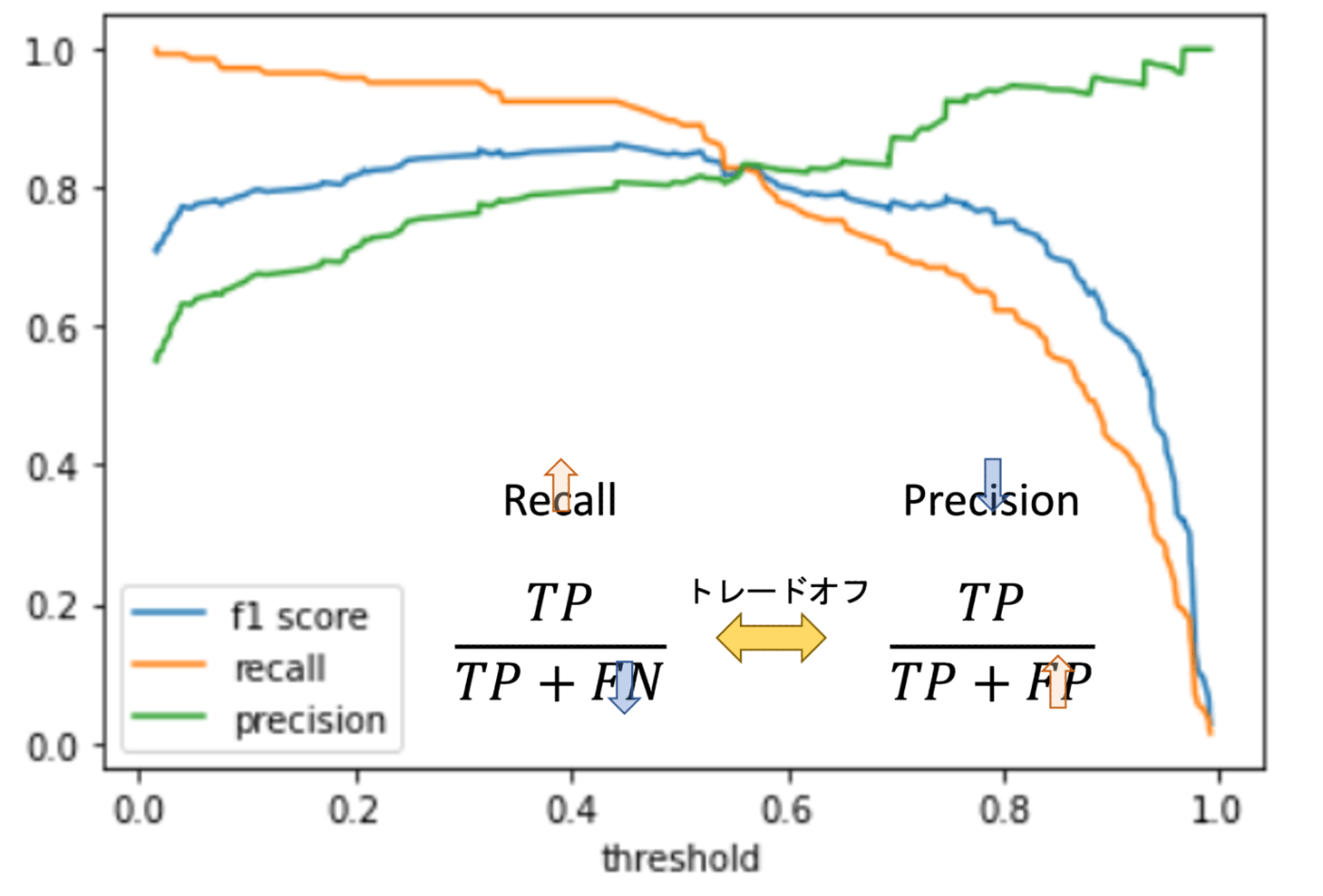
出所: https://datawokagaku.com/f1score/
scikit-learnにおける2値分類でpredictをするとデフォルトの閾値0.5で分類されるのをthresholdの値を使って分類する例
ROC
Receiver Operating Charactaristic
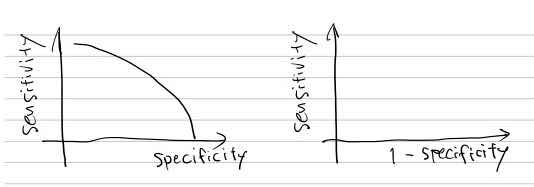
- Sensitivity(Recall)とSpecificityはトレードオフの関係にある
- 横軸 1 - Specificity、縦軸Sensitivityとして時に閾値の変化が描くカーブ
参考
Sensitivityは、陽性のデータに対して、陽性と分類できた割合 -> TPR: True Positive Rate
1 - Specifictyは、陰性のデーたに対して、間違えて陽性に分類 した割合 -> FPR: False Positive Rate

Sensitivityを上げるために陽性と分類する頻度を上げると、陰性データを間違えて陽性と分類する頻度も上がり1-specificityも上がってしまう。
sklearn.metris.roc_curve
fpr, tpr, threshhold = roc_curve(y_test, y_pred_probal[:, 1])
AUC(Area Under the Curve)
- ROCにおける精度を数値化したもの
- ROCが作る面積
- 1が最大で、ランダムな分類器では0.5になる
sklearn.metris.auc
auc(fpr, tpr)
多クラス分類におけるROC
解説
線形補完
np.interp(補完したい値を含めた配列、data_x, data_y)
セクション3 ロジスティック回帰
分類タスク
- 目的変数が質的変数になる(回帰では目的変数が量的変数)
- 分類タスクでは、決定境界を作ってデータを分類することを目的とする
- 決定境界を引く機械学習モデルを分類器(classifier)という

出所: https://datawokagaku.com/logistic_reg/
他参考
分類アルゴリズム
- 目的変数を0 or 1の2値として扱う
- 回帰は予測値が0 ~ 1の範囲を超えてしまい解釈できないためそのまま使えない
- 多クラスの場合は0, 1 2...の様に単純に数値化して量的変数のようにすることはできない
- 回帰を使うと外れ値一つで大きく結果が変わってしまう
ロジスティック回帰
- 回帰という名前が付いているが分類のアルゴリズム
シグモイド関数(ロジスティック関数)

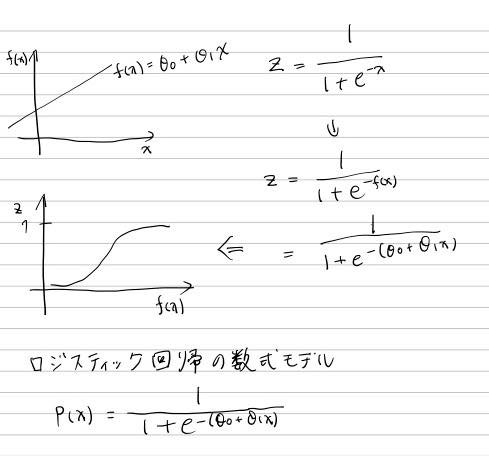
シグモイド関数のxに線形回帰の式を割り当てるからロジスティック「回帰」という、回帰という文字がこのアルゴリズムの名前に入っている。
pはprobability。確率。
ロジスティック回帰の損失関数
𝜃(特徴量係数)を求めるための損失関数が必要
最小二乗法では複雑になってしまうので使ってはいけないとのこと
LogLoss(交差エントロピー(crossentropy))を使用
解説・参考
python ロジスティック回帰
sklearn.linear_model.LogisAcRegression
.predict(X)でラベル(クラス)の分類結果を取得
.predict_proba(X)でラベル(クラス)の確率𝑝(𝑋)を取得
sklearn.metrics.log_loss
4 多クラス分類のロジスティック回帰
2値分類ではロジスティック回帰が利用できるが、多クラス分類ではそのままロジスティック回帰を利用することはできないとのこと。
主に利用できる手法は以下2つ。
- One vs Rest (OvR)
- 多項ロジスティック回帰 (Mul3nomial logis3c regression)
One vs Rest (OvR, One vs All)
クラスの数だけ分類器を作り最も確率が高いクラスを最終的な分類結果とする
多項ロジスティック回帰(Multinomial logistic regression)
2値分類用の損失関数を多クラス対応させたもの
一度の学習で多クラスに対応するモデルを構築可能
方法としては
- 目的変数のエンコーディング(one-hotエンコーディングを行う)
- シグモイド関数 -> ソフトマックス関数
- 損失関数の多クラス対応
ソフトマックス関数
ソフトマックス関数はシグモイド関数を一般化したもの
正直ここで紹介された式はここだけの説明だけではあまりイメージがわかない。他の教材にあたるべき。
多項ロジスティック回帰 の損失関数
セクション 8 決定木
領域の分割の仕方(回帰)
分割後の二つの領域の残差(偏差)の平方和の合計が最小になるように二分していく
領域の分割の仕方(分類)
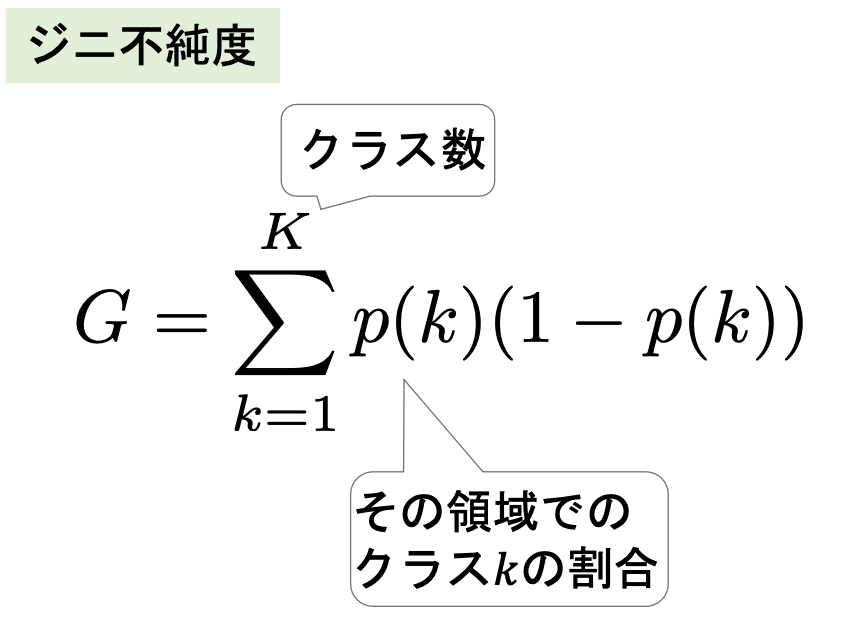
ジニ不純度(gini impurity)
分割後の二つの領域のジニ不純度の合計が最小になるように二分していく
ジニ不純度: どれだけ綺麗に分けれるかを表す指標 -> どれだけ「不純なもの」が含まれるか
決定木の剪定(pruning)
過学習を防ぐため,一部の木(枝)を取り除く(剪定する(prune))
葉の数だけペナルティを与えるcost complexity pruning
決定木モデルを構築する
決定木(回帰)
sklearn.tree.DecisionTreeRegressor
決定木(分類)
sklearn.tree.DecisionTreeClassifier
決定木モデルを可視化する
決定木の可視化(描画)
sklearn.tree.plot_tree
決定木の可視化(テキスト)
sklearn.tree.export_text
決定木の特徴量の重要度を描画
feature_importances_
feature_names_
Minimal cost complexity pruning
.cost_complexity_pruning_path(X, y)で,と𝛼と不純度をリストで取得する
それぞれの𝛼でのモデルの精度を計測し,最良の𝛼を使用する
9 SVM(Support Vector Machine)
あるデータがサポートとなり,そこからの距離(マージン)が最大化するように決定境界をひく
距離を使うので事前にSVMでは標準化することが望ましい
SVMの損失関数
マージンを最大化しつつ誤分類を減らす
⭐
カーネルトリック
⭐
SVMを構築する
⭐
sklearn.svm.SVC
回帰はsklearn.svm.SVR
決定境界とサポートベクトルを可視化する
sklearn.inspecAon.DecisionBoundaryDisplay