最短コースでわかる、ティープラーニングの数学読書メモ
1 機械学習入門
1.3 はじめての機械学習モデル
標本点ことに正解値ytと予測値ypの差の2乗を計算し、すべての標本点での合計を損失関数として評価する
この考えが「残差平方和」と呼ばれ、線形回帰モデルでの標準的な損失関数の考え方になっています
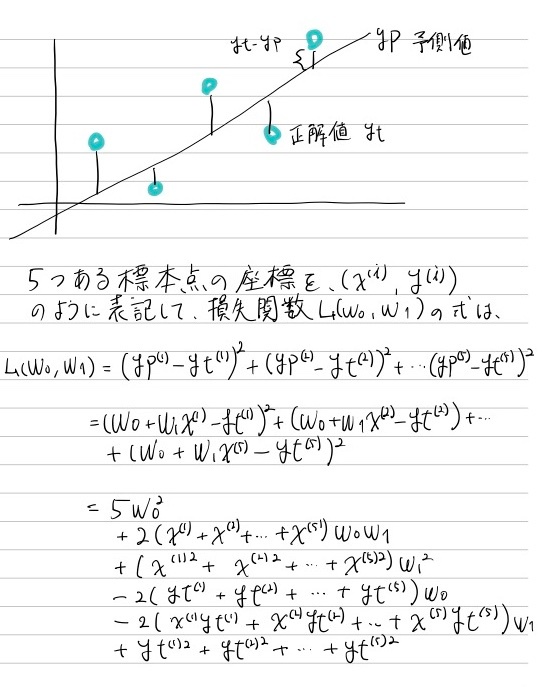
具体的な値を与えてみて計算
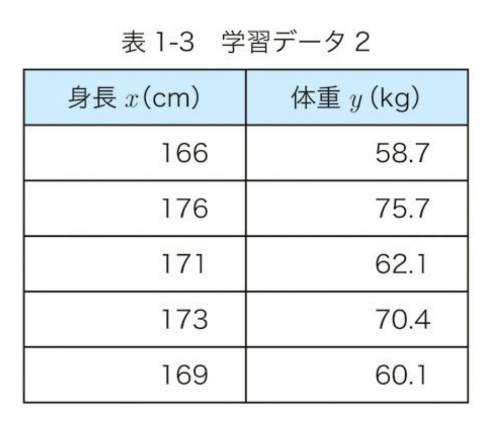
xとyのそれぞれの平均で引く
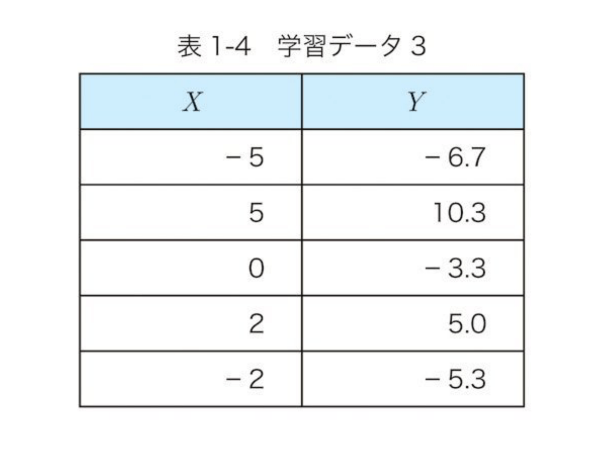


2 微分積分
2.2 合成関数・逆関数
合成関数
2つの関数f(x)とg(x)があるとします。この時、f(x)の出力をg(x)の入力とすることにより、2つの関数を組み合わせた新しい関数を作る個が可能です。こうして作られた関数のことを合成関数といいます。
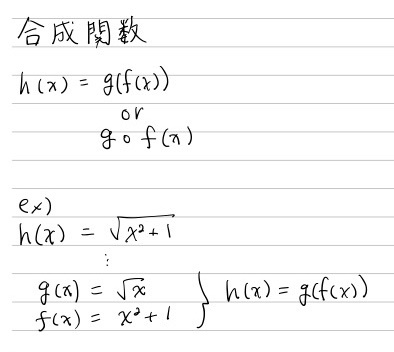
逆関数
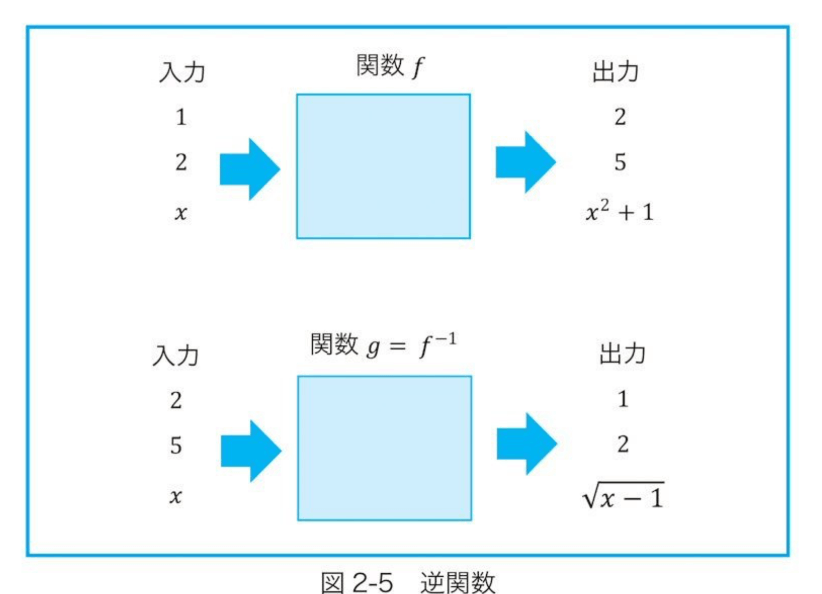
書籍引用
逆関数の特徴として、関数y=f(x)のグラフと逆関数y=g(x)のグラフはy=xの直線に関してちょうど対象な図形となる
解説記事
2.3 微分と極限
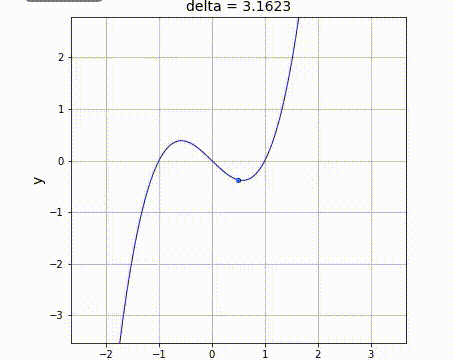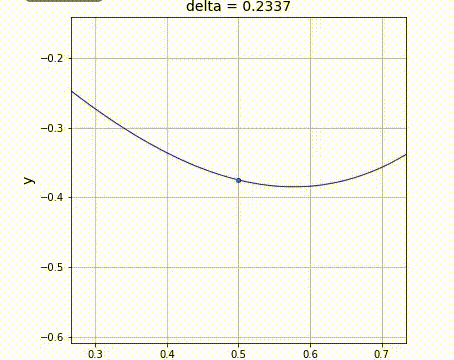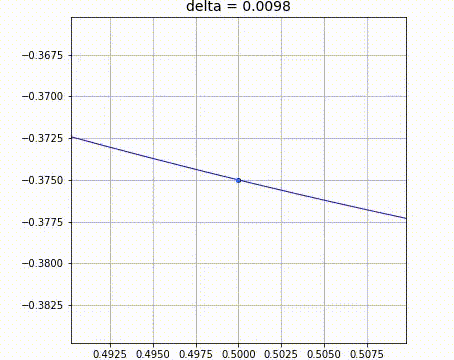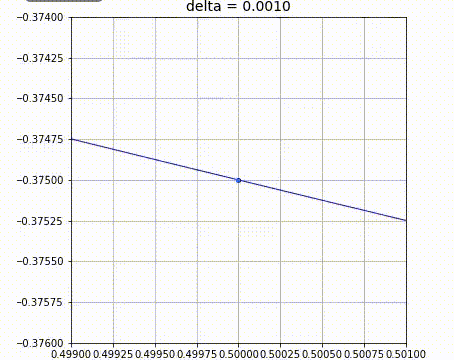
出所: https://github.com/makaishi2/math-sample/blob/master/movie/diff.gif
微分とは結局「xを少しだけ増やしたときの、yの増える量を比で表したもの」

2.3.2 微分と関数値の近似表現
ここの説明よく分からなかった。
2.3.3 接線の方程式

ここのコラムにてx, yを与えてy=ax+bとなる方程式を求めて、aの値を決定するフェーズを学習フェーズ。そのaを使ってyを予測することを予測フェーズに当てはめた解説をしていた。
2.4 最大、最小
関数f(x)の微分f'(x)の値が0になるようなxの値で、関数は最大または最小の値をとる
(とらない場合もある。例y=x³のグラフ)
2.5 多項式の微分
2.5.2 微分計算の線形性と多項式の微分

微分演算の他に「線形性」の成り立つ例としては、原点を通る一次関数(線形の名前の由来)やベクトル間の演算だる内積などがあります
コラムC(Combination)と二項定理
解説
2.6 積の微分
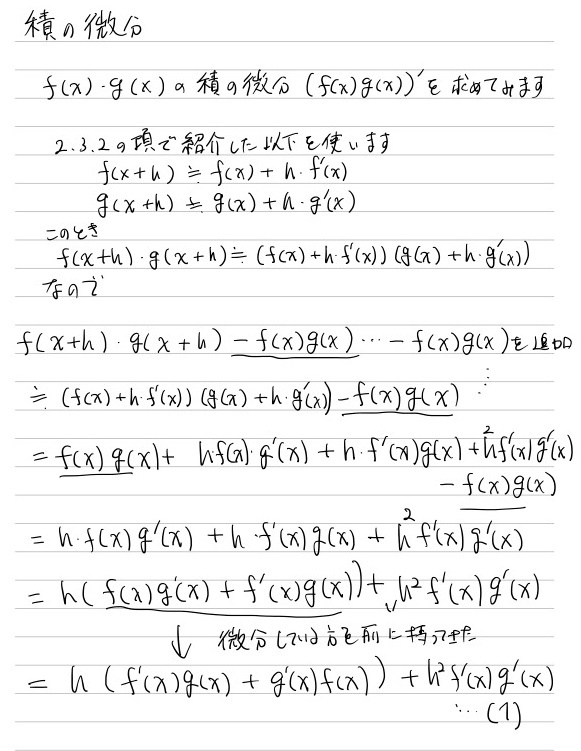
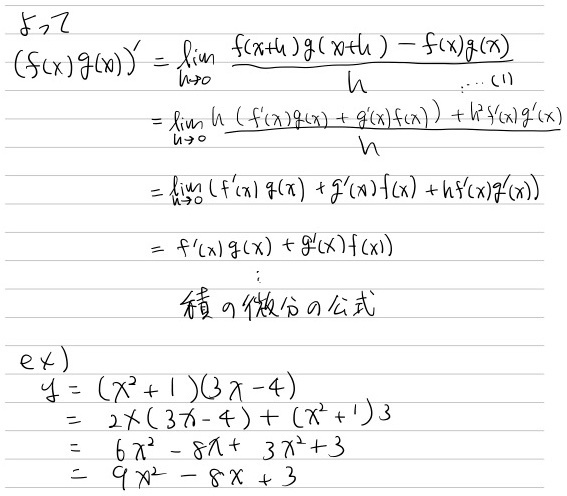
2.7 合成関数の微分

2.7.2 逆関数の微分

参考
2.8 商の微分


参考
29 積分
S(x + dx) - S(x) ≒ f(x)dx + 1/2f'(x)(dx)² の2乗の部分が分からないなぁ
3 ベクトル・行列
3.3 ベクトルの長さ
3.3.3 ベクトル間の距離

3.4 三角関数

3.5 内積


3.6 コサイン類似度

問題は「4次元以上のときの2つのベクトルのなす角度とは何か」です。...そもそもなんであるかもイメージできないわけです。
しかし、次元が100次元であっても、この式でコサインっぽいものが出せることは確かで、少なともこの式で求めた値が1に近い場合、「2つのベクトルの向きは近い」ということがいえそうです。
そこで、多次元ベクトルを対象に上のcosθの値に該当する計算をした場合、その値をコサイン類似度と呼びます。
コサイン類似度は、ベクトル間の向きの近さを示す指標として実際によく使われています。
コラムに使用例が紹介されている。
3.7 行列と行列演算

4 多変数関数の微分
4.2 偏微分
複数ある変数のうち、1つの変数だけが変化するものとして、残りの変数を定数とみなす方法が考えられました。これが偏微分と呼ばれる
4.3 全微分

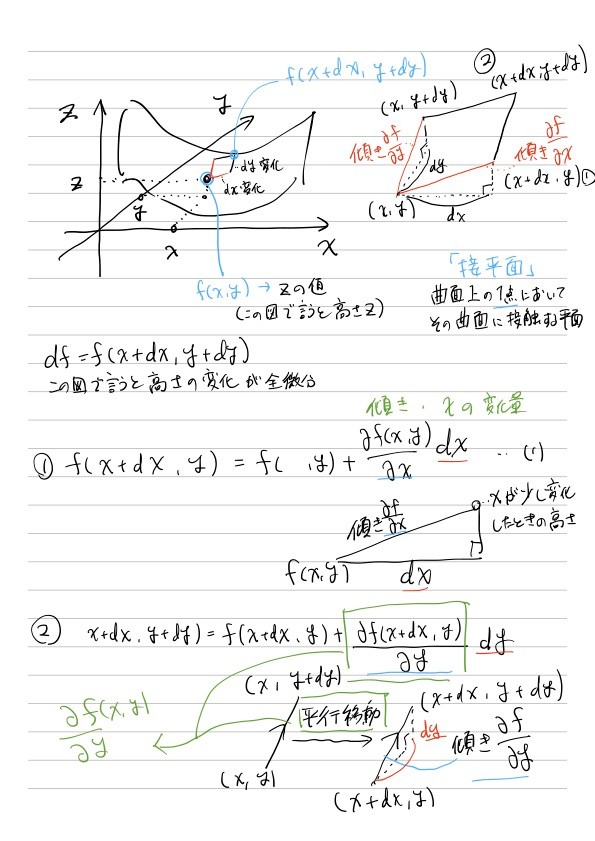

参考
4.4 全微分と合成関数


公式だけ記載。証明の過程は理解できなかったので未記載。
参考
4.5 勾配降下法
ある2変数関数 L(u, v)が与えられたとき、L(u, v)の値を最小にするような(u, v)の値(min u, min v)を求めたい


勾配降下法で移動量を出す計算は損失関数の偏微分の計算であることもわかったと思います。機械学習・ティープラーニングにおける繰り返し計算の本質は損失関数の微分なのです。
勾配降下法の様子を示すアニメーション
参考
5 指数関数・対数関数
5.1 指数関数


5.2 対数関数

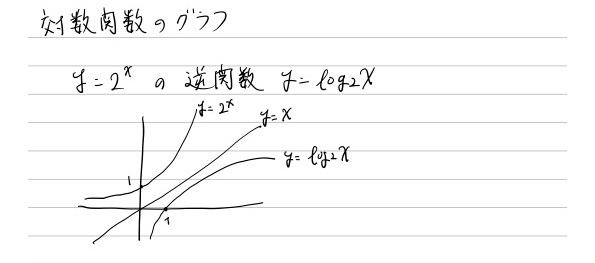
逆関数のグラフと元の関数のグラフはy=xに関して対象な関係にあります。
対数関数は正の値に対してしか定義されないことがあります。
これは逆関数である指数関数が関数の値として正の値しかとらないことと対応しています。
仮数f(x)に対してxのとりうる値の範囲を定義域、f(x)のとりうる値の範囲を値域といいますが、
指数関数の値域は正の範囲
対数関数の定義域は正の範囲
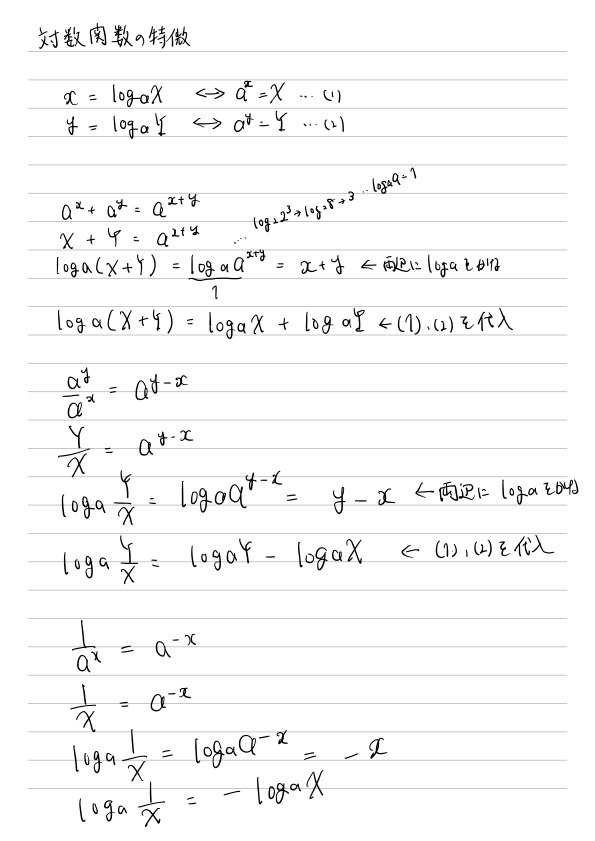
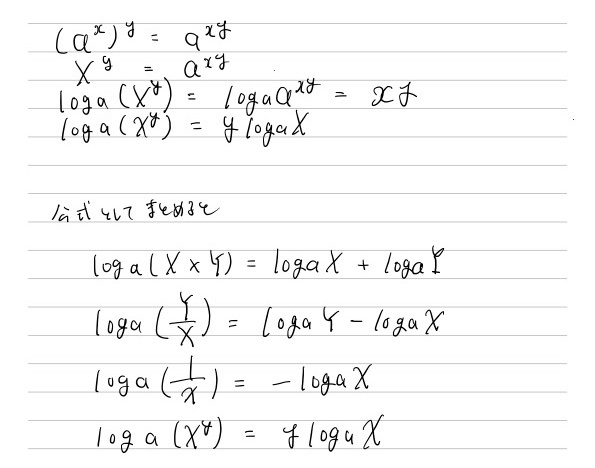
5.3 対数関数の微分


参考
5.4 指数関数の微分


参考
5.5 シグモイド関数


5.6 softmax関数


参考
6 確率・統計
6.1 確率変数と確率分布
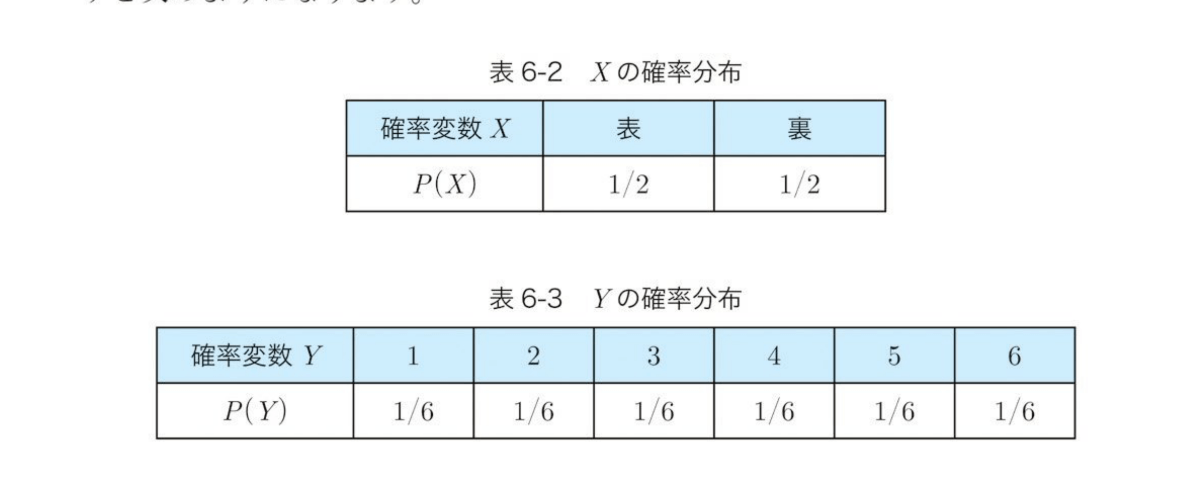
確率変数のとりうるそれぞれの値について、確率の値を表形式にまとめたものを確率分布といいます。
「1か0かの結果となる独立した試行n回行ったときに、1の結果が出た回数」を確率変数とした場合の確率分布のことを、二項分布と呼びます
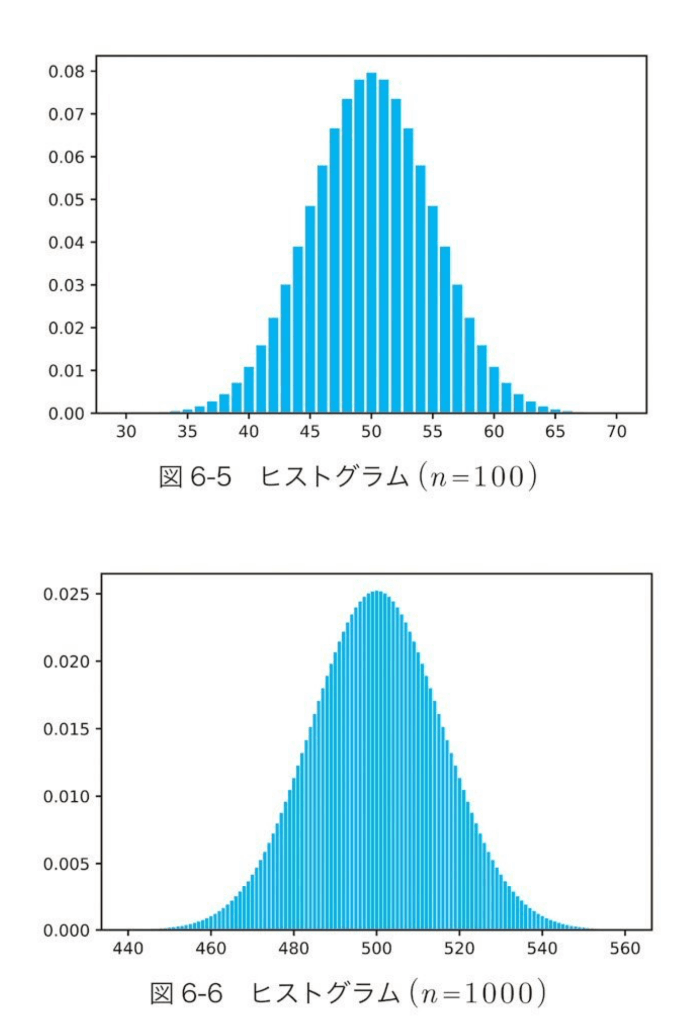
横軸は確率変数を、縦軸はそのときの確率密度を表す。
6.2 確率密度関数と確率分布関数
二項分布のヒストグラムはnの値を大きくしていくと、ある連続関数に近づいていきます。この関数は、次の式で表されるものであることがわかっており、正規分布関数という名前がついています。
また、二項分布関数が正規分布関数に近づいていく性質は、中心極限定理と呼ばれています。
確率変数が連続的な値を取る場合、確率は正規分布関数のような連続関数で考えることができます。この時の関数のことを確率密度関数と呼びます。

確率変数が連続値であるような事象では、実際の確率値を計算するには確率密度関数を積分した結果が必要になります。この計算で必要な確率密度関数の原始関数のことを、確率分布関数と呼びます
正規分布関数とシグモイド関数
実数値から確率値を出したい時に、変換用の関数に正規分布関数を使うのは自然の発送です。しかし機械学習モデルで確率値を出すのに利用されるのはシグモイド関数であって、通常、正規分布関数が使われることはありません。
その一番大きな理由は、確率密度関数が正規分布関数である場合に、その積分結果(確率分布関数)が解析的に解けない(関数式として表すことができない)ことがあげられます。

さらにシグモイド関数と、正規分布関数はグラフの形も大変似ています。
書籍グラフ参照
6.3 尤度関数と最尤推定
最尤推定
母数θを変数とみたしたとき、尤度L(θ)が最大となる母数θを母数の推定量として採用する方法
解説
最尤推定の手順
- 尤度関数を求める
- 尤度を最大にする母数を求める
尤度L(P)が最大になるpは、L(P)を微分して0になるPのうちの一つ。
7 線形回帰モデル(回帰)
勾配降下法の公式
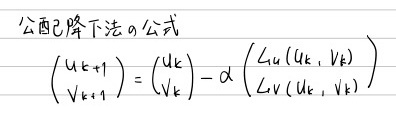
単回帰モデルの公式

7.6 損失関数の作成

データ数に関係なくするためデータ件数で割る、
また勾配降下法の準備のため損失の関数の微分計算をするのですが、元の式が2乗の式であるため、微分すると係数として2が出てきます。この2を打ち消すよう、最初から2で割った式を損失関数としておきます。
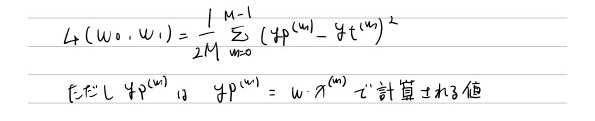
7.7 損失関数の微分計算


7.8 勾配降下法の適用

7.9 プログラム実装
なぜx.Tで計算するかの解説はありがたかった
列と列のデータの内積をとりかたかったので、片方を転置して意図したベクトル要素で内積をとる
7.10 重回帰モデルへの拡張

8 ロジスティック回帰(2値分類)
8.2 回帰モデルと分類モデルの違い
会期と分類
回帰の時は入力データ(x)と出力データ(y)の関係を示す直線であり、直線対処のすべてをいかにその直線に近づけるかが目的でした。
これに対して分類では、入力データをグループ分けすることが目的で、直線はグループ分けのための境界線として使います。
8.3 予測モデルの検討
分類についても、...損失関数はパラメータで微分可能な関数、言いかえるとパラメータwの変化に伴い連続的に変化する関数である必要があります。損失関数は予測値と正解値から計算されるものなので、結論として
「予測値を計算する関数はパラメータwに関して連続的に変化する必要がある」
線形関数 u = w0 +w1x1 + w2x2 ...(1)
(1)の計算結果をある関数にかけることで確率値(0から1の範囲の値)に変換する。この確率値を予測値とする
ここのある関数に挙げられる例として、シグモイド関数がある。
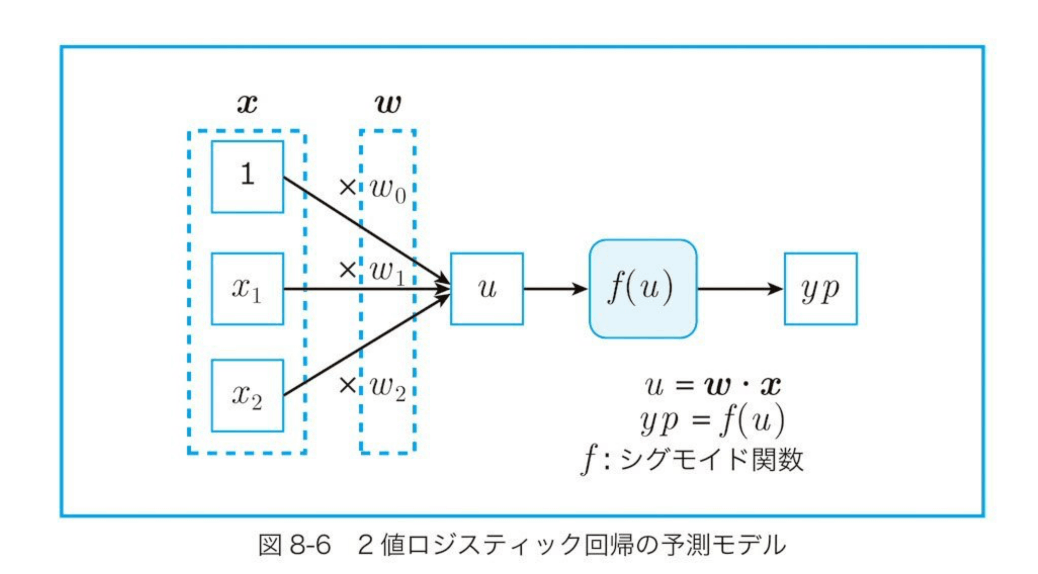
書籍引用
この図の流れになるまでの解説は書籍に解説されている

8.4 損失関数(交差エントロピー関数)
最尤推定により損失関数を定義
最尤推定のやり方は
予測値Pを「確率値」とみなす
この「確率値」を基に、個別の確率値の積として尤度関数を定義
尤度関数の対数をとった対数尤度関数を損失関数として定義
話を単純にするために、モデルの入力となるデータを5個にして考えてみる

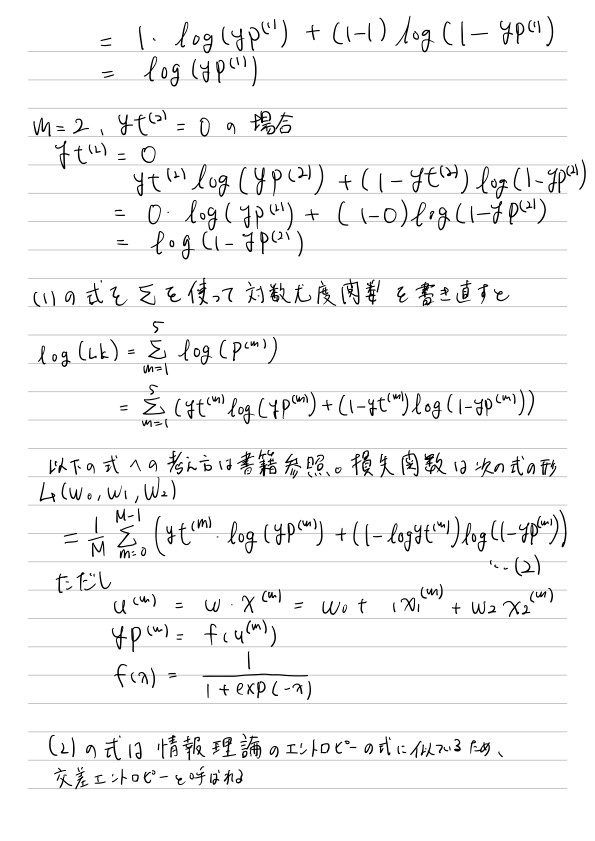

8.5 損失関数の微分


8.6 勾配降下法の適用

8.7 プログラム実装
線形回帰の場合、xとwの内積がそのまま予測値だったのに対して、ロジスティック回帰では内積の結果をシグモイド関数にかけて、その結果を予測として戻しています。
9 ロジスティック回帰モデル(多値分類)
多値分類は、
「oから1までの確率値を出力する複数の分類器を並列に作って、そして確率値の最も高い分類器に対応するモデルを全体としての予測値とする」というアプローチをとります
2値分類と比較して次の点が違います。逆に言うと2値分類モデルで2点を取り違えてしまえば、そのまま多値分類になるということです
重みベクトル -> 重み行列
シグモイド関数 -> sotmax関数
9.2 モデルの基礎概念
One Hot ベクトル
1対他分類器 One vs Rest Classifier
9.3 重み行列
2値分類時
u = w0 + w1x1 + w2x2
多値分類時(3値)
u0 = w00 + w01x1 + w02x2
u1 = w10 + w11x1 + w12x2
u2 = w20 + w21x1 + w22x2
重み行列Wと入力xとの内積
u = Wx
9.4 softmax関数
softmax関数の復習
- 入力: N次元ベクトル、出力: N次元ベクトルのベクトル値関数
- 個々の出力要素は0から1の値を取る
- すべての出力要素の値を足すと1になる

9.5 損失関数

9.6 損失関数の微分計算
9.7 勾配降下法の適用
9.8 プログラム実装
softmax関数の実装の箇所の
- オーバーフロー対策で最大値を引く工夫の意味がわからないなぁ
- 行列向けの計算の転置をしてまた転置をしてもとに戻す工夫の意味がわからないなぁ
10 ディープラーニング
@TODO 要復習