Zenn
🌊

どこをカットする？周波数特性から見る移動平均フィルタ

に公開
Python
信号処理
フィルタ
移動平均
tech

はじめに

私の持論ですが、移動平均は最も普及しているディジタルフィルタだと思います。
お手軽に波形を滑らかにしてくれるので、モノづくりの現場でも大いに活躍していますよね。

ですが、移動平均フィルタが周波数領域でどんな振る舞いをするか、特にサンプル数と波形の振幅変化の関係、つまり振幅特性については意外と知られていないようです。

そこで本記事では周波数領域で見た移動平均フィルタの振る舞いについて見ていこうと思います。

時間領域

まずは時間領域でのフィルタの動きを見てみましょう。

サンプリング周波数は1000Hzで、下記の通り元信号+ノイズの重畳した信号を作ります。
・元信号 => 5Hzの正弦波で最大振幅は±1.0
・ノイズ => 最大振幅が±0.8のホワイトノイズ

この信号に対してサンプル数10の移動平均フィルタをかけてみます。
結果は下記の通りです。

・ノイズ信号vsフィルタリング後信号

元の信号より、ちょっと滑らかになりますね。
元信号とも比較してみます。

・フィルタリング後信号vs元信号

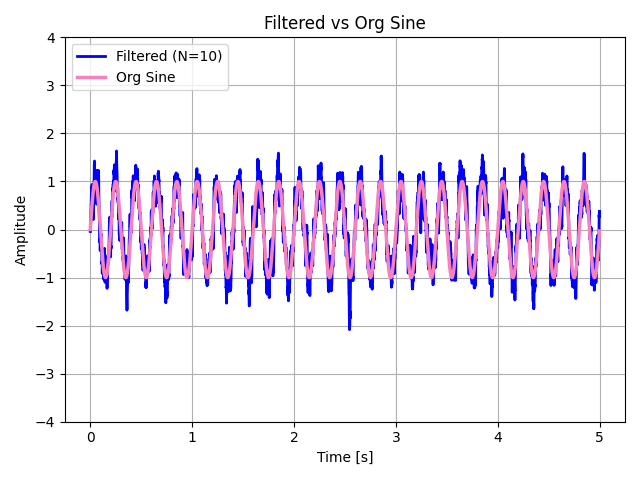
若干ノイズが残っている感じですが、時間領域での移動平均フィルタの動きとしては、全体的に
ノイズフロアを下げるような動作をしているように見える、というくらいでしょうか。

やはり時間領域での動作だけでは、フィルタの本質は分からないですね。(当たり前ですが)
では続いて、本題の周波数領域での動きを見ていきます。

周波数領域

サンプル数10の移動平均フィルタの周波数特性は下記の通りです。

・振幅特性

・位相特性

位相特性に関して、今回は単純移動平均なのでフィルタ係数は対称、すなわちこのフィルタは線形位相特性を持つということで良いと思います。

振幅特性の方はどうでしょうか？きっちり100Hzごとにノッチが出ていますね。
こうなる理由は、伝達関数から考えるとはっきり分かります。
それでは100Hzごとにノッチが出る理由を１ステップずつ導いてみましょう。

サンプル数10の単純移動平均FIRフィルタの伝達関数は下記になります。

H(z) = \frac{1}{10}\cdot(1+z^{-1}+z^{-2}+...+z^{-9}) = \frac{1}{10}\cdot\sum_{n=0}^{9}z^{-n}

伝達関数の右辺は\frac{1}{10}を除くと初項1、公比z^{-1}の等比数列の和なので、
下記のように書けますね。

H(z) = \frac{1}{10}\cdot\sum_{n=0}^{9}z^{-n} = \frac{1}{10}\cdot\frac{1-z^{-10}}{1-z^{-1}}

ここでz=e^{jω}と置くと、

H(e^{jω}) = \frac{1}{10}\cdot\frac{1-e^{-j10ω}}{1-e^{-jω}} = \frac{1-e^{-j10ω}}{10\cdot(1-e^{-jω})}

これで伝達関数が角周波数ωを含む形になりますね。

振幅特性におけるノッチは振幅が0になる周波数なので、上記伝達関数の分子である1-e^{-j10ω}が0になる周波数、すなわち零点を求めればノッチの周波数が分かります。

1-e^{-j10ω} = 0から、e^{-j10ω} = 1なので、オイラーの公式より、

e^{-j10ω} = cos(10ω)-jsin(10ω) = 1

実部のみ見ると、cos(10ω) = 1から、10ω = 2πk (k = 1, 2, ...)となるため結局、

ω = \frac{2}{10}\cdotπ \cdot k = \frac{1}{5}\cdotπ \cdot k

と表せますね。今回、サンプリング周波数は1000Hzなので2π = 1000すなわち、π = 500ですね。
これを先程の式に代入して、

ω = 100\cdot k

0<ω<2πに限定すると、100\cdot k < 1000 なので、0<k<10　つまり、この移動平均フィルタは
・最初のノッチは100Hzで以降100Hzごとに900Hzまでノッチが等間隔に表れる すなわち、
・ノッチのできる周波数はサンプリング周波数(1000Hz)とサンプル数(10点)の商の定数倍
そしてここまでの導出から、
・移動平均フィルタのノッチは伝達関数の零点である
ということが分かります。

単位円上で零点の配置を確認してみると、ノッチの配置通り等間隔で円周上に零点が並びます。
・単位円上での零点配置

次にFFT結果も見てみましょう。100Hzの整数倍で振幅が大きく減衰しています。
・FFT結果比較

まとめ

本記事では伝達関数を元に、移動平均フィルタの周波数特性、特に振幅特性について考えてみました。
繰り返しになりますが、本記事の結論を下記に示します。

＜結論＞
・移動平均フィルタは等間隔にノッチが表れるような振幅特性を持つ
・ノッチは伝達関数の零点にあたる周波数に生じる
・ノッチの生じる周波数はサンプリング周波数とサンプル数の商の定数倍となる

なんとなく感覚でサンプル数を決めても、そこそこの効果が簡単に得られる移動平均フィルタですが、周波数特性を理解して使用することで、もっと効果的に使えるようになると思います。

皆さんのご参考になれば嬉しいです！

※今回使用したテスト信号の作成用のPythonスクリプトです。
　もし同様の信号を作って試したい方がおられたら、使ってみてください。
https://github.com/otter1602/Moving_Average_Sample

Discussion