【離散コサイン変換】Part3. 復元と補間をしっかりきっちり使い分ける
はじめに
前回の記事で、離散コサイン変換(DCT)とL1ノルム最小化を用いた、欠損データからの信号復元の基本的な考え方について見てきました。
欠損データをはっきりくっきり?復元する
結論としては、データの半分以上が欠損している場合でも、DCTとL1ノルム最小化によって元信号の良い近似を得られる場合があるという結果でしたね。
※25%観測データに対する近似

しかし同時に、前回見てきた信号復元の手法では最適化問題の定式化と求解という、結構面倒な手順を踏む必要があります。
※定式化した最適化問題
取得データに欠損や外れ値がある場合、最も一般的な対処法としては信号を補間する方法が挙げられます。線形にせよ、二次以上にせよ、信号を補間するのであれば最適化問題の定式化と求解という手順を踏まずとも、望むものにそれなりに近い形の信号が得られることが多いです。
それでは、信号復元はただ面倒な手順を踏むだけで実用に耐えない手法で、実用上は補間を用いれば十分なのでしょうか?
答えはもちろんノーです。
信号の補間自体が有用な手法であることは間違いないものの、そこには明らかに信号復元と比較した場合のメリット/デメリットがあります。
今回の記事では補間と信号復元の違いとそれぞれの長所/短所について見ていこうと思います。
まずは比較
早速、欠損のある信号に対する補間と信号復元それぞれの適用による違いを比較してみます。
元信号として、500サンプルで構成される10HzのSin波を作ります。
・元信号(10HzのSin波)
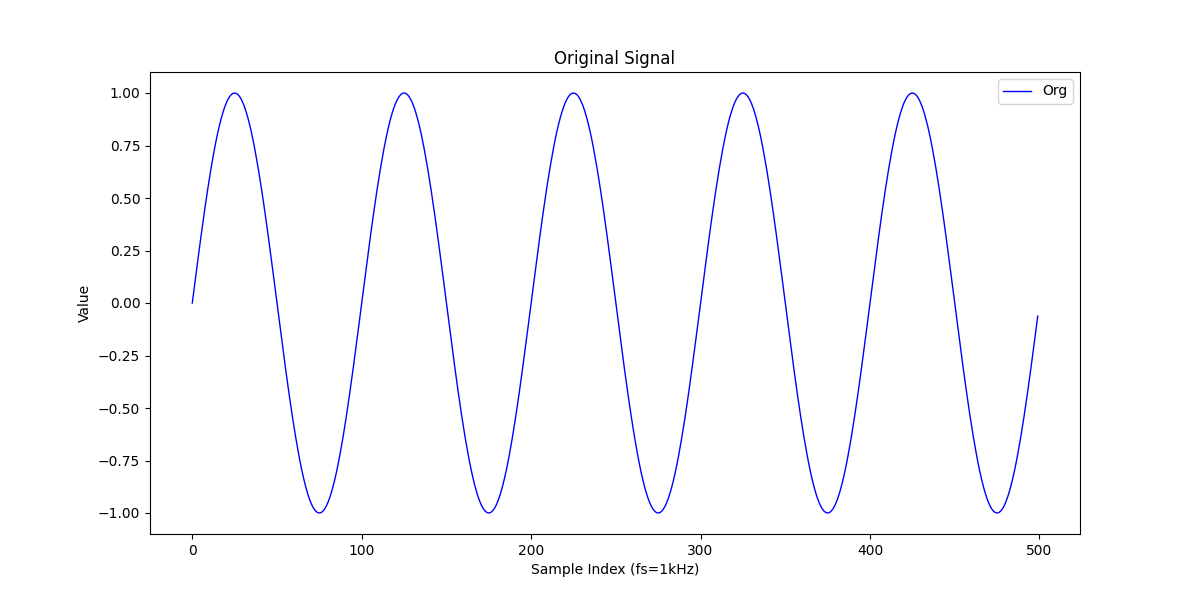
続いてこのSin波のうち、30%すなわち150サンプルをサンプリングします。
・元信号を30%サンプリング
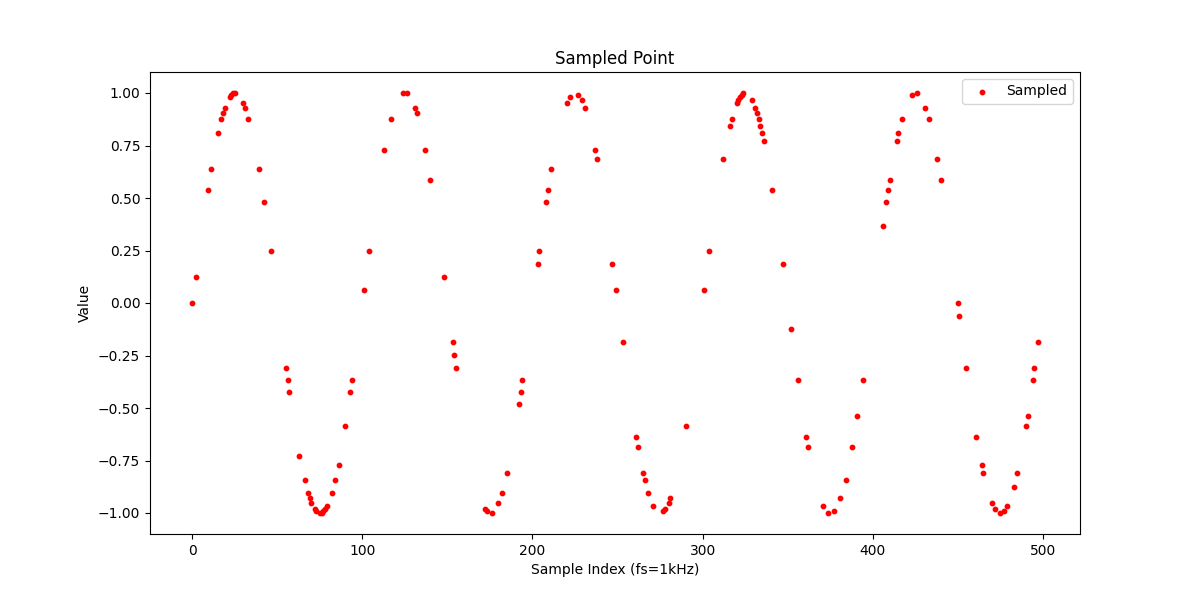
このサンプリング信号に対して信号復元、線形補間、3次のスプライン補間を適用した場合の信号を比較してみます。
・信号復元

・線形補間

・スプライン補間
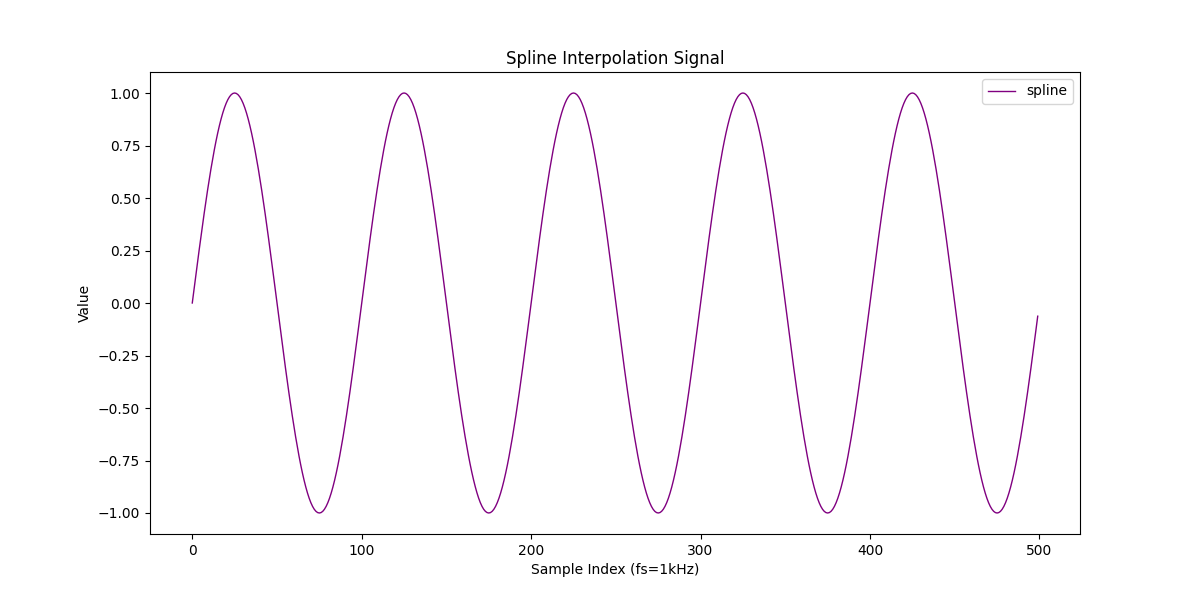
いずれの方法も元のSin波をかなり精度良く近似できているように見えますね。
MSEは信号復元/線形補間/スプライン補間でそれぞれ、0.000081/0.000270/0.000000です。
ここまでを見ると、信号復元のような面倒な手順を踏まなくても実用上は補間で十分と思われます。
では、次により実データに近くするため先程のSin波にガウスノイズを重畳させた信号を準備します。
・元信号(10HzのSin波)+ガウスノイズ

この信号を同様に30%サンプリングし、信号復元、線形補間、3次のスプライン補間を適用します。
・ノイズ有り信号を30%サンプリング
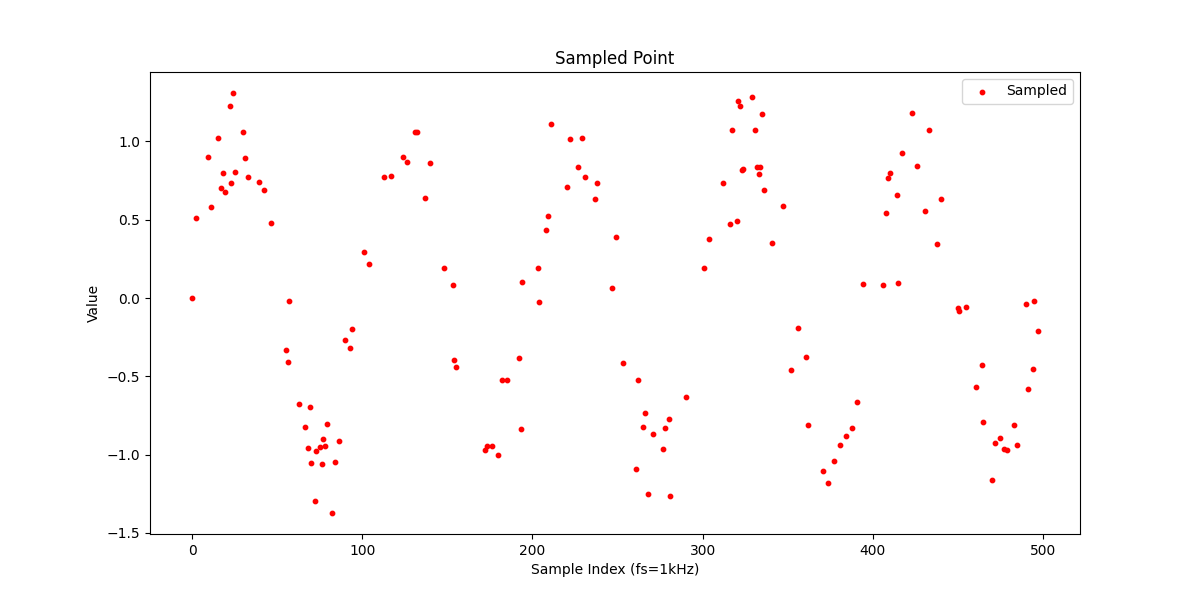
・信号復元

・線形補間

・スプライン補間

スプライン補間のみ最後のポイントで値が大きく下がっているため、縦軸のスケールが異なっていますが、いずれの方法でも何となく形状は近似できているように思われます。
MSEは信号復元/線形補間/スプライン補間でそれぞれ、0.058619/0.049865/0.203542です。
それではさらに条件を厳しくして、サンプリングを20%に減らして同様の処理を行ってみます。
・信号復元

・線形補間

・スプライン補間

どうでしょうか?線形補間とスプライン補間はかなり怪しい近似になってきています。
MSEは信号復元/線形補間/スプライン補間でそれぞれ、0.080885/0.070122/0.295126です。
同じグラフ上に並べるとより分かりやすいと思います。
・信号復元 vs 線形補間 vs スプライン補間
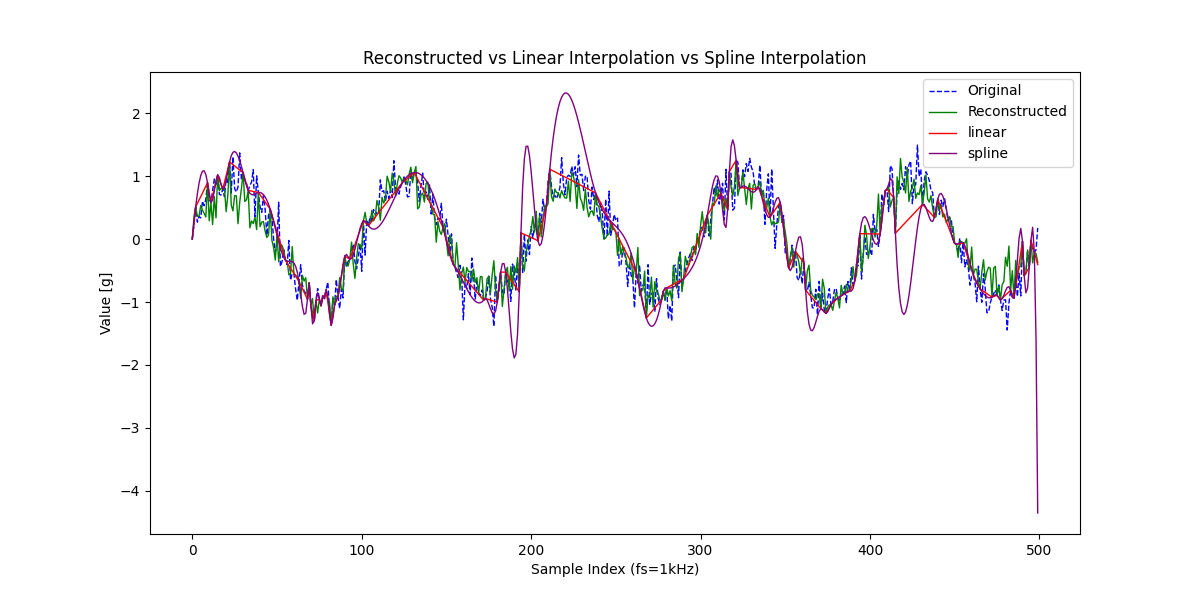
・信号復元 vs 線形補間

もはやスプライン補間は論外で、線形補間も信号の特徴を捉えているとは言い難いですね。
さて、ここまで信号復元と補間を比較してきましたが、傾向としては欠損率が低いほど、またノイズが小さいほど、信号復元と補間の差は無くなってくるように思われます。
逆を言えば、近似したい信号の欠損率が高く、ノイズが大きいほど近似の精度的には信号復元が補間を上回る可能性が大きいと言えます。
なぜそうなるのでしょう?この違いはどこから生じているのでしょうか?
補間と復元
信号復元と補間の違いがどこから生じているかを考えるにあたって、前節の例で用いた信号のサンプリングのグラフを再掲します。
・元信号を30%サンプリング

・ノイズ有り信号を30%サンプリング

・ノイズ有り信号を20%サンプリング

ここでちょっと考えてみてほしいんですが、例えばノイズ有り信号を30%サンプリングしたグラフと20%サンプリングしたグラフを比較すると、30%サンプリングしたグラフの方が何となく、サンプリング前の信号の形が分かりそうな気がしませんか?
感覚的な話ですが、これが補間の考え方そのものです。
どういうことかと言うと、補間は今あるサンプル点から、元々の信号の形を想像してすき間を埋めるということです。
そして想像して補う都合上、サンプル点の数が少ないほど想像で埋める範囲が広くなり、そしてノイズが大きいほど想像で埋めた範囲の精度が落ちるため、補間した結果は真の信号から離れる傾向があるということになります。
一方で信号復元の考え方は今あるサンプル点から、周波数領域で信号の特徴を求めて信号全体を近似すると言うことができます。
そのため、信号の特徴を捉えられるようなサンプルが取得できていれば、その数やノイズの大小はそれほど復元精度に影響しません。
よって信号が周波数領域でスパースである前提のもとでは、近似したい信号の欠損率が高くノイズが大きいほど真の値を表現する精度に関して、信号復元が補間を上回る可能性が大きいということになります。
メリット・デメリットと使い分け
<信号補間>
・メリット
実装が容易で、最適化問題の求解という面倒な手順を踏む必要がありません。
観測点の多いデータや、局所的な欠損の補完には非常に有用です。
・デメリット
欠損率が高い場合やノイズが大きい場合に、サンプリング点同士の値の差に敏感で
信号の全体的な形状を失いやすいです。
特に補間式の次数が大きいとノイズに過剰に反応する傾向があるため注意が必要です。
<信号復元>
・メリット
周波数領域で信号が持っているスパース性を活用することで、欠損率が高かったりノイズの影響が大きい
信号に関しても精度良く復元が可能です。
信号の主要な特徴を抽出・再構成する能力に優れています。
・デメリット
最適化問題の定式化と求解が必要であり、実装の難易度が高くなります。また、複雑で多くの周波数成分を似た大きさで含むような、スパースでない信号に対しては高い復元精度が期待できません。
<使い分け>
ものづくりの現場では、センサの故障や通信エラーによりデータに欠損が生じることや、周辺環境の変化によって突発的に大きなノイズや外れ値が生じることはよくあります。
そういった場合でも、信号復元によって信号のスパース性を利用すれば、よりロバストで精度の高い信号を得られる可能性があります。
一方で、現場で簡単にデータをキレイにして誰かに見せたいとき、また元々十分な精度で必要なデータ数が得られている場合は説明しやすく、分かりやすいデータを補間によって得ることもできます。
したがって、月並みなまとめになりますが、データの品質(欠損率とノイズ)と求めるもの(精度か容易さ)に応じて、各手法を使い分けることが実用上は最も重要であると言えます。
長くなったので、また次回の記事で信号のスパース性を応用した別の例について見ていきましょう。
Discussion