Pythonで回帰分析(Coef × logP)を使った印象評価を可視化
📌はじめに
回帰分析ってよく聞きますが、
要するに「原因と結果の関係を数値で明らかにする手法」です。
回帰分析を使って、各パーツが印象にどれほど影響しているかを明らかにします。
📌調査内容と分析に使用する入力データ(架空の調査データです)
30人の被験者に対して以下のような評価を実施しました。
(実際の調査では、数百人以上の被験者がいるほうが望ましいです)
📌目的
- どのパーツがどの印象にどのように影響しているかを明らかにする
- 特に印象を悪化させているパーツ(改善が必要な箇所)を特定する
1. イメージ評価(各車種ごと)
- 被験者に実際の A車・B車・C車 の3台を提示。
- 各車について、あらかじめ用意したイメージワードから、当てはまると思うものをすべて選択してもらいました。
- 複数回答可(MA: Multiple Answer)
- 該当するワードがなければ未回答も可能
- 回答結果を数値に変換
- 選択されたワード →
1 - 未選択 →
NaN
- 選択されたワード →
2. パーツ評価(各車種ごと)
- 各車について、「好きなパーツ」を2箇所、「嫌いなパーツ」を2箇所選択してもらいました
- 回答結果を数値に変換
- 好きなパーツ →
1 - 嫌いなパーツ →
-1 - 選択なし →
NaN
- 好きなパーツ →
3. 分析に使用するInputデータ
上記の回答結果が、分析に使用する sample_car_data.csv です。

| 列 | 内容 | 備考 |
|---|---|---|
| A | ID | 被験者ごとのユニークID |
| B | Car | 調査対象の車名 |
| C~K | 車に対するイメージワード(※以降 Trait) | 各列に異なるイメージ項目が入る |
| N~S | 車のパーツ名(※以降 Part) | 調査対象の車の各パーツ名 |
📌環境
python3.x
📌フォルダ構成
├─ 1_flow/
│ └─ part-trait-regression.py # 実行用スクリプト
├─ 2_data/
│ └─ area_image.csv # 入力データ
├─ 3_output/ # データ出力先(スクリプト実行時に自動作成)
📌コード解説(corres_analysis.py)
import os
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
from matplotlib.backends.backend_pdf import PdfPages
import matplotlib.colors as mcolors
# =========================
# ディレクトリ・ファイル設定
# =========================
INPUT_FOLDER = '2_data'
OUTPUT_FOLDER = '3_output'
parent_path = os.path.dirname(os.getcwd())
input_path = os.path.join(parent_path, INPUT_FOLDER, 'area_image.csv')
output_path = os.path.join(parent_path, OUTPUT_FOLDER)
os.makedirs(output_path, exist_ok=True)
save_name_1 = os.path.join(output_path, "1_分析条件を満たしたデータ.csv")
save_csv_radar = os.path.join(output_path, "2_回帰集計.csv")
save_csv_wide_all = os.path.join(output_path, "3_回帰結果_横長.csv")
save_pdf_he = os.path.join(output_path, "2_3_回帰結果_まとめ.pdf")
save_pdf_pl = os.path.join(output_path, "4_散布図と棒グラフまとめ.pdf")
save_pdf_re = os.path.join(output_path, "5_レーダーチャートまとめ.pdf")
# =========================
# 閾値
# =========================
threshold = 6
# =========================
# データ読み込み
# =========================
try:
df = pd.read_csv(input_path, encoding="utf-8")
except UnicodeDecodeError:
df = pd.read_csv(input_path, encoding="cp932")
1. 閾値の設定
-
threshold = 6は、1つのパーツやイメージが選択された回数の基準値です - この回数未満の場合、その項目は分析や処理から除外されます
- 今回は 選択数が6未満 の項目は分析対象外としています
# ==========================================
# 車毎に image_/area_ を閾値でフィルタ
# ==========================================
def filter_columns_by_car(df, prefix, threshold):
target_cols = [c for c in df.columns if c.startswith(prefix)]
filtered_dfs = {}
for car in df['Car'].unique():
df_car = df[df['Car'] == car]
counts = df_car[target_cols].apply(lambda col: col.isin([1, -1]).sum())
keep_cols = counts[counts >= threshold].index.tolist()
filtered_dfs[car] = df_car[['ID', 'Car'] + keep_cols]
return filtered_dfs
df_image_filtered = filter_columns_by_car(df, "image_", threshold)
df_area_filtered = filter_columns_by_car(df, "area_", threshold)
df_filtered_by_car = {car: pd.merge(df_image_filtered[car], df_area_filtered[car], on=['ID', 'Car'])
for car in df['Car'].unique()}
df_all = pd.concat(df_filtered_by_car.values(), ignore_index=True)
df_all.to_csv(save_name_1, index=False, encoding="utf-8-sig")
2. 車ごとに image_/area_ を閾値でフィルタ
- 閾値
threshold = 6未満のイメージやパーツはデータから除外します -
filter_columns_by_car関数の処理内容:-
image_またはarea_で始まる列を見つける - 車ごとに、
1(好き)や-1(嫌い)のカウント数が6以上の列だけを残す
-
❓ なぜ除外するの?
選択数が少ない(例:2件など)場合、偶然や外れ値の影響を受けやすく、
分析結果が偏ったりノイズの原因となる可能性が高いためです。
# =========================
# 回帰分析
# =========================
trait_cols = [c for c in df_all.columns if c.startswith("image_")]
area_cols = [c for c in df_all.columns if c.startswith("area_")]
trait_cols_clean = [c.replace("image_", "") for c in trait_cols]
area_cols_clean = [c.replace("area_", "") for c in area_cols]
all_results, all_pvalues = [], []
for car in df_all['Car'].unique():
df_car = df_all[df_all['Car'] == car].copy()
trait_result = pd.DataFrame(index=trait_cols_clean, columns=area_cols_clean)
trait_pvalues = pd.DataFrame(index=trait_cols_clean, columns=area_cols_clean)
counts = {}
for trait_orig, trait_clean in zip(trait_cols, trait_cols_clean):
y = df_car[trait_orig].fillna(0)
X = df_car[area_cols].fillna(0)
counts[trait_clean] = (y != 0).sum()
if y.nunique() <= 1:
trait_result.loc[trait_clean] = [0] * len(area_cols_clean)
trait_pvalues.loc[trait_clean] = [np.nan] * len(area_cols_clean)
continue
X_scaled = StandardScaler().fit_transform(X)
X_sm = sm.add_constant(X_scaled)
results_sm = sm.OLS(y, X_sm).fit()
trait_result.loc[trait_clean] = np.round(results_sm.params[1:].values, 3)
trait_pvalues.loc[trait_clean] = np.round(results_sm.pvalues[1:].values, 3)
trait_result.insert(0, "Count", pd.Series(counts))
trait_pvalues.insert(0, "Count", pd.Series(counts))
trait_result = trait_result.sort_values(by="Count", ascending=False)
trait_pvalues = trait_pvalues.loc[trait_result.index]
trait_result["Car"] = car
trait_pvalues["Car"] = car
trait_result = trait_result.reset_index().rename(columns={"index": "Trait"})
trait_pvalues = trait_pvalues.reset_index().rename(columns={"index": "Trait"})
all_results.append(trait_result)
all_pvalues.append(trait_pvalues)
final_result = pd.concat(all_results, ignore_index=True)
final_pvalues = pd.concat(all_pvalues, ignore_index=True)
final_result = final_result[final_result['Count'] > 0].reset_index(drop=True)
final_pvalues = final_pvalues[final_pvalues['Count'] > 0].reset_index(drop=True)
3. 回帰分析
各車ごとに、イメージ指標(image_ 列) を目的変数、
パーツ(area_ 列) を説明変数として、通常の最小二乗回帰(OLS)を実施します。
処理の流れ
- 列名から接頭辞
image_/area_を取り除き、表示用ラベルを作成 - 車ごとにループ処理
- 各イメージ指標(Trait)を
目的変数 y、各パーツを説明変数 Xとして回帰を実行 - 欠損値は回帰できないため便宜的に
0で埋める(=「影響なし」と仮定) - 目的変数
yが定数(例:全員0)の場合は回帰をスキップ - 説明変数
Xは標準化(StandardScaler)してから回帰
→ スケールの違いを調整するため - 定数項(切片)も計算されますが、保存するのは各パーツ列のみ
- 回帰係数・p値は小数点3桁に丸めて
DataFrameに格納
- 各イメージ指標(Trait)を
- 目的変数が非ゼロとなったサンプル数を
Countとして追加 -
Countが多い順に並び替え - 全車の結果を結合し、
Count > 0のTraitのみを最終結果として残す
❓回帰係数・P値・logPとは❓
- 回帰係数 = 効果の大きさ
- P値 = その効果の信頼性
- logP = P値を見やすくしたもの
| 用語 | 意味 | ポイント |
|---|---|---|
| 回帰係数 | 変数が1増えると、結果がどっち向きにどれくらい変わるかを示す数字 | +なら増える方向、−なら減る方向 |
| P値 | この効果が本当にありそうか、それとも偶然かを確かめる確率 | 小さいほど「本物っぽい」 |
| logP | P値をわかりやすく変換したもの | 数字が大きいほど「有意性が高い」 |
# =========================
# 回帰係数・P値・logP
# =========================
all_radar_data = []
columns_radar = area_cols_clean
cars = df_all['Car'].unique()
for car in cars:
coefs = final_result[final_result['Car']==car].set_index('Trait')[columns_radar].astype(float)
pvals = final_pvalues[final_pvalues['Car']==car].set_index('Trait')[columns_radar].apply(pd.to_numeric, errors='coerce')
for trait in coefs.index:
for part in columns_radar:
all_radar_data.append({
"Trait": trait,
"Part": part,
"Coef": coefs.loc[trait, part],
"pvalue": pvals.loc[trait, part],
"Car": car
})
df_radar = pd.DataFrame(all_radar_data)
# p値を直感的に扱えるよう変換
df_radar["logP"] = -np.log10(df_radar["pvalue"].clip(lower=1e-10))
# --- 2_回帰集計.csv 保存 ---
df_radar.to_csv(save_csv_radar, index=False, encoding="utf-8-sig"
# ==========================================
# df_radar を横長に変換して Coef と logP をまとめる
# ==========================================
# --- Coef 横長 ---
df_coef_wide = df_radar.pivot_table(
index=["Car", "Trait"],
columns="Part",
values="Coef"
).reset_index()
# --- logP 横長 ---
df_logp_wide = df_radar.pivot_table(
index=["Car", "Trait"],
columns="Part",
values="logP"
).reset_index()
# --- Count 列を追加(Coef が 0 でない数をカウント) ---
counts = df_radar[df_radar["Coef"] != 0].groupby(["Car", "Trait"]).size().reset_index(name="Count")
# --- マージ ---
df_wide_all = pd.merge(df_coef_wide, df_logp_wide, on=["Car", "Trait"], suffixes=("_Coef", "_logP"))
df_wide_all = pd.merge(df_wide_all, counts, on=["Car", "Trait"], how="left")
# --- 列順を整理 ---
cols_order = ["Car", "Trait", "Count"] + [c for c in df_wide_all.columns if c not in ["Car", "Trait", "Count"]]
df_wide_all = df_wide_all[cols_order]
# --- 回帰結果_横長.csv 保存 ---
df_wide_all.to_csv(save_csv_wide_all, index=False, encoding="utf-8-sig")
df_wide_all.head()
4. 回帰係数・P値・logP
回帰分析の結果を、可視化で使いやすい形に整形します。
処理の流れ
-
final_result(回帰係数)とfinal_pvalues(p値)から、車ごとのデータを抽出 - 各 イメージワード(Trait) × パーツ(Part) × 車種(Car) の組み合わせごとに
-
Coef(回帰係数) -
pvalue(p値) -
Car(車種)
をロング形式に展開
-
-
pvalueを信頼性指標として扱いやすくするため、-log10(pvalue)をlogPとして算出- P値が 0 になるのを避けるため、下限を
1e-10に設定
- P値が 0 になるのを避けるため、下限を
- 縦持ちのマスター表(
df_radar)を作成し、CSV保存 -
df_radarを横持ちに変換して、Coef と logP をまとめたCSV も出力
❓logP の計算処理とは❓
# p値を直感的に扱えるよう変換
df_radar["logP"] = -np.log10(df_radar["pvalue"].clip(lower=1e-10))
-
pvalue列:回帰分析で出た P値(偶然の可能性)。小さいほど信頼性が高い -
clip(lower=1e-10):P値がゼロに近すぎる場合でも、ゼロ割りや無限大を防ぐ -
-np.log10(...):P値を「大きいほど有意性が高い」と直感的に見やすく変換する
数値例
- P = 0.05 → logP ≈ 1.3
- P = 0.01 → logP = 2
- P = 0.001 → logP = 3
👉 logP が大きいほど「信頼性が高い」 と直感的に読み取れます

2_回帰集計.csv
2_回帰集計.csv の解説
1. Coef(回帰係数)
- 各パーツが Trait(イメージワード)の評価に与える影響の大きさと方向を示します。
- 正の値 → Trait のイメージを強める方向に影響
- 負の値 → Trait のイメージを弱める方向に影響
- 数値の大きさは影響の大きさを示す
- 例:
- ホイール:-0.092 → Futuristic のイメージを少し下げる
- アッパーグリル:0.059 → Futuristic を少し上げる
- リアグリル:0.012 → ほとんど影響なし
2. pvalue(P値)
- 「この影響が偶然でないか」の確からしさを示す統計値
- 小さいほど「偶然ではない=信頼性が高い」
- 一般的に 0.05 以下は統計的に有意とされるが、ここでは傾向の目安として使用
- 例:
- ホイール:0.205 → 弱い傾向ありだが有意ではない
- アッパーグリル:0.417 → 偶然の可能性が高い
- リアグリル:0.875 → ほぼ影響なし
3. logP(-log10(P値))
- P値を直感的に扱いやすく変換した値
- 大きいほど信頼できる影響
- 計算例:
- P = 0.05 → logP ≈ 1.30
- P = 0.01 → logP = 2
- P = 0.001 → logP = 3
- 例:
- ホイール:0.688 → 信頼度は低め
- アッパーグリル:0.380 → 信頼できない
- リアグリル:0.058 → 信頼度ほぼゼロ
4. Coef と logP の関係
- Coef は「影響の方向と大きさ」、logP は「その影響の信頼度」を示す
- 実務的にはこの組み合わせで判断するのが効果的。
| Part | Coef | pvalue | logP | ポイント |
|---|---|---|---|---|
| ホイール | -0.092 | 0.205 | 0.688 | Futuristic感をやや下げるが信頼度低め |
| アッパーグリル | 0.059 | 0.417 | 0.380 | わずかに上げる傾向、ほぼ不確か |
| リアグリル | 0.012 | 0.875 | 0.058 | ほとんど影響なし、信頼度も低い |
5. 読み取り方表
| 状況 | 読み解き |
|---|---|
| Coef 大 & logP 小 | 見た目の効果は大きいけど偶然の可能性あり |
| Coef 小 & logP 大 | 小さいけど確実な効果 |
| Coef 大 & logP 大 | 効果が大きく確実 |
| Coef 小 & logP 小 | ほぼ影響なし |
💡 まとめ
- Coef が大きくても logP が小さい → 偶然の可能性あり
- logP が大きければ Coef が小さくても確実に影響していると判断可能
- Coef と logP をセットで見ることが重要

回帰結果_横長.csv
回帰結果_横長.csv の解説
各 Trait と Part ごとの 回帰係数(Coef) と有意性(-log10(P値 / logP))を
横長形式で整理した 回帰結果_横長.csv のイメージです。
-
Car:車種 -
Trait:評価項目(例:Futuristic, Sporty など) -
Count:その Trait に対して有効なサンプル数 - 各 Part 列:Trait ごとの回帰係数(Coef)
- 各 Part_logP 列:Trait ごとの
-log10(P値)(logP)
この形式にすることで、回帰係数(Coef)の大きさと**有意性(logP)**を一目で比較でき、
ヒートマップやレーダーチャート作成時の入力データとしてもそのまま利用可能です。
# =========================
# 共通設定
# =========================
exclude_cols = ["Car", "Trait", "Count"]
columns_to_plot = [c for c in final_result.columns if c not in exclude_cols]
cars = final_result["Car"].unique()
n_cars = len(cars)
# ====================================
# 回帰係数・-log10(P値)ヒートマップPDF
# ====================================
fig, axes = plt.subplots(2, n_cars, figsize=(12*n_cars, 16), squeeze=False)
for idx, car in enumerate(cars):
coefs = final_result[final_result['Car']==car].set_index('Trait')[columns_to_plot].astype(float)
sns.heatmap(coefs.T, annot=True, annot_kws={"size": 20}, cmap="coolwarm", center=0,
linewidths=0.5, cbar_kws={'label': '回帰係数'}, ax=axes[0, idx])
axes[0, idx].set_title(f"{car}:回帰係数", fontsize=14)
pvals = final_pvalues[final_pvalues['Car']==car].set_index('Trait')[columns_to_plot].apply(pd.to_numeric, errors='coerce')
log_pvals = -np.log10(pvals.clip(lower=1e-10))
sns.heatmap(log_pvals.T, annot=True, annot_kws={"size": 20}, cmap="YlGnBu",
linewidths=0.5, cbar_kws={'label': '-log10(P値)'}, ax=axes[1, idx])
axes[1, idx].set_title(f"{car}:-log10(P値)", fontsize=14)
plt.tight_layout()
plt.savefig(save_pdf_he, dpi=300, bbox_inches='tight')
plt.close()
5.共通設定
- ヒートマップ作成で使わない列を除外
exclude_cols = ["Car", "Trait", "Count"]
columns_to_plot = [c for c in final_result.columns if c not in exclude_cols]
- 車種リストと車種数を取得
cars = final_result["Car"].unique()
n_cars = len(cars)
6. 回帰係数(Coef)・-log10(P値)ヒートマップ PDF
回帰分析結果を可視化するため、回帰係数(Coef) と -log10(P値) を車ごとにヒートマップとして描画し、PDF に保存します。
処理の流れ
-
matplotlibのsubplotsで、車ごとに 2 行(上:Coef、下:logP)× N 車列の図を作成 - 車ごとにループ
-
回帰係数(Coef)を抽出してヒートマップ表示- 使用関数:
seaborn.heatmap - カラーマップ:
coolwarm(中心 0)
- 使用関数:
-
-log10(P値)(logP) を抽出しヒートマップ表示- カラーマップ:
YlGnBu
- カラーマップ:
-
- レイアウトを整え、PDF 保存
ヒートマップの意味
-
回帰係数(Coef)
- パーツが Trait に与える影響の大きさと方向
- 正 → Trait を増加させる方向
- 負 → Trait を減少させる方向
-
-log10(P値)(logP)
- 影響の信頼性を直感的に示す値
- 値が大きいほど「確からしさが高い」
- 例:P=0.05 → logP ≈ 1.3、P=0.01 → logP=2
💡 まとめ
- ヒートマップ PDF により、車ごとの Trait に対するパーツ影響と信頼性を一目で比較可能
- Coef と logP を組み合わせて読むことで、影響の方向・大きさ・信頼性 が視覚的に理解できる
グラフ例
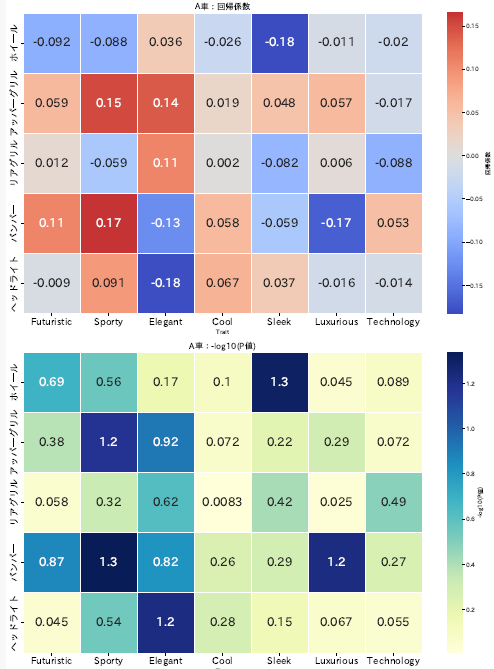
💡 Coef(効果の大きさ)と logP(信頼性)をセットで見ることが重要
- Coef が大きくても、logP が低いと「たまたまそう見えただけ」かもしれない
- Coef が小さくても、logP が高ければ「確実にその方向の効果がある」といえる
👉 解釈のポイント
- Coef が大きくても、logP が低いと「たまたま見えただけ」かもしれない
- Coef が小さくても、logP が高ければ「確実にその方向に影響している」といえる
# =========================
# 散布図・棒グラフPDF
# =========================
def prepare_data(car):
coefs = final_result[final_result['Car']==car].set_index('Trait')[columns_to_plot]
pvals = final_pvalues[final_pvalues['Car']==car].set_index('Trait')[columns_to_plot].apply(pd.to_numeric, errors='coerce')
log_pvals = -np.log10(pvals.clip(lower=1e-10))
df_coef_melt = coefs.reset_index().melt(id_vars='Trait', var_name='Part', value_name='Coef')
df_logp_melt = log_pvals.reset_index().melt(id_vars='Trait', var_name='Part', value_name='logP')
df_merge = pd.merge(df_coef_melt, df_logp_melt, on=['Trait', 'Part'])
df_merge['Label'] = df_merge['Trait'] + " × " + df_merge['Part']
df_merge['Car'] = car
return df_merge
all_data = [prepare_data(car) for car in cars]
with PdfPages(save_pdf_pl) as pdf:
fig, axes = plt.subplots(2, n_cars, figsize=(8*n_cars, 12), squeeze=False)
for idx, df_merge in enumerate(all_data):
car = df_merge['Car'].iloc[0]
# ---- 散布図 ----
ax = axes[0, idx]
# 正のCoefは赤、負のCoefは青、濃淡=logP
norm = mcolors.TwoSlopeNorm(vmin=df_merge['Coef'].min(),
vcenter=0,
vmax=df_merge['Coef'].max())
scatter = ax.scatter(df_merge["Coef"], df_merge["logP"],
c=df_merge["Coef"], cmap="RdBu_r", norm=norm, s=80, edgecolor='k')
ax.axhline(-np.log10(0.05), color='gray', linestyle='--')
ax.axvline(0, color='black', linewidth=1)
ax.set_xlabel("回帰係数", fontsize=12)
ax.set_ylabel("-log10(P値)", fontsize=12)
ax.set_title(f"{car}:パーツの影響と信頼性", fontsize=14)
for _, row in df_merge.iterrows():
ax.text(row["Coef"], row["logP"], f'{row["Part"]}\n({row["Trait"]})',
fontsize=10, ha='right')
# ---- 棒グラフ ----
ax = axes[1, idx]
# logP を 0-1 に正規化
norm_logp = df_merge['logP'] / df_merge['logP'].max()
# Coef の符号ごとに色を割り当て
colors_bar = [plt.cm.Reds(v) if c > 0 else plt.cm.Blues(v) for c, v in zip(df_merge['Coef'], norm_logp)]
ax.barh(df_merge['Label'], df_merge['Coef'], color=colors_bar, edgecolor='black')
ax.axvline(0, color='black', linewidth=0.8)
ax.set_xlabel("回帰係数", fontsize=12)
ax.set_title(f"{car}:パーツごとの回帰係数(色=有意性)", fontsize=14)
plt.tight_layout()
pdf.savefig(fig, bbox_inches='tight')
plt.close()
7. 散布図・棒グラフ PDF
回帰分析結果を Coef(回帰係数) と -log10(P値) で可視化し、
パーツごとの影響と信頼性を直感的に把握します。
7-1. 散布図(Coef × -log10(P値))の解説
軸の意味
-
X軸(横)= 回帰係数(Coef)
- +側 → 好印象
- −側 → 不評
-
Y軸(縦)= -log10(P値)
- 上に行くほど統計的に信頼できる
- 下のほうは偶然の可能性あり
💡 数値例
- P = 0.05 → -log10(P) ≈ 1.3
- P = 0.01 → -log10(P) = 2
- P = 0.001 → -log10(P) = 3
💡 ポイント
- 右上:好印象かつ信頼性高い
- 左上:不評かつ信頼性高い
- 中央付近:影響小
- 下側:信頼性低
- 点の色:
回帰係数(Coef)の符号で変化- 赤系 → プラス(好印象)
- 青系 → マイナス(不評)
散布図例
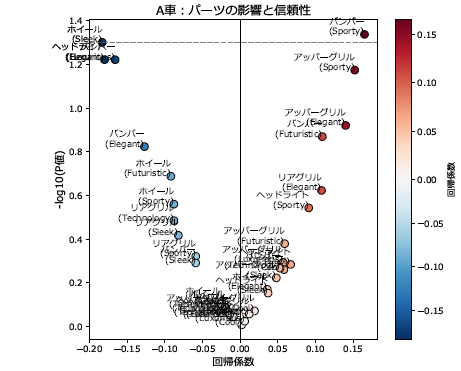
7-2. 棒グラフ(パーツごとの回帰係数)解説
表現の意味
-
横軸= 回帰係数(Coef)
- 棒の長さで影響の大きさを表す
- +なら好印象、−なら不評
-
棒の色の濃さ= -log10(P値)
- 濃いほど信頼性高
- 薄いほど偶然の可能性あり
-
棒の色=
回帰係数(Coef)の符号で変化- 赤系 → プラス(好印象)
- 青系 → マイナス(不評)
💡 数値例
-
P = 0.05 → 色の濃さ ≈ 1.3
-
P = 0.01 → 色の濃さ = 2
-
P = 0.001 → 色の濃さ = 3
-
縦軸ラベル= Trait × Part
- 各性質とパーツの組み合わせを示す
💡 ポイント
- 棒の長さ → 影響の大きさ
- 棒の色の濃さ → 信頼性の高さ
- Trait × Part の比較に便利
い
棒グラフ例
赤=正、青=負、濃い色=有意性が高い
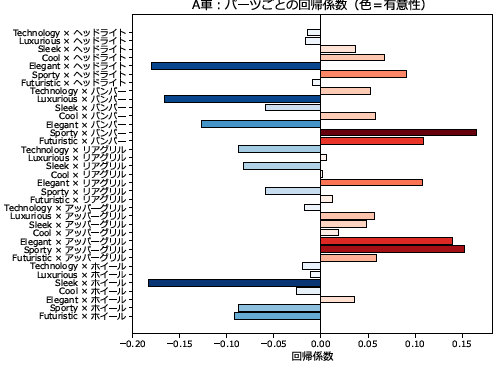
まとめ
-
散布図 = 「鳥の目」
→ 全体像をざっくり俯瞰して、どのパーツが効いているかを直感的に把握できる -
棒グラフ = 「虫の目」
→ 個別パーツをランキング的に比較して、どれが効いているか丁寧に見られる
👉 両方を組み合わせることで、全体感も細部の違いもわかる分析 が可能
# =========================
# レーダー描画関数
# =========================
def plot_radar_ax(ax, df, parts, angles, traits, title, yticks=None):
for part in parts:
vals = df.loc[part].tolist()
vals += vals[:1]
ax.plot(angles, vals, label=part)
if yticks is not None:
ax.set_yticks(yticks)
ax.set_yticklabels([str(v) for v in yticks], fontsize=10)
else:
ax.set_yticklabels([])
ax.set_xticks(angles[:-1])
ax.set_xticklabels(traits, fontsize=10)
ax.yaxis.grid(True, color="gray", linestyle="--", linewidth=0.5)
ax.set_title(title, fontsize=12)
# =========================
# レーダーチャートPDF
# =========================
with PdfPages(save_pdf_re) as pdf:
fig, axes = plt.subplots(2, n_cars, figsize=(6*n_cars, 6*2), subplot_kw={'polar': True}, squeeze=False)
for idx, car in enumerate(cars):
coefs = final_result[final_result['Car']==car].set_index('Trait')[columns_radar].astype(float)
traits = coefs.columns.tolist()
parts = coefs.index.tolist()
angles = np.linspace(0, 2*np.pi, len(traits), endpoint=False).tolist()
angles += angles[:1]
ax = axes[0, idx]
plot_radar_ax(ax, coefs, parts, angles, traits, f"{car}:回帰係数", yticks=[-0.2,-0.1,0,0.1,0.2])
pvals = final_pvalues[final_pvalues['Car']==car].set_index('Trait')[columns_radar].apply(pd.to_numeric, errors='coerce')
log_pvals = -np.log10(pvals.clip(lower=1e-10))
ax = axes[1, idx]
plot_radar_ax(ax, log_pvals, parts, angles, traits, f"{car}:-log10(P値)", yticks=[0,0.5,1,1.5,2])
fig.legend(parts, loc='upper right', bbox_to_anchor=(1.15, 1.0), fontsize=10)
plt.tight_layout()
pdf.savefig(fig, bbox_inches='tight')
plt.close()
8. レーダー描画関数
レーダーチャート描画用の関数を用意し、複数のパーツと Trait に対する回帰結果を可視化できるようにします。
- パーツごとの線を描画し、Trait を軸ラベルとして表示
- Y軸の目盛りやグリッド線で比較しやすく
- チャートタイトルで車種や表示内容(
回帰係数/-log10(P値))を明示
9. レーダーチャートPDF
各車ごとの回帰係数と -log10(P値) をレーダーチャートとして描画。
ポイント
-
上段:
回帰係数(Coef)
→ 各 Trait に対するパーツの影響の方向と大きさ -
下段:
-log10(P値)(logP)
→ その影響の信頼性 - 線の色・スタイル:パーツごとに識別可能
- 軸ラベル(Trait):比較しやすいように統一
- グリッド線・目盛り:視覚的に大きさを把握しやすく
💡 読み方のポイント
- Coef がプラス → 好印象方向
- Coef がマイナス → 不評方向
- logP が大きい → 信頼性が高い
- 線の形・位置でパーツごとの特性を直感的に比較可能
グラフ例
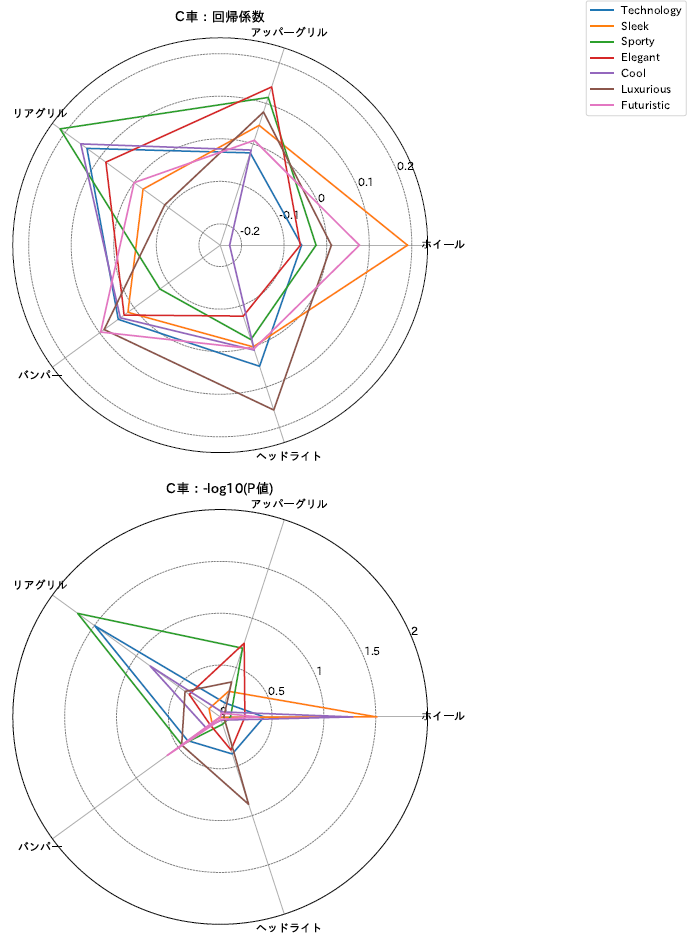
💡 まとめ
- レーダーチャートにより、車ごとのパーツが各 Trait に与える影響を直感的に把握可能
- Coef は「影響の方向と大きさ」、logP は「影響の信頼性」を表す
- 両方セットで読むことが実務上のポイント
📌グラフの使い分けについて
| グラフ | 役割・特徴 | 読みやすさのポイント |
|---|---|---|
| ヒートマップ | 車×Trait のマトリクス形式で影響と信頼性を比較 | Coef と logP をセットで読むと全体傾向と異常値を把握しやすい |
| 散布図(Coef × -log10(P値)) | 全体像を俯瞰して、パーツの影響と信頼性を直感的に把握 | 右上:好印象かつ信頼性高い、左上:不評かつ信頼性高い |
| 棒グラフ(パーツごとのCoef) | 個別パーツの比較やランキングに便利 | 棒の長さ → 影響度の大きさ、色の濃さ → 信頼性 |
| レーダーチャート | 車ごとの全体的なパーツバランスや特徴を俯瞰 | 個別の影響や信頼性の比較には散布図・棒グラフの方が直感的 |
💡 ポイント
- 散布図・棒グラフ → 個別パーツの影響・信頼性を直感的に把握
- レーダーチャート → 車ごとの全体バランスを俯瞰
- ヒートマップ → 車×Trait の全体傾向を一覧比較
- メインは散布図・棒グラフ、補助としてレーダー・ヒートマップを活用すると見やすい
📌考察:回帰係数・-log10(P値) 散布図・棒グラフ
赤=正、青=負、濃い色=有意性が高い

4_5_回帰結果_全車種.csv A車 データ抜粋
| Trait | Part | Coef | -log10(P値) | Label | Car |
|---|---|---|---|---|---|
| Futuristic | ホイール | -0.092 | 0.6882 | Futuristic × ホイール | A車 |
| Sporty | ホイール | -0.088 | 0.5607 | Sporty × ホイール | A車 |
| Elegant | ホイール | 0.036 | 0.1707 | Elegant × ホイール | A車 |
| Cool | ホイール | -0.026 | 0.1046 | Cool × ホイール | A車 |
| Sleek | ホイール | -0.183 | 1.3010 | Sleek × ホイール | A車 |
| Luxurious | ホイール | -0.011 | 0.0453 | Luxurious × ホイール | A車 |
| Technology | ホイール | -0.020 | 0.0894 | Technology × ホイール | A車 |
| Futuristic | アッパーグリル | 0.059 | 0.3799 | Futuristic × アッパーグリル | A車 |
| Sporty | アッパーグリル | 0.152 | 1.1739 | Sporty × アッパーグリル | A車 |
| Elegant | アッパーグリル | 0.140 | 0.9208 | Elegant × アッパーグリル | A車 |
| Cool | アッパーグリル | 0.019 | 0.0721 | Cool × アッパーグリル | A車 |
| Sleek | アッパーグリル | 0.048 | 0.2233 | Sleek × アッパーグリル | A車 |
| Luxurious | アッパーグリル | 0.057 | 0.2941 | Luxurious × アッパーグリル | A車 |
| Technology | アッパーグリル | -0.017 | 0.0721 | Technology × アッパーグリル | A車 |
| Futuristic | リアグリル | 0.012 | 0.0580 | Futuristic × リアグリル | A車 |
| Sporty | リアグリル | -0.059 | 0.3215 | Sporty × リアグリル | A車 |
| Elegant | リアグリル | 0.108 | 0.6234 | Elegant × リアグリル | A車 |
| Cool | リアグリル | 0.002 | 0.0083 | Cool × リアグリル | A車 |
| Sleek | リアグリル | -0.082 | 0.4179 | Sleek × リアグリル | A車 |
| Luxurious | リアグリル | 0.006 | 0.0250 | Luxurious × リアグリル | A車 |
| Technology | リアグリル | -0.088 | 0.4855 | Technology × リアグリル | A車 |
| Futuristic | バンパー | 0.109 | 0.8697 | Futuristic × バンパー | A車 |
| Sporty | バンパー | 0.165 | 1.3372 | Sporty × バンパー | A車 |
| Elegant | バンパー | -0.127 | 0.8239 | Elegant × バンパー | A車 |
| Cool | バンパー | 0.058 | 0.2612 | Cool × バンパー | A車 |
| Sleek | バンパー | -0.059 | 0.2916 | Sleek × バンパー | A車 |
| Luxurious | バンパー | -0.166 | 1.2218 | Luxurious × バンパー | A車 |
| Technology | バンパー | 0.053 | 0.2676 | Technology × バンパー | A車 |
| Futuristic | ヘッドライト | -0.009 | 0.0448 | Futuristic × ヘッドライト | A車 |
| Sporty | ヘッドライト | 0.091 | 0.5436 | Sporty × ヘッドライト | A車 |
| Elegant | ヘッドライト | -0.180 | 1.2218 | Elegant × ヘッドライト | A車 |
| Cool | ヘッドライト | 0.067 | 0.2848 | Cool × ヘッドライト | A車 |
| Sleek | ヘッドライト | 0.037 | 0.1537 | Sleek × ヘッドライト | A車 |
| Luxurious | ヘッドライト | -0.016 | 0.0665 | Luxurious × ヘッドライト | A車 |
| Technology | ヘッドライト | -0.014 | 0.0545 | Technology × ヘッドライト | A車 |
1️⃣ ホイール
-
回帰係数(Coef)- Sleek → 長めの青棒
-
-log10(P値)→ Sleek の棒は濃く、信頼度高め
✅ Sleek : ネガティブ
2️⃣ アッパーグリル
-
回帰係数(Coef)- Sport/Elegant → 赤系棒が長め
-
-log10(P値)→ 棒は中〜濃く、信頼性は中〜やや高め
✅ Elegant/Sporty : ポジティブ
3️⃣ リアグリル
-
回帰係数(Coef)→ 棒は中程度 -
-log10(P値)→ 全体的に淡く、信頼性も低め
✅ 影響ほぼなし
4️⃣ バンパー
-
回帰係数(Coef)- Sporty/Futuristic → 赤系棒が長め
- Luxurious/Elegant → 青系棒が長め
-
-log10(P値)→ 信頼性高め
✅ Sporty/Futuristic : ポジティブ、Luxurious/Elegant : ネガティブ(好みが分かれる)
5️⃣ ヘッドライト
-
回帰係数(Coef)- Elegant → 青系が長め
-
-log10(P値)→ 濃く、信頼性高め
✅ Elegant : ネガティブ
パーツ改善アクションリスト(散布図・棒グラフ版)
| パーツ | 影響方向 | 信頼性(logP) | 推奨アクション |
|---|---|---|---|
| ホイール | ネガティブ(特に Sleek) | 高め | 流麗さやモダンさを損なわないデザインに改善が必要:優先度高 |
| アッパーグリル | ポジティブ(Elegant, Sporty) | 中〜やや高め | 強みとして維持・強化 |
| リアグリル | 影響小 | 低め | 現状維持で問題なし |
| バンパー | ポジティブ(Sporty,Futuristic)、ネガティブ(Luxurious, Elegant) | 高め | Sporty/Futuristic 要素は活かしつつ、Luxurious/Elegant の印象を損なわない調整が必要:優先度高 |
| ヘッドライト | ネガティブ(Elegant) | 高め | 上品さを阻害しないデザイン調整が必要、優先度高 |
💡 改善優先度の見方(散布図・棒グラフ版)
- ネガティブ影響 × 高信頼度 → 優先的に改善
- ポジティブ影響 × 中〜高信頼度 → 強みとして活用
- 影響小 × 信頼性低 → 現状維持
-
回帰係数(Coef)と-log10(P値)はセットで読む
→ 「好/嫌傾向」と「信頼性」を同時に把握可能 - 散布図・棒グラフはパーツごとの影響や信頼性が 直感的に把握できる ため、デザイン改善の優先度を決めるのに便利
- 散布図は点が重なって見えない場合もあるので、2_回帰集計.csv(df_radar)を確認することも有効
考察:回帰係数・-log10(P値)ヒートマップ
散布図+棒グラフと同様の結果になっています。

1️⃣ ホイール
-
回帰係数(Coef)- 青系(負の値)が目立つ
- 特に Sleek は濃い青
-
log10(P値)→ Sleek は濃く、信頼度は高め
✅ Sleek : ネガティブ
2️⃣ アッパーグリル
-
回帰係数(Coef)→ Elegant/Sporty は濃い赤系 -
log10(P値)→ Sporty/Elegant は濃く、信頼性は中〜やや高め
✅ Elegant/Sporty : ポジティブ
3️⃣ リアグリル
-
回帰係数(Coef)→ 全体的に淡い -
log10(P値)→ 全体的に淡く、信頼性は低め
✅ 影響ほぼなし
4️⃣ バンパー
-
回帰係数(Coef)- Sporty/Futuristic → 濃い目の赤系
- Luxurious/Elegant → 濃い目の青系
-
log10(P値)→ Sporty/Futuristic、Luxurious/Elegant は濃く、信頼性は高め
✅ Sporty/Futuristic : ポジティブ、Luxurious/Elegant : ネガティブ(好みが分かれる)
5️⃣ ヘッドライト
-
回帰係数(Coef)- Elegant → 青系
-
log10(P値)→ Elegant は濃い
✅ Elegant : ネガティブ
パーツ改善アクションリスト(ヒートマップ版)
| パーツ | 影響方向 | 信頼性(logP) | 推奨アクション |
|---|---|---|---|
| ホイール | ネガティブ(特に Sleek) | 高め | 流麗さやモダンな印象を損なわないデザインに改善が必要、優先度高 |
| アッパーグリル | ポジティブ(Elegant, Sporty) | 中〜やや高め | 強みとして維持・強化 |
| リアグリル | 影響小 | 低め | 現状維持で問題なし |
| バンパー | ポジティブ(Sporty/Futuristic)、ネガティブ(Luxurious, Elegant) | 高め | Sporty/Futuristic 要素は活かしつつ、Luxurious/Elegant の印象を損なわない調整が必要:優先度高 |
| ヘッドライト | ネガティブ(Elegant) | 高め | 上品さを阻害しないデザイン調整が必要、優先度高 |
💡 改善優先度の見方
- ネガティブ影響 × 高信頼度 → 優先的に改善
- ポジティブ影響 × 中〜高信頼度 → 強みとして活用
- 影響小 × 信頼性低 → 現状維持
-
回帰係数(Coef)とlog10(P値)はセットで読む
→ 「好/嫌傾向」と「信頼性」を同時に把握可能 - 好印象 Trait と嫌悪傾向 Trait を意識することで、デザイン改善の優先度や効果を直感的に理解できる
📌まとめ
-
💡 回帰係数だけで判断はキケンかも
数値が大きいからといって安心せず、log10(P値)も一緒に見ましょう。信頼性の低い結果で判断すると、ちょっと危険です。
-
💡 信頼度を「見える化」
ヒートマップや散布図で、回帰係数(Coef)とlog10(P値)を組み合わせて表示すると、
「どのパーツが本当に影響しているか」がわかりやすくなります。改善優先度を決めるときの参考になります。
-
💡 データの信頼性も大事
- 調査時のイメージワードやパーツの関係を考える
- 分析の閾値やサンプル数が適切かチェック
こういう小さな確認が、結果を安心して使うためのコツです。
-
💡 マーケティング分析は日々進化
新しい手法やツールを取り入れると、
より精度の高い改善ポイントや、優先度の判断がしやすくなります。日々アップデートしていくことが成功の鍵です。
参考リンクについて
GitHubリポジトリ
本記事で紹介したコードやサンプルデータはこちらで公開しています。
Discussion