競技プログラミングをしなくても知っておきたい計算量のはなし
これは ミライトデザイン Advent Calendar 2021 の 14 日の記事です
最近ふぐひれ酒が飲みたくて仕方ない ほげさん ( zenn ) です
今日は計算量について超ゆるふわに紹介してみようと思います
「競技プログラミングとかやらんし」「Web サービス作るのにいらんし」などと思った方!
大量リクエストの対応やバッチ処理など、案外役に立つかもしれないですよ!
どういうときに計算量を考えるか
計算量とは、処理の効率などを示す尺度のことです
この記事では処理時間についてのみ紹介します
まずはサンプルコードと実行結果を見ながら、代表的なケースとインパクトを見てみましょう
- データ構造をちょっとだけ気にする
- ロジックをちょっとだけ気にする
- アルゴリズムをちょっとだけ気にする
の三本立てでサクサクいきますよ
ケース 1: データ構造をちょっとだけ気にする
最後の要素を取得するのは、配列と連結リスト ( 以下、リスト ) どちらが早いか知ってますか?
配列とリストで最後の要素を取得するコードを書いて計測してみましょう
( 調べるのが 1 回だとすぐ終わってしまうので、無駄に 100,000 回繰り返します )
def pattern_array(size: Int): Unit = {
val array: Array[Int] = Array.range(0, size)
val t1 = System.currentTimeMillis()
for (_ <- 0 to 100000)
array(size - 1) // ← 注目
val t2 = System.currentTimeMillis()
println(s"% 6d ms".format(t2 - t1))
}
def pattern_list(size: Int): Unit = {
val list: List[Int] = List.range(0, size)
val t1 = System.currentTimeMillis()
for (_ <- 0 to 100000)
list(size - 1) // ← 注目
val t2 = System.currentTimeMillis()
println(s"% 6d ms".format(t2 - t1))
}
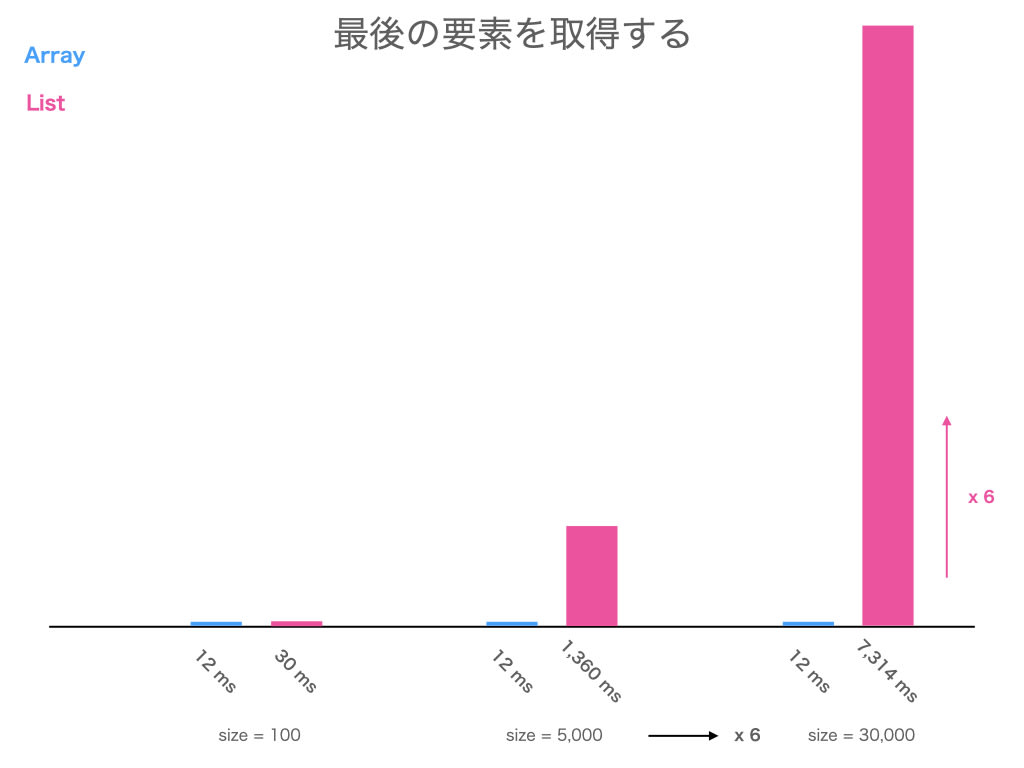
size が 100, 5,000, 30,000 で計測しました
呼び出し部のコード
pattern_array(100)
pattern_list(100)
pattern_array(5000)
pattern_list(5000)
pattern_array(30000)
pattern_list(30000)
どちらが どれくらい 遅いのか、予想して結果を開いてみてください
結果
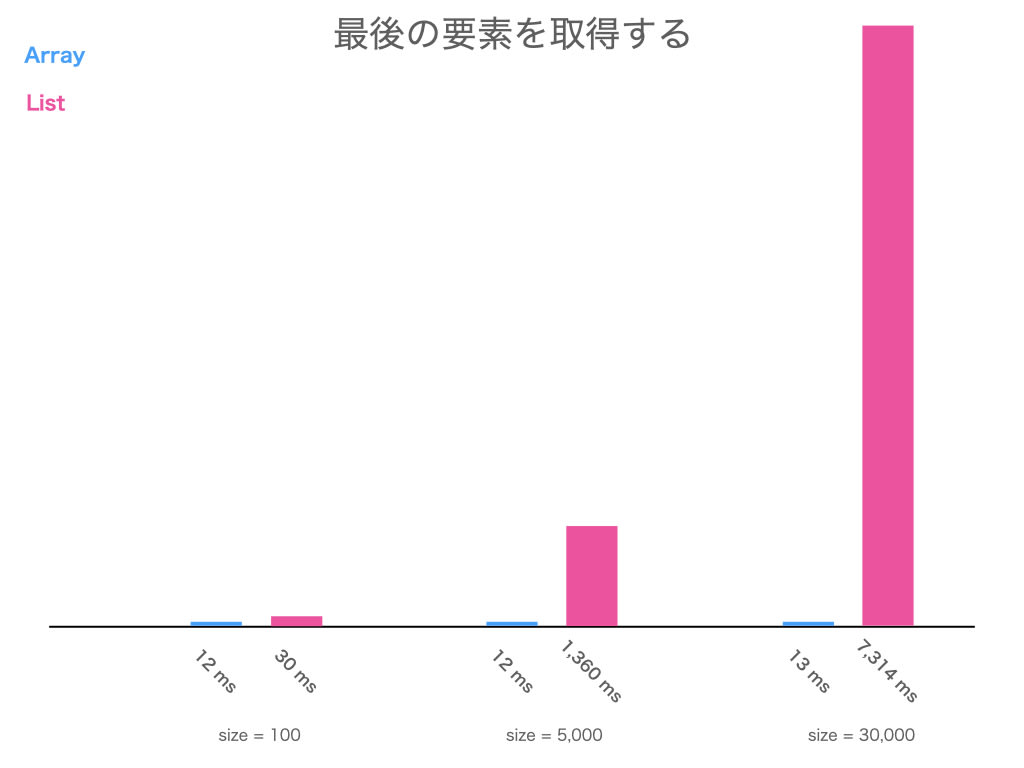
と言うことで、配列よりリストの方が遅い のでした!
なんで?
配列とリストのデータ構造を見てみましょう
配列はメモリを連続して確保してそこに順に値を入れます
変数 array は配列の先頭の番地 ( A3 ) を表しているポインタにすぎません
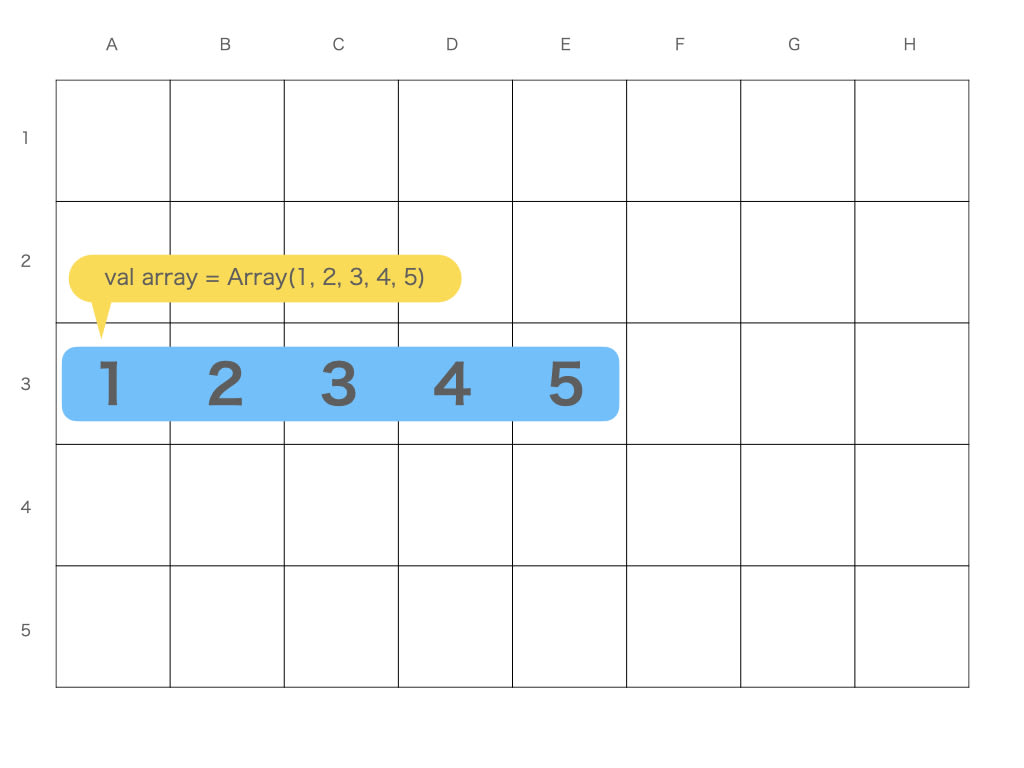
対して、リストはメモリを連続して確保せず、次の場所を知ることで繋がっています
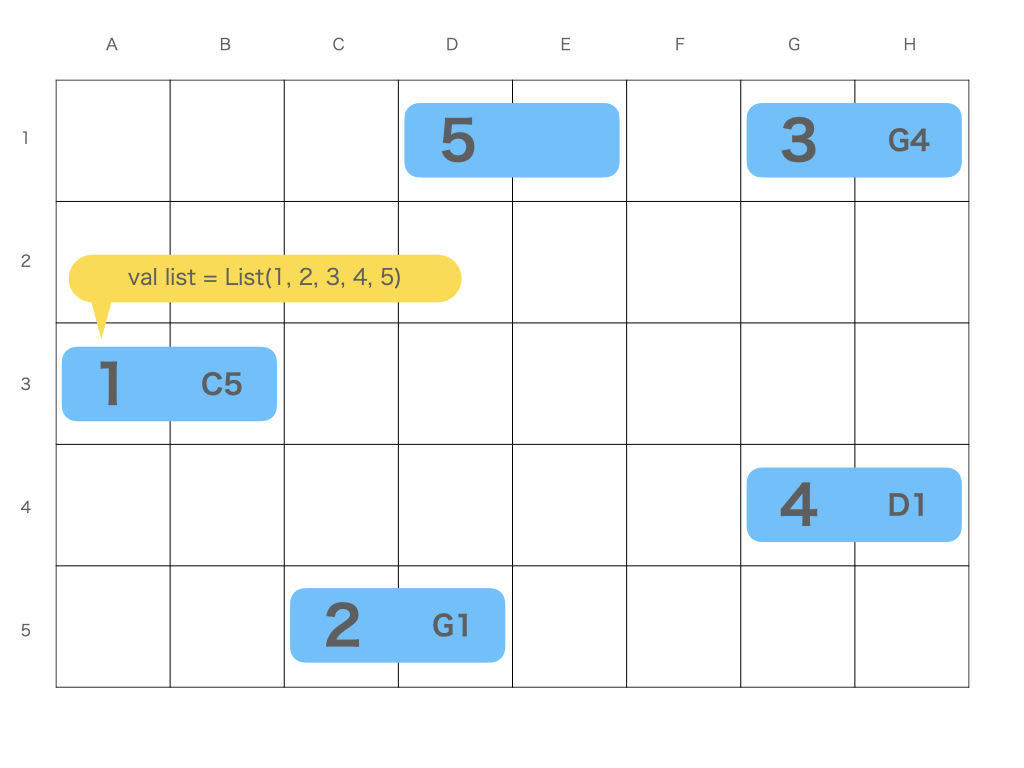
これを踏まえ、変数から 5 番目の要素 ( 5 ) を取り出す手間を 手数で数えてみましょう
まず配列です
変数 array でまず最初に見る場所は A3 とわかります
そして 連続して確保しているので 5 番目の場所は 4 つ右 だとすぐわかります
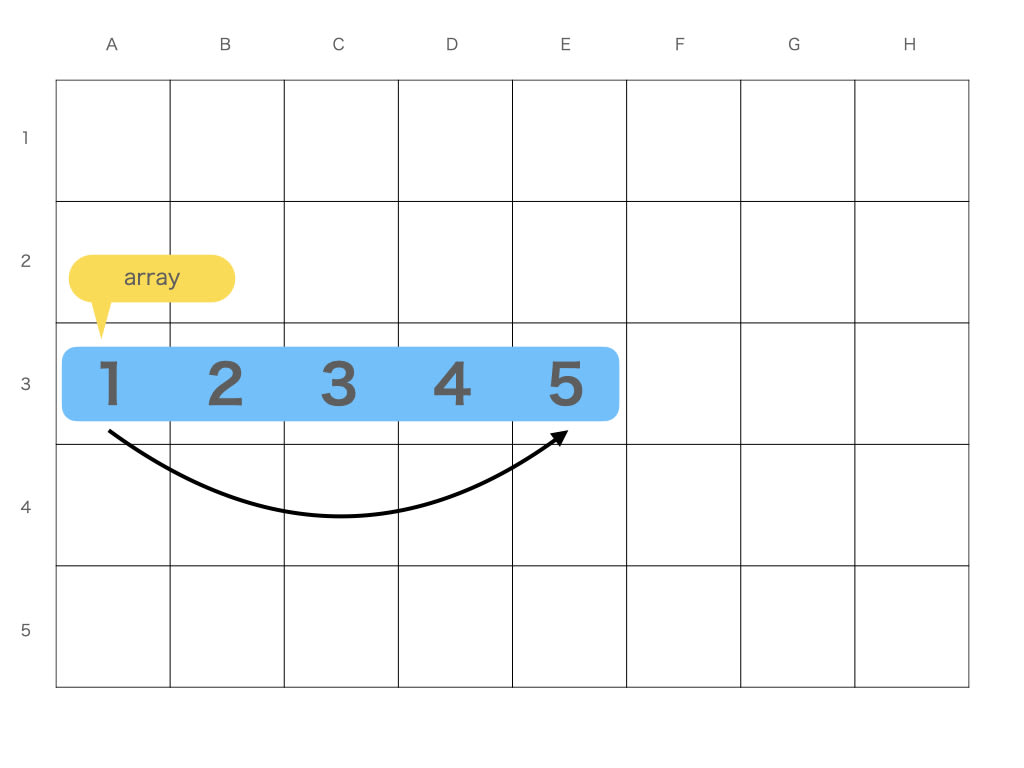
矢印の数を数えてこれを 1 手 と呼ぶことにします
対して、リストは 辿らないと最後の要素がどこなのかわかりません
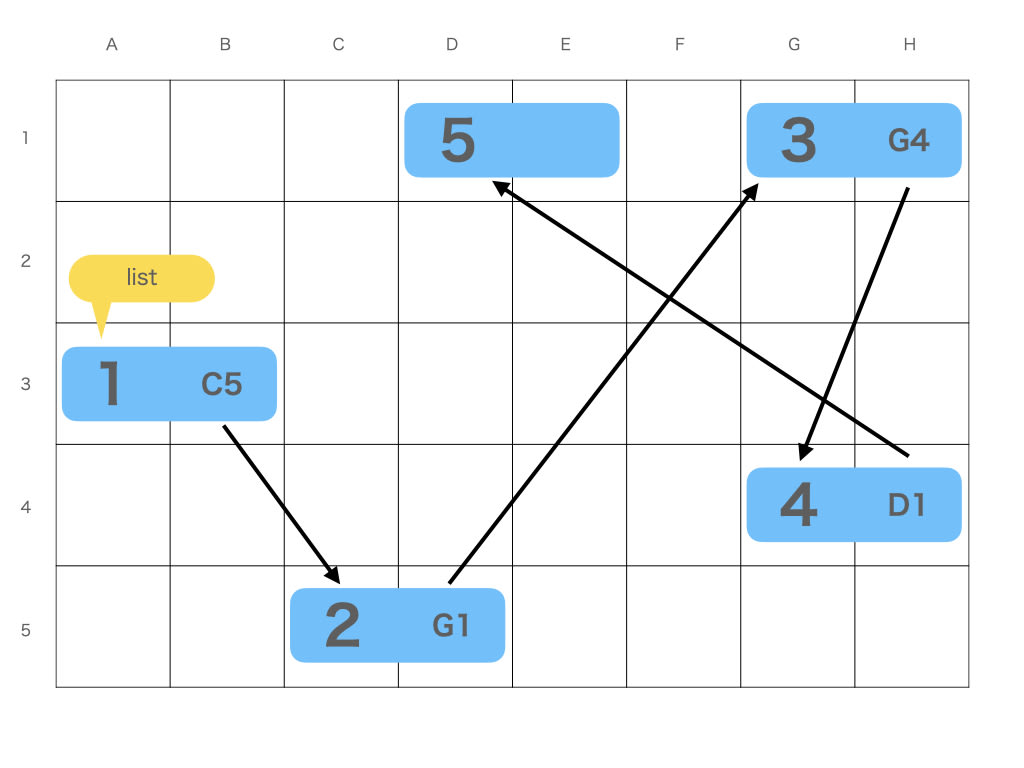
同じく矢印の数から、これを 4 手 と呼ぶことにします
この手数の違いが性能の違いになります
処理回数の目安を表現する
ある操作をするときの手数を 計算量 と言い、Order の O を使い O(n) などと言ったりします
まずリストですが、リストの最後の要素の取得は O(n) と表現します
n はリストの大きさのことです
O(n) はリストの長さと手数が比例する ことを教えてくれています
例えば「長さ 100 のリストの最後の要素の取得は 100 手」ということを表しています
対して 配列の最後の要素の取得は O(1) です
n が出てきていないので、リストの大きさに左右されません
つまり O(1) は配列がどんなに大きくなっても性能が劣化しません
「長さ 100 の配列の最後の要素の取得は 1 手」ということです
よりみち: じゃあリストって使わないほうがいいの?
そんなことはありません
たとえば配列は先頭に要素を増やすのは遅いです
より大きなメモリを確保して、中身を移し替えてから、作った隙間に値を入れます
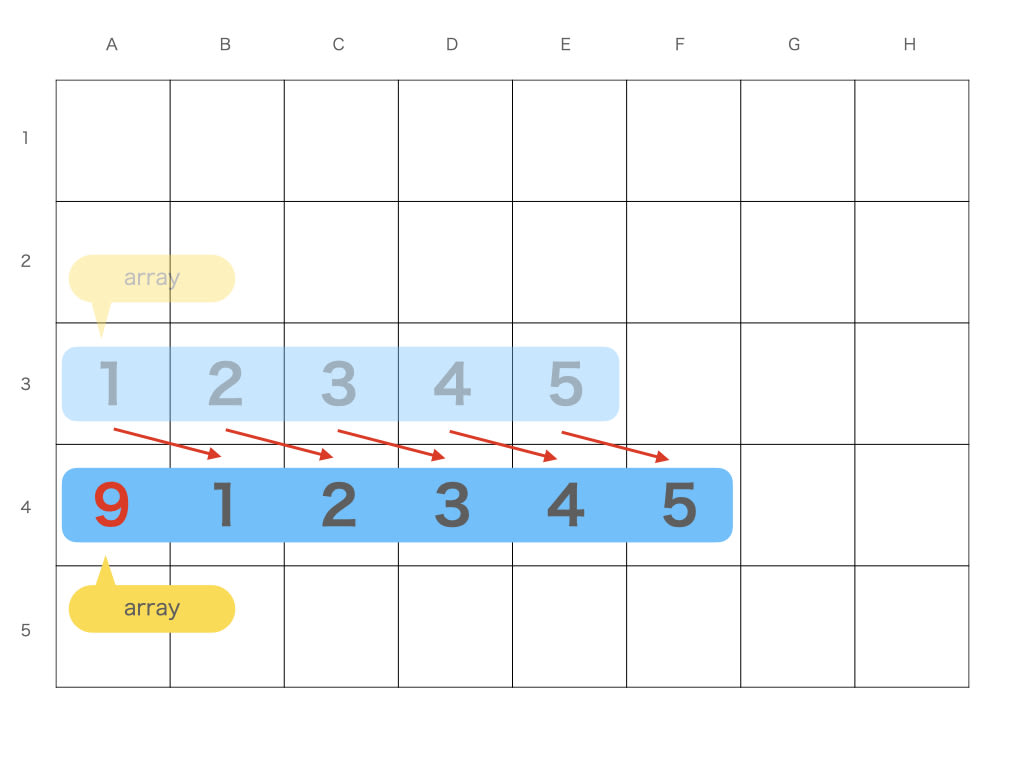
対して、リストは先頭の前にひとつ要素を増やして矢印を 1 本ひくだけなので速いです
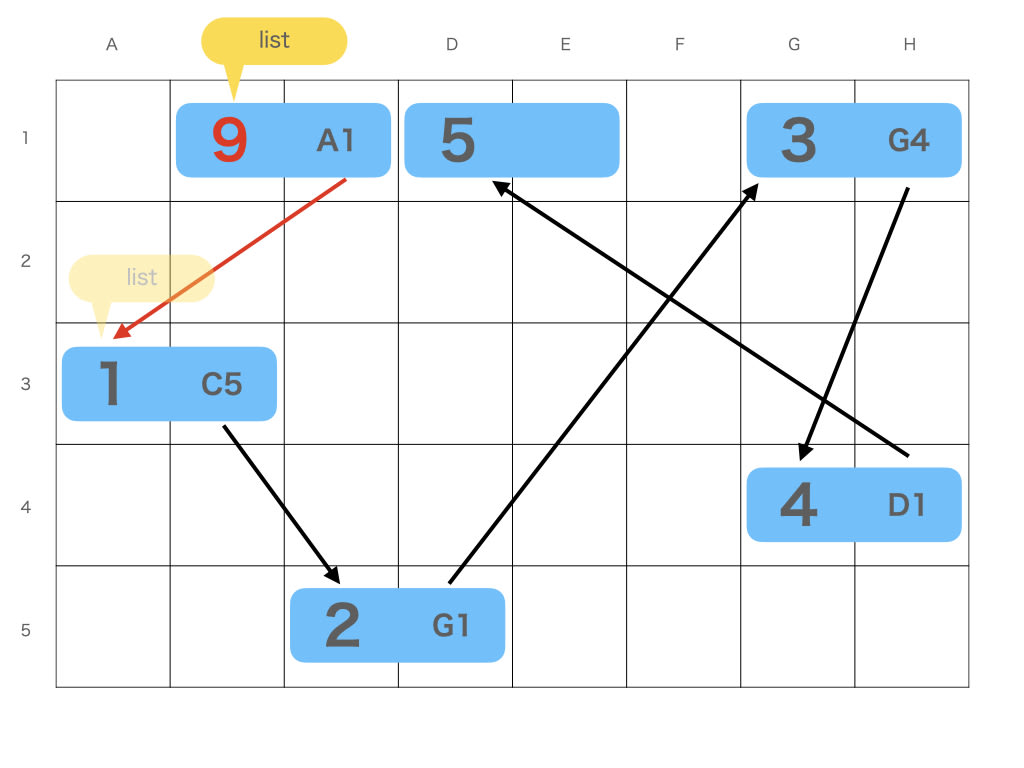
行う処理に応じて適切なデータ構造を選ぶことが大切です
まとめ
大きさに連動しない配列 vs 大きさに連動するリスト
という違いでした
- 処理とデータ構造によって 手数 が全然違い、計算量 というので表現する
-
計算量 は
O(n)とかO(1)と書き、大きさに比例するかなどをアピールできる - 処理に適切なデータ構造を選ぶのが大切
ケース 2: ロジックをちょっとだけ気にする
データ構造ではなくどんなコードを書いたかも重要です
たとえば利用明細みたいな配列があり、それぞれの明細が総額の何割を占めるか出力します
総額 ( total ) を作るタイミングを 1 行だけ変えた 2 つのコードの性能を比べてみましょう[1]
def pattern_outside(size: Int): Unit = {
val array: Array[Int] = Array(0, size)
val t1 = System.currentTimeMillis()
val total = sum(array).toDouble // ← 注目
for (i <- array.indices) {
println(i / total * 100 + "%")
}
val t2 = System.currentTimeMillis()
println(s"% 6d ms".format(t2 - t1))
}
def pattern_inside(size: Int): Unit = {
val array: Array[Int] = Array(0, size)
val t1 = System.currentTimeMillis()
for (i <- array.indices) {
val total = sum(array).toDouble // ← 注目
println(i / total * 100 + "%")
}
val t2 = System.currentTimeMillis()
println(s"% 6d ms".format(t2 - t1))
}
size が 5,000, 10,000, 50,000 で計測しました
呼び出し部と sum のコード
pattern_outside(5000)
pattern_inside(5000)
pattern_outside(10000)
pattern_inside(10000)
pattern_outside(50000)
pattern_inside(50000)
def sum(array: Array[Int]): Int = {
var res = 0
for (i <- array.indices) {
res += array(i)
}
res
}
どちらが どれくらい 遅いのか、予想して結果を開いてみてください
結果
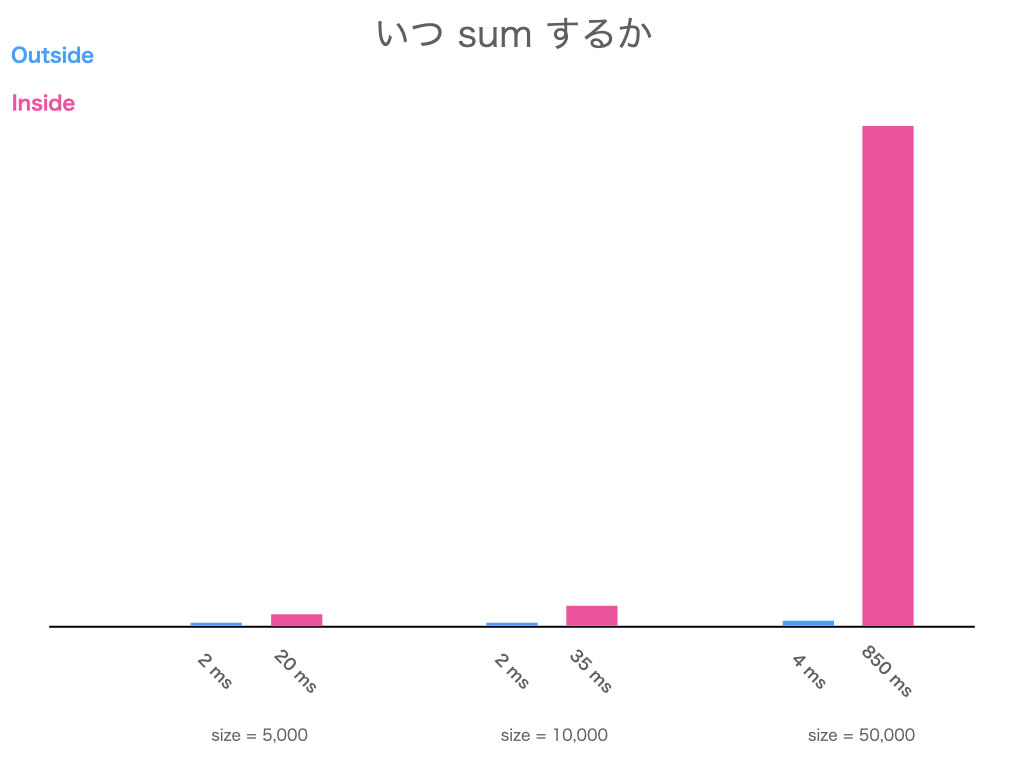
と言うことで、ループの内側で sum する方が圧倒的に遅い のでした!
なんで?
二重ループになっているからです
for の手数は要素数に比例するので O(n) です
また、sum も全ての要素を確認しないと総和が作れないので O(n) です[2]
size = 5 だとして、sum を for の外でした場合は sum 1 回と for 1 周なので 5 + 5 手 です
2n ですね
対して sum を for の中でした場合は sum を 5 回実行するので 5 * 5 手 です
こちらは n^2 ですね

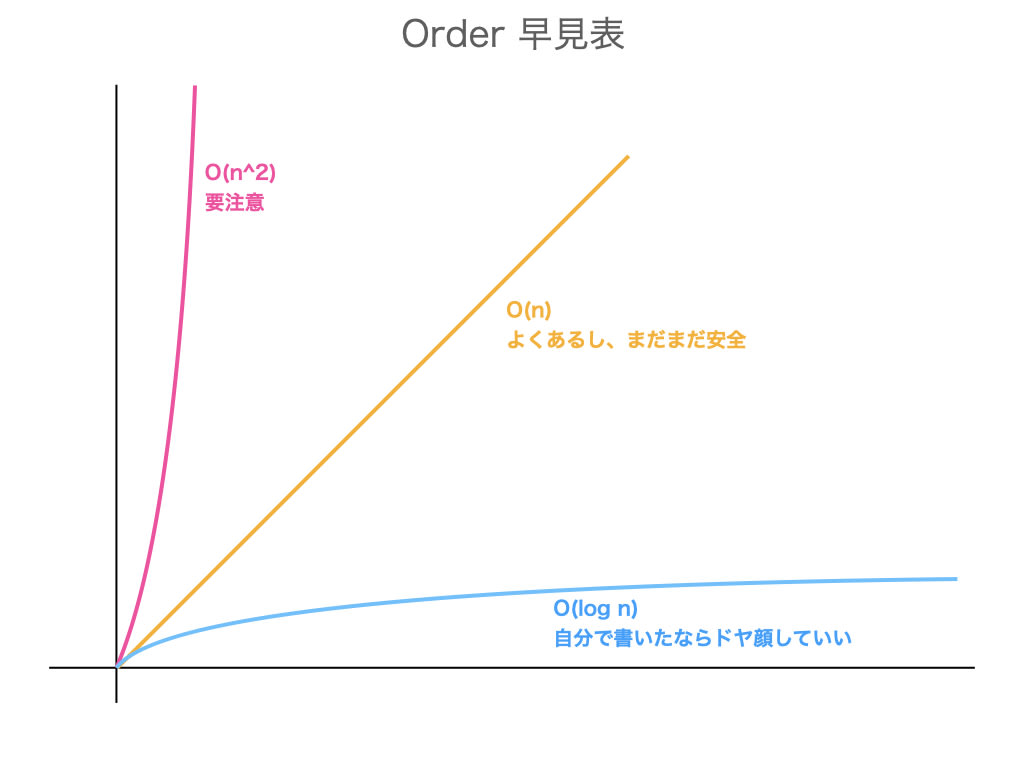
二重ループは要注意
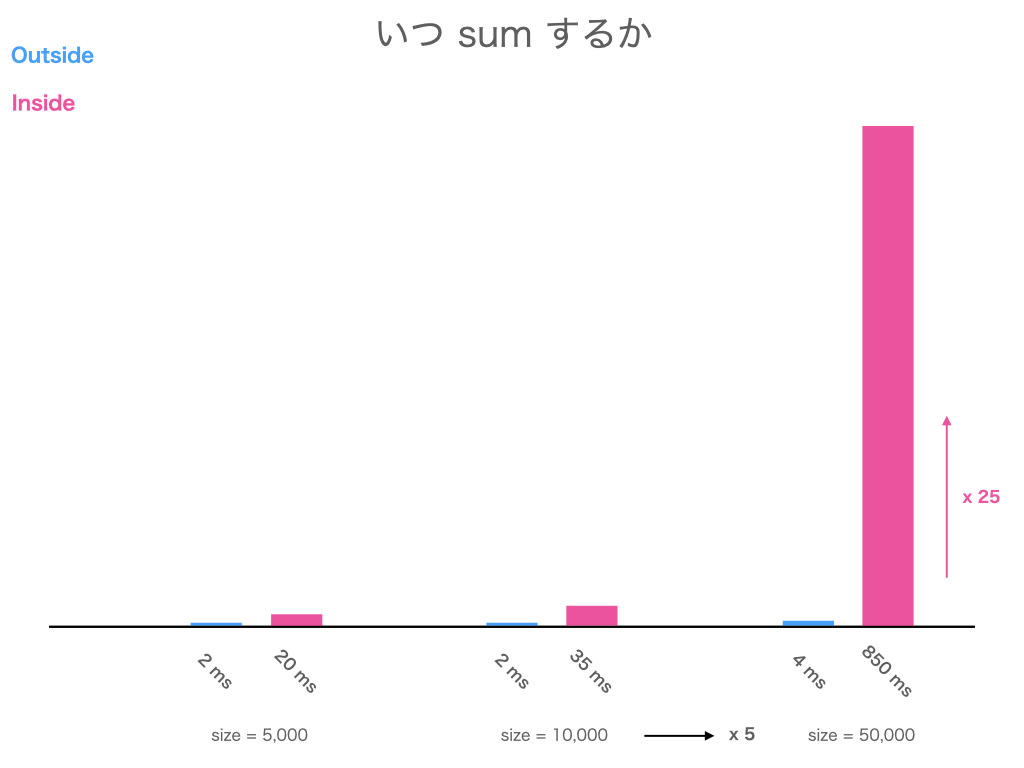
O(n^2) は 要素数の二乗に比例します
size = 10,000 で 1 億手、size = 50,000 で 25 億手 です
要素数が大きくなる場合は、可能な限り O(n^2) は避けられると良いでしょう
よりみち: 係数はあんまり気にしなくて大丈夫
係数とは 2n の 2 の部分です
size = 50,000 の 2n は 10 万手ですが、n^2 の 25 億からしたら 5 万は誤差 ですね
大雑把に考えれば 二乗が出てこなければおk という感じなので、この記法では 2n の 2 は略して O(n) と書きます
O(n) だぜ ( → 比例くらいは問題ないぜ )
O(n^2) だぜ ( → おいおいちょっとどうにかならんのか )
なんて会話をするには係数がなくても十分ですね
まとめ
大きさに連動する実装 vs 大きさの二乗に連動する実装
という違いでした
-
O(n)ループ とO(n)処理を呼ぶなら2nで、O(n)と書いてしまう -
O(n)ループ の中でO(n)処理を呼ぶとO(n^2)と書く -
O(n^2)は要注意 - 直接
forがふたつ見えなくても、油断してはならない
ケース 3: アルゴリズムをちょっとだけ気にする
自分で書いたコードに限らず、使っているコードがどんなロジックになっているかも重要です
巨大な配列の中にある値が含まれているか、contains と search で調べてみましょう
( 調べるのが 1 回だとすぐ終わってしまうので、無駄に 10,000 回繰り返します )
def pattern_search(size: Int): Unit = {
val array: Array[Int] = Array.range(0, size)
var b = false
val t1 = System.currentTimeMillis()
for (_ <- 0 to 10000)
if (array.search(size).isInstanceOf[Found]) // ← 注目
b = true
val t2 = System.currentTimeMillis()
println(s"% 6d ms".format(t2 - t1))
}
def pattern_contains(size: Int): Unit = {
val array: Array[Int] = Array.range(0, size)
var b = false
val t1 = System.currentTimeMillis()
for (_ <- 0 to 10000)
if (array.contains(size)) // ← 注目
b = true
val t2 = System.currentTimeMillis()
println(s"% 6d ms".format(t2 - t1))
}
size が 1,000, 10,000, 80,000 で計測しました
呼び出し部のコード
pattern_search(1000)
pattern_contains(1000)
pattern_search(10000)
pattern_contains(10000)
pattern_search(80000)
pattern_contains(80000)
どちらが どれくらい 遅いのか、予想して結果を開いてみてください
結果
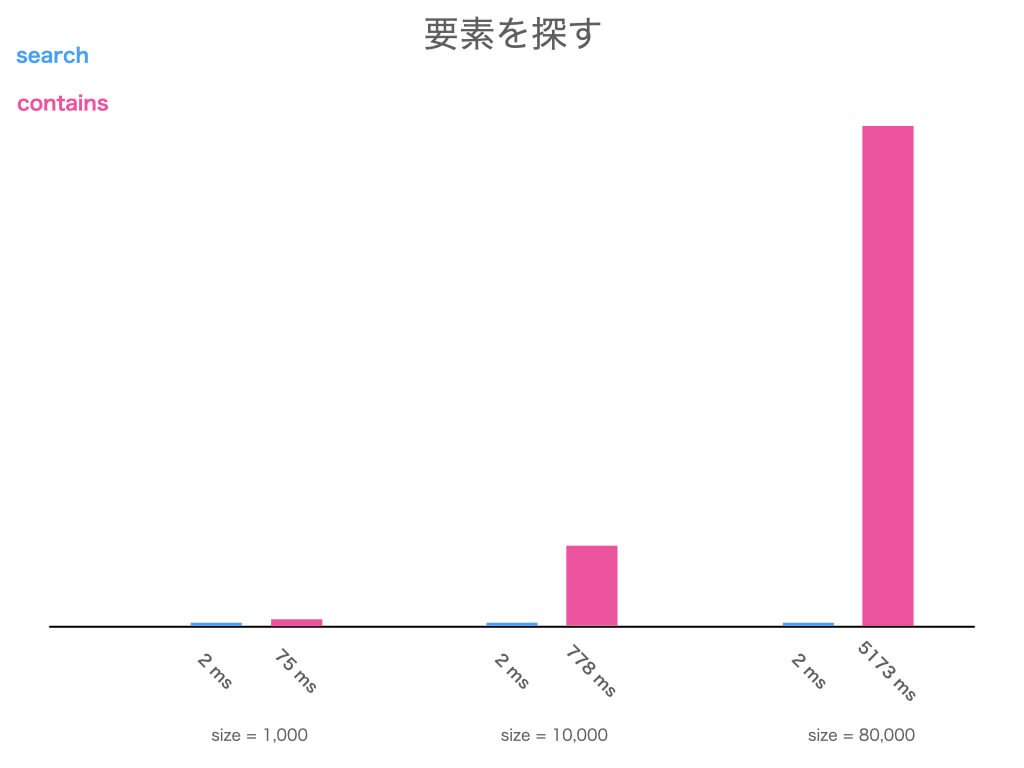
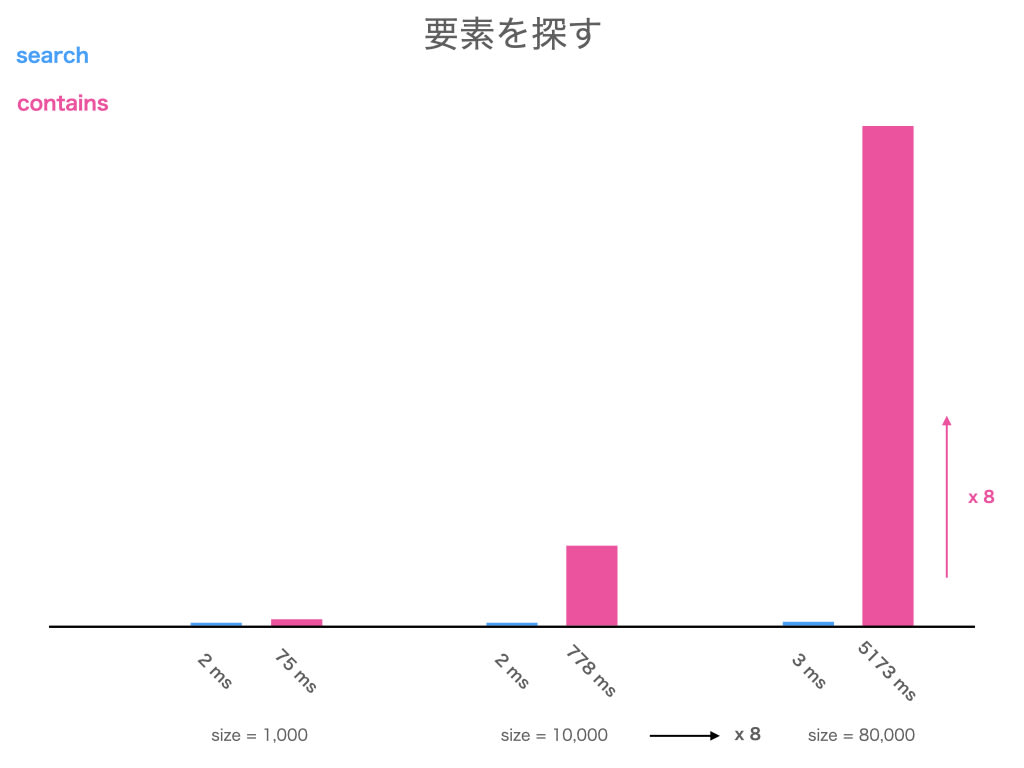
と言うことで、contains は search より遅い のでした!
なんで?
contains は配列から 見つかるまで先頭から順に調べます
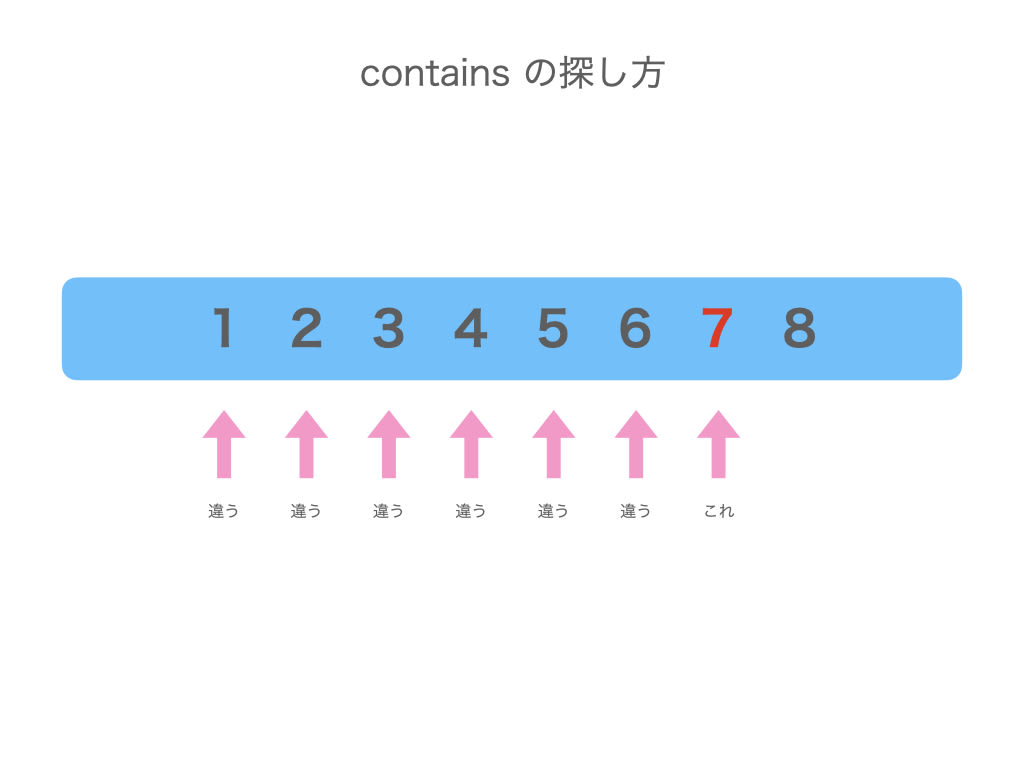
search は配列を 半分に半分にしながら調べます
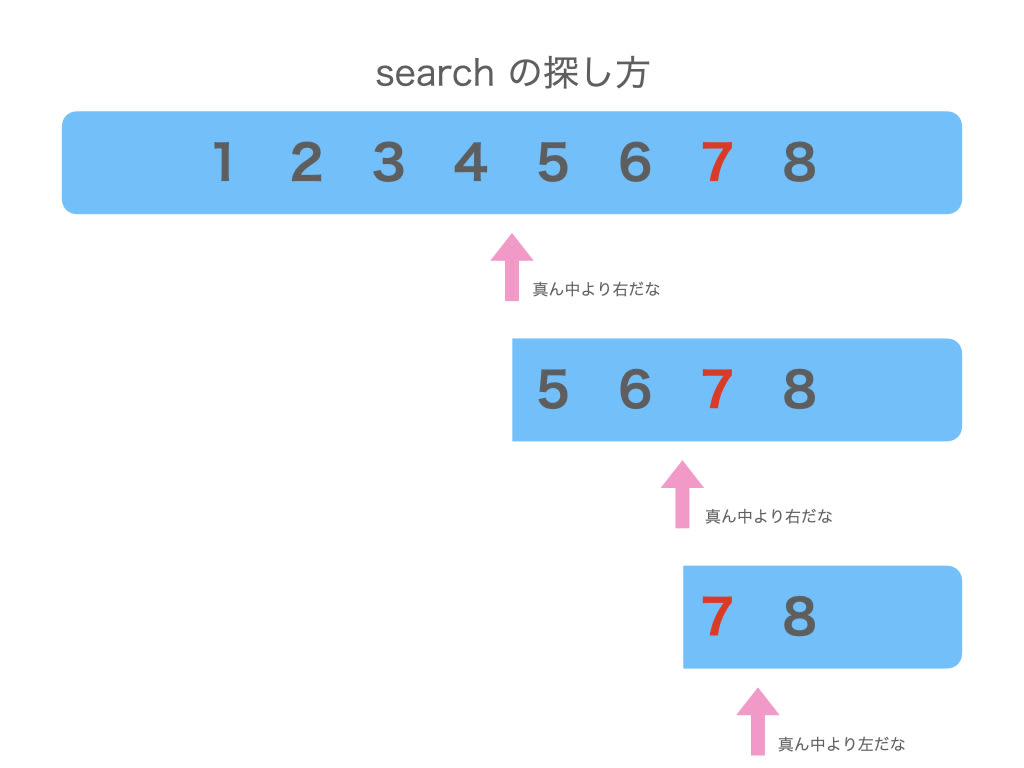
search の方が速いのは半分ずつ調べる範囲を削るからですが、contains と違い「大小比較ができること」や「ソートされていること」という制約もあります
状況に応じて使い分けることが大切です
比例より速い世界へ
contains は要素の数に比例するので O(n) です
対して search は n が 2 倍になるとやっと 1 手 増えます
これを O(log n) と言います
O(log n) は超速いです
10,000 を 13 回半分にすると 1 になります、つまりたったの 13 手 で調べ切れます
要素が 10,000 から 80,000 に増えても、倍の倍の倍なので 手数が 3 しか増えません
O(log n) が O(n) に対して圧倒的に速いのがわかりますね
ちなみに、search のアルゴリズムは二分探索 ( binary search ) と言います
DB の Index なんかも近しいアルゴリズムが使われています[3]
よりみち: log のイメージがわかない
砕いて言えば 2 の何乗なのさ ということです
Python などで 2 ** 10 とかしてでた値が 10 手 で調べ切れる大きさです
python> 2 ** 10
1024
python> 2 ** 20
1048576
python> 2 ** 30
1073741824
すさまじいですね
まとめ
大きさにほぼ連動しない search vs 大きさに連動する contains
という違いでした
-
O(log n)は超速い - 自分で
O(n)より速くするのはかなり工夫が必要 - 書けなくても全然良いけど、ソートや DB の Index などを考えるときに知っていると良い
いつものプログラミングに活かすには
ここまで 3 ケース紹介しました
「え、そんなに違うの??」と驚いたのではないでしょうか
難しそう...
ゴリゴリいろんなアルゴリズムを書けない...
ガリガリのチューニングを求められていない...
と、しても!
やれることはいっぱいあります!
兎にも角にも二乗を避ける
ケース 2 で見たとおり、O(n^2) が登場してしまったときのインパクトが一番大きいです
どうしても避けられないことはありますが、普段から二重ループに気を付けると良いでしょう
for がなくても、1 行でも、こういうのも二重ループですよ
users.filter(user -> user.id in someList)
n がどれくらいか考える
「someList は 30 までだし、うちのサービスは users も 1 万だから、高々 30 万だよ」
という上限が見えていれば安心できます
逆に「someList は 1 万、users は 100 万」ということがわかっていれば、本番環境にリリースする前に実装を見直すことができるかもしれません
n の増え方と処理時間への影響を考える
1 万の someList が毎月 1 万増えるとしたら、これはかなり危険です
1 年で 10 倍くらいの時間がかかるようになってしまうかもしれません
in の実装を見直す ( O(n) から O(log n) に変える ) とか
filter 処理を DB で済ませる ( インデックスに頼る ) といった
修正が必要になるかもしれません
処理時間が妥当か考える
競技プログラミングでは ただのループだと 1 秒で 1 億週くらい が目安とされているみたいです[4]
オンライン処理で計算量が 1 億になるようなことはまずないし、複雑な計算や DB アクセスなどが伴うので実際はもっと遅くなりますが、目安として覚えておく価値はあるでしょう
「二重ループがあるから計算してみたら 30 万だったよ、で、30 万ってやべぇの?」
→ 「それくらい大したことないよ」
「20 万の csv を 1 行ずつ読み込んで保存するバッチを作ったら 3 時間かかったよ」
→ 「なんか妙に遅くない?」
というくらいの感覚は身につけることができるようになるはずです
普段使っている処理の計算量を想像する
xxx 法や yyy 法を覚えるのも良いことですが、その前にもっと普段からできることがあります
「この処理って O(n) かな?」
「あれ、この実装って実質二重ループ ( O(n^2) ) になってね?」
「標準ライブラリ使ったらオレオレ実装より速い ( O(log n) ) かも?」
と普段の実装のときから意識することです
「sum は全部の要素を足すのだからきっと O(n) だろう」
「map, filter, reduce なんかも全要素に対して処理をするのだから O(n) だろう」
→「じゃあ users.filter(user -> user.score > points.sum) はマズイのでは...」
「contains って O(n) かな? もっと速いのかな?」
→「調べてみたら O(n) だ、ちょっと困るな」
「sort ってこんなバシバシ叩いても性能的に大丈夫なのかな?」
→「調べてみたら O(log n) だ、全然おk」
「この for の中に list.append あるけど、for って何周くらいするんだっけ?」
→「n = 100 くらいなら全然いっか」
→「n = 10 万 はヤバい、list.prepend + list.revert にしなきゃ」
など、ちょっと考えてみるだけで見えてくることはいろいろあります
おわり
僕も全然競技プログラミングガチ勢ではないですが、普段から O(n), O(n^2), O(log n) を 1 年くらい意識してたら、だいぶ自然と意識できるようになりました
最近では不必要な O(n^2) にすぐ気付いて O(n) x O(log n) に修正し、数時間の時間短縮に繋がったこともあります
この記事で少しでもそういうことに興味を持ってもらえたら嬉しいです
計算量について学んで整理しているらしいので、どんな内容か楽しみです
おまけ: 実例っぽいもの
やること
- csv で利用明細が来る
- DB にいる user だれかの明細なので探して、明細を紐づける
- 処理対象者リストを書き出す
Before
var result: List[Int] = List.empty
for (line <- csv) { // csv で利用明細が来る
val (userId, price) = parse(line)
val user = findById(userId) // DB にいる user だれかの明細なので探して
writePayment(user, price) // 明細を紐づける
}
for (line <- csv) {
val (userId, _) = parse(line)
result :+= userId
}
successLog(result) // 処理対象者リストを書き出す
After
var result: List[Int] = List.empty
for (line <- csv) {
val (userId, price) = parse(line)
val user = findById(userId) // アルゴリズムを気にしてインデックスを貼った
writePayment(user, price)
// ロジックを気にして for を統合した
result +:= userId // データ構造を気にして先頭追加にした
}
successLog(result.reverse)
結果
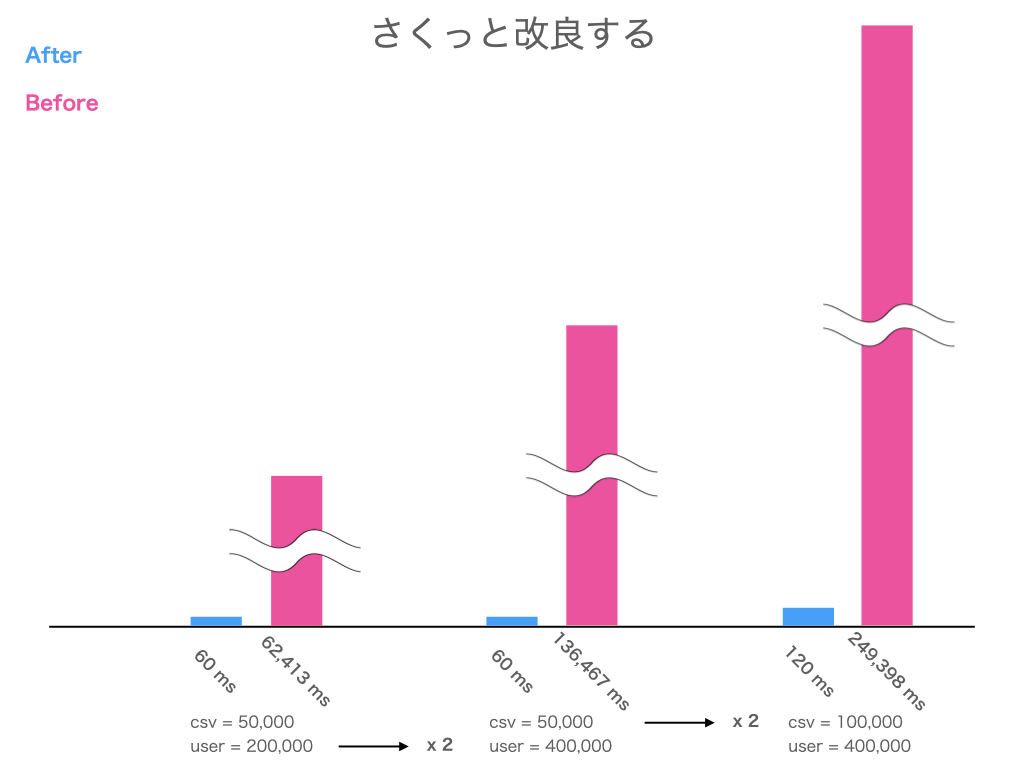
csv の行数にだけほぼ連動する高速化ができました
Discussion