Transformerを理解したい

Transformerを理解したい記事です。

Transformerが提案された論文「Attention is All you need」をベースにまとめていきます。

以下の知識があることを前提としています。

• Deep Learningに関する基礎的な知識
• RNNに関する基礎的な知識
• 上記に関連する数学的知識

大雑把に言えば、Deepは使っているけどTransformer関連だけは経験がないような人向けになります。

Transformer誕生の背景

Transformerは、自然言語処理など系列モデリングの文脈で登場したモデルです。

入力系列を別の系列に変換するタスクはSeq2Seqと呼ばれ、入力を隠れ状態にエンコードするEncoderと、出力系列へ変換するDecorderからなるため、Encoder-Decoderモデルとも呼ばれます。

Transformer登場以前のDeep LearningによるEncoder-DecoderモデルにはRNNベースのモデルが使われていました。しかし、RNNベースのEncoder-Decoderモデルには以下の問題がありました。

1. Encoderの出力が固定長ベクトルになる。
2. Decoderへの入力が、Encoderから出力された最後の隠れ層のみ。

これらの問題を解決したのがTransfomerです。そして、その本質は、Transformerブロック内部にあるAttention機構にあります。以下でまとめていきます。

Transformerの構成要素

Transformerは以下のような構造をしています。

[1] Figure 1 より引用

Nxは、このブロックがN回繰り返されるという意味です。

Transformerを理解するには、この図にあるブロック

1. Multi-Head Attention
2. Positional Encoding
3. Feed Forward
4. Add & Norm

を理解する必要があります。また、Multi-Head Attentionを理解するためには、Attentionを理解しておく必要があります。

Attention

Multi-Head Attentionの前に、Attentionについて知っておきましょう。Attentionとその派生形であるMulti-Head Attentionは以下のような構造をしています。

[1] Figure 2 より引用

計算内容はともかく、Multi-Head Attentionは複数個のAttentionの計算結果を結合したものになっているのがわかると思います。

Attentionの概念

Attentionは入力のどの部分に注目するべきか選択する機構で、以下の式で与えられます。

$$\begin{align} \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \end{align}$$

$Q, K, V$ はそれぞれクエリ、キー、バリューと呼ばれる行列です。

一旦数学のことは忘れて用語だけ説明すると、クエリは検索キーワード、キーとバリューは辞書に対応します。つまり、入力された検索キーワードにもっとも近しいキーを選び、対応するバリューを得るということを上記の式は表しています。

• 近しいキーを選ぶ　→　$Q$と$K$の内積を取ってsoftmax
• 対応するバリューを得る　→　softmaxの結果と$V$の内積を取る

ということです。キーを選ぶといっても本当に1つの要素だけを選ぶと微分不可能になる不都合があるので、softmaxで代用しています。softmax後に最も値が大きい要素を選ぶと、我々が辞書を引くのと同じような「キーを選ぶ」という操作になります。「$K, V$ はどう決めるんだ」、「$\sqrt{d_k}$ ってなんだ」という声が聞こえてきそうですが、この後説明します。

Scaled Dot-Product Attention

さて、式 (1) はScaled Dot-Product Attentionというのが正式名称で、一般的にAttentionと呼ばれるものは大体これです。

Dot-Productというのが 式 (1) における $QK^T$ のことで、Scaled というのが $\sqrt{d_k}$ のことですね。ここで、$\sqrt{d_k}$ はキー $K$ の次元を表します。なぜこんな計算をするのか理解するために式 (1) を視覚的に確認しましょう。

まず、 $QK^T$ の Dot-Product（内積）では以下の計算を行っています。簡単のためにひとつのクエリで考えます。

$QK^T$ の新しく Attention weight というものが登場していますが、要はクエリとキーの類似度を表しています。与えられたクエリに対して類似度を計算し、softmaxを取ることでクエリに対するキーの重みを得ます。そして、得られたAttention weightでバリューの加重平均を取ります。

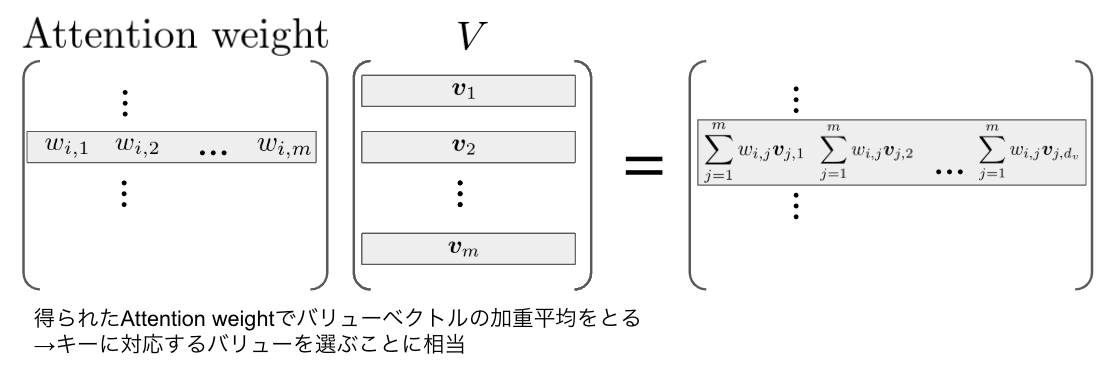
簡単のため、Attention weightの要素を $w_{i,j} = \boldsymbol{q}_i \cdot \boldsymbol{k}^T_j$ と置きました。Attention weightのいずれかの要素が $1$ それ以外は $0$ の場合、クエリで検索したキーに対応するバリューを選んでいることになります。

"Scaled"の謎

$n$ 次元単位超球を考えましょう。ナニソレという方は、円と球をイメージしたら良いです。半径はいくつになるでしょうか。単位円の半径は $\sqrt{1^2 + 1^2} = \sqrt{2}$ 、単位球の半径は $\sqrt{1^2 + 1^2 + 1^2} = \sqrt{3}$ になりますね。$n$ 次元だと $\sqrt{1^2 + 1^2 + \ldots + 1^2} = \sqrt{n}$ になります。つまり、次元が大きくなるとこの半径はどんどん大きくなってしまいます。

ここで、 $QK^T$ の計算を振り返ってみると、Attention weightの次元はキーの次元で決まっていることがわかると思います。我々がこの計算で知りたいのは、クエリとキーの類似度です。次元の大きさによって計算結果が変化してしまうと困るので、$\sqrt{d_k}$ でスケーリングするわけですね。

Multi-Head Attention

さて、ここまでAttentionことScaled Dot-Product Attentionの説明をしてきました。複雑に見えて原理は単純な事がわかったかと思います。そしてここまで学習可能なパラメータが一切出てきていないことに気が付いたでしょうか？つまり、単純な内積と加重平均のみでAttention機構は実現されています（すごい）。ただ、このままでは当然モデルの学習はできません。Attentionを学習可能な形にしたものがMulti-Head Attentionというわけです。

ここで、Multi-Head Attentionの図を見直してみましょう。Attention layerの入力前にLinear layerによる線形変換が行われていることがわかります。この部分がAttention機構の学習を担ってくれています。そして、$h$ 個のAttention（それぞれをheadと呼ぶ）の結果を結合するのでMulti-Head Attentionと呼びます。式で書くと以下のようになります。

$$\begin{aligned} \text{MultiHead}(Q, K, V) &= \text{Concat} (\text{head}_1, \ldots, \text{head}_h) W^O \\ \text{where head}_i &= \text{Attention} \left(QW_i^Q, KQ_i^K, VW_i^V \right) \end{aligned}$$

ここで、$W_i^{\left\{Q,K,V\right\}}$ が図のLinear layerに対応します。Concatでheadを1行に結合して、$W_O$ でheadの加重平均を取っています。Concatするところで出力の次元がheadの数だけ増えてしまいそうですが、Linear layerのところで次元を $1 / h$ に落としています。

なぜMulti-Headにしたかなのですが、その方が性能が良かったからと著者らは言っています。異なる位置の異なる部分空間表現を学習できるからとのことです（特にこれ以上のことは書かれていませんでした）。

K、Vの決め方

今まで $Q, K, V$ は暗黙的に与えられるものとして来ましたが、実は基本的に $Q=K=V$ です。つまり、$Q, K, V$は入力それ自身なのでした。このような場合のAttentionを特にSelf-Attentionと呼びます。$Q$ はクエリなので、入力であることに違和感はありませんが $K, V$ も同じってどういう事なのでしょうか。

$Q=K=V$ の状況で式 (1) の 計算を考えてみると、各クエリと似ているキーは、入力クエリと同じ値を持つキーになり、対応するバリューは結局入力したクエリになるという意味の分からない式になってしまいます。Multi-Head AttentionはLinear layerによって $Q, K, V$ を別々に変換するので、このような状況にならず入力系列間の関係性を学習することができます。

Positional Encoding

Multi-Head Attentionは系列の要素間の関係を学習することができますが、このままでは系列の順序まで考慮してくれません。そこで、Positional Encodingという手法で位置情報を入力へ足しこみます。

Position Encoding $PE$ は以下の式で与えられます。

$$\begin{aligned} PE_{\left(pos, 2i \right)} &= \sin \left(pos / 10000^{2i / d_{model}} \right) \\ PE_{\left(pos, 2i + 1 \right)} &= \cos \left(pos / 10000^{2i / d_{model}} \right) \end{aligned}$$

ここで、$pos$ は系列における位置（キーで例えるなら何番目のキーか）、$2i$ と $2i + 1$ は要素ベクトルの次元（キーで例えるなら $pos$ 番目のキーベクトルの何番目の要素か）を表します。[1] では、"The wavelength form a geometric progression from $2\pi$ to $10000 \cdot 2\pi$" と言っていることから、$0 \le 2i \le d_{model}$ であることがわかります。

式で考えるより、グラフを見た方がわかりやすいのでこちらをご覧ください。

グラフを出力するコードは本記事の最後に記載しました。さて、なぜこれで位置をエンコーディングできるのでしょうか。グラフを解剖していきましょう。

位置のエンコード

positionごとに値をいくつか取り出すと以下のようになっています。

位置が変わるごとにくびれている位置が変化していっていますね。くびれの位置を見ればどの位置かわかります。

次元のエンコード

なんと、系列の位置だけでなく次元までエンコードているのがPositional Encodingの凄いところ。次元方向に値をいくつか取り出すと以下のようになっています。

周期を見ればどの次元かわかるようになっています。

Add & Norm

Add & Normalization layerの略です。名前の通りskip-connection由来の入力を足して、Normalizationする層です。Transformerで用いられているようなskip-connectionはresidual connectionと呼ばれており、ResNetの思想を受け継いだ構造になっています。residual connectionを入れることでより深い層での学習を可能にしています。

Residual connection

residual connectionを知っている人は読み飛ばして大丈夫です。

ResNet登場以前はVGG16、VGG19やGoogLeNetなどが深い層を持つモデルとされていたのですが、せいぜい20層程度の深さが限界でした。当時、Batch normalizationの登場により勾配消失・爆発問題は防ぎやすくなっていたものの、これ以上層を深くすると性能が劣化（degradation）する問題があったためです（下図）。

[2] Figure 2より引用

ResNetではこのresidual blockを用いることで、100以上の層を持つモデルでの学習を可能にしました（下図）。

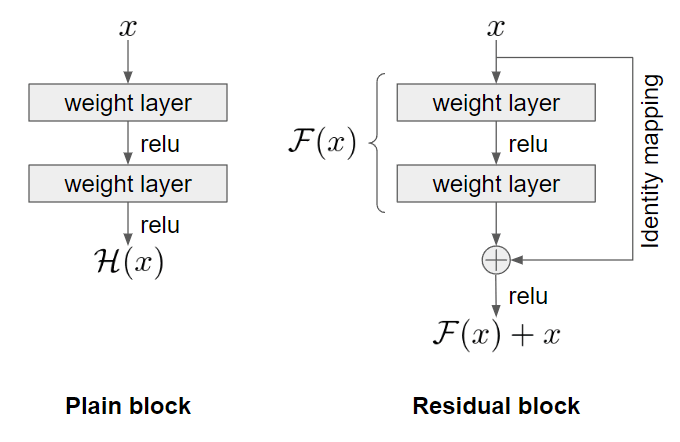
左が単なる直列のblock、右がresidual blockです。Identity mapping（恒等写像）が追加されただけですね。直感的理解としては、追加の層が不要でも $\mathcal{F}(x)$ が $0$ になれば良いだけなので層を深くしても問題ないということになります。

Layer Normalization

Normalizationにはlayer normalizationが用いられています（下図）。

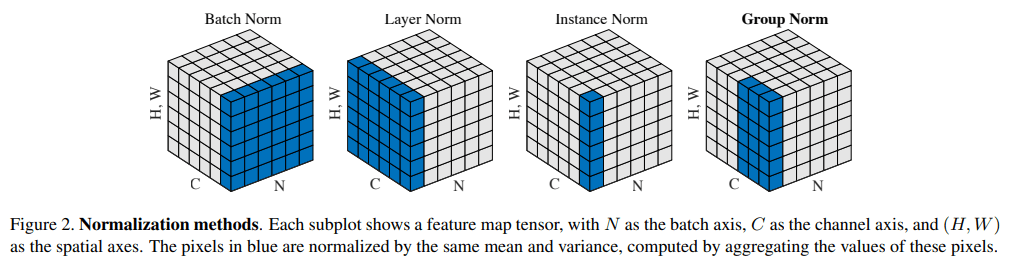
[3] Figure 2より引用

$N, C, H, W$ は順に、バッチサイズ、チャネル数、高さ、幅を表しています。画像が前提の説明なので $H, W$ がありますが、系列モデリングを前提としたTransformer では $H, W$ が系列の位置に相当します。この図では青のブロックの範囲でnormalizationをすることを示しています。

画像系から入ってきた人にはBatch Normalizationが馴染み深いと思うのですが、バッチサイズが小さいと値が不安定になる問題がありました。Layer Normalizationはバッチサイズに依存せず、一つのlayer内で正規化を行うことでこの問題を克服していることがわかると思います。

Feed Forward

図ではFeed Forwardとだけ書かれていましたが、[1]ではPosition-wise Feed-Forward Networksと呼んでいます。以下の式で与えられます。

$$\begin{aligned} \text{FFN}(\boldsymbol{x}) = \text{ReLU}(\boldsymbol{x}W_1 + \boldsymbol{b}_1)W_2 + \boldsymbol{b}_2 \end{aligned}$$

$\boldsymbol{x}$ が小文字であることに注意してください。position-wiseという名前の通り、系列の位置ごとに同一の関数を適用するということです（$W_1, \boldsymbol{b}_1, W_2, \boldsymbol{b}_2$ は各位置で共通ということです）。

まとめ

以上がTransformerを構成するブロックの全貌になります。Encoder、Decoder側でブロックを繰り返してやればTransformerの完成です（Decoder側2つ目のMulti-Head AttentionはEncoder側の $K, V$ を使用していることに注意）。

input/output embeddingやブロックの外のlinearはここでは説明していませんので悪しからず。Masked Multi-Head Attentionもここでは説明しませんでしたが、これは予測時に未来の情報がリークしないようにマスク処理が追加されたMulti-Head Attentionです。

付録

Positional Encodingのコード

import numpy as np
from numpy.typing import NDArray
import matplotlib.pyplot as plt
import seaborn as sns


def get_positional_encoding(pos: int, dmodel: int) -> NDArray[np.floating]:
    """Get positional encoding.

    Parameters
    ----------
    pos : int
        position
    dmodel : int
        dimension of the feature

    Returns
    -------
    pe : (dmodel,) NDArray[np.floating]
        positional encoding
    """
    pe = np.zeros(dmodel)
    pe_odd = np.arange(0, dmodel, 2)
    pe_even = np.arange(1, dmodel, 2)
    pe[pe_odd] = np.cos(pos / (10000 ** (pe_odd / dmodel)))
    pe[pe_even] = np.sin(pos / (10000 ** (pe_even / dmodel)))
    return pe


pe = np.vstack([get_positional_encoding(i, 100) for i in range(100)])
fig, ax = plt.subplots(1, 1, figsize=(12, 4))
sns.heatmap(pe, ax=ax, cmap="viridis")
ax.set_ylabel("position", fontsize=16)
ax.set_xlabel("dimension", fontsize=16)
ax.set_title("position encoding", fontsize=16)
plt.show()

参考文献

1. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L. & Polosukhin, I. (2017). Attention Is All You Need. arXiv. https://doi.org/10.48550/arxiv.1706.03762
2. He, K., Zhang, X., Ren, S. & Sun, J. (2015). Deep Residual Learning for Image Recognition. arXiv. https://doi.org/10.48550/arxiv.1512.03385
3. Wu, Y. & He, K. (2018). Group Normalization. arXiv. https://doi.org/10.48550/arxiv.1803.08494
4. ゼロから作るDeep Learning ❷ ―自然言語処理編 - 斎藤 康毅