フロントエンド開発で使う数理最適化
フロントエンド開発において、「数理最適化」という言葉を聞くことは少ないかもしれません。しかし、私たちが日々開発しているUIには、実は数理最適化で解決できる問題が潜んでいます。
フロントエンドにおける数理最適化の世界を覗いてみましょう!!
1. 地図UIの最適化問題
今回は、地図上に建物情報を表示するという実践的な課題を通じて、フロントエンドで数理最適化をどのように活用できるかを紹介します。
地図上の建物情報表示という実践的な課題
私の所属するスマサテ株式会社では、不動産情報を扱うサービスを展開しています。
不動産情報サービスや地域情報アプリでよく見かける、地図上に複数の建物マーカー(ピン)が表示され、それぞれの詳細情報がカードで表示されるUIを想像してください。ユーザーが地図を見たときに、どの建物がどの情報カードに対応しているかを直感的に理解できるよう、ピンとカードを線で結ぶ必要があります。
しかし、ここで問題が発生します。例えば20個の建物を表示する場合、 それぞれのカードをどこに配置すれば見やすいUIになるでしょうか? 適当に配置すると、以下のような問題が起きます:
- ピンとカードの接続線が長くなり、対応関係がわかりにくい
- 複数の線が交差して、スパゲッティのような見た目になる
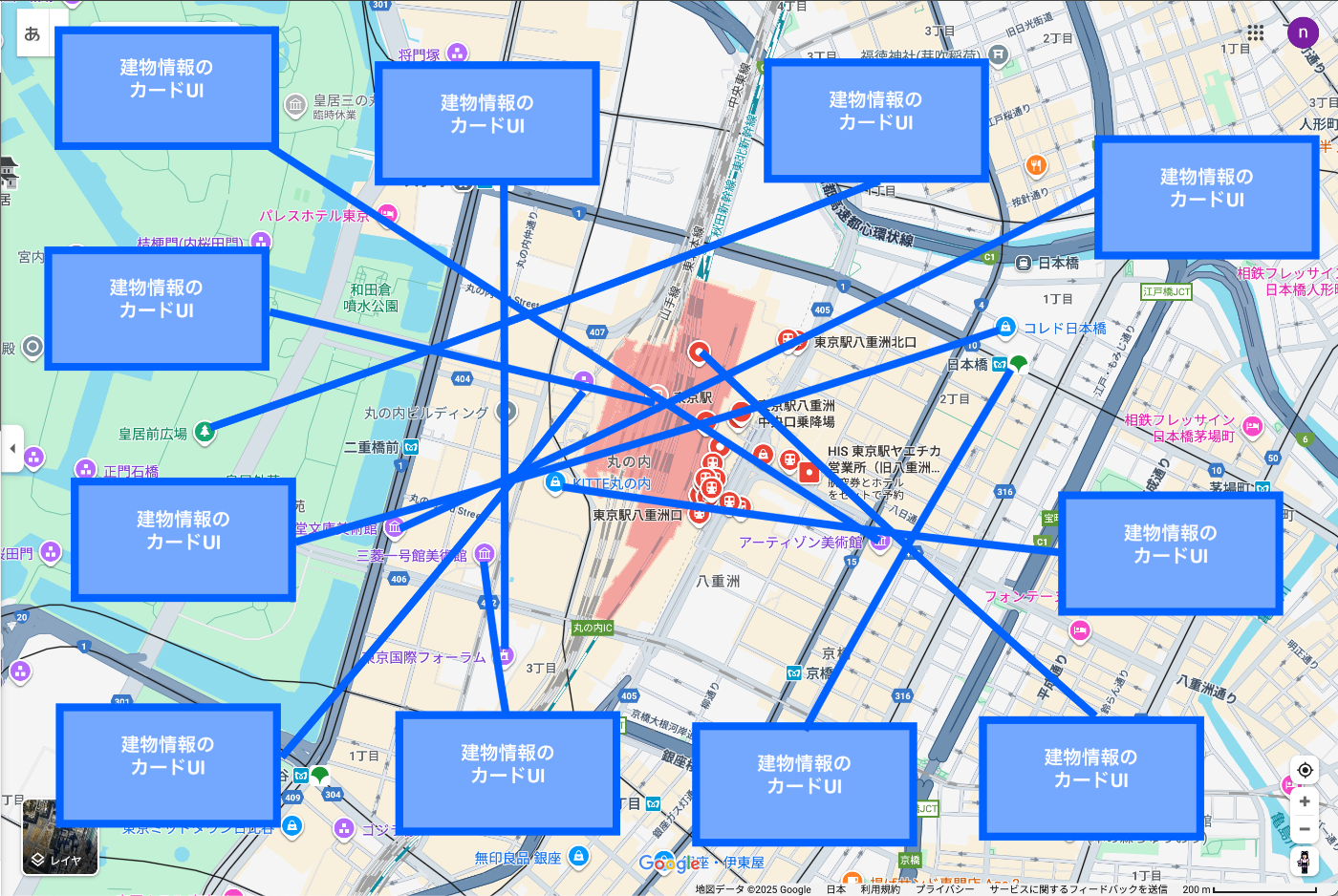
なぜフロントエンドで数理最適化が必要になったか
多くの場合、このような問題は「思いつきのいい感じのロジック」で解決されることでしょう。しかしそれには限界があり、配置パターン数が多い大規模なものになると、いい感じの配置になりません。
そこで、数理最適化が威力を発揮するわけです。
単純に数理最適化すればいいというものでもない
単純にやっていると、ブラウザの計算リソース(メモリやCPU)や所要時間の問題に突き当たるでしょう。現実的な時間内で最適化できなければなりません。
例えば20個の情報カードを表示する場合、20個のカードを20個のスロットに配置する組み合わせは 20! (20の階乗) = 約243京通りという天文学的な数になります。
愚直に最適化しようとすると、計算が重すぎてブラウザの挙動が停止してしまうでしょう。
つまりどうすればいいか
まず、以下を満たすように最適化問題に落とし込みます:
- ピンとカードの接続線の長さの合計がなるべく短くなる
- 複数の線がなるべく交差しない
そして、大域最適化(243京以上の中で最もいいもの見つけること) は諦めて、
計算が比較的軽く済む局所最適化を狙いましょう(限定した局所的な範囲で一番いいものを見つける) 。
2. 問題の定式化
先の章で述べたように目的関数は以下を反映したものになります:
- ピンとカードの接続線の長さの合計がなるべく短くなる
- 複数の線がなるべく交差しない
さらに、カードは地図の端(エッジ・コーナー)にのみ配置可能なものとしましょう。
(4コーナー + 上下各4スロット + 左右各4スロット = 計20スロット)
ここでいうスロットとは、「カードUIを配置可能な場所」を指しています。

すると以下のような数理最適化問題に定式化できます。
min f(x) = 接続線の長さの合計 + 1000 * 線の交差数
x in 約243京の配置
これは約243京の配置の中から f(x)を最小化するような配置xを見つける数理最適化問題です
これを愚直に解くととんでもない時間がかかるので、完璧な配置xを求めることを妥協しつつも、高速に解けるように工夫します。
3.問題の解法
ここで私が選んだのは、モンテカルロ法と2-opt法を組み合わせた2段階の解法です。
この解法はある程度高速で、ある程度いい配置を見つけることができます。
モンテカルロ法とは
一定数の解(ここでいうと配置x)をランダムに生成し、その中で最も良いものを採用する、という手法です。生成数を増やせば増やすほどいい解が得られる可能性が高くなるものの、実行時間は長くなります。
2-opt法とは
解の近傍(ここでいうと、2スロットのカード配置を交換することでできる配置全部)の中で最も良い解を見つけ出し、その解に対してまた同じことをする、というのを解が改善されなくなるまで繰り返すことで、初期解を改良した局所最適解を得る手法です。
モンテカルロ法と2-opt法の組み合わせ
以下のような流れでアルゴリズムが組まれます:
- まずモンテカルロ法で1000個の解を生成し、その上位50解を2-opt法の初期解とします
- 2-opt法で50個の初期解を改良した、50個の局所最適解を得ます
- 50個の局所最適解の中で最も優れている(つまりf(x)の値が小さい)解を実際の配置として採用します
4.TypeScriptでの実装
ここまでに説明したアルゴリズムを、実際にTypeScriptで実装していきます。ここでは、目的関数の実装、モンテカルロ法による初期解生成、First Improvement 2-opt法の3つの核心部分に焦点を当てて解説します。
ちなみに、コードが宣言的でなく可読性が不十分ですが、ここでは可読性よりも実行速度を重視しています。
また、関数や型の定義など一部のコードは省いているので、雰囲気で補完して読んでください。
目的関数の実装
まず、第2章で定式化した目的関数 f(x) = 接続線の長さの合計 + 1000 * 線の交差数 をコードに落とし込みます。
// 統合スコア関数(目的関数)
const calculateScore = (
assignment: Map<number, SlotPosition>, // 建物ID → スロット位置の対応
buildingPins: Map<number, PinPosition>, // 建物ID → ピン位置の対応
cardWidth: number,
cardHeight: number
): number => {
// 目的1: 接続線の長さの合計を計算
const totalDistance = calculateTotalLineLength(
assignment, buildingPins, cardWidth, cardHeight
);
// 目的2: 線の交差数を計算
const crossings = countCrossings(
assignment, buildingPins, cardWidth, cardHeight
);
// 距離と交差数の2つの目的を統合
// 交差1回 = 1000ピクセル分の距離と同等の悪さとして評価
const CROSSING_PENALTY = 1000;
return totalDistance + crossings * CROSSING_PENALTY;
};
モンテカルロ法による初期解生成
次に、1000個のランダムな配置を生成し、その中から上位50個を選び出す処理を実装します。
// モンテカルロ法による解の候補生成
const monteCarloSolutions: Array<{
assignment: Map<number, SlotPosition>;
score: number
}> = [];
for (let attempt = 0; attempt < MONTE_CARLO_ITERATIONS; attempt++) {
const assignment = new Map<number, SlotPosition>();
// Fisher-Yatesアルゴリズムでスロットをシャッフル
const shuffledIndices = Array.from({length: numSlots}, (_, i) => i);
for (let i = numSlots - 1; i > 0; i--) {
const j = Math.floor(Math.random() * (i + 1));
[shuffledIndices[i], shuffledIndices[j]] =
[shuffledIndices[j], shuffledIndices[i]];
}
// シャッフルされたスロットに建物を割り当て
for (let i = 0; i < assignmentSize; i++) {
assignment.set(buildingIds[i], slotsToUse[shuffledIndices[i]]);
}
// スコア計算して保存
const score = calculateScore(assignment, buildingPins, cardWidth, cardHeight);
monteCarloSolutions.push({assignment: new Map(assignment), score});
}
// スコア順にソートして上位50個を取得
monteCarloSolutions.sort((a, b) => a.score - b.score);
const topSolutions = monteCarloSolutions.slice(0, TOP_SOLUTIONS_COUNT);
ここでのポイントは、ランダムな配置を大量に生成することで、解空間を広く探索している点です。これにより、局所最適解に陥りにくい初期解を得ることができます。
First Improvement 2-opt法の実装
最後に、初期解を改善する局所探索アルゴリズムを実装します。通常の2-opt法との違いは、全ての近傍を探索せず、最初に見つかった改善解を即座に採用する点です。
const localSearch2Opt = (
initialAssignment: Map<number, SlotPosition>,
buildingPins: Map<number, PinPosition>,
options: PlacementOptions
): Map<number, SlotPosition> => {
const currentAssignment = new Map(initialAssignment);
let currentScore = calculateScore(
currentAssignment, buildingPins,
options.cardWidth, options.cardHeight
);
let improved = true;
// 改善できなくなるまで繰り返し
while (improved) {
improved = false;
const buildingList = Array.from(currentAssignment.keys());
// 全てのカードペアに対して2-optスワップを試行
outer: for (let i = 0; i < buildingList.length - 1; i++) {
for (let j = i + 1; j < buildingList.length; j++) {
const buildingA = buildingList[i];
const buildingB = buildingList[j];
// スロットを交換
const slotA = currentAssignment.get(buildingA)!;
const slotB = currentAssignment.get(buildingB)!;
currentAssignment.set(buildingA, slotB);
currentAssignment.set(buildingB, slotA);
const testScore = calculateScore(
currentAssignment, buildingPins,
options.cardWidth, options.cardHeight
);
if (testScore < currentScore) {
// 改善が見つかったら即座に採用
currentScore = testScore;
improved = true;
break outer; // 最初からやり直し
} else {
// 改善されない場合は元に戻す
currentAssignment.set(buildingA, slotA);
currentAssignment.set(buildingB, slotB);
}
}
}
}
return currentAssignment;
};
break outer; によって、改善が見つかった時点で内側と外側のループを両方抜けて、最初から探索をやり直します。これにより、First Improvement 2-opt法が用いられ、2-opt法に比べて計算時間を大幅短縮できます。
全体の統合
これらを組み合わせて、最終的な最適化処理は以下のようになります:
// 各上位解を起点としたFirst Improvement 2-opt局所最適化
let bestFinalAssignment = new Map<number, SlotPosition>();
let bestFinalScore = Infinity;
for (const solution of topSolutions) {
const improvedAssignment = localSearch2Opt(
solution.assignment,
buildingPins,
options
);
const finalScore = calculateScore(
improvedAssignment, buildingPins,
cardWidth, cardHeight
);
if (finalScore < bestFinalScore) {
bestFinalScore = finalScore;
bestFinalAssignment = new Map(improvedAssignment);
}
}
このように、モンテカルロ法で多様な初期解を生成し、それぞれに対してFirst Improvement 2-opt法で局所最適化を行うことで、高速かつ高品質な解を得ることができます。
5.さいごに
フロントエンドにおける数理最適化の実例をご紹介しました。一見難しそうな数理最適化も、適切に問題を定式化し、実用的なアルゴリズムを選択することで、ブラウザ上で十分高速に動作させることができます。
このような技術的チャレンジは、ユーザー体験を向上させる重要な要素です。皆さんのプロダクトにも、数理最適化で解決できる課題が潜んでいるかもしれません。
著者について
Hahnah こと 原井夏樹。
スマサテ株式会社所属のフルスタックエンジニアです。
参考になったら、"いいね❤️" と、Xをフォローしてくれると喜びます。
採用情報
弊社ではWebフルスタックエンジニア、AIエンジニアなどを積極的に採用しています。
ぜひ気軽にお話を聞きに来てください〜 お待ちしています!
Discussion