グラフ理論からPとかNP問題とかまでええええ
ごきげんようございます
さてさて、最近グラフ理論のさわりだけを勉強してみたんですがP問題とかNP問題とかにまで繋がったのでそこまで書いてみよーかなと思いました。ので書いてみます!!!Let's go!!!!
ooのさわりだけって慣用句ありますけどあれってセクハラの話ですか??
うわあああああ
そもそもグラフ理論とは一体なんのことでしょうか。まあ一言で言ってしまえば一筆書きみたいなところあるんですが、始まりは18世紀の初め頃にケーニヒスベルクの7橋問題という問題が、難しすぎるということで有名になり、そこであの天下のレオンハルト・オイラーが颯爽と現れて完璧に解いてみせたことにあるっぽいです。さすがオイラーさんですね。ちなみにオイラーさんは1703 - 1783にかけて天命を全うなさったということで、当時にしてはかなりのご長寿さんなんだなーと思いました。
がるるるるるる
そんなケーニヒスベルクの7橋問題を結構な時間かけて僕も考えてみたんですが、全然わかりませんでした。オイラー半端ないって、そんなんできひんやん普通と思いました。
ということで問題貼っておくので好きなだけ考えてみてください!歩きながら、ご飯食べながら、トイレ休憩しながら、気になるあの子を見つめながら、どんな時でもいいので考えてみてください!
以下のように7つの橋がかけられている。4つの陸地の任意の地点から(番号1−4)出発して、全ての橋(オレンジで表現しているもの)を、1度だけ通って出発地点に帰ってくることはできるか?できないならできないことを証明せよ

シンキングタイム
now thinking
now thinking
now thinking
now thinking
now thinking
now thinking
やるでええええ
さて、解けた方いらっしゃいますか ...?ほんとに初見プレイで解けた方いたらこんな記事読んでいる場合じゃないので、とりあえず近くの数学がわかる人に相談しましょう。あなたは必ず日本の宝になり得る存在です。一刻も早く、適切な環境に身をおくべきです。
解けなかった方は、こんな記事を読んでいても大丈夫です。あなたも凡人です。welcome to the real world!!まあまあ、そんな落ち込まなくてもいいじゃないですか。理想とのギャップを受け入れてから、人生動き出すみたいなとこあるやん?知らんけど。
まあまあ、話を戻すとオイラーはこれを数学的に解くために以下のように一般化しました。これがグラフ理論の始まりと言われているっぽいです。どうですか、これ。グラフ......なのか?てかグラフってなに?
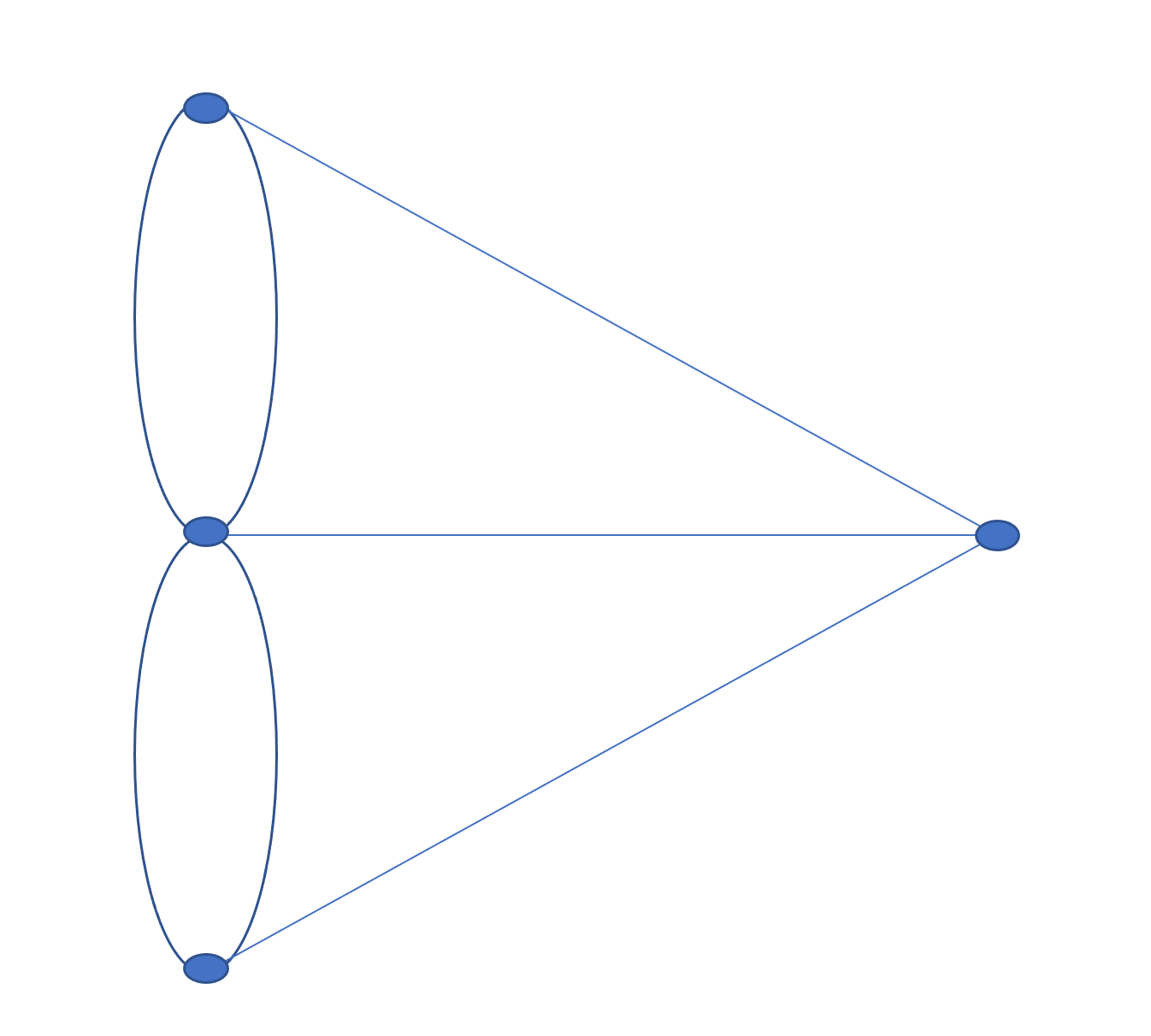
名前をつけてあげるよ。G(V,E)と書いてグラフと読もう
はい、こうしてグラフ理論の誕生につながったオイラーさんの話だったんですが、結局一般化してどないしてん?と読者の皆さんに思われてそうです。しかしながらちょいとお待ちを。あとで説明します。
ここでは、グラフ理論の基本的な定義を紹介いたします。
グラフGとは
・頂点もしくは、節(ノード)と呼ばれる点の集合Vと
・辺もしくは、エッジや枝と呼ばれる線の集合Eから成り立っている。
これをG(V,E)もしくはG=(V,E)とかく。
なお、Vは空集合ではなく、辺は頂点と頂点をつなぐものとする。
ほうほう、なるほど。要するに点と線の集合から成り立っているんですね。
では、次はそんな点と線の関係性についてみていきましょう。
グラフG(V,E)において、a,bがVの要素であり、eがEの要素であるとする。
・eがa,bをつなぐ辺である場合、a,bはeを介して隣接していると呼ぶ。同時にaとe,bとeは接続していると呼ぶ。
・eに向きがついていない場合は
- eは無向辺と呼ばれ
- a,bはeの端点と呼ばれる。
- e=(a,b)と表す。
・eに向きがついている場合は
- eは有向辺と呼ばれ
- a,bはそれぞれeの始点、終点と呼ばれる。
- e=<a,b>と表す。
- もしa=bの場合はeをループと呼ぶ
まあまあ、全て受け入れることのできるような定義ばかりで良かったです。
まあ他にもいくつかあるんですけど、ちょいちょい割愛させていただきつつ、上のに加えて次数については知っておかないと後ろがしんどいので次数について見ていきましょう。
任意の頂点vに対して、vに接続する辺の数をvの次数とよび、deg(v)と表す。
はい、おけです!点から生えている辺の数のことをグラフ理論では頂点の次数と呼ぶんですね。
ここまで来たらもうG(V,E)と書いてグラフと読めるはずです!!
オイラー再び
さてここでグラフ理論には以下のような定理があります。
グラフG(V,E)がオイラーサイクルを有するためにの必要かつ十分な条件はGの全ての頂点の次数が偶数であることである。
「・・・・・え!?!?!?!?まじで!?!?!?」
と僕は思いました。最高すぎるやろと。この定理を使えるならば(証明....)、頂点の次数を数え上げることで一筆書きができるかどうかわかるってことでしょ?つまりは、全てを一度通ってスタート地点に帰ってくることができるというルートが存在するかどうかも分かってしまうわけじゃないですか?(TSP出てきそうだな、おい。)
ということで最初の問題は、それぞれの次数を数え上げてみると、左の3つは上から3、5、3で右の1つだけの頂点は3なのでオイラーサイクルは持たないということになりますね。
えーと、おい定理出てきたのに証明がないぞ?という厳しいご意見もあるかと思いますが、必要条件までは分かったんです。
ただ十分条件の証明をしようとして心が折れたんです。。。それで許していただけませんか。。。
ちょいとお隣さん、あなたの家までの道を教えてよ
ということで、ここまででオイラーサイクル、すなわりグラフが与えられた際に、スタート地点から全てのルートを一度だけ通って戻ってくるルートが存在するかどうかはわかりました。しかしながら、じゃあそのルートぞいずこ?という疑問にぶち当たります。さて、どうしましょうか?人間がやる分には全ての組み合わせを図を見ながら網羅していけばいいでしょう。しかしながら、もし頂点が100個あったどうでしょうか?何なら10個くらいでもかなりしんどいと思います。tree書いてみても確認してみてもいいと思いますが、だいぶ面倒です。何が面倒かといえば、まだ通っていない道を通るという条件のもとで各頂点を順に追っていくことが面倒です。少し抽象度を上げると、繰り返し繰り返し考えて、記録していくことが面倒です。ということを考えていると内なる声が聞こえてきました。
「人間がやるのが面倒なら、PCがやればいいじゃない」
はい、了解です!じゃあ、アルゴリズム考えましょう!
しかしながら、確かにPCが繰り返し処理は大得意ですが、図を見ながらやるというのはとても苦手ですよね。なので、人間が図をみて行っていたことをどうにかして別の方法に変換しないといけない気がします。
そこで出てくるのが隣接行列です。隣接行列と聞くと最初は「うわっ」となってしまうんですが、実際にやってみるとなんてことはないので頑張りましょう。
たとえば以下のグラフについて考えてみましょう。
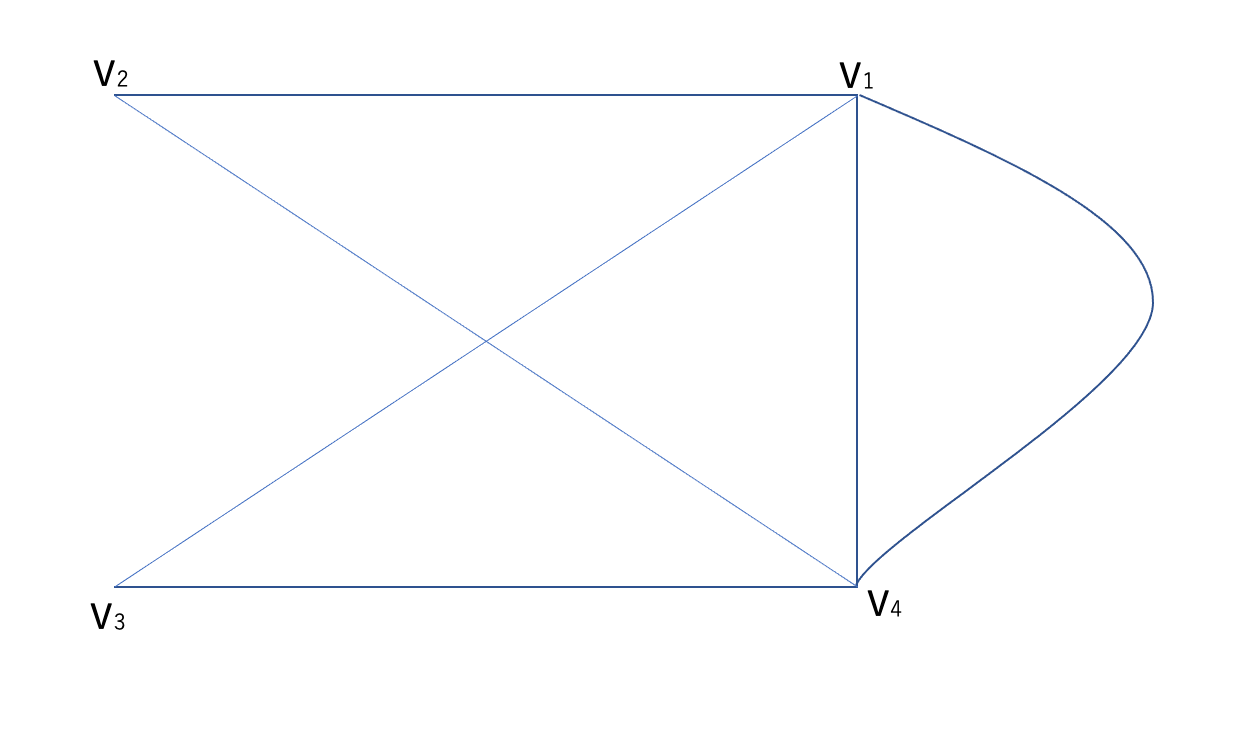
まず全ての頂点の次数を確認すると
v1:4, v2:2, v3:2, V4:4
となるので、オイラーサイクルを持つことがわかります。
ここで隣接行列とはを知るためにも定義をみてみましょう。
グラフ𝐺の頂点が𝑛個あるとき,頂点𝑣𝑖,𝑣𝑗を結ぶ辺の本数を𝑖𝑗要素に持つ𝑛次の正方行列のこと
ということらしいです。そして一旦やってみると隣接行列は以下のようになります。
さて、このままだとわかりにくと思うので何をやっているのか少しみてみますと、
i=1, j=1の時を考えた時には、頂点v1,v1を結ぶ辺の本数を11要素(1行1列目)に持たせることになるので、v1からv1に生えている辺の本数を数えます。すると0になるので、1行1列目に0を入れます。
次にi=1, j=2の時を考えた時には、頂点v1,v2を結ぶ辺の本数を12要素(1行2列目)に持たせることになるので、v1からv2に生えている辺の本数を数えます。すると1になるので、1行2列目に1を入れます。
次にi=1, j=3の時を考えた時には、頂点v1,v3を結ぶ辺の本数を13要素(1行3列目)に持たせることになるので、v1からv3に生えている辺の本数を数えます。すると1になるので、1行3列目に1を入れます。
・
・
・
を繰り返すと隣接行列が得ることができます。この行列をよくみると対称行列になっていることがわかりますね。まあ、v1->v2の辺の本数とv2->v1の辺の本数は同じはずなので「あ、そっか」と思ってもらえればいいじゃないかなと思います。そんなの考えるまでもないという厳しい意見もあると思いますが、許してください。。。
さて、とりあえずここまでで隣接行列を得ることができました。
このような形にまでグラフを落とし込めると、PCもやってやんよと思ってくれることでしょう。
せっかくここまでお越しくださったのだから、オイラーサイクルの見つけ方でもいかが?
さてオイラーサイクルを見つけるためには何をすればいいでしょうか?
人間が図を見ながらやっていたことは、総当たりでしたね。もちろんPCも同じです。
ということで今から総当たりをしていきます。
じゃあ、総当たりの試行を、隣接行列の操作に落とし込む必要があります。言葉を変えると、隣接行列に対してどのような操作をすれば、総当たりができるのか?といった感じですかね。
と、その前にさらっと隣接行列をおさらいしておくと、行がスタート地点、列が次に向かう頂点、要素が辺の数(=ルートの数)を表していましよね。
なので、v1からどこかの地点に移動できるためには、要素の数が1以上でないといけません。そして今はオイラーサイクルを考えているので同じルートは使えないので、例えばv1->v2に移動したらv2->v1のルートのうち、最初に使ったルートは使えないということを表現する必要があります。
このあたりに注意して考えると、以下のような操作になりそうです。
スタート地点の行の各列の要素を順番に見ていき、1以上であれば選択可能。そしてij要素を選んだ場合は、ij要素とji要素を-1して、j行目を見にいく。
ということを繰り返し、全ての要素が0になれば(0行列)終了。
はい、おけです!実際にやってみましょう!
私がおともして差し上げましょう
さっそく先ほどのグラフのv1からスタートしてみましょう。
v1からのスタートなので、ひとまず1行目の要素を見ていくと2,3,4列目はルートがあるようですね。
どれを選べばうまくいくのかはわかりませんが、ひとまず2列目に進んでみたいと思います。
はい、おけです!v1->v2に進んだので1行2列目を-1します。そしてv2->v1のルートも今使ったのでもう使えませんから、2行1列目も-1しておきましょう。そうすると上の行列が得られるわけです。
ちなみにpathとは道順のことなで、どのルートを辿ったかメモっておく程度の意味合いです。
さて、今はv2にいるので次は2行目をみます。すると、4列目以外はルートがないので、とりあえずv4に進んでみます。
すると、v2->v4のルートを辿ったので2行4列目と4行2列目を-1します。すると上のような行列が得られます。では今はv4にいるので、4行目をみてみると1列目と3列目はいけそうですね。うーん、初めて2という数字を選んでみましょうか。ということでv1に移動してみたいと思います。
どうですか?だいぶ慣れてきましたか?今はv4->v1のルートを辿ったので4行1列目と1行4列目を-1しました。すると上のような行列が得られます。では今はv1にいるので、1行目をみてみると3列目と4列目でまた迷うわけです。あえて4列目を選んでみましょう。せっかくv4から移動してきたわけですが、また戻ってみます。
すると、3列目しかいくとこないのでv4->v3の移動をしてみます。
最後に、1列目しかいくとこないのでv3->v1の移動をすると
こうして無事に0行列を得ることができましたし、ルートを確認してみると重複もなさそうで、オイラーサイクルを得ることに成功しました!!1
とはいえ、実際にこんなにうまくいくことはそんなにないかと思いますので、0行列を得られるような組み合わせが出てくるまで、今のやり方を繰り返し行うという考え方でいてくださいね。
あらやだ、まさかこんなところで出会うんて!ねぇ、ハミルトンさん!
ということで、オイラーサイクルって何?存在するかどうかってわかるの?存在するならどうやってルートを見つけるの?というところまではなんとか、天才・オイラーによって定められた定理などによって理解することができました。ところが、なんと新たな天才・ハミルトンによってこんなグラフはあるのだろうか?と提案されました。どのようなルートを考えるかといえば
すべての点を1度だけたどって元に戻れるようなルート(回路)
むむむ、全ての点を通れば全ての辺を通ることになって、ハミルトンサークルとオイラーサークルって同じなんじゃないの?と思ったそこのあなた!実はそうではないグラフもあるんです!以下のグラフをご覧ください!

こちらのグラフで外側の辺だけを通るとハミルトングラフになりはしませんでしょうか!?
ハミルトンさんはいつもどこにいらしてますの?
さてそういえば、オイラーサイクルでは判定方法や探索方法が確立されていました。ハミルトングラフについてはどうなんでしょうか?
探索方法についてはあるっぽいんですがよくわかりませんでした。。。一方判定方法に関しては、十分条件を満たす、Diracの定理とそれを少し拡張したようなOrreの定理というものは見つかっているものの必要十分条件は見つかっていないようです。
言い換えると、Orreの定理を満たせばハミルトンサークルを持つと判定できるのですが、Orreの定理をみたさないからといって、ハミルトンサークルを持たないとはいえないということです。
なのでOrreの定理を満たさない場合は一気に難問になります。一応2つほど試してみる価値のあるやり方はあるっぽいですが、このケースバイケースに判定方法を見つける(見つけられるなら)ような感じがします。。。
そんなハミルトンサイクルなんですが、問題の複雑性からNP問題という部類に割り振られています。
そろそろ、みなさんいい頃合いでしょう?
ここまでなんとかたどり着いたので最後にNP問題とかP問題とかの話をしてみようと思います。
何かしらの問題の解を求める際には、その問題の特性を分析するのが一般的だと思います。
それは計算機科学の分野でも同様で、こちらの分野では問題の複雑性に着目してカテゴライズしています。大まかには3つほどに分かれていてこんな感じです。
とその前に、多項式アルゴリズムについて知っておかないと辛いんでまずはそちらからどうぞ。
定数kを用いて、時間計算量がO(n^k)のアルゴリズムを多項式アルゴリズムと呼ぶ
そしてそれを踏まえてどうぞ。
タイプ1:問題を解くために利用できる多項式アルゴリズムが存在することを保証できる問題
タイプ2:多項式アルゴリズムでは解けないことを証明できる問題
タイプ3:問題を解くための多項式アルゴリズムを見つけることが不可能であることも証明できない問題
なんか色々すごいっすね。。。解けないことを証明できるんですね。。。。
そして、上でみたことは、複雑性の種類を3パターンに分けただけなので、この種類を用いて計算機科学の分野で定義されている問題についてみてましょう。
すると、真っ先に出てくるのがNP問題とP問題です。それぞれ以下の通りです。
NP問題に分類されるための条件:
候補解が最適解であることを証明するために利用できる多項式アルゴリズムが存在する。
P問題に分類されるための条件:
NP問題に分類されるための条件に加えて問題を解くために利用できる多項式アルゴリズムが1つ以上存在していることが保証されている。
ということらしいです。なので複雑性の観点から見るとP問題はタイプ1に分類することができそうで、さらにNP問題に包含されるということになります。
さらにさらに、あと二つほど定義されている問題があるので続きをどうぞ。
NP完全に分類されるための条件:
・候補解を生成するための既知の多項式アルゴリズムが存在しない。
・候補解を最適解であることを証明するための既知の多項式アルゴリズムが存在する。
NP困難に分類される問題:
NP問題に分類される問題と同じくらい難しいものの、NP問題に分類する必要がない問題
なるほど、難しいなぁ。とりあえずNP困難は調整役みたいな扱いなんですね。
まとめるとこんな感じかな。
NP問題の中にP問題とNP完全が含まれていて、NP完全とP問題は独立。NP困難はNP問題と独立っぽいけど難易度的にはNP問題に含まれてもいいわけだから、部分的に被っている感じ
図にするとこんな感じ?ちょっとでもわかんないNP完全とかNP困難の扱いがわかりません。。。

もう疲れぽよよよーん
色々とみてきたわけですけども、やはりどの分野においても、課題というものが存在していて、それをどのようにカテゴライズするかに関して統一を取るために上記のような定義をしているんだろうなと思います。上記のようにカテゴライズすることで計算機科学が発展しやすいのかどうかに関しては色んな事象や経験を積んでいくことで、検証していきたいなと思ってます。
ちなみにP=NPかどうか?というのは未解決問題らしくて、解けたら100万ドルもらえるらしいっすよ。
しかも今円安なんでドルを円に変えたら1億円以上もらえやす!!!
まあそんな話は縦おき、毎回1、2時間くらいで終わるなーと思って勢いよく描き続けて、チョコチョコ調べて、気付いたらかなり時間が経っているみたいなことをポリリズムしているんですが、これは一体なぜ。。。僕にとってのNP困難ですねぇ。。。。。
Discussion