✏️

ベイズ統計学・学習メモ

2024/04/21に公開

ベイズ統計

tech

ベイズ推論とは

ベイズの定理による帰納的学習の過程

帰納的学習：ある集団の一般的な特性（パラメータ $\theta$ ）について
　　　　　　その集団の一部（ $y$ ）を用いて学習すること

ベイズ法：ベイズ推論の原理から導出されたデータ分析のツール

統計的に望ましい性質を持つパラメータの推定量
観測されたデータの簡潔な記述
欠損データの予測、将来のデータ予測
モデルの推定、選択、検証のための枠組み

ベイズの定理

$p(\theta|y) = \frac{p(y|\theta)p(\theta)}{\smallint_\Theta p(y|\theta)p(\theta)}$
$p(\theta)$ ：事前分布
　→　 $\theta$ が母集団の特性を表していると、我々がどれだけ信じているか
$p(y|\theta)$ ：標本モデル・統計モデル・尤度関数・カーネル
　→　 $\theta$ が真の値なら、 $y$ が結果になるとどれだけ信じているか
$p(\theta|y)$ ：事後分布
　→　 $y$ を観測した後に、 $\theta$ が真の値だとどれだけ我々が信じているか
$\smallint_\Theta p(y|\theta)p(\theta)$ ：エビデンス・事後分布の規格化定数
　→　確率の総和は1になるので、事後分布がそうなるようにするための定数

ベイズ統計の流れ

下調べ（問題の背景を調べる）
原因と結果の関係の仮説を立てる
統計モデル（標本モデル、尤度関数、カーネル）を作成
0をもとに統計モデルを作る
事後分布の計算
得られたデータから事後分布を推定する

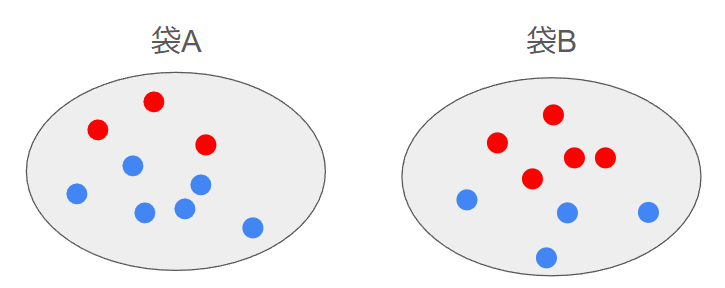
ex) 2つの袋があり、どちらかの袋から4回復元抽出をしたところ{青、青、赤、青}という結果が得られた。この時、袋Aが選ばれた確率はいくらか。
　Yが赤・青の球を引く事象、Xが袋A・Bを選ぶ事象。

下調べ
ここで、袋Aのほうが若干選ばれやすいこと、それぞれの袋に青・赤の球がどれだけ入っているかは知っている。
　　 $p(X=a)=0.6, p(X=b)=0.4$ とする。
統計モデル（標本モデル、尤度関数、カーネル）を作成
通常は未知である。〇〇分布に従うとかで定義する。
$p(Y=r|X=a)=0.3$
$p(Y=b|X=a)=0.7$
$p(Y=r|X=b)=0.56$
$p(Y=b|X=b)=0.44$
事後分布の計算
この例だと手計算だが、通常はMCMCをよく使う。
$p(\theta|y) = \frac{p(y|\theta)p(\theta)}{\smallint_\Theta p(y|\theta)p(\theta)}$ より計算していく。
X=aの時は
$p(y={b,b,a,b}|X=a)p(X)=0.7*0.7*0.3*0.7$
=0.0617
X=bの時は
$p(y={b,b,a,b}|X=b)p(X)=0.44*0.44*0.56*0.44$
=0.0195
事後分布の規格化定数は
$\smallint_\Theta p(y|X)p(X)$ = 0.0617+0.0195
よって事後分布は
$p(X=a|y={b,b,a,b}) = \frac{0.0617}{0.0617+0.0195}$
=0.76

ベイズ更新

自然共役事前分布

※イメージ
　
という風に見ると、事後分布の形=事前分布の形となっている！
これが成り立つ事前分布を自然共役事前分布という。
以下、その例だがすべて覚える必要はなく、出てきたときに調べればよし。

確率分布	共役事前分布	事後分布
ベルヌーイ分布	ベータ分布	ベータ分布
二項分布	ベータ分布	ベータ分布
正規分布( $\sigma$ 既知)	正規分布	正規分布
正規分布( $\sigma$ 未知)	逆ガンマ分布	逆ガンマ分布
ポアソン分布	ガンマ分布	ガンマ分布
多項分布	ディリクレ分布	ディリクレ分布

何がいいのか？
　→　事後分布がベイズ更新のたびに複雑になることがない！

事後分布の推定

事後分布の推定方法には3つある。
①共役事前分布を用いて手計算(ただしパラメータが2つ以上あると難しい)
②MAP推定(確率分布全体を求めるのは諦め、代わりに事後分布の密度が最大になる点を求める)
③MCMCで事後分布をサンプリングする

共役事前分布を用いて手計算

例として、二項分布を考える。
二項分布は成功確率 $\theta$ で成功か失敗のいずれかの結果となる試行（ベルヌーイ試行と呼ばれる）を独立に n 回行ったときの成功回数を確率変数Xとする離散確率分布。
二項分布の共役事前分布はベータ分布で、事後分布もベータ分布。
$binomial(x|\theta) = _nC_x\theta^x (1-\theta)^{n-x}$
$Beta(x|\alpha, \beta) = \frac{1}{B(\alpha, \beta)}\theta^{\alpha -1}(1-\theta)^{\beta-1}, (B(\alpha, \beta)=\smallint^1_0 t^{\alpha-1}(1-t)^{\beta-1}dt)$
事後分布を計算してみると
$p(x|\theta) = p(\theta|x)p(x) \propto \theta^x (1-\theta)^{n-x} \frac{1}{B(\alpha, \beta)}\theta^{\alpha -1}(1-\theta)^{\beta-1}$
$p(x|\theta) \propto \theta^{\alpha+x-1} (1-\theta)^{\beta+n-x-1}$
$\alpha' = \alpha+x, \beta' = \beta+n-x$ と置けば、
$p(x|\theta) \propto \theta^{\alpha'-1} (1-\theta)^{\beta'-1}$ → 事後分布がベータ分布になった！

ex)
コインを弾いたとき、表が出る確率を推定する問題を考える。
前提として、コインは歪な形をしており、どんな確率で表がでるか見当もつかなそうだ。
例えばコインを10回弾いて表が6回出た。

まず、事前分布を設定する必要がある。
ベータ分布はαとβの値によって、その形が変わるのだが、 $\alpha = 1, \beta = 1$ とすると、これは一様分布となる。
つまり、どの確率をとる確率も一定ということになる。
　→　コインを弾いたらどんな確率で表がでるか見当もつかなそうだ、という事前の信念をこれで表すことができる。

そして、実際に当てはめてみると、
$\alpha' = 1+6, \beta' = 1+10-6$
$p(x|\theta) \propto \theta^{7} (1-\theta)^{5}$ となる。

別の試行で、30回弾いて18回表が出た場合も確認してみると、
$\alpha' = 1+18, \beta' = 1+30-18$
$p(x|\theta) \propto \theta^{19} (1-\theta)^{13}$ となる。

手計算で事後分布を計算する例と、事前共役分布を用いると簡単にそれが求まることが分かった。

MAP推定(事後分布の密度が最大になる点の推定)

MAPとはmaximum posterior pointの略で、事後分布の密度が最大になる点のこと。
つまり、 $\theta_{MAP} = argmax_{\theta} p(\theta|y)$

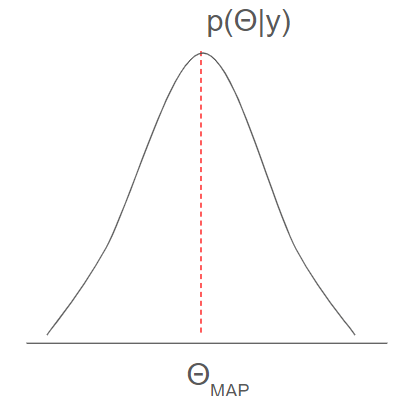
事後分布からMAP推定をする。
$p(\theta|y) \propto p(y|\theta)p(\theta)$ であるが、ここで、 $p(\theta)$ に無情報事前分析を用いる。これは $normal(\theta|0, 100)$ のような分布である。これは事後分布に影響を及ぼさない広い範囲で一定な分布である。
そのような時、
$\theta_{MAP} = argmax_{\theta} p(\theta|y)$
$\theta_{MAP} = argmax_{\theta} p(y|\theta)p(\theta)$ ここで、 $p(\theta)$ は一定とみなすと、
$\theta_{MAP} = const. argmax_{\theta} p(y|\theta)$ となる。
この最後の項は、最尤推定と同じ（無情報事前分布を用いたら最尤推定値とMAP推定値は一致する）。

MCMCで事後分布のサンプリング

先ほどまでは、手計算で何とか事後分布の情報を計算してきたが、実際問題として共役事前分布がすべての事前分布を表せるわけではない。また、パラメータが多い複雑な統計モデルとなるとこれらは難しい。そこで、MCMCが出てくる。これを使うと一般的な統計モデルの事後分布からパラメータをサンプリングできる。