🐊

【R】群逐次デザインの理論と実装

に公開
R
臨床試験
gsd
中間解析
tech

臨床試験デザインに関する学習記事です。群逐次デザイン（Group Sequential Desig、GSD）の枠組みを数式と実装から理解することが目標です。

1. 理論

1-1. 概要

群逐次デザインは、臨床試験の途中で複数回の中間解析を計画的に行い、早期終了（有効性、無益性、安全性）やサンプルサイズ再設定を可能にするデザインです。中間解析を複数回行うと、第一種の誤り（\alphaエラー）が累積するため、全体の\alphaエラーを事前に決めた値以下に抑える必要があり、これを実現するのが、\alpha消費関数です。

1-2. \alpha消費関数

t_k = \frac{I_k}{I_{\text{max}}}
  • t_k : 試験で得られる全情報量のうち、観測されている情報量の割合
  • I_k : k回目の中間解析時点の情報量（例：症例数、イベント数）
  • I_{\text{max}} : 最終解析時点の情報量
\Delta\alpha_k = \alpha(t_k) - \alpha(t_{k-1})
  • \alpha(t) : 情報割合tまでに累積して消費した\alphaエラーの合計
  • \alpha(t_k) : k回目の中間解析までに累積で消費した\alphaエラーの量
  • \alpha(t_{k-1}) : 前回の中間解析までに消費した\alphaエラーの量
  • \Delta\alpha_k : k回目の中間解析で新たに消費する\alphaエラーの量

1-3. 代表的な\alpha消費関数

1-3-1. O'Brien-Fleming型

\alpha(t) = 2 \left[1 - \Phi\left(\frac{z_{1-\alpha/2}}{\sqrt{t}}\right)\right]
  • \Phi(\cdot) : 標準正規分布の累積分布関数
  • z_{1-\alpha/2} : 標準正規分布の上側\alpha/2点

1-3-2. Pocock型

\alpha(t) = \alpha \cdot \log\left(1 + (e-1)t\right)

1-4. 停止境界

b_k = z_{1-\alpha_k}
  • b_k : k回目の中間解析で、検定統計量Z_kがこの値を超えたら試験を早期終了するという閾値
  • z_{1-\alpha/2} : 標準正規分布の上側\alpha_k点

2. R実装

2-1. \alpha消費関数を定義

obrien_fleming_alpha <- function(t, alpha = 0.05) {
  z <- qnorm(1 - alpha / 2)
  2 * (1 - pnorm(z / sqrt(t)))
}

pocock_alpha <- function(t, alpha = 0.05){
  alpha * log(1 + (exp(1) - 1) * t)
}

2-2. \alpha消費関数のデータフレーム作成

info_frac <- seq(0.1, 1, by = 0.01)
df_alpha <- bind_rows(
  tibble(
    info_frac = info_frac,
    alpha_spent = obrien_fleming_alpha(info_frac),
    method = "O'Brien_Fleming"
  ),
  tibble(info_frac = info_frac,
         alpha_spent = pocock_alpha(info_frac),
         method = "Pocock"
  )
)

2-3. \alpha消費関数の可視化

ggplot(df_alpha, aes(x = info_frac, y = alpha_spent, color = method)) +
  geom_line() +
  labs(title = " alpha spending function",
       x = "information rate",
       y = "cumulative alpha spent",
       color = "method") +
  theme_minimal()

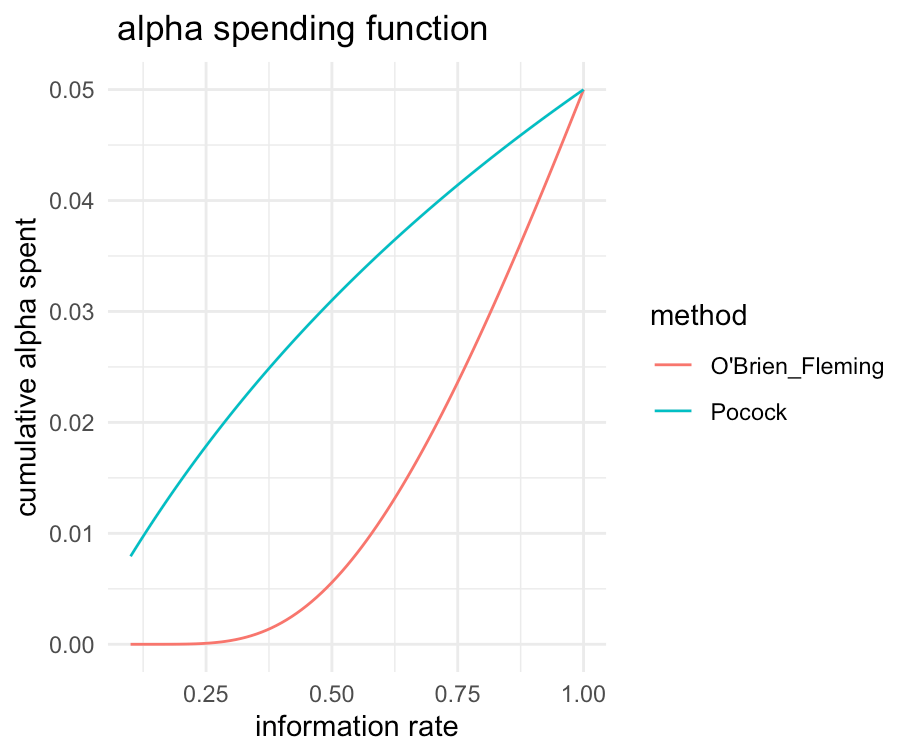
  • O'Brien-Fleming法は、初期の情報割合でほとんど\alphaを消費せず、最終解析に近づくほど\alpha消費が増える。
  • Pocock法は、各解析で均等に\alphaを消費する。

2-4. 停止境界の計算と可視化

info_points <- c(1/3, 2/3, 1)
alpha_obf_points <- obrien_fleming_alpha(info_points)
alpha_pocock_points <- pocock_alpha(info_points)

z_obf <- qnorm (1 - alpha_obf_points)
z_pocock <- qnorm(1 - alpha_pocock_points)

df_boundary <- tibble(
  interim = rep(1:3, 2),
  info_flaction = rep(info_points, 2),
  z_bound = c(z_obf, z_pocock),
  method = rep(c("O'Brien-Fleming", "Pocock"), each = 3)
)

ggplot(df_boundary, aes(x = info_flaction, y = z_bound, color= method)) +
  geom_point() +
  geom_line() +
  scale_x_continuous(breaks = info_points) +
  labs(title = "stopping boundary",
       x = "information rate",
       y = "stopping boundary",
       color = "method") +
  theme_minimal()

  • \alpha消費量は「その中間解析で、帰無仮説が本当なのに有意差が出てしまう（偽陽性）確率」のこと。
  • Z値が高いほど、標準正規分布の上側確率（\alpha消費量）は小さくなり、判定が厳しくなる。
  • O'Brien-Fleming法は「初期解析で厳しい判定」、Pocock法は「どの回も同じ判定基準」。

2-5. 感度分析：\alphaを変えて\alpha消費関数を可視化

alpha_levels <- c(0.01, 0.05, 0.1)
df_alpha_sensitivity <- map_dfr(alpha_levels, function(a){
  tibble(
    info_frac = info_frac,
    alpha_spent = obrien_fleming_alpha(info_frac, alpha = a),
    alpha_level = paste("alpha =", a)
  )
})

ggplot(df_alpha_sensitivity, aes(x = info_frac, y = alpha_spent, color = alpha_level)) +
  geom_line() +
  labs(title = "O'Brien-Fleming(alpha sentivive analysis)",
       x = "information rate",
       y = "cumulative alpha spent",
       color = "alpha levels") +
  theme_minimal()

3. 終わりに

間違いなどありましたら遠慮なくご指摘いただけますと幸いです。

Discussion