株式会社 STAR AIPublicationへの投稿
😺

広告配信を賢くする多腕バンディット問題の考え方

STAR AIメンバー
に公開
マーケティング
強化学習
バンディット問題
効果検証
zennfes2025free
tech

多腕バンディット問題について

初めまして、株式会社STAR AIでエコノメトリストとして活動しています長谷川です。今回は、機械学習の中でもやや扱われる機会の少ないバンディット問題に焦点を当てて、実際の広告配信などのユースケースを見据えながら説明をしたいと思います。

序論

多腕バンディット問題とは

多腕バンディット問題とは、限られた試行回数の中で、複数の選択肢から報酬を最大化するための最適な選択戦略を学習する問題です。強化学習の一分野として扱われることもあります。例えば、広告の配信問題において、対象のユーザーにどの広告を配信すれば、クリック率を最大化できるかというような問題に用いられます。

この問題では、まだ試したことのない選択肢にチャレンジする「探索（exploration）」と、これまでの経験から有望だと分かっている選択肢を繰り返す「利用（exploitation）」のバランスを取ることが求められます。「探索」しすぎれば無駄が増え、「利用」しすぎれば最適解を見逃すリスクがあります。

多腕バンディット問題は、Web広告の最適表示、レコメンドシステム、A/Bテスト、自律型IoT制御など、現実の意思決定場面で幅広く応用先があります。特に動的な環境で、フィードバックを得ながら最適な行動を学習する必要がある場面に適しています。

代表的な解法には、ランダムに探索する「ε-貪欲法」、信頼区間を活用して探索する「UCB法」、報酬の期待値に従い探索を行う「確率一致法」などがあります。このブログでは、多腕バンディット問題について、どのようなことをしようとしているか、どう定式化・解決するかについて説明します。

多腕バンディット問題（確率的バンディット問題）の定式化

多腕バンディット問題には複数の定式化が存在しますが、最もベーシックなものが確率的バンディット問題の定式化です。ちなみに、その他の定式化には、敵対的バンディット問題というものがあり、自身の方策を知っている敵対者がいるものとして、そのもとで自身の報酬を最大化します。敵対的バンディット問題は、囲碁や将棋などのゲームを扱う際にも用いられます。

確率的バンディット問題の定式化要素は以下のようになります。

  • 選択肢（アーム）: 意思決定者が選択可能な（K個の）行動の選択肢です。これを「アーム」とも呼び、ここでは \mathcal{A} = \{1, 2, \ldots, K\} と表記します。
  • 時間軸: t = 1, 2, \ldots, T で表される離散的な時間ステップの系列。Tは総試行回数です。
  • 報酬分布: 各アーム a \in \mathcal{A} には、未知の確率分布 χ_a が関連付けられています。各時刻 t においてアーム a_t が選択されると、報酬 X_{a_t, t} が過去の履歴とは独立に分布 χ_{a} から抽出されます。
  • 期待報酬: 各アーム a の期待報酬を \mu_{a} = \mathbb{E}[X_a] とします。この期待値は意思決定者には未知です。
  • 最適選択肢: 最も高い期待報酬を持つアームを a^* とし、その期待報酬を \mu^* = \max_{a \in \mathcal{A}} \mu_a と定義します。

意思決定者の目的は、過去の観測履歴に基づいて選択肢 a_t を選択する方策を設計し、時間軸の終点Tまでの累積報酬を最大化することです。すなわち、

\max_{a_1,a2,… , a_t} \; \sum_{t=1}^{T} \mu_{a_tt}

を達成することが目標となります。


性能評価の指標：リグレット最小化

多腕バンディット問題を解くために、「リグレット（regret）」を損失関数のようなものとして定義します。リグレットは、各ステップで最適な選択肢を選ばなかったことによる機会損失と等価で、レグレットを最小化することで、最適な選択肢を選ぶモデルを作成します。時刻 T までの累積リグレット R_T は、常に最適アーム a^* をプレイし続けた場合の累積報酬と、実際の方策による累積報酬との差の期待値として定義されます。

（期待）リグレット

R_T = \mathbb{E}\left[\sum_{t=1}^{T} \mu^* - \mu_{a_t t}\right]



アルゴリズムの目標地点：理論限界（リグレット下界）

多腕バンディットアルゴリズムのゴールは、「リグレットをゼロにする」ことではなく、できる限り少ないリグレットとなるように学習することです。

理論的に最善なのは、リグレットが O(\log T)（＝時間の対数に比例する）程度で済むようなアルゴリズムであることが知られています。この理想に近づけるアルゴリズムは、「漸近的に最適」と呼ばれています。

より形式的には、リグレットは以下の下界を満たします。

{R}_T \ge \frac{\log T}{D_{KL}(\mu_a || \mu_{a^*})}

ここで、D_{KL} は報酬分布間のカルバック・ライブラー（Kullback-Leibler）ダイバージェンスです。理論限界は、極めて重要な指標で、不確実性の下で学習するためには、ある程度のリグレットの発生が不可避であること、リグレットは完全になくすことはできないが、うまく設計されたアルゴリズムなら、その増え方を非常にゆるやか（O\log T）に抑えられることを教えてくれます。

これは、効率よく学習するための理論的な限界と目標を教えてくれる重要な指針です。

多腕バンディットアルゴリズムの比較

多腕バンディットアルゴリズムには、主要な手法として、ε-貪欲法、UCBアルゴリズム、確率一致法などがあります。簡単にそれぞれのアルゴリズムを比較してみましょう。

ε-貪欲法 (ε-Greedy Algorithm)

ε-貪欲法は、εを設定し、N回中の最初のεN回までは探索期間として全ての選択肢を一様に探索し、その後の（1-ε）N回については、平均報酬が最も高い選択肢を利用するというアルゴリズムです。

  1. N回の試行をするものとする。
  2. εN回まで K 個の全選択肢の中からランダムに1つを選択する。
  3. その後（1-ε）N回は、εN回目までに観測された平均報酬が最も高い選択肢を選択する。

ここでは、パラメータ \epsilon \in (0, 1) の設定が、探索と活用のバランスを制御します。

ε-貪欲法では、εを調整することで理論限界を達成できますが、εの調整は普通は難しく、未知の背景情報を必要とします。ただし、ε-貪欲法は実装が簡単なのでよく用いられます。

以下は、ε-貪欲法を実行してリワードを返すPython関数のコード例です

def epsilon_greedy(bandit, epsilon, N):
    k = bandit.k
    rewards = np.zeros(N)     # 各ステップの報酬を記録
    counts = np.zeros(k)      # 各腕を引いた回数を記録
    values = np.zeros(k)      # 各腕の推定報酬（平均報酬）を記録

    # 最初のε*N回はランダムに探索
    explore_rounds = int(epsilon * N)
    for t in range(explore_rounds):
        arm = np.random.choice(k)  # ランダムに腕を選ぶ
        reward = bandit.pull(arm)
        counts[arm] += 1
        # 報酬を更新（移動平均）
        values[arm] += (reward - values[arm]) / counts[arm]
        rewards[t] = reward

    # 残りの回数は、常に最も価値が高い腕を選ぶ（活用）
    for t in range(explore_rounds, N):
        arm = np.argmax(values)    # 推定報酬が最大の腕を選ぶ
        reward = bandit.pull(arm)
        counts[arm] += 1
        values[arm] += (reward - values[arm]) / counts[arm]
        rewards[t] = reward
        
    return rewards

UCBアルゴリズム (Upper Confidence Bound)

UCBは、報酬の分布に関して信頼区間を設定し、信頼区間の中で最悪の場合を想定して選択肢を選ぶ手法です。各時刻 t において、以下のスコアを最大化する選択肢（アーム） a を選択します。

\bar{\mu}_{a}(t) = \hat{\mu}_{a}(t) + \sqrt{\frac{ \log t}{N_a(t)}}

ここで、\hat{\mu}_a(t) は時刻 t までのアームaの平均報酬、N_a(t) はアーム a の選択回数、t はこれまでの試行回数です。 第1項は既知の選択肢の探索結果による活用を促し、第2項は試行回数が少ない選択肢の探索に取り組みます。各腕の推定価値に、その腕が引かれた回数が少ないほど大きくなる「信頼上限」を加味して、次に引く腕を決定します。これにより、不確実性が高い（あまり試行されていない）腕を積極的に探索するようになります。

UCBのリグレットは O(\log T) のオーダーであることが証明されており、理論限界と整合するので、ある程度多くの試行をする場合には良好なアルゴリズムです。一方で、UCBでは、本来は期待値最大である可能性が小さい選択肢にも多くの探索を行ってしまう欠点があります。

以下は、UCBアルゴリズムのPythonコードです。

def ucb(bandit, N):
    k = bandit.k
    rewards = np.zeros(N)
    counts = np.zeros(k)
    values = np.zeros(k)

    for t in range(N):
        if t < k:
            # 最初のk回は、すべての腕を1回ずつ引く
            arm = t
        else:
            # UCBスコアを計算
            # countsが0にならないように微小値(1e-5)を加える
            ucb_values = values + np.sqrt(2 * np.log(t + 1) / (counts + 1e-5))
            arm = np.argmax(ucb_values)  # UCBスコアが最大の腕を選ぶ
        
        reward = bandit.pull(arm)
        counts[arm] += 1
        values[arm] += (reward - values[arm]) / counts[arm]
        rewards[t] = reward
        
    return rewards

確率一致法 (Probability matching method)

確率一致法は、UCBを進化させたアルゴリズムです。UCBでは、試行回数 t に対して、確率の判断にバイアスがかかっており、本来は期待値最大である可能性が小さい選択肢に対しても多くの探索を行ってしまいます。確率一致法は、それぞれの選択肢が期待値最大である確率を定式化し、選択肢をその確率で選んでしまう方法です。例えば、ソフトマックス法では、期待値最大である確率をソフトマックス関数で定式化します。

各腕の推定価値に基づいて、選択確率の分布を計算して腕を選びます。報酬が高い腕ほど選ばれやすくなりますが、報酬が低い腕も低い確率で選ばれる可能性があります。

P(a) = \frac{e^{Q(a)/\tau}}{\sum_{a=k}^{K} e^{Q(a)/\tau}}
  • Q(a): 選択肢 a の現在の推定報酬
  • \tau: 調整パラメータ

下記は、ソフトマックス法による確率一致法のコードです。

def softmax(bandit, tau, N):
    k = bandit.k
    rewards = np.zeros(N)
    counts = np.zeros(k)
    values = np.zeros(k)

    for t in range(N):
        # ソフトマックス確率を計算
        exp_values = np.exp(values / tau)
        probs = exp_values / np.sum(exp_values)
        
        # 計算された確率分布に従って選択肢を選ぶ
        arm = np.random.choice(k, p=probs)
        
        reward = bandit.pull(arm)
        counts[arm] += 1
        values[arm] += (reward - values[arm]) / counts[arm]
        rewards[t] = reward
        
    return rewards

事例：広告最適化におけるバンディット問題（A/Bテストの改善）

以下では、広告配信のA/Bテストを例に、バンディットアルゴリズムを比較してみましょう。

A/Bテストとは？

A/Bテストは、2つ以上の選択肢（例：AとB）を比較し、どちらがより良い成果を出すかを検証する方法です。マーケティングやWebサイト最適化の現場でよく使われます。例えば、あるWebサイトで「アグレッシブな広告（A）」と「落ち着いた広告（B）」のどちらがよりクリックされるかをテストする場合、ユーザーをランダムに2グループに分け、半数にA、残りにBを表示します。その後、どちらがより多くクリックされたかを比較します。

バンディットアルゴリズムによる最適化

このA/Bテストのシナリオは、各広告を選択肢（アーム）と見なすことで、バンディット問題を活用することができます。報酬は通常、クリック（1）か非クリック（0）のような二値的な結果が報酬となります。

実際に、Pythonコードを用いて、多腕バンディット問題 (Multi-Armed Bandit Problem)を３つのアルゴリズムで実施してみましょう。

  • 設定: 3本の腕（成功確率 0.2, 0.5, 0.8）を持つバンディットを用意し、1000回試行します。
  • 実行: 3つのアルゴリズムをそれぞれ実行し、各ステップで得られた報酬の系列を取得します。
  • プロット:
    • 横軸をステップ数（試行回数）、縦軸を「それまでの平均報酬」としてグラフを描画します。
    • これにより、どのアルゴリズムがより早く、より高い平均報酬に収束していくか（＝最適な腕を見つけ出して利用できているか）を視覚的に比較できます。
    • Optimal（灰色の破線）は、常に最も成功確率が高い腕（この場合は0.8）を引き続けた場合の理論上の最高性能を示しており、各アルゴリズムがどれだけこの理想に近づけるかを見るための基準となります。

コードの全体構成

  1. Bandit クラス: バンディットマシン（スロットマシン群）の環境を定義します。
  2. アルゴリズム関数(これまでの章で実装した関数):
    • epsilon_greedy: ε-Greedy法を実装します。
    • ucb: UCB (Upper Confidence Bound) 法を実装します。
    • softmax: 確率一致法（ソフトマックス法）を実装します。
  3. 実行とプロット: 上記のクラスと関数を使い、シミュレーションを実行して結果をグラフで可視化してみます。

ライブラリのインポート

import numpy as np
import matplotlib.pyplot as plt

Bandit クラス

バンディットマシンの環境をシミュレートするクラスを作成

class Bandit:
    """
    多腕バンディットマシンを表現するクラス
    """
    def __init__(self, true_probs):
        # true_probs (list): 各腕（アーム）の本当の成功確率のリスト
        self.k = len(true_probs)  # 腕の数
        self.true_probs = true_probs  # 各腕の成功確率（アルゴリズムからは見えない）
    
    def pull(self, arm):
        # 指定した腕を引くシミュレーションを行う。arm (int): 引く腕のインデックス
        # 指定された腕の成功確率に基づいて、報酬を返す
        return 1 if np.random.rand() < self.true_probs[arm] else 0

実行とプロット

シミュレーションを実行し、各アルゴリズムの性能を比較するためのグラフを描画します。

np.random.seed(42)  # 結果を再現可能にするための乱数シード

# 各腕の本当の成功確率を設定
true_probs = [0.2, 0.5, 0.8]
bandit = Bandit(true_probs)
N = 1000  # 全試行回数

# 各アルゴリズムを実行
rewards_eps = epsilon_greedy(bandit, epsilon=0.1, N=N)
rewards_ucb = ucb(bandit, N=N)
rewards_softmax = softmax(bandit, tau=0.1, N=N)

# 平均報酬の累積平均をプロット
plt.plot(np.cumsum(rewards_eps) / (np.arange(N) + 1), label='ε-Greedy')
plt.plot(np.cumsum(rewards_ucb) / (np.arange(N) + 1), label='UCB')
plt.plot(np.cumsum(rewards_softmax) / (np.arange(N) + 1), label='Softmax')

# 最適な腕を引き続けた場合の理論上の最大報酬
plt.axhline(max(true_probs), color='gray', linestyle='--', label='Optimal')
plt.xlabel('Steps')
plt.ylabel('Average Reward')
plt.ylim(0,1)
plt.title('Multi-Armed Bandit Comparison')
plt.legend()
plt.grid()
plt.show()

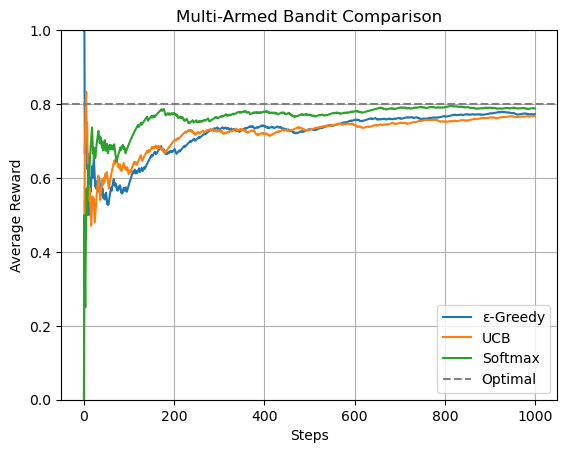
図表を見ると、確率一致法（Softmax）が序盤から良いリワードを獲得できていることがわかります。UCB法も高い性能を発揮していますが、初期の学習速度ではSoftmaxに劣る場面があります。一方、ε-Greedy法は序盤を中心に学習効率の面で課題があることが示されています。全体として、探索戦略の工夫が報酬の最大化に大きく影響を与えることが視覚的に確認できる結果となっています。

まとめ

多腕バンディットアルゴリズムが、限られた情報の中で、新しい選択肢を試す「探索」と、最も良いと分かっている選択肢を選ぶ「利用」のバランスを最適化することで、広告のA/Bテストのような最適化問題に対して活用可能であることを説明しました。

多腕バンディット問題は、複数の選択肢から繰り返し選びながら総報酬の最大化を目指す課題で、性能評価はリグレット（機会損失）によって行われます。理論上、どんなアルゴリズムでもリグレットの増加を対数オーダー（O(logT)）以下には抑えられないことが知られています。が、UCBアルゴリズムや確率一致法では、実現可能な理論限界と同じオーダーに到達可能であることから、今回のA/Bテストのような単純な問題に対して活用可能であることがわかります。

株式会社 STAR AI
株式会社 STAR AIPublication

株式会社 STAR AI（star-ai.jp/index.html）が運営するテックブログです！

Discussion