Zenn
SRE Holdings 株式会社Publicationへの投稿
🏅

ノーベル賞とAIと物理学と。（ホップフィールドネットワーク、ボルツマンマシン、イジングモデル）

ppmm
2024/11/20に公開
ニューラルネットワーク
ノーベル賞
イジングモデル
ホップフィールドネットワーク
ボルツマンマシン
tech

SREホールディングス株式会社のエンジニアの木津です。

さて、2024年のノーベル物理学賞は、米プリンストン大学のジョン・ホップフィールド氏とカナダのトロント大学のジェフリー・ヒントン氏への授与が発表されました。
授賞理由は「人工ニューラルネットワークで機械学習を可能にした基礎的発見と発明」。選考委員会は記者会見で「2人が貢献したAIの技術革新と発展は、他の物理学も大幅に進化させている」とも評価しています。

AIの基礎研究はたくさんありますが、今回は物理学賞ということもあり、本記事では、ニューラルネットワークに関する両氏の論文で提案された理論のアイデアと、物理理論とのアナロジーを取り上げてみたいと思います。ワクワクしますね☺️

本記事で取り上げる理論

本記事では以下のニューラルネットワーク理論(NN)を取り上げます。

  • ホップフィールドネットワーク
  • ボルツマンマシン

また、これらと関連する以下の物理理論(物理)を紹介します。

  • イジングモデル
  • 微視的状態の出現確率

イジングモデル（物理）

もともと強磁性体（磁石）をモデル化したもので、スピン系の代表的なモデルです。
1920年にドイツの物理学者ヴィルヘルム・レンツによって提案され、モデルの名前はレンツの博士課程の指導学生でありこの模型の研究を行っていたエルンスト・イジングにちなんでいます。

モデルのアイデア

  • 磁性体は格子点で構成される
  • i番目の格子点は、up(+1)かdown(-1)のどちらかの状態をとる(スピン変数s_i)
  • 系のエネルギーは、スピン間の相互エネルギーと外部磁場によるエネルギーとで表される

効果

このように磁性体のモデルを仮定して理論を発展させていくと、例えば以下のような結果が得られます。

  • 磁性体の相転移現象（高温になると磁石が磁力を失う）を説明でき、実験結果と一致する
  • 磁化の強さ（磁力）を定式化できる

ホップフィールドネットワーク（NN）

ホップフィールドネットワークはニューラルネットワークの一種で、ニューロン間に対称的な相互作用があるネットワークです。物理学のイジングモデルから着想を得ています。現在主流の機械学習モデルとは形が異なりますが、その原型となっています。
アメリカの物理学者であるジョン・ホップフィールドが1982年の論文で提唱したものが有名ですが、日本の数理工学者である甘利俊一も同じモデルを1972年に発表しており、Amari-Hopfield モデルとも呼ばれます。
ホップフィールドはこのモデルを用いて、脳神経の「連想記憶」を数理モデルで説明することに成功しています。

モデルのアイデア

  • 各ニューロンは全結合しており、ニューロン間の相互作用は対称
  • 各ニューロンは、マカロック・ピッツ型の入出力を持つ
  • 系のエネルギーは、ニューロン間の相互作用による項とバイアスによる項とで表される

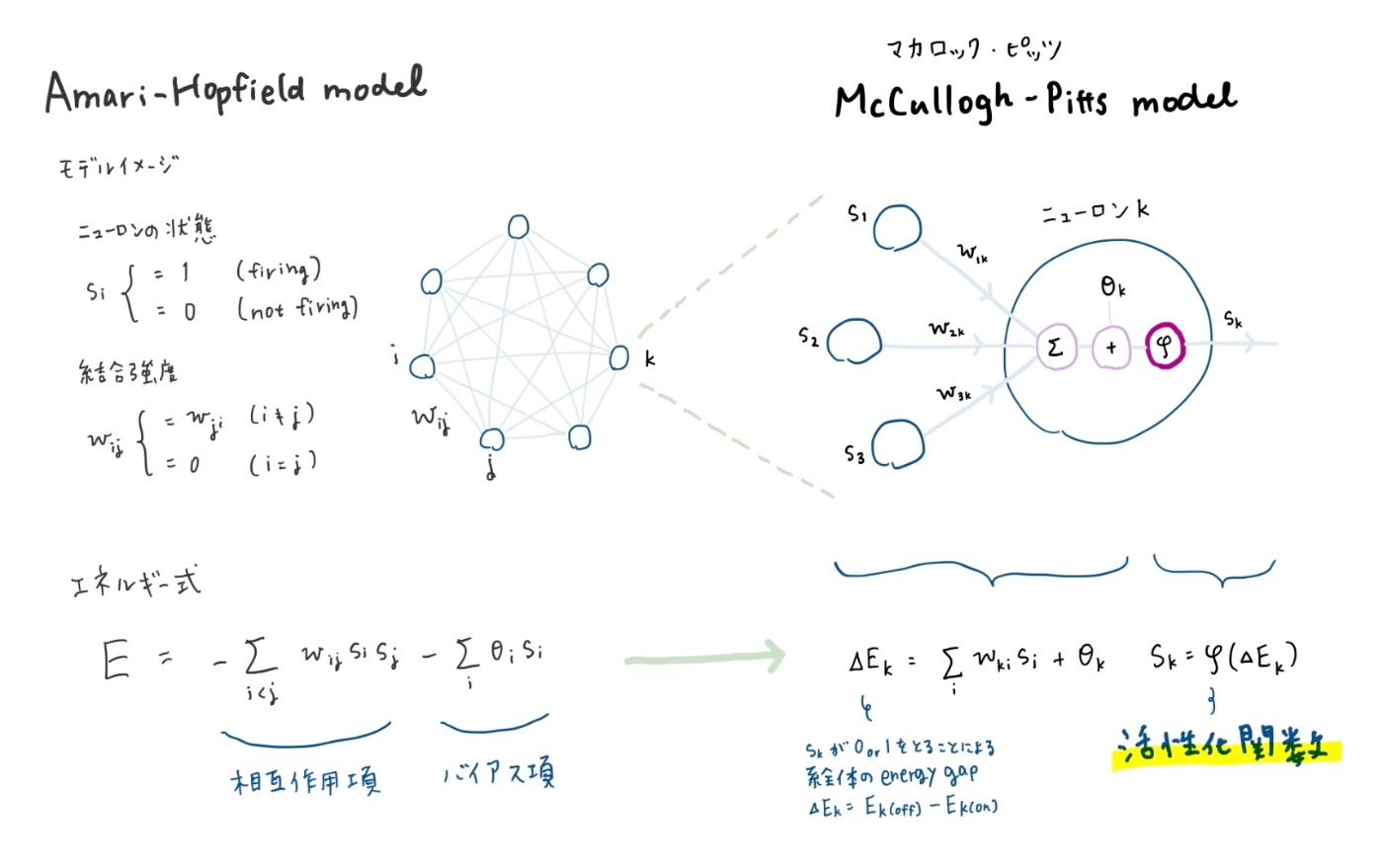
このように、エネルギーに注目して活性化関数φを逐次アルゴリズムとしてうまく設計することで、脳が働くようにモデルを動かすことができます。

連想記憶

ホップフィールドの論文では、部分的な記憶の断片から完全な記憶を思い出すという人間の脳の働きを「連想記憶」とし、ホップフィールドネットワークを用いて「思い出す」ことに数理的な解釈を与えています。

一般的な物理法則として、系はエネルギーが小さいほど安定します。系の状態は、時間とともにエネルギーが小さくなるように状態遷移し、エネルギーが極小となる平衡状態をむかえます。

この過程を、脳の記憶メカニズムの文脈では、以下のようにみなすことができます。

  • 完全な情報(aやbやc)は、エネルギーの極小点として記憶されている
  • 情報の部分的な知識(a+Δやb+Δやc+Δ)は、完全な情報にノイズが乗った形で表される
  • 系の自然な状態遷移により、システムは、情報に対する部分的な知識(a+Δ)から、完全な知識(a)を得る（連想記憶）

逐次アルゴリズム

情報に対する部分的な知識(a+Δ)から、完全な知識(a)を得る方法として、同論文では、以下の逐次アルゴリズムを提示しています。

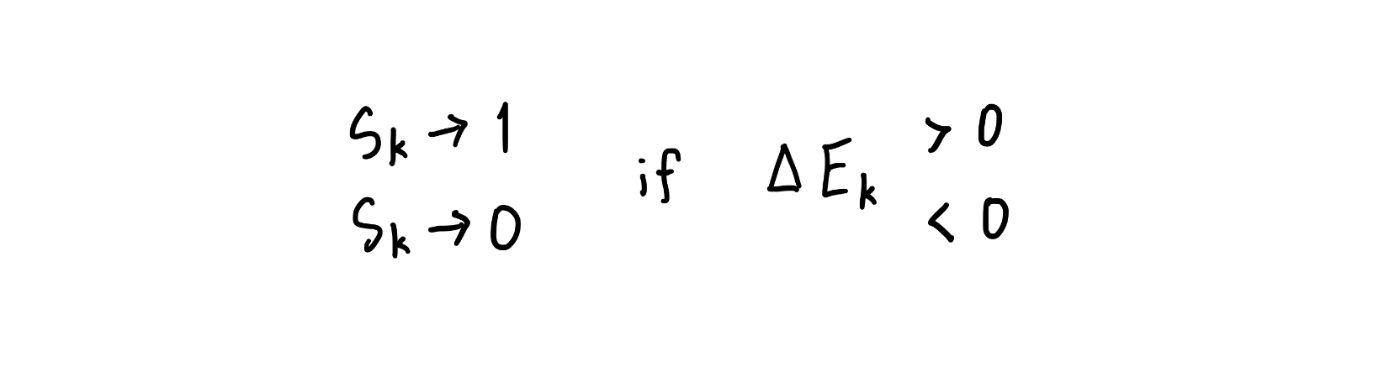
この逐次アルゴリズムにより、系のエネルギーが単調減少することが容易に示されます。

ボルツマンマシン（NN）

ジェフリー・ヒントンらは1985年に、ホップフィールドネットワークの発展形であるボルツマンマシンを発表しました。
モデルの構成は同じですが、最適化アルゴリズムとしてアニーリングの概念（ときどき高エネルギー状態にジャンプする）を取り入れることで、勾配法が局所解にとらわれてしまう問題に対処しており、適用可能な問題の幅を広げています。

ボルツマンマシンのメリット

ホップフィールドネットワークは、ニューラルネットワークとして情報を記憶、想起するのに使えました。その後このニューラルネットワークは、nクイーン問題やグラフ彩色問題などの組合せ最適化問題にも適用されるようになりました。このように全体最適解を探したい場合には、局所最適解にとらわれてしまうことが問題になってくるため、ボルツマンマシンのほうがより適したモデルとなります。

確率的な逐次アルゴリズム

ホップフィールドネットワークの逐次アルゴリズムは、入力から決定論的に出力を決めていました。
一方、ボルツマンマシンでは、次に示すような確率的な遷移によって出力が決まるようにアルゴリズムが構成されています。

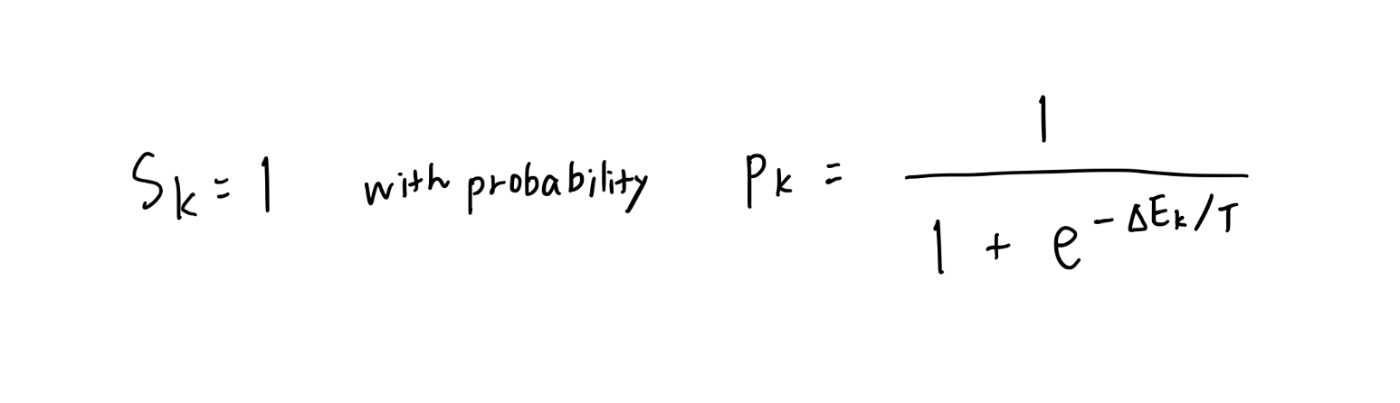
これは熱統計力学においてメトロポリスらが1953年に導入したアルゴリズムからきており、次に説明する微視的状態の出現確率を使って以下のように導出できます。

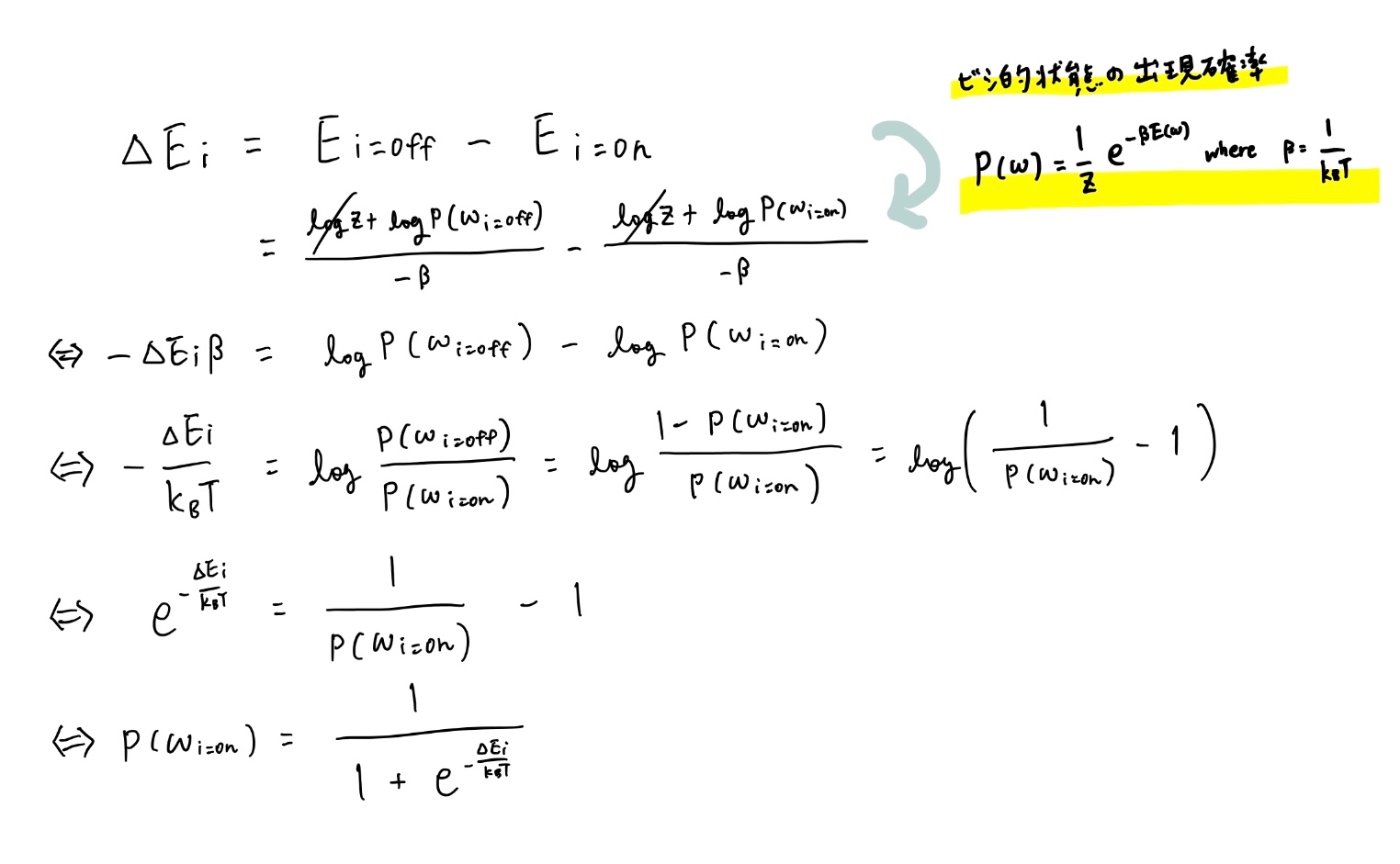
これは、各ニューロンが自然なゆらぎの中で、その時々のエネルギーに応じて次の状態をとることをモデル化したものと言えます。

微視的状態の出現確率（物理）

最後に、ボルツマンマシンの確率的な逐次アルゴリズムのもとになっている、熱統計力学における微視的状態の出現確率の導出をみてみます。

広い世界の中の、ある小さな系に注目して、「等確率の原理」というシンプルなアイデアから、注目する系と外の世界とのつながりを考えます。
全体が落ち着いた平衡状態にあるとき、注目している小さな系はどのようにふるまうのでしょうか。

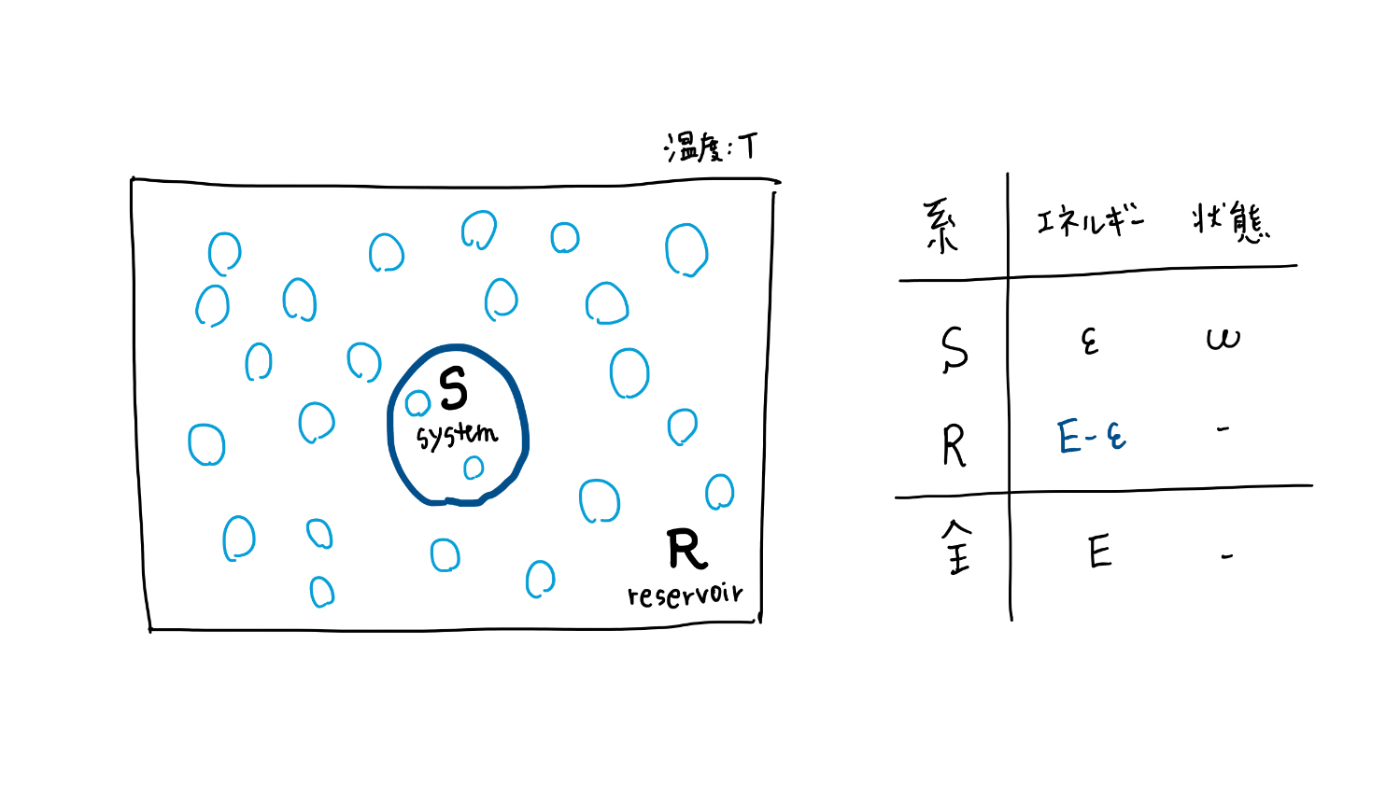
前提

  • 対象とする系S(system:システム)はミクロな系
  • 系Sは、それより非常に大きな系であるR(reservoir:熱浴)と接する
  • 系Sは、外部(系R)と熱のやりとりをする
  • 系Sと系Rを合わせた全系は、温度T、体積一定の独立系で、全体のエネルギーはE（一定）

これらの前提のもと、系Sが状態ωをとるときの、系Sのエネルギーをεとします。

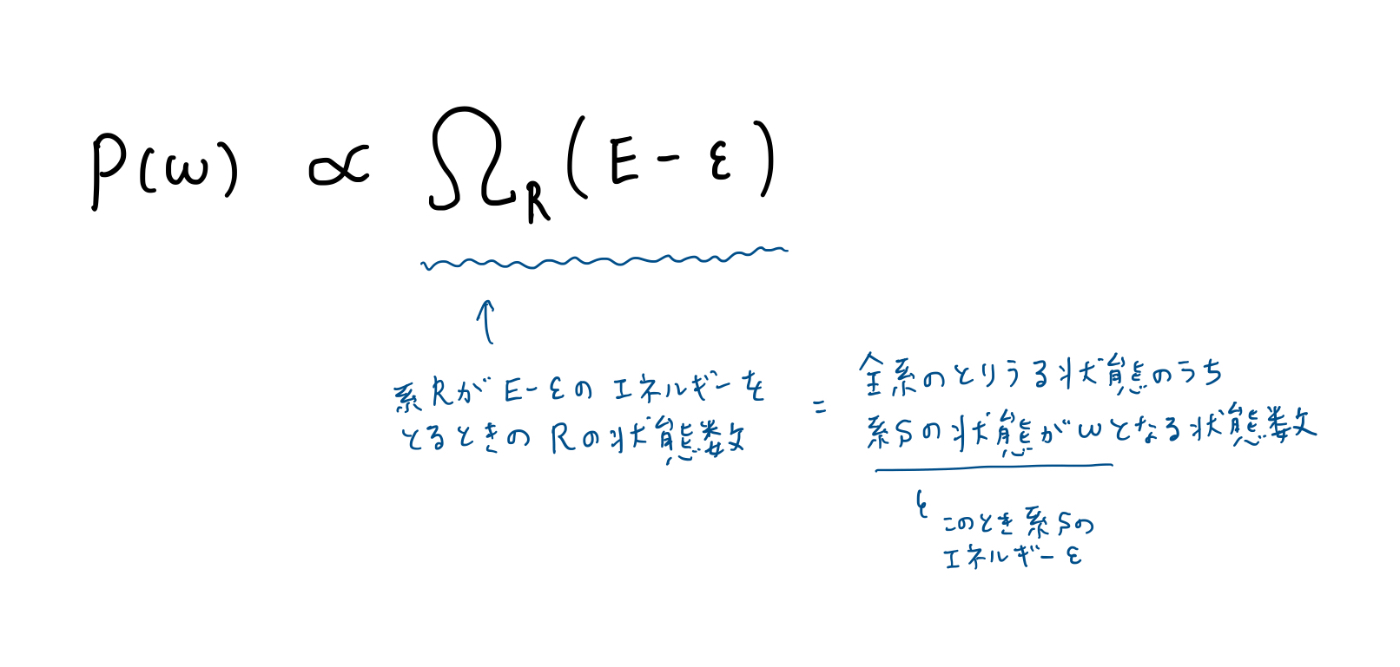
等確率の原理

統計力学では、「系の状態はどれも等しい確率で現れる」という等確率の原理を基礎としています。これにより、P(ω)は次のように表せます。

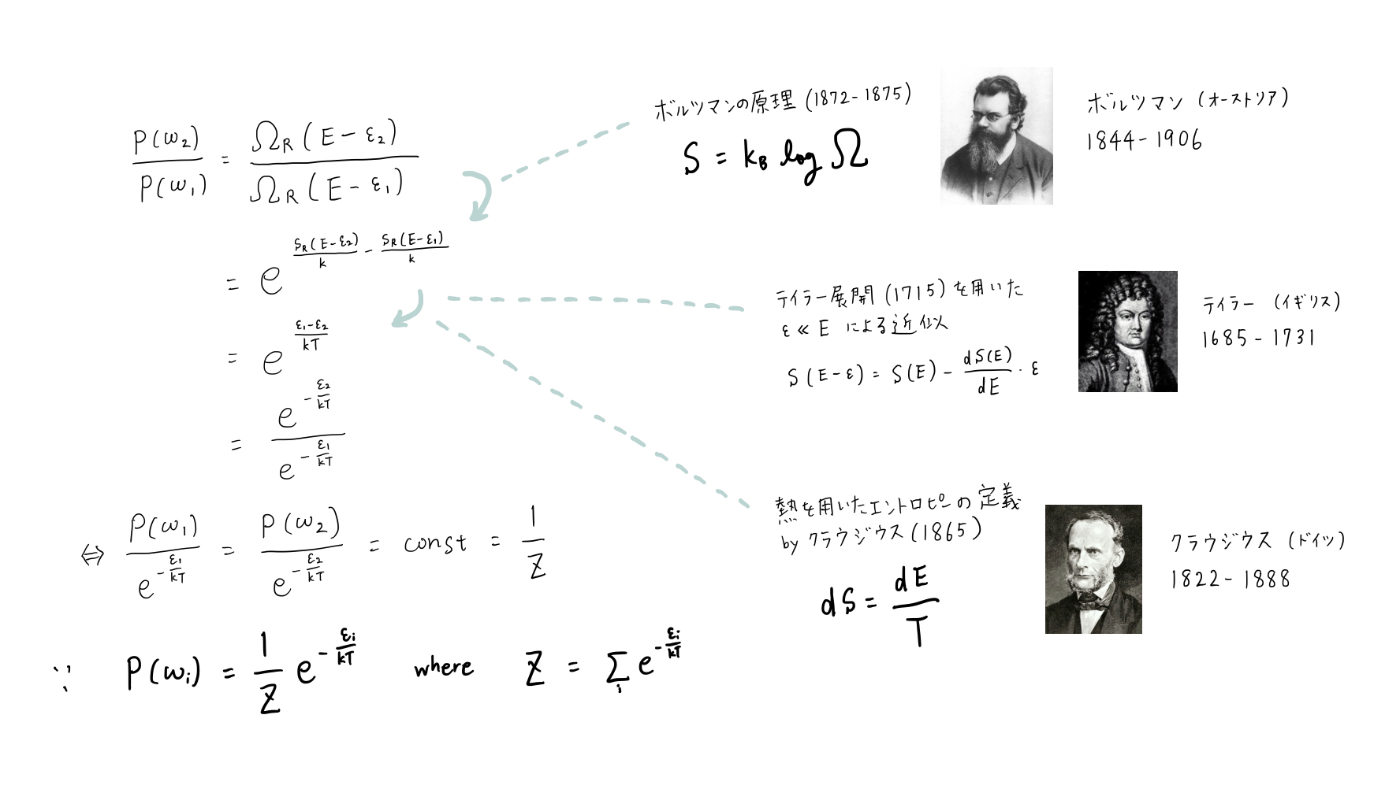
導出

系Sのふたつの状態の比を考えることで、以下のようにP(ω)を導出できます。

詳細解説はこちら

系Sの状態をω_i, その時のエネルギーをε_iとします（i = 1, 2, …）。ふたつの状態ω_1とω_2の出現確率を比べると、等確率の原理から、その比は系RがE-ε_1およびE-ε_2のエネルギーを取るときの状態数の比に等しいことが分かります。
一方、系Rは大きな（巨視的な）系であり、その性質を熱統計力学的な量（エントロピーS, 温度T等）で記述することが可能です。
具体的には、上記のように、状態数Ωをボルツマンの原理によりエントロピーSで記述し、i = 1, 2の乖離になる部分のみを近似しながら展開していきます。結果的に、定数倍を除いたP(ω_i)の形を導出できるため、この定数倍部分をZとおいてP(ω_i)を得ることができました。

ボルツマンマシンにおけるp_kは、1つのニューロンの状態に注目し、ニューロンが発火するかどうかの2状態をω_{on}, ω_{off}とした場合に上記の議論を当てはめると得られることが、容易に分かります。

おわりに

めくるめくNN物理ロマンの旅、いかがでしたか。物理学の考え方がAIの発展につながってきた歴史が感じられ、ワクワクしましたね☺️。
本記事では、ボルツマンマシンの状態を最適化するアルゴリズムのアイデアについてまでを説明しました。ここからさらに現在一般的な多層の深層NN（DNN, CNN等）の形になり、重みをどのように学習させていくか等、多くの発展を経て、今回のノーベル物理学賞の受賞にもつながっているのかと思います。
AIに限った話ではありませんが、たくさんの偉人が生み出してきた珠玉の結果の積み重ねが、今の進んだ世の中の基礎になっているのだと、執筆の過程でもあらためて実感しました。
最後に、NNの学習においても根幹となっている微分を発明したニュートンの言葉を借りて筆をおきたいと思います。

“If I have seen further, it is by standing on the shoulders of giants.” -- Isaac Newton

参考

SRE Holdings 株式会社
SRE Holdings 株式会社Publication

SRE Holdings株式会社の情報発信用ブログです

Discussion