凸包アルゴリズムでぐちゃぐちゃの図形をきれいな丸にする

はじめに

スペースマーケットでAndroidアプリの開発を担当しておりますseoと申します。

今回は、スペースマーケットのアプリv5.3.0以降に搭載された、地図上で丸を描いて検索する「囲んで検索」機能の実現方法について、簡単に紹介したいと思います！

本記事は、こちらの記事の続きになります。
前回は、GoogleMap上にフリーハンドで線を描く方法を解説しました。
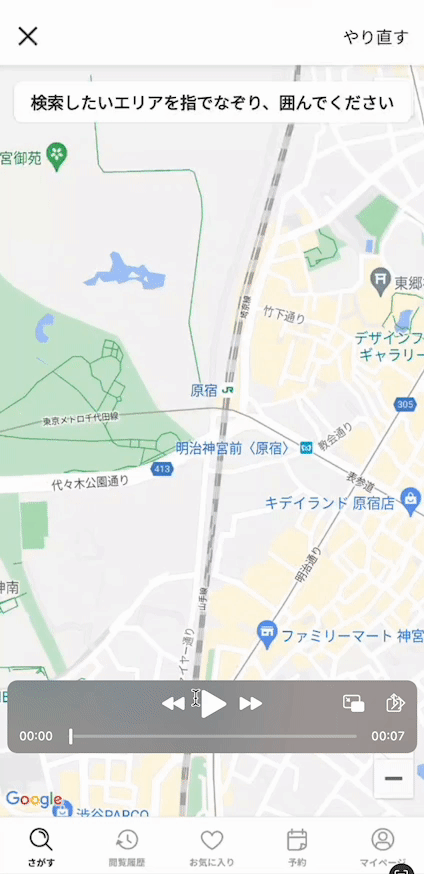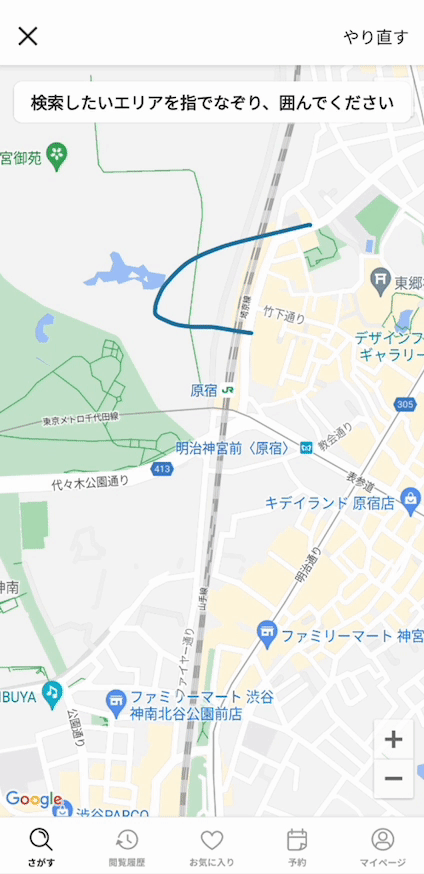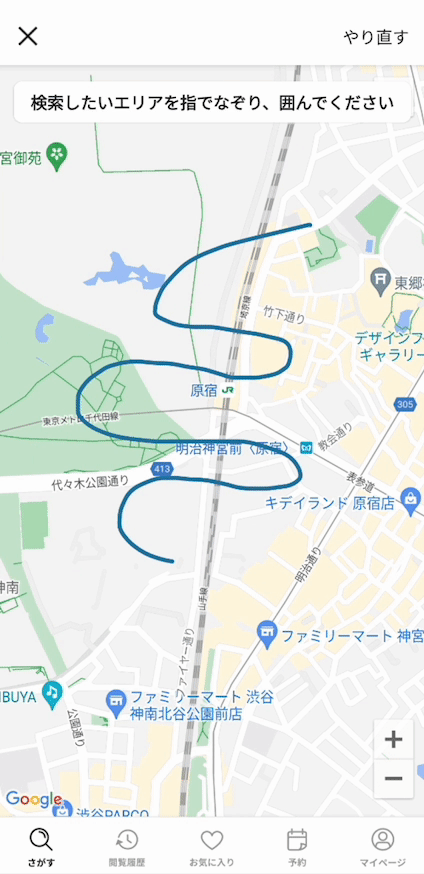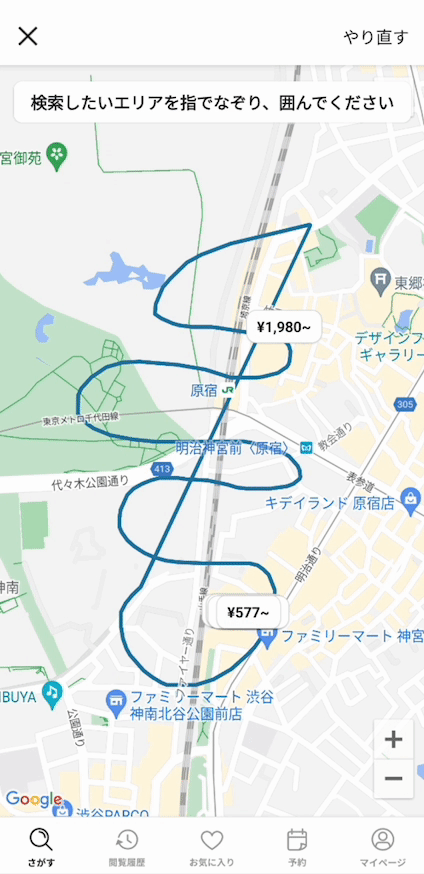
今回は、このような丸や円以外が描かれたときに、なめらかな丸に変換する方法を紹介します。

前回のおさらい

前記事で説明したとおり、なぞった軌跡をOffsetの配列でpositionsに格納していました。

var positions by remember { mutableStateOf<List<Offset>>(listOf()) }

val drawModifier = Modifier
    .pointerMotionEvents(
        onDown = { pointerInputChange: PointerInputChange ->
            positions = positions + listOf(pointerInputChange.position)
            motionEvent = MotionEvent.Down
            pointerInputChange.consume()
        },
        onMove = { pointerInputChange: PointerInputChange ->
	    // なぞった軌跡をpositionsに追加していく
            positions += listOf(pointerInputChange.position)
            motionEvent = MotionEvent.Move
            pointerInputChange.consume()
        },
        onUp = { pointerInputChange: PointerInputChange ->
            motionEvent = MotionEvent.Up
            pointerInputChange.consume()
        },
        delayAfterDownInMillis = 25L
    )

このpositionsの配列を凸包アルゴリズムを使って、交差のないOffsetの配列に組み替えるメソッドを作ります。

実装

先に最終的な完成のコードがこちらになります。

private fun makeConvexHullPointList(pointList: List<Offset>): List<Offset> {
    // 反時計回りにソート
    val sortedPointList = pointList.sortedWith { lPoint, rPoint ->
        if (lPoint.x == rPoint.x) {
            lPoint.y.compareTo(rPoint.y)
        } else {
            lPoint.x.compareTo(rPoint.x)
        }
    }

    val convexHullPointList = mutableListOf<Offset>()
    val MINIMUM_POLYGON_POINT_COUNT = 2

    // 左半分の凸包構築
    for (point in sortedPointList) {
        while (convexHullPointList.size >= 2 &&
            calculateCrossProduct(convexHullPointList[convexHullPointList.size - 2],
                convexHullPointList[convexHullPointList.size - 1], point) <= 0
        ) {
            convexHullPointList.removeAt(convexHullPointList.size - 1)
        }
        convexHullPointList.add(point)
    }

    // 右半分の凸包構築
    val upperHullSize = convexHullPointList.size + 1
    for (index in (0 until sortedPointList.size - 1).reversed()) {
        val point = sortedPointList[index]
        while (convexHullPointList.size >= upperHullSize &&
            calculateCrossProduct(convexHullPointList[convexHullPointList.size - 2],
                convexHullPointList[convexHullPointList.size - 1], point) <= 0
        ) {
            convexHullPointList.removeAt(convexHullPointList.size - 1)
        }
        convexHullPointList.add(point)
    }

    // 最後の重複を削除
    convexHullPointList.removeAt(convexHullPointList.size - 1)

    return if (convexHullPointList.size < MINIMUM_POLYGON_POINT_COUNT) {
        pointList
    } else {
        convexHullPointList
    }
}

private fun calculateCrossProduct(p: Offset, q: Offset, r: Offset): Float {
    val pq = Offset(q.x - p.x, q.y - p.y)
    val pr = Offset(r.x - p.x, r.y - p.y)
    return pq.x * pr.y - pq.y * pr.x
}

考え方としては、OffsetのListの中で、最も外側に存在する点を抽出して、凸多角形を構成しなします。

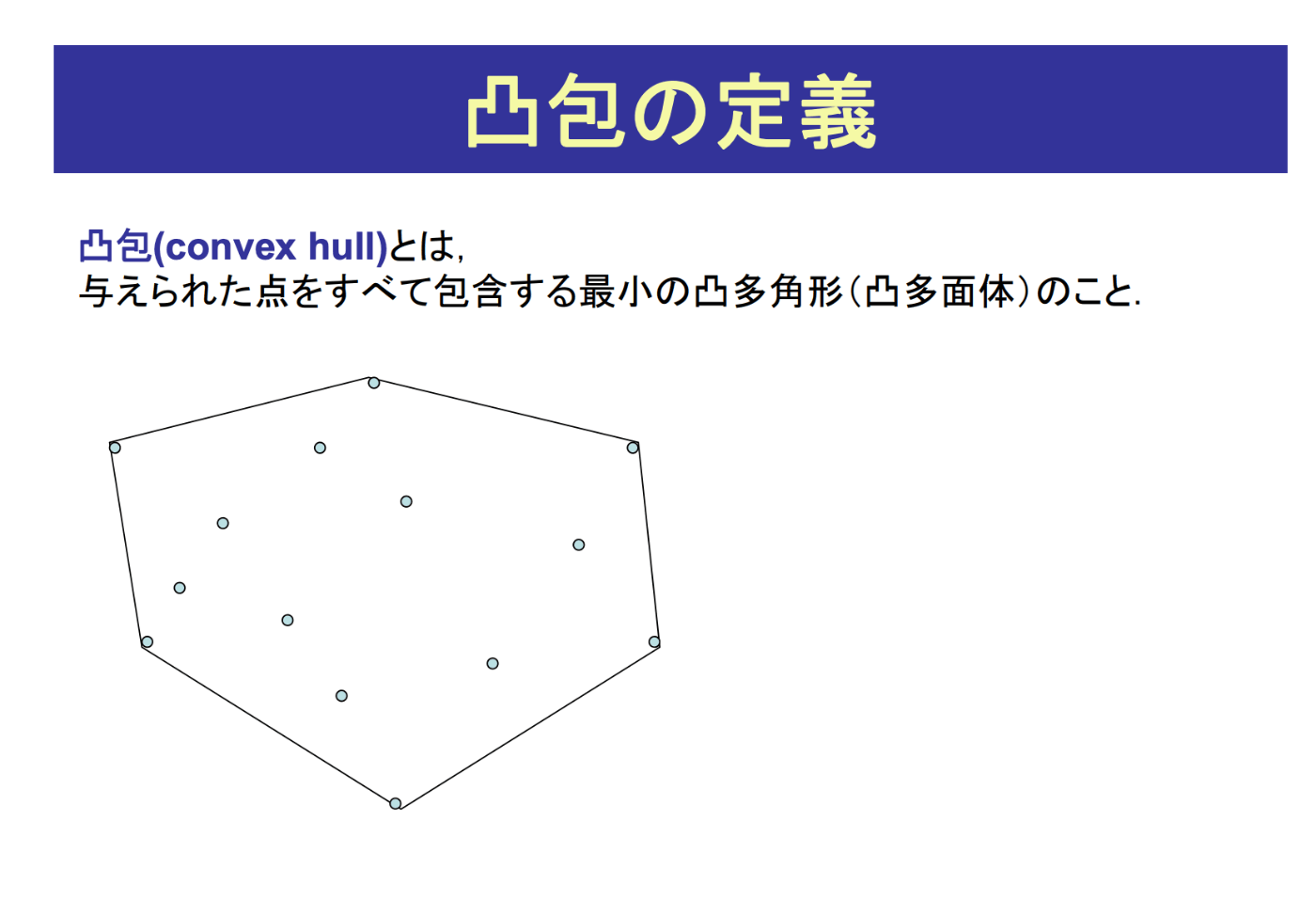
以下、メソッドの中身をひとつひとつ解説していきます。

1. 反時計回りにソート

val sortedPointList = pointList.sortedWith { lPoint, rPoint ->
    if (lPoint.x == rPoint.x) {
        lPoint.y.compareTo(rPoint.y)
    } else {
        lPoint.x.compareTo(rPoint.x)
    }
}

pointList内のをx座標を優先して昇順にソートし、x座標が同じ場合はy座標を使ってソートします。これにより、点が左から右にソートされ、sortedPointListに格納されます。

2. 変数

val convexHullPointList = mutableListOf<Offset>()
val MINIMUM_POLYGON_POINT_COUNT = 2

convexHullPointListは、後で凸包の頂点を格納するための可変リストです。
また、MINIMUM_POLYGON_POINT_COUNTは、凸包が少なくとも2つ以上の点から成る必要があることを示す定数です。

3. 左半分の凸包構築

for (point in sortedPointList) {
    while (convexHullPointList.size >= 2 &&
    calculateCrossProduct(convexHullPointList[convexHullPointList.size - 2],
	convexHullPointList[convexHullPointList.size - 1], point) <= 0
    ) {
        convexHullPointList.removeAt(convexHullPointList.size - 1)
    }
    convexHullPointList.add(point)
}

private fun calculateCrossProduct(p: Offset, q: Offset, r: Offset): Float {
    val pq = Offset(q.x - p.x, q.y - p.y)
    val pr = Offset(r.x - p.x, r.y - p.y)
    return pq.x * pr.y - pq.y * pr.x
}

• ここでは、反時計回りにソートされた点の中から、左半分の凸包を構築しています。
• 点 point が凸包に含まれるかどうかを判定するために、クロスプロダクト（calculateCrossProductメソッドを使用）を計算しています。クロスプロダクトが0以下の場合、点 point は凸包に含まれる可能性があるため、convexHullPointListに追加されます。

4. 右半分の凸包構築

val upperHullSize = convexHullPointList.size + 1
for (index in (0 until sortedPointList.size - 1).reversed()) {
    val point = sortedPointList[index]
    while (convexHullPointList.size >= upperHullSize &&
            calculateCrossProduct(convexHullPointList[convexHullPointList.size - 2],
        convexHullPointList[convexHullPointList.size - 1], point) <= 0
    ) {
        convexHullPointList.removeAt(convexHullPointList.size - 1)
    }
    convexHullPointList.add(point)
}

右半分の凸包を構築するために、sortedPointListの残りの点を逆順で処理しています。左半分の凸包と同様に、クロスプロダクトを計算して凸包に追加します。

5. 重複を削除

convexHullPointList.removeAt(convexHullPointList.size - 1)

return if (convexHullPointList.size < MINIMUM_POLYGON_POINT_COUNT) {
    pointList
} else {
    convexHullPointList
}

最後に、凸包の最後の重複を削除し、凸包の点の数が2未満の場合は元の点のリスト(pointList) を返し、それ以外の場合は凸包の点のリスト(convexHullPointList)を返します。

動作

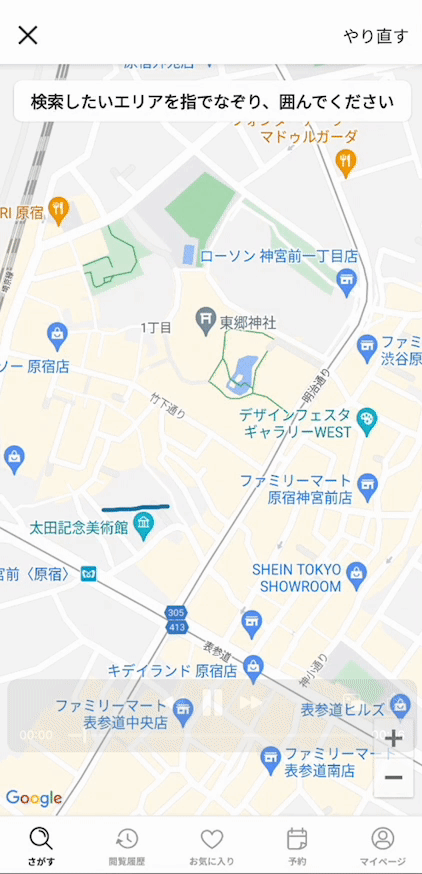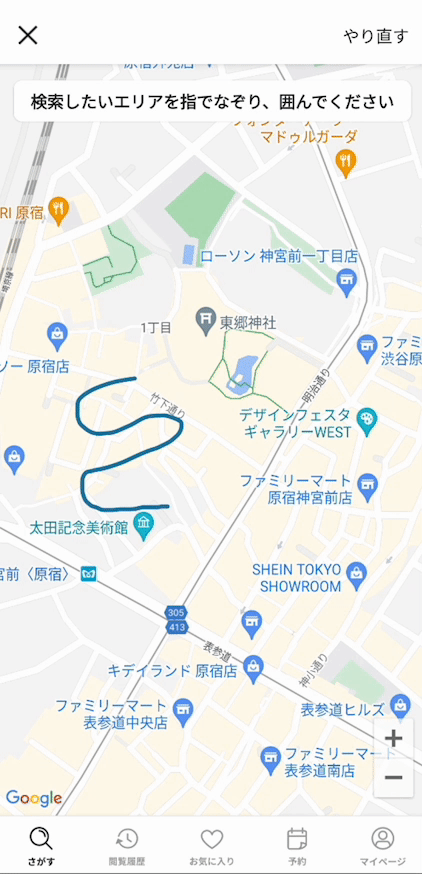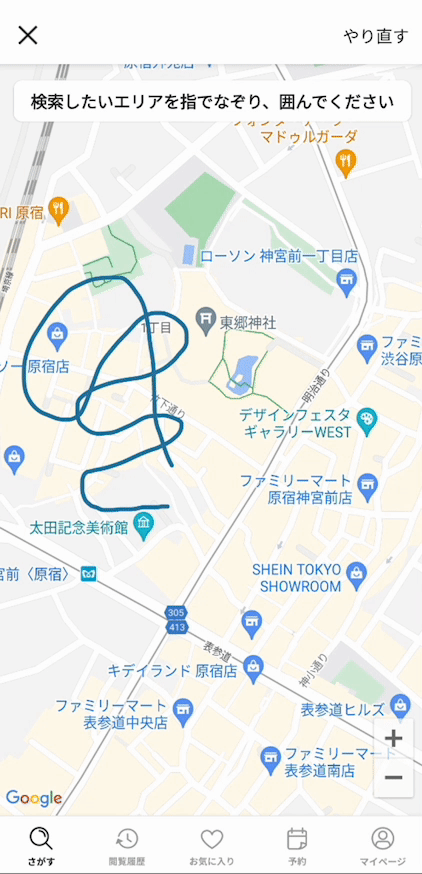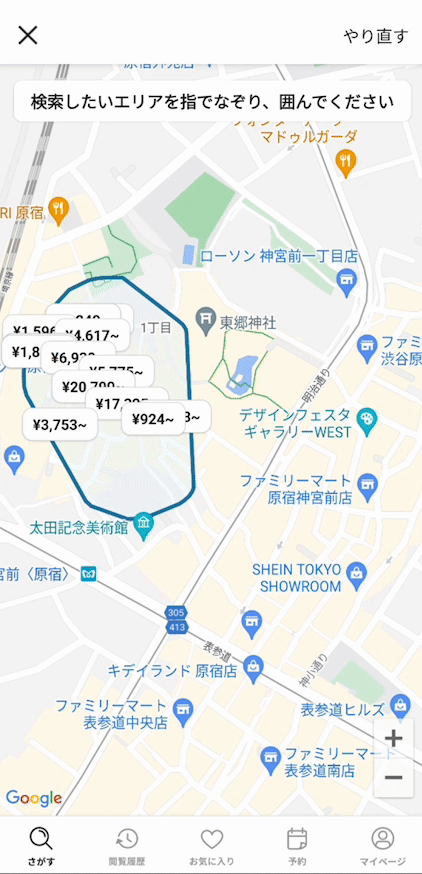
このような交差がたくさんあっても、描いた図形を含む丸に変換できるようになりました！

最後に

スペースマーケットでは一緒に働く仲間を募集しています！
カジュアルに話を聞きたいだけという方でも大歓迎ですので、ちょっとでも興味があれば以下からご応募お待ちしております！

▼SRE/インフラエンジニア
https://herp.careers/v1/spmhr/qZ-3RxrPtDgM

▼アプリエンジニア
https://herp.careers/v1/spmhr/m2LlDFRg7Ck0

▼フロントエンドエンジニア
https://herp.careers/v1/spmhr/oZ-mn0UYmzXj

▼エンジニア採用ページ（迷ったらこちらからどうぞ！）