多様体とは - 位相幾何学

目的

本投稿では位相幾何学の分野で説明される「多様体」の定義を明らかにし、実際にどのように応用されているのかを説明する。図形でイメージすることが難しい定義である場合も多いため、文章ベースで記述する。

多様体とは

現代の位相幾何学では、図形自身を独立した空間として扱う。例えば、球面$S^2$ (=2次元の球面)を図形ではなくそれ自体を独立した空間として扱う。「独立した$n$次元空間」を「$n$次元多様体」として定式化する。
ある空間$M$が$n$次元多様体であるとは以下(1)~(3)が成り立つことである。
(1) $M$のどんな点$p$について、$p$のまわりの$n$次元座標系が$M$の中に描けて、$p$の近くの点の位置はこの座標系で記述できる。(下図1) ただし、この座標系は空間$M$全体についても通用するとは限らない局所座標系である。定義(1)はM上のどんな点の周りにも$n$次元の局所座標系が存在するというもの、と解釈できる。

(2) 2つの局所座標系が重なり合う部分では、それらの座標系間の座標変換写像が何回でも微分可能である。下図2のように二つの局所座標系が重なり合う部分では、互いの座標系を重なり合う他の座標系の写像で書き表すことができる。
$y_1 = f_1(x_1,x_2,...,x_n)$
$y_n = f_n(x_1,x_2,...,x_n)$
この関数$f_1,...,f_n$が$x_i(i=1,...,n)$で何回でも微分可能であるという定義である。

(3) 空間$M$の中の相異なる任意の2点$p,q(p\neq q)$について、$p$の十分小さい局所座標系と$q$の十分小さい局所座標系とが互いに交わらないように取れる。(下図3)

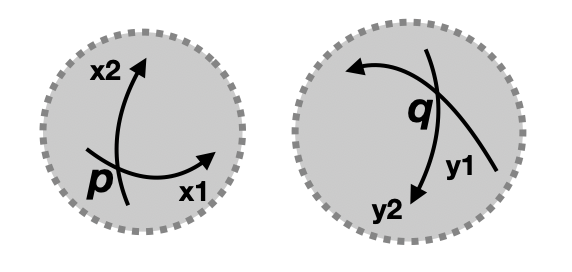
(1)~(3)を満たす簡単な多様体な例として、
・曲面は2次元多様体
・$S^n$($n$次元球面)は$n$次元多様体
また、多様体を組み合わせた直積と呼ばれる多様体も定義可能である。

$m$次元多様体$M^m$と$n$次元多様体$N^n$から、(m+n)次元の多様体(=直積)を作ることができる。この時、$M^m$の局所座標系と$N^n$の局所座標系をそれぞれ並べたものを、$M^m\times N^n$の局所座標系とする。

多様体は何に使われるか？

多様体は位相幾何学で登場している概念であるが、それだけでなく物理学や工学、情報科学の分野で応用されている。

分野	多様体の役割	具体的な応用例
物理学（相対論・場の理論）	時空や場を「リーマン多様体」「ファイバー束」としてモデル化	一般相対性理論（重力＝時空の曲がり）、ゲージ理論（素粒子の相互作用）
物理学（力学系・宇宙力学）	安定/不安定多様体で軌道の構造を記述	ラグランジュ点軌道設計、探査機の燃料効率の良い遷移軌道
工学（ロボット・制御）	姿勢や位置は「回転群 SO(3)」「配置空間」という多様体上の運動	ロボットの運動計画、ドローンや人工衛星の姿勢制御
工学（信号処理・通信）	高次元信号が低次元多様体上に分布すると仮定	次元削減による信号分類・異常検知、圧縮
データ科学・機械学習	高次元データの背後に潜む低次元構造を抽出	t-SNE, UMAP, Isomap などの次元削減、可視化
コンピュータグラフィックス	曲面や形状を多様体として扱う	3Dモデリング、滑らかなメッシュ生成、形状変形
医学・生体計測	データを多様体構造に埋め込むことで特徴を抽出	脳波・心電図の次元削減、医用画像解析
純粋数学	位相的・幾何的対象を統一的に扱う基礎概念	トポロジー分類、幾何学的構造解析、数理物理への応用