ベクトル制御
概要
永久磁石同期モータ(PMSM)を制御するための手法。
家電、ロボット、設備、ハイブリッド自動車、電気自動車に広く使われるため、弊社のエンジニアの必須知識と言える。
誘導機もベクトル制御だが、アラゴの円盤の原理でトルクを発生させるため、滑りに関する処理が追加される。本記事では省略する。
永久磁石同期モータ(PMSM)
利点
- トルク制御可能
- 小型高出力
- 高効率
- 動作範囲大
- 始動が滑らか
- 回生エネルギーの活用可能
欠点
- 制御が大変
- 適合が面倒
- 高回転の効率が悪い
適用先
- EV、HEV、産業用ロボット、サーボモータ、エアコン、洗濯機
力行と回生
- 力行:モータの回転方向に発揮するトルク
- 回生:モータの回転方向と逆向きに発揮するトルク
回路概要
以下のような上下アームからなる回路で構成される。
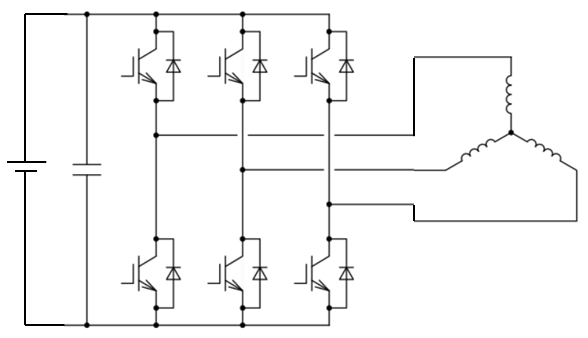
基本的な概念
制御ブロック図
速度制御のブロック図を以下に示す。
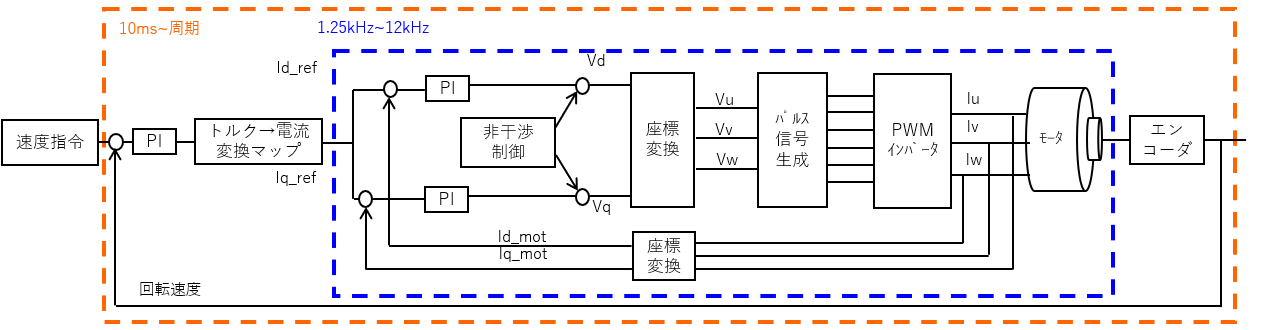
以下の順番で制御を実施する。
- 上位システムから速度指令(or トルク)を受け取る
- 現在の速度と指令速度の差分をPI制御器に入力し、指令トルクを取得
- 取得したトルクをdq電流指令に変換する
- dq軸電流の指令と現在値の差分をPI制御器に入力し、指令電圧を取得
- 誘起電圧の項をフィードフォワードで加える
- 取得した指令電圧を三相に変換
- デッドタイム追加と補償を行い、UVWの上下アームにONOFF指令
- モータに電圧が印加され、電流が流れる
- 取得した電流をdq変換し、二相に変換する
- エンコーダ(レゾルバ)で取得した値を速度に変換する
回転磁界
PMSMは回転するロータと止まっているステータから構成される。
ロータは磁石であり、N極とS極がある。
ステータはコイルからなり、コイルに電流を流すことにより磁界が発生する。
この磁界は磁石の向きと直行方向に発生させる必要があり、磁石が回転するため「回転磁界」と呼ばれる。
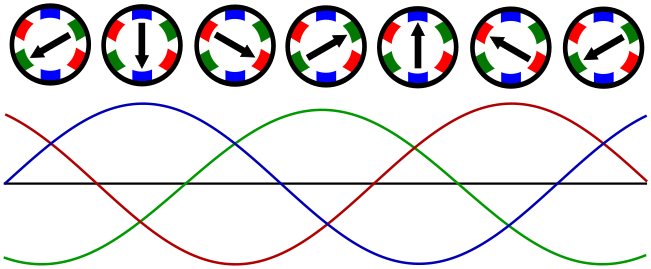
模式図(gifが動かないので、wikipediaを参照すること。)

ベクトル制御の必要性
ベクトル制御の目的は回転磁界を作ることである。
単純に考えると、
- 三相の電圧を印加
- 三相の電流が流れる
- 回転磁界が発生する
を行えば、モータトルクを発揮できる。
この方法に対してベクトル制御は以下の利点がある。
- 高効率な駆動が可能
- トルクの制御が可能
ここから上記が可能な理由を説明する。
PMSMの特性
SPMSM:表面磁石
- 磁石を表面に張り付けたモータ
- 磁石飛散防止のための部品が必要
- 振動が小さい
- リラクタンストルクを活用できない
- 制御が簡単
- 適用先:コンプレッサ
IPMSM:埋込磁石
- 磁石を内部に埋め込んだモータ
- 磁石を埋め込むので量産効果が高い
- 振動が大きい
- リラクタンストルクを活用できる
- 制御が難しい
- 適用先:HV、EV

PMSMが発揮するトルク
PMSMのトルクは以下の二つの合成トルクである。
- マグネットトルク:回転磁界の極と回転子の永久磁石の磁極との吸引及び反発によって発生するトルク
- リラクタンストルク:固定子の回転磁界による極と回転子の突極との吸引力だけによって発生するトルク
リラクタンストルクの簡易的な説明が以下である。

リラクタンストルクの詳細な説明
以下にマグネットトルクとリラクタンストルクの合成トルクの図を示す。
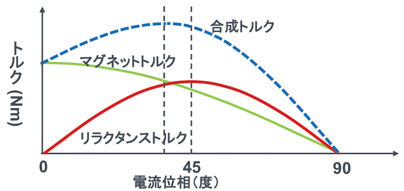
上図の電流位相は電流進角と呼ばれ、0°を磁石の直行方向と定義する。
つまり、上図はx軸の0°が磁石の直行方向。90°が磁石の方向である。
上図のように合成トルクが最大になるのは、電流進角が0~45°の間である。
合成トルクが最大になるように、電流進角を制御する必要がある。
dq変換
導入
PMSMでトルクを発揮するためには電流進角を制御する必要があることを説明した。
ここからどのように電流進角を制御する手法を説明する。
αβ変換(クラーク変換)
Iu + Iv + Iw = 0 であるため、1変数を減らすことができる。
3相の電流を(Iu、Iv、Iw)、2相変換後の電流を(Iα、Iβ)とすると、以下の式が成り立つ。
Iu + Iv + Iw = 0
Iα= Iu
Iβ= (Iu + 2Iv) / sqrt(3)
上式を行った結果が以下である。
三相の電流(Iu、Iv、Iw)を、「U相電流と同じ電流とU相から90°傾いた電流」 である二相の電流(Iα、Iβ)に置き換えることができた。

dq変換(パーク変換)
二相の電流(Iα、Iβ)はsin波である。
(Iα、Iβ)はローターを流れる電流値であり、ローターと一緒に回転している。
外から見れば、二相の電流(Iα、Iβ)はsin波であるが、ローターから見れば2相電流は止まって見える。
上記を表したのが下図である。
モータが回転するのに応じてαβ電流も回転するが、dq電流はモータの回転に合わせて回転する。
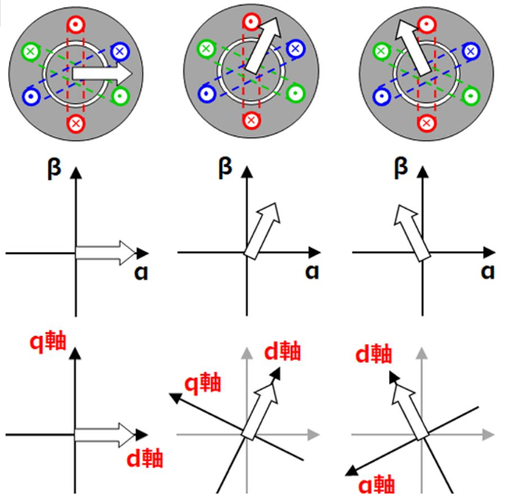
これを数式で行うのがdq変換である。
dq変換を次式に示す。回転行列を(Iα、Iβ)に乗ずるだけである。
Id = Iα・cosθ+ Iβ・sinθ
Iq = -Iα・sinθ+ Iβ・cosθ
まとめ
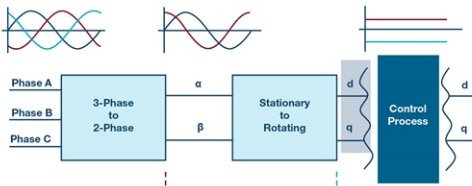
(Iu、Iv、Iw)➡(Iα、Iβ)➡(Id、Iq)を図示したのが以下である。
三相の交流電流が二相の直流電流に変換されたことが分かる。
電圧方程式
ここまでにdq軸電流の計算方法を説明した。
次にdq軸電圧のVdVqの計算方法を説明する。
VdVqは以下の電圧方程式で表せる。

(モータ制御の仕事をしている人で電圧方程式を覚えてない人はポンコツ間違いなし。)
電圧方程式の導出方法を説明する。
まず、キルヒホッフの法則より、電流から発生する電圧は、
(Ra + pLd)Id
(Ra + pLq)Iq
p:時間微分演算子
次にインダクタンスから発生する磁界は、
Φd=LdId
Φq=LqIq
このインダクタンスから発生する磁界は下図のように回転する。
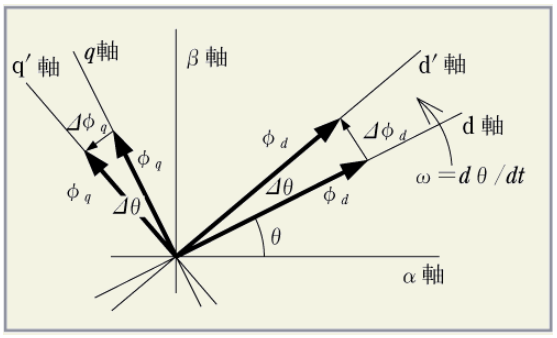
ファラデーの法則から磁束の時間変化|dΦ/dt|=wΦとなり、インダクタンスから発生する電圧は、
wLdId
-wLqIq
磁石から発生する電圧も同様に導ける。
wψa
ここまで導いた式をまとめると次式が導かれる。
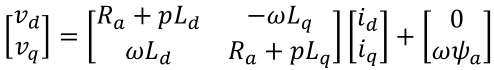
トルクの式
先に説明したようにPMSMのトルクは、マグネットトルクとリラクタンストルクから成る。
- マグネットトルク:回転磁界の極と回転子の永久磁石の磁極との吸引及び反発によって発生するトルク
- リラクタンストルク:固定子の回転磁界による極と回転子の突極との吸引力だけによって生ずるトルク
上記を示したのが次式である。
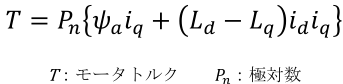
右辺第一項がマグネットトルク、右辺第二項がリラクタンストルクである。
IdIq電流の他はモータ定数であり、トルクを制御するためにはIdIq電流を制御すれば良いことが判る。
実現手法
NTカーブ
回転数NとトルクTを示すカーブである。
横軸に回転数、縦軸にトルクを取る。(逆にTNカーブと表す人もいる。)
回転数ごとに、発揮できるトルクを示す。
下図の場合、1800rpmまでは10Nmまで回せるが、
それ以上は回転数が上がるに連れ、発揮するトルクが下がる。
その境界を「基底の肩」と呼ぶ。
(基底の肩までのトルク上限は電流で決まり、基底の肩以降は電力で決まる。)
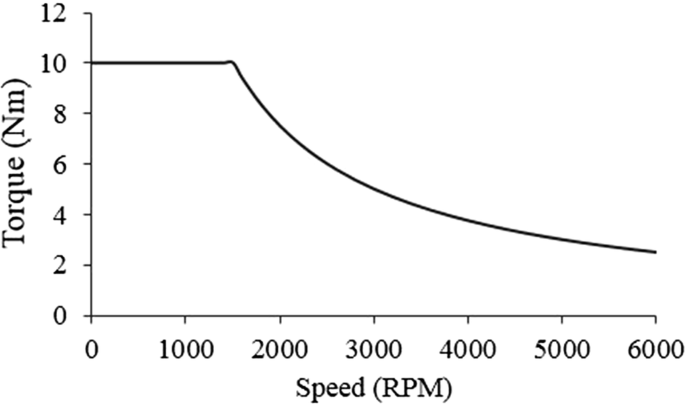
ここからはPMSMを如何に省電力かつ広範囲に駆動するための技術を紹介する。
トルク→電流変換マップ
トルクからIdIq電流を決定する。
電力が足りている範囲と足りていない範囲で決め方が異なる。
- 最適電流制御:電力が足りている範囲
- 弱め磁束制御:電力が立ちていない範囲
図で表すと以下である。
回転数が大きくなると電圧が足りなくなり、磁束を弱める必要がある。
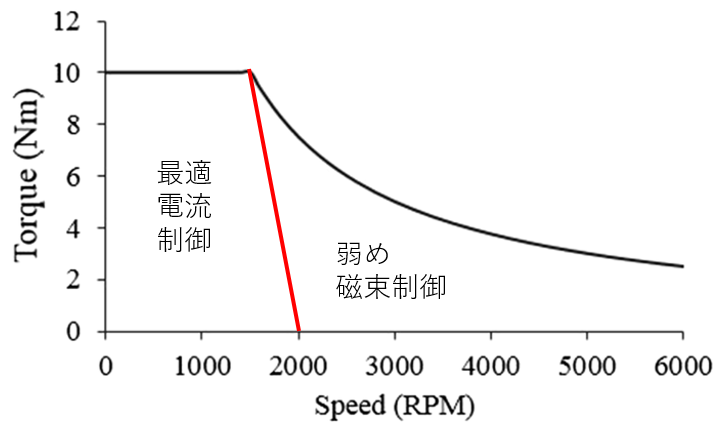
以下の議論は全て数式から導かれる値を用いる。
(実際のモータはインダクタンスの重畳特性やdq軸間磁束干渉により理論計算値とはズレる。)
最適電流制御(MTPA)
「埋込磁石同期モータの設計と制御」のP18のIPMSMのモータ定数を用いて、最適電流制御の例を示す。
極対数:2
永久磁石による鎖交磁束:0.1Wb
d軸インダクタンス:9.0mH
q軸インダクタンス:22.5mH
電機子巻き線抵抗:0.5Ω
このモータ定数を用いて、電流進角によるトルクをプロットしたのが下図。
電流進角を10°ごとしかプロットしていないため、確かではないが、電流進角が40°の時に最も大きなトルクを発揮する。

常に電流進角40°で動作させると、急激にId電流を流す必要があるため、実用上は以下のように零から滑らかに繋ぐ。
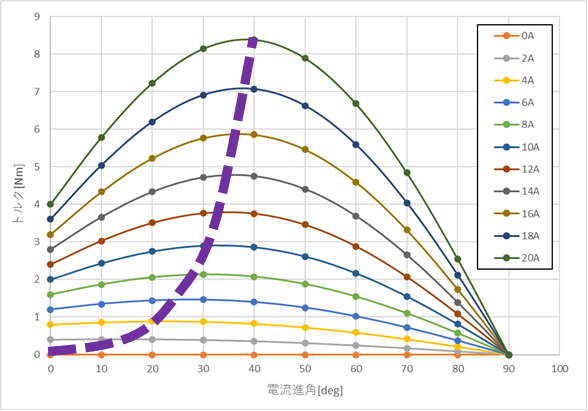
低電流時には電流進角が小さくても、発揮トルクはほとんど変わらないため、問題とならない。
上図の繋いだ線とトルクの関係から、トルク➡電流進角➡IdIqマップを生成することができる。
これが最適電流制御である。
最適電流制御の時の電圧を電圧方程式から導き、出力電圧を示したのが以下。
(計算が面倒だったので、電流進角を40°に固定した。)
48V x 0.78以上を赤く塗っている。この範囲では、電圧が足りず目的のトルクを発揮できない。
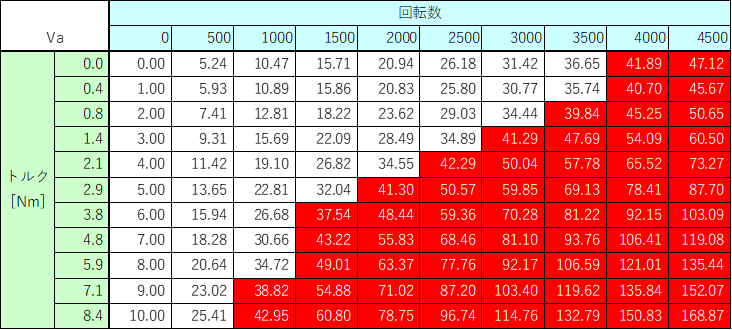
弱め磁束制御
最適電流制御では動作できない範囲を制御する方法が弱め磁束制御である。
以下のベクトル図を見れば分かるように、d軸電流Idを流すことで、磁石による磁束を弱めることができる。
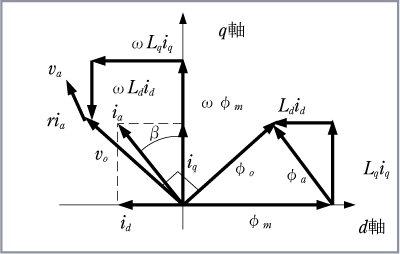
弱め磁束制御はd軸(磁石方向)に電流を流し、磁束を弱める制御を弱め磁束制御と呼ぶ。
最適電流制御の電流進角からd軸方向に倒して、出力電圧を弱めることによって出力範囲を拡大する。
Excel VBAで簡易的に計算した電流進角を以下に示す。電圧が足りない領域において電流進角が倒れていることが判る。
(電流進角を線形で倒すように細工している。)
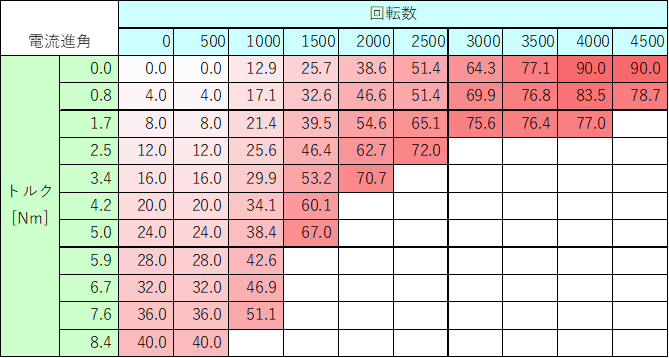
拡大された範囲が以下である。
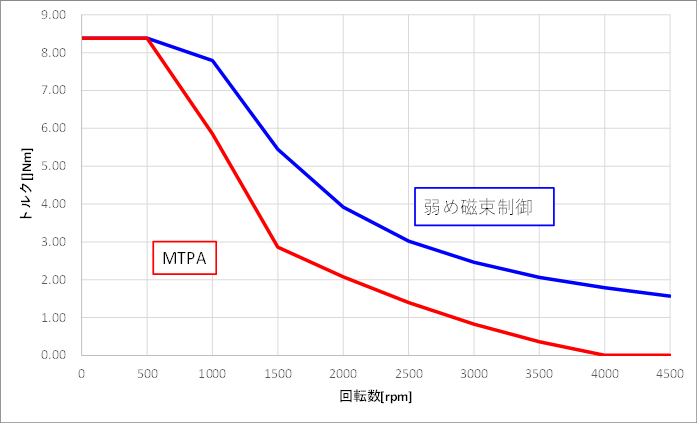
MTPAでの動作可能範囲から大幅に拡大したことが判る。
実用上、役に立つかは分からないが数式によりId電流を決定する方法がある。
私は使ったことがないので有用性は分からない。
数式を見ると、Iqを決定するためにIdやIaを用いる。通常は、トルクからIdIqを求めるので、使いにくいように感じる。

引用サイト
ベクトル制御
ここまでに指令IdIqを決定する方法を説明した。
ここからは指令IdIqに実IdIqを追従させる方法を説明する。
重要な点は、電流ベクトルIdqになるように、電圧ベクトルVdqを決定することである。
(電流ベクトルを電圧ベクトルで制御するので、ベクトル制御と呼ばれている。)
それを詳細に示したのが下図である。
モータに流したい電流ベクトルに対して、どのような電圧ベクトルを印加すれば良いかが説明されている。
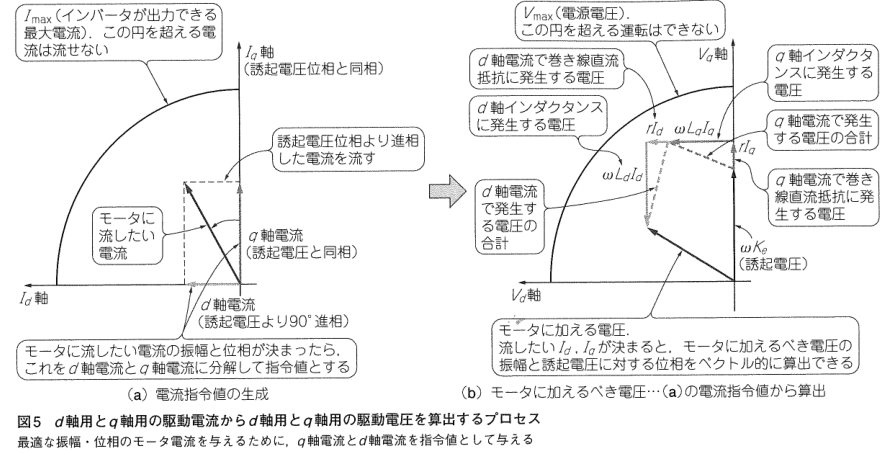
ベクトル制御では、非干渉制御とPI制御の二つの制御により電圧ベクトルを生成する。
もう一度、電圧方程式を確認する。
青枠で囲んだ電圧を非干渉制御で決定し、囲んでいない電圧をPI制御で決定する。
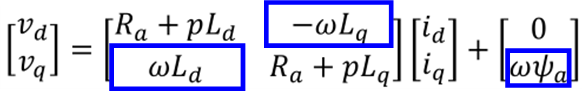
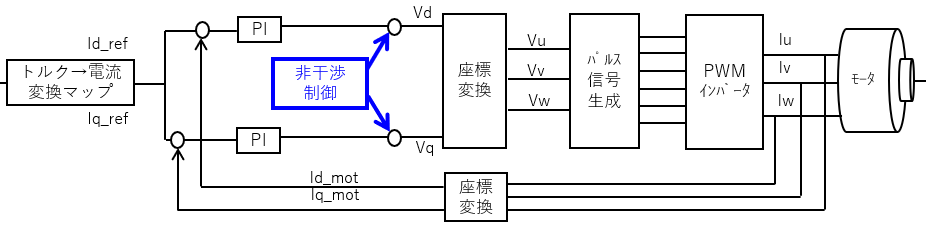
非干渉制御
誘起電圧に関する項をフィードフォワードで印加する手法である。
この制御を行うことで、制御対象を線形化でき、電流の応答性を向上することができる。
非干渉制御はブロック図の青枠にFF項として設ける。
以下のように非干渉制御項VdVqを計算する。
Vd = -ωLqIq
Vq = wLdId + ωψ
上式のIdIqには、以下の選択肢がある。
- モータの実電流
- モータの実電流のフィルタ値
- モータの指令電流のフィルタ値
- モータの指令電流
実電流は数値が安定せず、指令電流はまだその誘起電圧が発生せず不安定になる欠点がある。
実用上は指令電流のフィルタ値くらいが丁度良い気がする。(主観)
PI制御
非干渉制御で線形化された制御対象をPI制御で制御する。
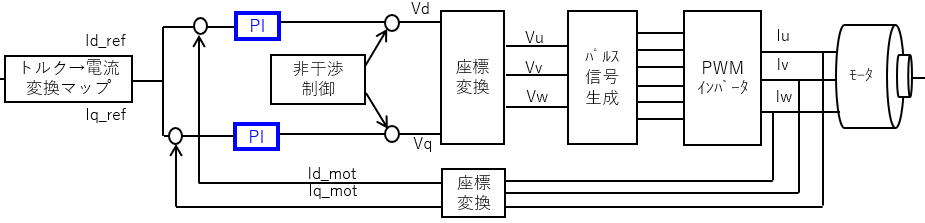
PI制御は、微分項がないPID制御器であるため、説明は以下の記事を参照すること。
PID制御とは
変調
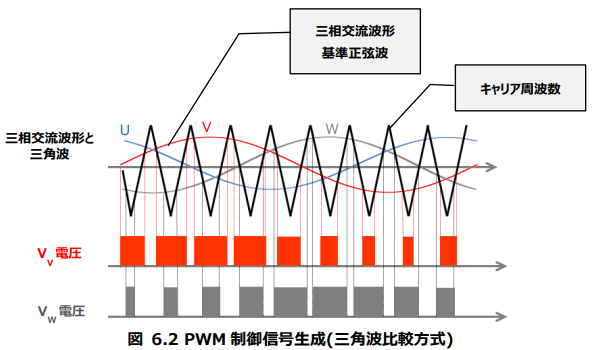
PWM制御(キャリア、三角波比較方式)
モータに印加する電圧を調整するためには、パルス幅を調整するPWM方式が広く使われる。
(ルームエアコンや冷蔵庫、洗濯機といった家電品のモータの回転数制御に、PAM方式のインバータが使われる。)
PWM制御では、キャリアと呼ばれる三角波と正弦波を比較することによって、パルス波を生成する。
キャリアの周波数をキャリア周波数と呼ぶ。
実現方法(詳細)
- PWM(Pulse Width Modulation)とは、半導体を使った電力を制御する方式の1つ。
- オンとオフの繰り返しスイッチングを行い、出力される電力を制御する。
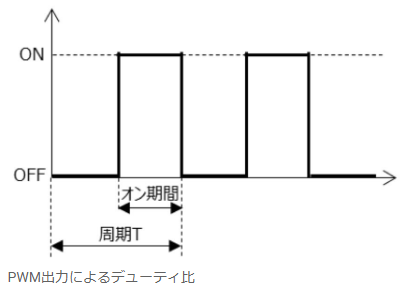
- 半導体のスイッチング信号をPWM信号で指示することで、平均電圧(Vout)を制御する。

- 実用上は以下のように変調波と比較することでパルス波を生成する。

- 実際にモータに印加されるのは線間電圧であることに注意すること。(特殊なオシロスコープが必要)

変調率
変調率の定義には3つの派閥がある。
- 直流電圧に対しての出力線間電圧実効値を変調率と定義する派閥
- 三次高調波重畳方式(二相変調)の最大電圧出力時を変調率1と定義する派閥
- 三角波比較PWM方式の最大電圧出力時を変調率1と定義する派閥
変調率の会話をする際には、「二相変調のMaxを1とする変調率では、矩形波制御の変調率は1.1まで使える。」
みたいな面倒くさい言い回しをする必要があるので注意。
私は2の派閥だが、手元の資料が1だったので以下は1で説明する。
以下に変調方式による動作範囲を示す。変調方式により動作範囲が異なることが分かる。

三相変調
- 最も簡単かつ有用な手法。
- 変調率が二相変調に劣るが、3次高調波重畳を用いることで同じ変調率まで利用できる。
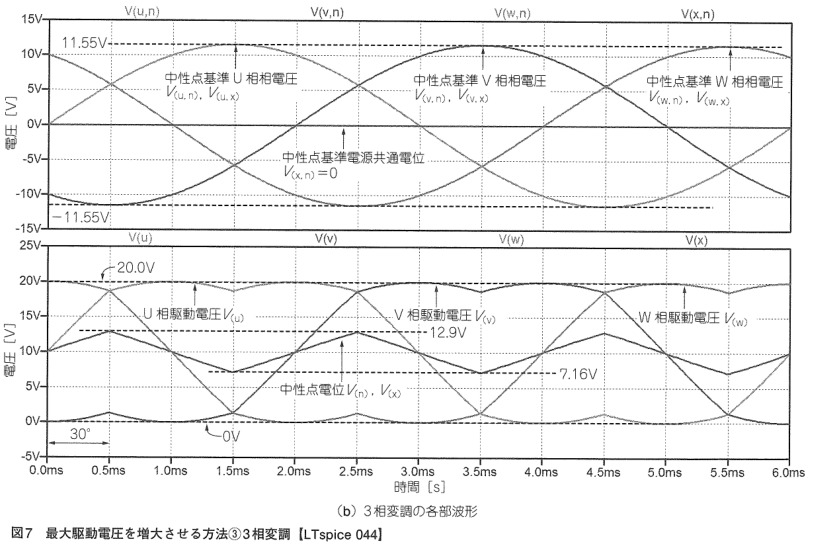
以下に三相変調のキャリアと変調波。その比較によって生成されるVu, Vv, Vw。
実際にモータに印加されるVu-v, Vv-w, Vw-uを示す。

二相変調
三相変調に対して、スイッチング方法に工夫を加えたのが二相変調である。
三相変調波のうち電圧指令値が最低値となる一相の下アームパワー素子をその期間(120°)オンに固定し、
他の二相を変調させる。
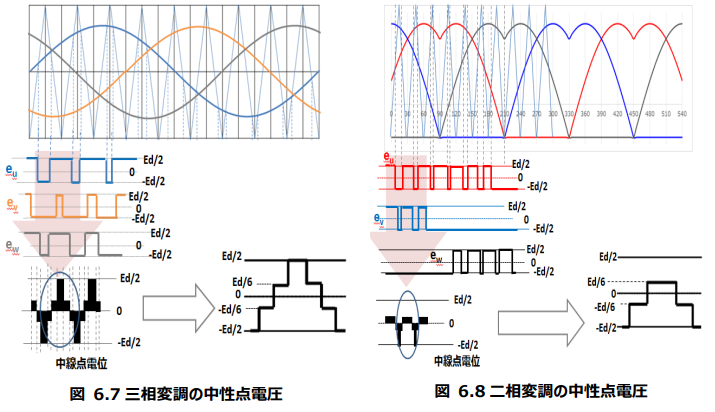
以下に模式図を示す。
二相変調は以下の特徴を持つ。
- 利用可能変調率が三相変調より大きい
- スイッチング回数が少ない(三相変調と比べて)
- 電流波形が綺麗じゃない(三相変調と比べて)
- 電気角1周期に対して、キャリアが12周期必要。(三相変調は6回)
変調率の比較を以下に示す。(三相変調:三角波比較方式)

3次高調波重畳
三相変調に対して、中性点をずらすことにより利用可能変調率を向上させる。
この方式により、二相変調と同じ利用可能変調率となる。
方形波駆動
二相変調や3次高調波重畳の三相変調よりも大きな電圧を出力できる。
以下の特徴を持つ
- キャリアを用いず、6方向にのみ電圧を印加する。
- 大きな変調率を利用できる(上図参照)
- 振動が大きい
- 電気角のみを制御する(PWM変調はパルス幅と電気角を制御する)
- PWM制御と方形波制御の切り替え時に振動が生じやすく、車両適合が難しい
- 世界中でこの手法を自動車に応用できるのはTOYOTAのみ
- ブラシレスDCモータに用いられることが多い

空間ベクトル変調
実装したことないので詳しくないが、理解できる範囲で記す。
方形波制御の場合、下図に示すようにV1~V6を出力する。それを一定時間間隔で変更する制御方法。
ベクトルの長さではなく,ベクトルの出力時間の比率と捉え、
ある時間間隔 T[s] において,インバータが V1,V2,V0 をそれぞれ個別の時間だけ出力するようにベクトルを切り替える。
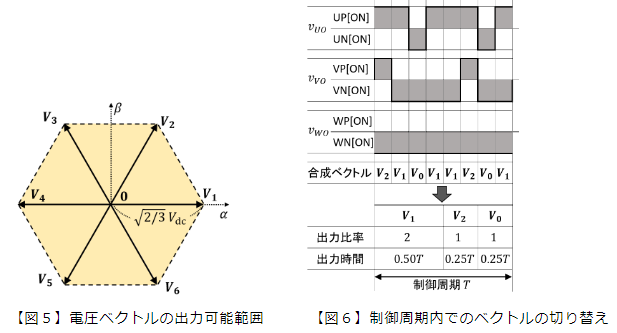
相当制御周期を早くしないと電流波形が汚そうな手法と感じる。安価なマイコンでは実現が難しそう。
参考サイト
ココまではHWエンジニアにとっての最低レベルの知識を記した。(まだシステムの観点が足りてないけど。)
ココからはSWエンジニアが開発するために必要な知識を記す。
モータ制御実装上の注意点
いつか追記する。
制御周期(割り込み)
デッドタイム補償
減磁・着磁
HiZ状態
集中巻き・分布巻き
トルク推定
キャリアの選択方法
効率
銅損・鉄損・スイッチング損
三相ON
参考図書
- 埋込磁石同期モータの設計と制御:TOYOTAのモータ制御部署でのバイブル
- 省エネモータの原理と設計法:制御工学の知見がある人はブロック線図で解説してくれるので取っ掛かり安い。
(本記事の図はこの書籍を参照) - 電力回生とエネルギー貯蔵:お値段1万円越え。
参考サイト
日本電気技術者協会
電気設備技術データーベース
私が作成したモータ適合の記事
回転磁界のwiki
大阪府立大学出身のブログ
Discussion