PID制御
制御工学を専門的に解説するサイトが最近できた(2023/4/11)ので、そちらを参照ください。
専門的で解説も丁寧なので、このページで無駄な時間を費やす必要はありません。
概要
本記事では、PID制御に関して説明する。
PID制御と記述しているが、PD制御やI-PD制御等も含む。
- PID制御とは
- 制御系の設計
- ゲインチューニング
PID制御とは
最も実用的な制御手法。世の中の制御の9割以上はPID制御だと個人的には思う。
PID制御を用いる上で最も大切なことは制御対象が線形であることである。
(制御工学における線形は周波数領域での線形である。)
制御対象が線形であれば、閉ループ(ユニティーフィードバック)系も線形となる。
閉ループの伝達関数が K(s)P(s)/(1+K(s)P(s)) となる式変形を一度は手計算で行うことをお勧めする。
古典制御では、基本的に線形しか扱うことができないことを常に留意すること。
また、理論は周波数領域/連続時間だが、現実は時間領域/離散時間を扱うことも常に頭に入れておく必要がある。
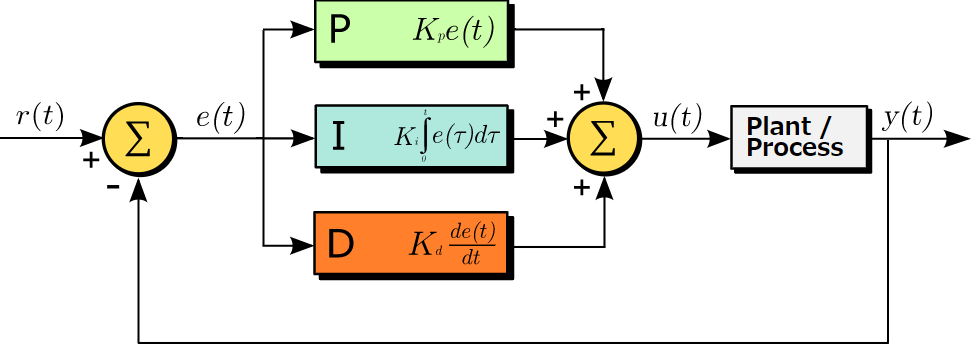
本記事では、上図を基に、以下の標記を用いる。
以下は周波数領域での標記を示す。時間領域は小文字とtでr(t)のように示す。
- 制御器:K(s)
- 制御対象:P(s)
- 参照入力:R(s)
- 誤差:E(s)
- 制御入力:U(s)
- 出力:Y(s)
制御系の設計とは
単純にPID制御器を付けるだけでは、目標の性能を達成できない。
如何にして制御系を構築するかの手法を記す。
積分項では定常偏差を減らし、微分項では応答性を上げる等の前提知識は省略する。
ゲインチューニングとは
構築した制御系のゲインをチューニングすること。
ゲインチューニングには様々な手法があり、確立された手法は存在しない。
本記事では、いくつかの手法の概要を記す。
制御系の設計
本記事は完全に個人的な経験を基から得たノウハウであり、完全に主観であることを留意頂きたい。
古典制御では、制御対象が線形である必要があります。ただ、必ずしも制御対象が線形であるとは限らない。
制御対象が非線形の場合、非線形制御を適用することもできますが、数学的に非常に難しく、実装が困難という現実がある。
これに対して、非線形の制御対象を線形になるように制御器を設計するという手法が取られる。
本記事では、そのノウハウについてまとめたものである。
(制御に一番効くのは制御周期である。基本的には制御対象の時定数の1/10未満を設定すれば問題ない。)
- 補正マップ
- 座標変換
- 非干渉制御
- マイナーループ
- 二自由度制御器
補正マップ
本手法は制御入力u(t)に対して補正を行い、制御対象P(s)を線形化する方法である。
例として、PWM制御の一例を示す。
下図のように制御器からの制御入力が制御対象のパワー素子の応答遅れにより電子負荷に対して正しく電圧が伝わらない場合を考える。
(マイコンはMOSFET、パワー素子はIGBTの場合、遅れ時間が異なる。)
パワー素子を制御器に含めるか制御対象に含めるかは制御設計次第である。
実際の制御入力であるパワー素子からの出力を観測できる場合、制御器内部に補正マップを持たせることで、制御対象の線形化が図れる。
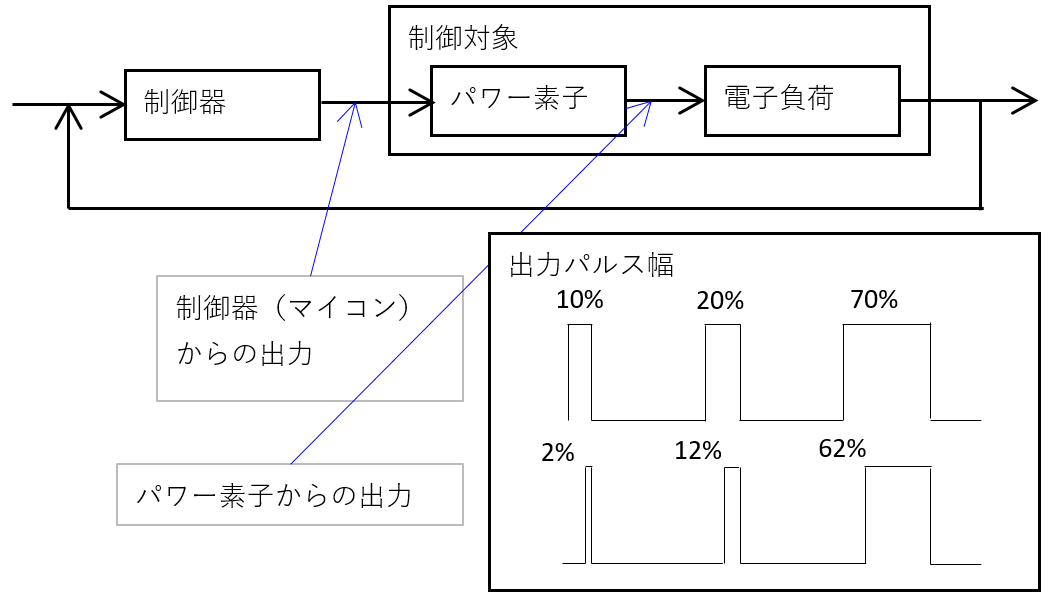
上図は一定値が常に削られているので、非干渉制御を適用するのが適当である。
座標変換(線形写像)
実際に観測される信号を別の座標に変換することで制御する手法である。
ハンマー投げを想像頂きたい。
ハンマーの軌道を観客席から操作しようとすると上下左右奥行きと3Dでの操作が必要となる。
例えば、真上から写像を取ると、上下左右の2Dでの操作が可能となる。
さらに、選手の目線からの写像を考えると、操作が必要なのは目線から高いか否かの1Dでの操作になる。
これが座標変換(線形写像)の考え方である。
次に、本手法の代表例であるベクトル制御を基に説明する。
ベクトル制御は三相交流モータ制御で用いられる手法であり、モータ制御では磁石の向きに対して電流を流す必要がある。
当然、電流は三相交流である必要があり、印加する電圧は三相交流である。
三相の電流には関連性があり、それぞれ制御することはできない。
ここで登場するのがdq変換である。dq変換は三相の電流を二相に変換する。
下図は三相のuvw電流をab変換し、さらにdq変換した図を示す。
(参考サイト:https://runge0704.hatenablog.com/entry/2021/03/13/123331)
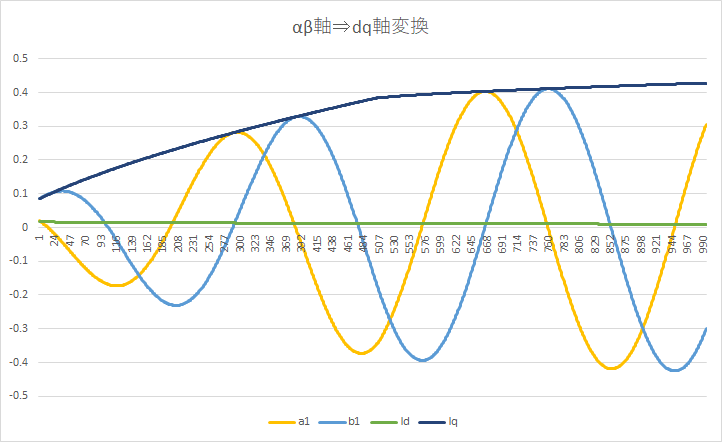
交流のab電流を直流のdq電流に変換している。行っていることは回転行列を乗算しているだけである。

上記を行った結果のブロック線図が以下である。
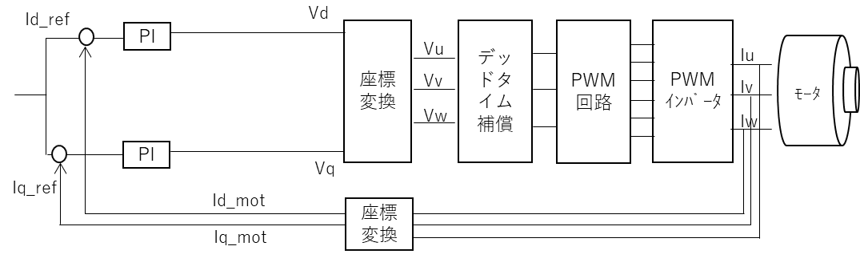
交流のuvw電流を取得し直流のdq電流に座標変換。PI制御を行い、直流のdq電圧を交流のuvw電圧に変換する。
このように座標変換を挟むことで、制御しにくい交流の信号を制御しやすい直流の信号に変換することができる。
非干渉制御
本手法は既知の非線形成分を打ち消す方法である。
上記と同様にモータ制御の例を示す。
モータ制御では、以下の電圧方程式を用いて、指令電圧を示すことができる。
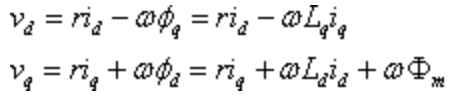
d軸の電圧Vdがd軸の電流Idのみで決まれば、制御系は線形である。
しかし、上式から分かるように誘起電圧の影響のIqが入っており、非線形になっている。
この非線形の項を打ち消すのが、非干渉制御である。非干渉制御を行い、誘起電圧項を打ち消した結果が以下である。

上記の非干渉制御を適用した制御系が以下である。

マイナーループ
本手法が最も一般的な手法だと考える。重要なのは、内側のループと外側のループで制御周期が異なることが多いことである。
先にモータ制御の速度制御のブロック線図を示す。

モータを指定速度で回転させたい。モータの場合、制御入力は電圧であるが、電圧と回転速度に線形性はない。
トルクと電流には周波数依存性がなく、電流と電圧にも先の手法を用いれば線形性を持たせることができる。
この関係性を基に非線形な制御対象を線形に近づけたのが上図である。
回転速度は外乱トルクに依存するため、外乱オブザーバを用いて非干渉制御を行うと線形性が向上する。
正直、回転速度の時定数が遅いので、そこまでする必要があるかは疑問。
二自由度制御器
ここまでユニティーフィード系のPID制御について述べたが、
応答性を上げるためにゲインを大きくすると、発散しやすくオーバーシュートが大きくなるという欠点がある。
これに対処するための手法が二自由度制御器である。

フィードフォワード要素を事前に加えることで、フィードバックゲインを小さくすることができ、
所望の応答特性を得ることができる。
詳細は以下のサイトや「フィードバック制御入門」を参照すること。
ゲインチューニング
ゲインチューニングは以下の手法が知られている。
そのうち利点・欠点を表にまとめる。
- 制御対象の数式モデルが既知の方法
- モデルマッチング法
- 周波数特性を用いる方法
- 制御対象の数式モデルが既知でない方法
- ジーグラ・ニコルスのPID調整法
- 限界感度法
- ステップ応答法
- 入出力データを用いる方法
- 制御対象を数式モデル化する方法
- システム同定
- 直接制御器を調整する方法
- VRFT、FRIT
- 制御対象を数式モデル化する方法
- 反復法
- ジーグラ・ニコルスのPID調整法
制御対象の数式モデルが既知である方法
モデルマッチング法
規範モデルを用いて、その規範モデルが望ましい特性を持つように極配置を行う。
詳細は以下の動画や「倒立振子で学ぶ制御工学」を参照すること。

周波数特性を用いる方法
一巡伝達関数のゲイン余裕と位相余裕を経験的に求められた値になるように制御器を設計する。
詳細は以下のサイトや「制御工学の基礎(森北出版)」を参照すること。
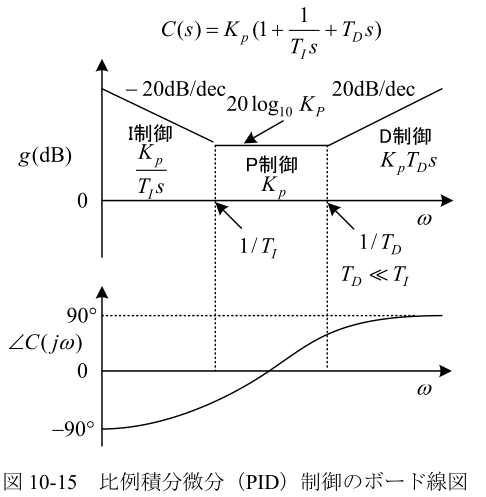
制御対象の数式モデルが既知でない方法
ジーグラ・ニコルスのPID調整法
以下の資料が分かりやすいので、詳細は以下の資料を参照すること。
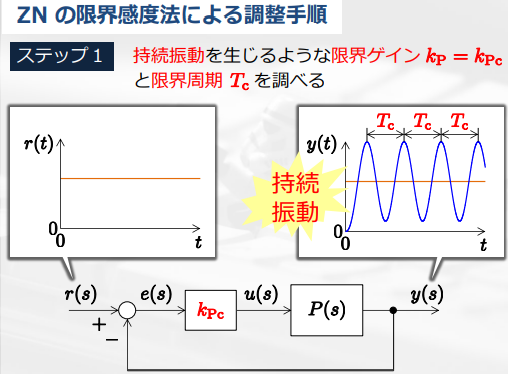
限界感度法
制御対象に対して、P動作単体で動作させ、Pゲインを持続振動まで大きくする。
このときのPゲインと振動周期から、PIDゲインを決定する。

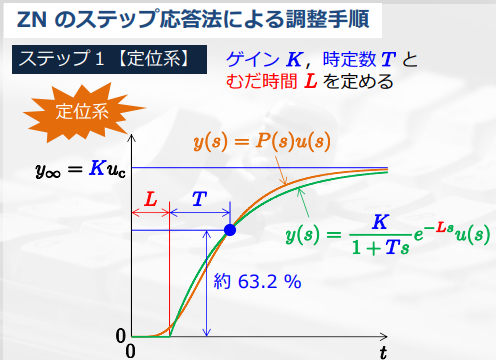
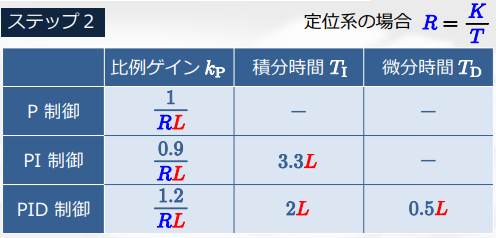
ステップ応答法
制御対象に対してステップ入力を印加し、その時の応答を計測する。
このときのゲインと時定数から、PIDゲインを決定する。
入出力データを用いる方法
システム同定
スイープ信号やM系列データを制御対象に入力し、出力を計測する。
(これはシステムの伝達関数を求めるため、入出力にあらゆる周波数を含む必要があるため。)
取得した入出力データを用いて、制御対象の数式モデル化を行う。
予め数式モデルの形式を決め、その係数を同定することが多い。
MATLABのsystem identification toolboxを用いたシステム同定しか経験がないので、加筆求む。
同定後は、他の手法を用いてゲインを決定する。
詳細は以下の資料を参照すること。

VRFT、FRIT
制御対象の数式モデルが既知である方法のモデルマッチング法を制御対象の入出力データを用いて実現する方法。
基本思想はシステム同定と同様だが、制御対象の数式モデルを導出せずに、直接制御器のゲインを決定する。
予め制御器の形を決め、そのゲインをチューニングする。
仮想(疑似)参照入力という概念を用いて、入出力データから成る評価関数を最小化するゲインを最適化により求める。
詳細は以下の資料を参照すること。

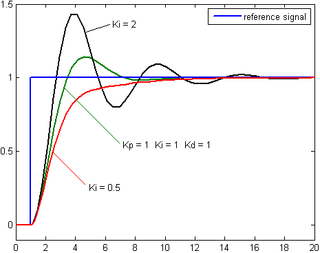
反復法
試行錯誤によりゲインを決定する。
知識を必要としないが、コツを紹介する。
- 制御器の単位変換によって、Pゲインを大まかに決める。
ex. 制御器からの電流[A]をセンサが取得する。それにゲインを乗じて、電圧[V]を出力する。
制御対象の抵抗のオーダー次第に応じて、Pゲインを設定できる。
このように制御器と制御対象の単位を把握することで、大まかなPゲインを決定できる。 - Pゲインを調整する
- Iゲインを調整する。このとき、積分項のグラフも表示すること。
- Dゲインを調整する。このとき、微分項のグラフも表示すること。
Discussion