進化計算コンペティション2023に挑戦した話
この記事は進化計算学会によって毎年行われている、現実での課題に沿った最適化問題でコンペを行う「進化計算コンペティション」の2023年開催コンペに挑んでみたものです。
進化計算とは?
進化計算は組み合わせ問題の最適化としてよく使われる手法です。
例えば、小学生の遠足のおやつを思い浮かべてください。おやつ購入の上限を300円までとしたときに、以下のおやつがあったら何が最適解でしょうか?

どうでしょう。パッと思いつくのはチョコ100円、グミ200円の組み合わせでしょうか。
ただ、これをどうやって選択したかと考えるとなかなか難しいものではないでしょうか?(脳内で高速に総あたりした?もしくは1+2=3という簡単な計算をこの問題に当てはめた?など色々考えられますね。)
かなり小規模な問題ですが、これも様々な組み合わせの中から最適解を選ぶ、組み合わせ最適化と言えます。
では、進化計算ではどのように解くのでしょうか。手法にもよりますが、多くはいくつか答えを作っておいて、その評価が高い答えの要素を組み合わせる・変化させる等で次の答えを機械的に求めて行くと思います。
例えば以下のフローのようになります。
- 1つ目: せんべい(15円)を選んでみる、2つ目:グミ(200円)を選んでみる。
- 1つ目と2つ目を比較して、2つ目のほうが300円に近い!
- 2つ目のグミ(200円)を生き残らせ、チョコ(100円)を入れてみる。
- ちょうど300円で最適解!
フローを見ると、優秀な答え(2つ目)が生き残っていますよね。
これが「進化」計算の由来となっています。
簡単な例でしたが、もっと複雑な問題に対しても同じようなフローで解を見つけることができるわけです。
今回の課題
今回のコンペ課題として「自動化が進んだ製造工場における機械加工スケジューリング問題」が出題されました。
今回は自動化が進んだ製造工場における機械加工スケジューリング問題を出題します.
現在,産業界では,少子化や若者のものづくり離れなどの影響による人手不足が問題となっています.そのため,人手不足を補うために,デジタル技術を活用した生産工程の自動化が進められています.しかし,作業者と自動処理可能な機械が混在する実際の製造現場では,作業者の休憩時間や機械の稼働時間など様々な制約が存在します.そのため,多制約最適化問題のための効率的な最適化手法の開発が期待されています.
このような背景をもとに本コンペティションでは実際の製造現場で起こっている問題を取り上げ,良質なスケジュールの導出を目指してもらいます.
公式説明のように、車の製造工場のような労働者による手作業と機械が行う自動化された作業が存在する現場は多々あるかと思います。
その中で、どのような順番で作業するのが最も効率的にできるかをという問題が存在し、さらに制約が加わることで実際に可能なスケジューリングを探し出すのは不可能に近い場合も多い、というのが今回の問題設定です。
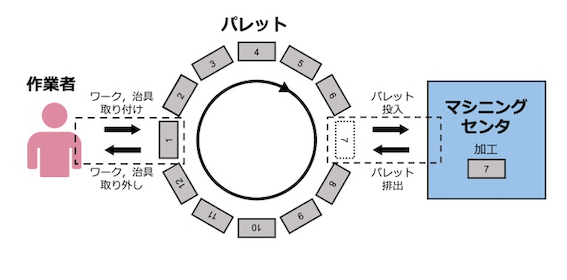
(公式サイトより)
課題は単目的・多目的の部門に分かれており、今回自分は両方とも挑戦してきました!
単目的部門への挑戦
機械加工スケジュールの最適化では考えねばならない様々な要素がありますが、今回の課題に関しては運営さんが用意してくれたSCIPというリゾルバが大部分を自動で解決してくれるという作りになっていました。
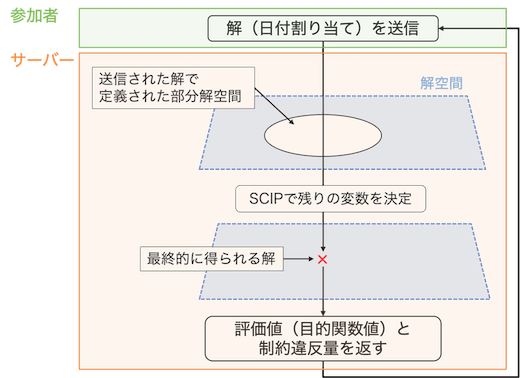
(公式サイトより)
ただし大事な要素として、機械による加工を行うための対象物の取付と加工後の取外を行う必要があるため、単目的部門では作業者がその作業を行うスケジュールを決定します。
アプローチ方法
前提の中にある通り、今回の課題はジョブショップ・スケジューリング問題とみなすことができます。
この場合、重要となってくるのは 「全体の業務におけるクリティカルパス」 です。
https://next-sfa.jp/journal/skill/criticalpath/
クリティカルパスを一言で説明すると、
プロジェクトを進めていく上でスケジュールに影響が出る作業経路のことを指します。
そこで、今回の問題で以下2点に着目して見ると良いのではないかと考えたわけです。
- 取付から取外を行うまでの各作業期間
- 取付を行う際の各作業開始時間(優先度)
この2点は以下の画像のように2軸をそれぞれ割り当てて、プロットする事も可能です。
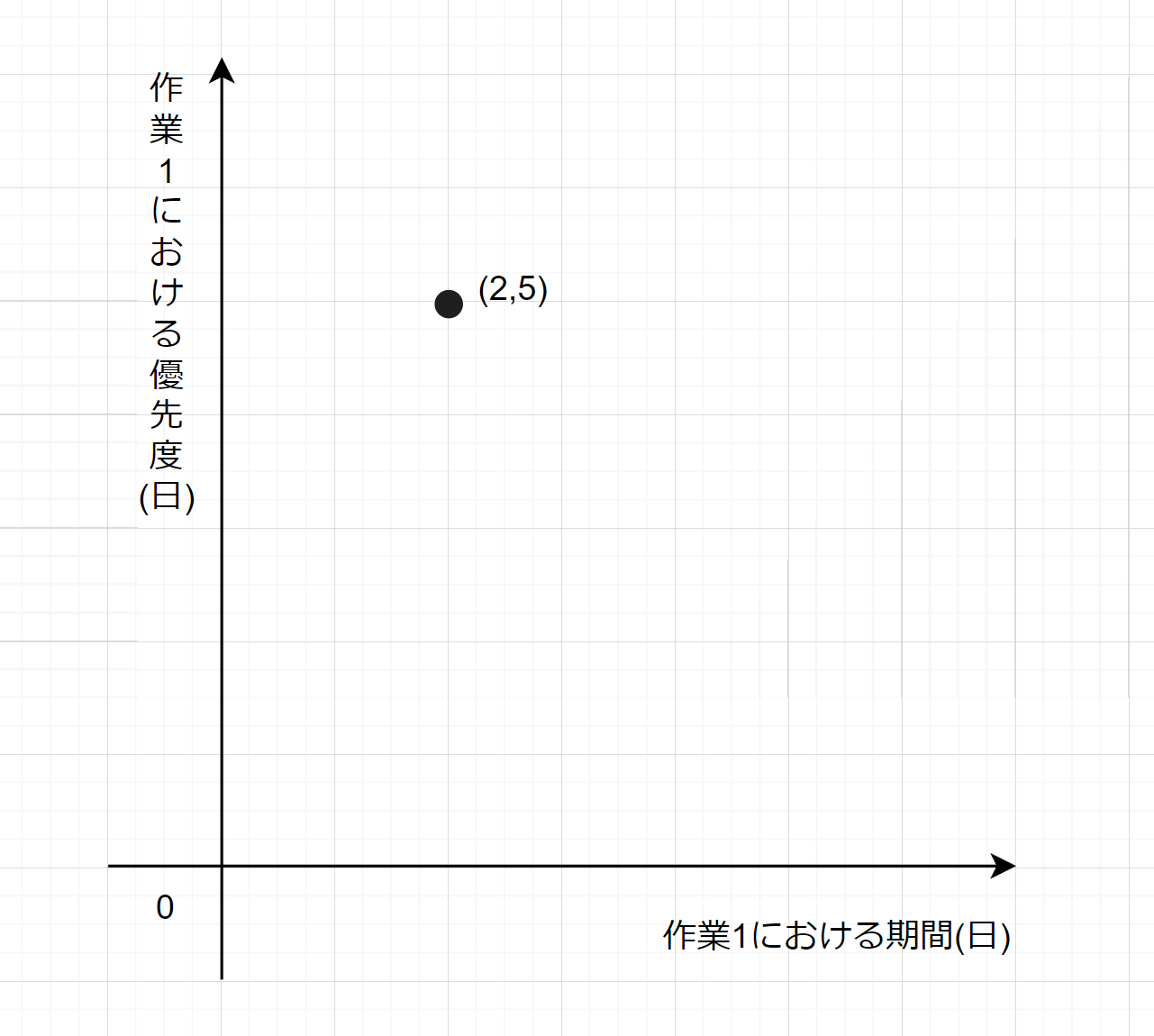
さらに、思いついたのはこれを活用してクラスタリングを行うことです。
実は進化計算を行う中で重要な問題として、局所解に陥りがちという点が挙げられます。これをk-means法を活用してクラスタから類似性の低い解を選択することで解決できるのではと考えました。
また、進化計算手法として遺伝的アルゴリズムを組み合わせました。遺伝的アルゴリズムは汎用性が高く、解を探索する上で範囲を絞るのも早いので、最適解に辿り着きやすいと考えたわけです。解探索のイメージは以下のとおりです。
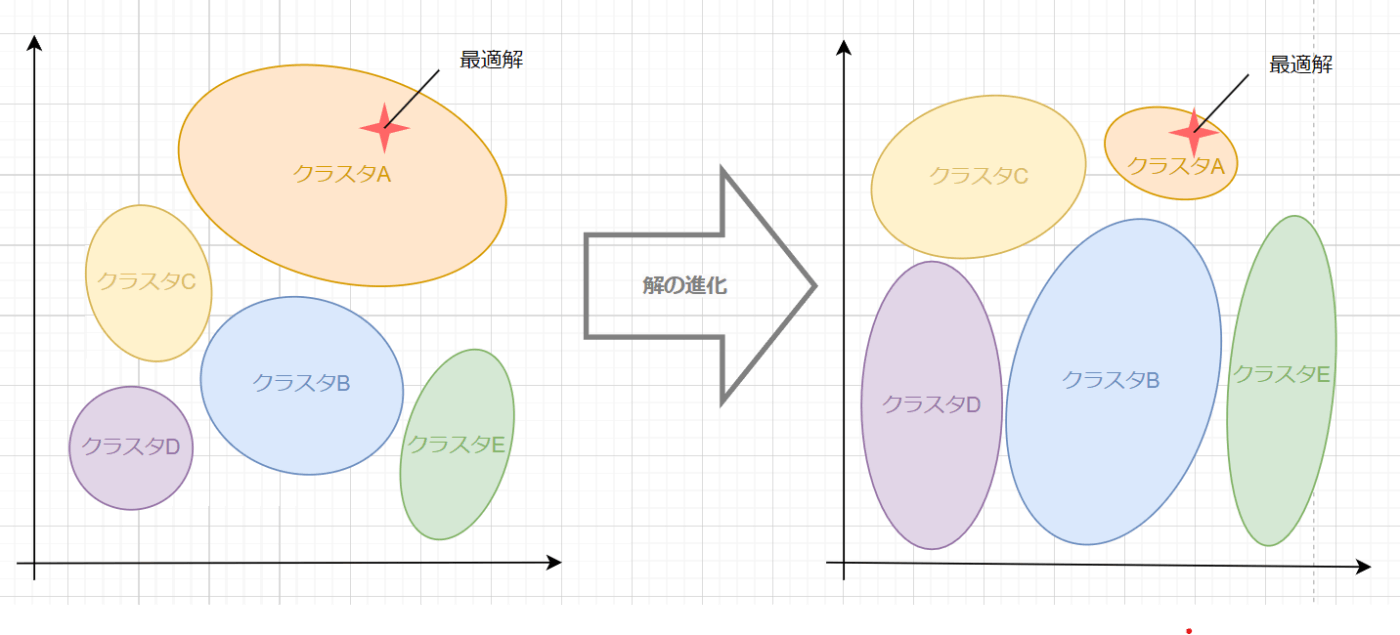
つまり、今回の手法は遺伝的k-means法ということです。
具体的なアルゴリズム
具体的なアルゴリズムのフローとしては以下の通りです。
- 最初に1000個の個体をランダムに生成しておく。
- 各個体の各作業における期間・優先度同士を以下の式のようにユーグリッド距離に従って算出し合計を求める。これを元に個体同士の類似度を求め、最終的に20個のクラスタを生成する。
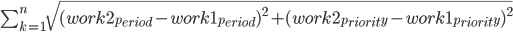
- 各クラスタから1つずつ、計20個になるまでランダムに個体を抜き出す。
- 抜き出した個体を評価する。
- 90%の確率で、個体の評価結果からルーレット選択によって2つの選択して3点交叉により新規個体を生成する。また10%の確率で、突然変異を行い完全にランダムな新規個体を生成する。
- 計20個の個体を生成し、クラスタから抜き出した分の個体と交換する。
- 2に戻る。
今回の解評価の上限回数は1000回であったため、50回進化することができます。
検証結果
単目的部門の練習問題が用意されているため、それを使って検証を行ってみました。横軸を進化回数、縦軸を進化回ごとの評価値の平均としてグラフにしました。結果は以下の通りです。
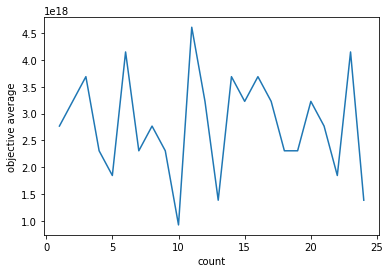
見て分かる通り、解が収束していません。おそらく乱数で生成したものとほとんど変わらないぐらい分散しているのではないでしょうか。
なぜこのようになったか、原因はいくつか考えられるのですが、特に大きいのは 「1000個体をランダムに生成して20個ずつが進化していくので、進化速度が非常に遅い」 点が挙げられると思います。
これを回避するには、
- 比率として1000個体は多い(元のクラスタに全然影響が出ない)ので減らす
- 評価した解から全く新しいクラスタを作り上げる。
等が考えられます。何にせよ、根幹から作り直す必要がありそうでした。
多目的部門への挑戦
多目的部門の前提は単目的部門とほとんど同じですが、加えて評価軸が4つに増えます。
- 納期余裕の最大化
- メイクスパンの最小化
- 納期遅れの最小化
- 残業時間の最小化
そのため、どれをどのくらい重視するかという重みについても自分で決めて最適化をしていきます。
アプローチ方法
アプローチ方法は単目的とほとんど変わりません。重みが加わったので重み同士のプロットを行いクラスタリングの要素として含めました。
検証結果
同様に多目的部門用の練習問題が存在しているため、そこで検証をしました。こちらでは、横軸を進化回数、縦軸を最高得点としてグラフにしました。結果は以下のとおりです。

見て分かる通り、点数はずっと0点のままでした。4つの評価点のうちどれが原因になっているかというと「残業時間の最小化」です。(逆にそれ以外は多かれ少なかれ点数は出ているようでした。)
局所解に陥らないように、初期段階で最低限の制約のもとランダムに生成している解を使っていたのですが、どうやらそれが裏目に出たようです。そもそも実行可能解を探し出すのがかなり難しいようでした。
シンプルな対策としては 「最初から制約で解の探索範囲を狭めておく」 ことかなと思います。局所解に陥りやすくはなりますが、今回のような評価回数が少ない問題に関しては有効かなと感じました。
感想
実はこれで参加するのは計4回目なのですが、毎回参加するときに
- 進化計算を使うこと(実はこのコンペは進化計算学会が主催ですが、進化計算の手法を使わなくても良いです)
- 問題ごとの設定に依存せず、なるべく汎用的になるように設計すること
という縛りを勝手に自分に課しています。
理由は進化計算で結果を出してみたいというのと、現実問題で使うならば汎用的にしておいたほうが将来性があると思っているからです。(他の研究に応用される面も含めて)
そんな中、今回は他の方と大きく異なったアルゴリズムを考えつくことができたため、自分的には非常に満足のゆく結果でした。実際コンペの発表会でも説明を聞いた方から他にない発想で面白いと評価いただけました。
ただ結果が出なかったので非常に残念でした。汎用なリゾルバを目指すと最適解にたどり着くまでの速度が遅くなりがちではありますね。
引き続き諦めずに、このコンペには他の方とは違った自身の奇抜なロジックで挑戦し続けていきたいと思います!
この記事を読んで、興味が出た・やってみたいと思った方も進化計算コンペティションにぜひ挑戦してみてください!
ちなみに、コードは以下で公開しております。


Discussion