🤖
ReLUと初期値〜ディープラーニングにおける活性化関数のふるまいと工夫〜

2025/04/15に公開
 はじめにいずれ自身の役に立つと考え、ディープラーニングの学習を始めました。まずは画像識別器の作成を目指し、CNN（畳み込みニューラルネットワーク）のお手本を探して実装しました。

CNNの構成要素である畳み込み層では、画像が持つさまざまな特徴を抽出します。そしてその出力を処理するのが活性化関数です。活性化関数には複数の種類がありますが、参考にしたモデルでは ReLU（Rectified Linear Unit） が用いられていました。

学習を進める中で、なぜReLUがよく使われるのか？ReLUを使う際の初期値設定の重要性は？という点に興味を持ったため、実際に手を動かして調べてみました。

 ReLUのふりかえりReLUは非常にシンプルな非線形関数で、次のように定義されます。
ReLU(x)={xif x≥00if x<0
\text{ReLU}(x) =
\begin{cases}
x & \text{if } x \geq 0 \\
0 & \text{if } x < 0
\end{cases}
ReLU(x)={x0​if x≥0if x<0​​

これにより、ネットワークに非線形性を与えつつも、計算が軽量で扱いやすいため、多くの深層学習モデルで使われています。

 単層・5層の出力を観察するReLUの性質をより深く理解するために、単純な1層のネットワークと5層のネットワークを構成して、出力の分布を観察してみました。
import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt

torch.manual_seed(0)
x = torch.randn(1000, 100)
linear = nn.Linear(100, 100)
relu_y = F.relu(linear(x))

plt.xlim(-0.1, 4)
plt.hist(relu_y.detach().numpy().flatten(), bins=30, color='blue', alpha=0.7)
plt.title("ReLU with std=1 initialization (1 layer)")
plt.xlabel("Output Value")
plt.ylabel("Frequency")
plt.grid(True)
plt.show()
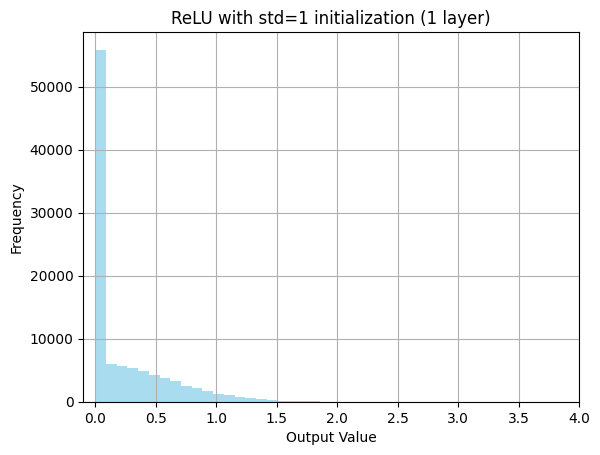
出力を確認すると、0に近い値が非常に多く、右に裾を引いた分布になっています。ReLUは負の値をすべて0にするため、活性化される（= 0より大きくなる）割合はそれほど多くありません。

層を増やすとどうなるか？次に、層を5層に増やして同じく標準的な初期化（平均0・分散1）を使った場合を見てみます。
def build_relu_mlp(layers=5):
    net = []
    for _ in range(layers):
        layer = nn.Linear(100, 100)
        net.append(layer)
        net.append(nn.ReLU())
    return nn.Sequential(*net)

torch.manual_seed(0)
x = torch.randn(1000, 100)
model = build_relu_mlp(layers=5)
outputs = []

with torch.no_grad():
    for layer in model:
        x = layer(x)
        if isinstance(layer, nn.ReLU):
            outputs.append(x)

fig, axes = plt.subplots(nrows=5, ncols=1, figsize=(8, 12))
for i in range(5):
    ax = axes[i]
    ax.hist(outputs[i].detach().numpy().flatten(), bins=30, color='lightcoral')
    ax.set_title(f"Layer {i+1} - ReLU with std=1 init")
    ax.set_xlabel("Output Value")
    ax.set_ylabel("Frequency")

plt.tight_layout()
plt.show()
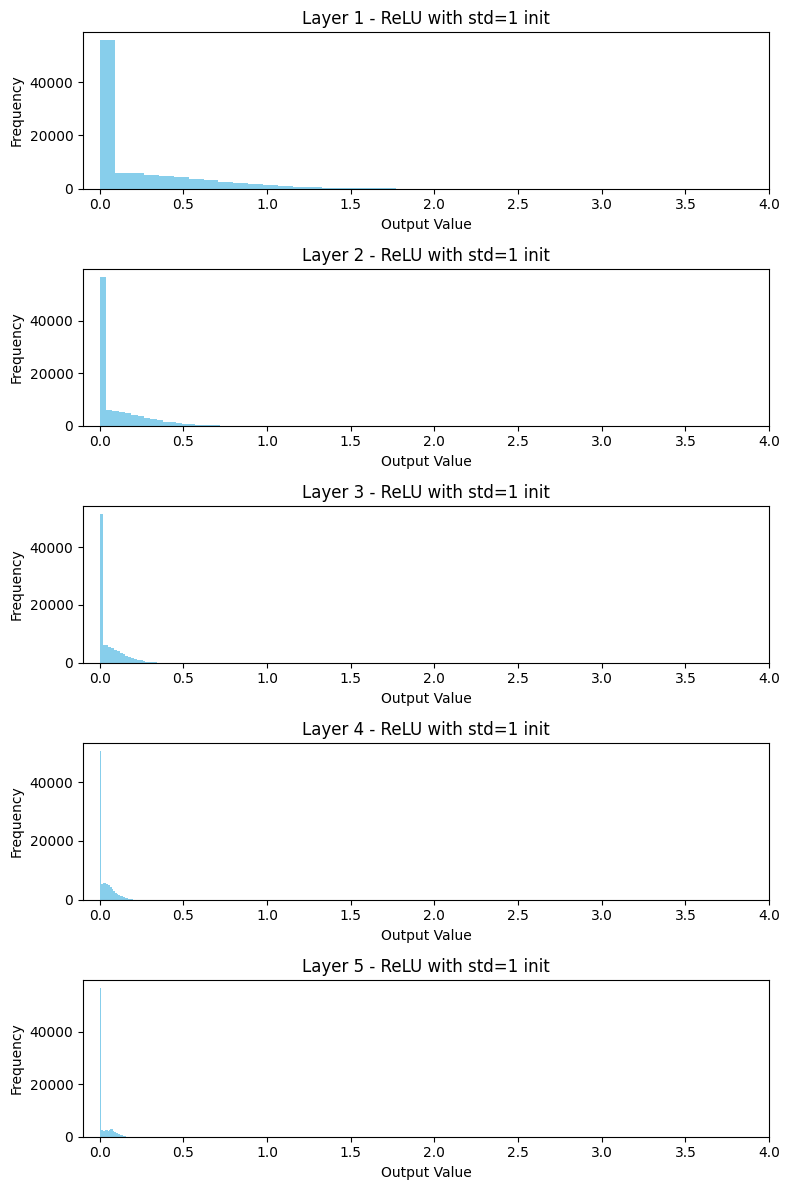
出力を確認すると、層が深くなるにつれて出力がほとんど0に集中していく傾向が見られました。やはりこれは、ReLUが負の値を切り捨てる性質によるものと考えられます。

 Heの初期化について調べるこのような問題を防ぐために、活性化関数に応じた適切な初期値の工夫が必要になります。ReLUに対しては、「Heの初期化（He Initialization）」が提案されています。Heの初期化では、重み WWW を以下のように初期化します：
W∼N(0,2nin)
W \sim \mathcal{N} \left(0, \frac{2}{n_{\text{in}}} \right)
W∼N(0,nin​2​)ここで ninn_{\text{in}}nin​ は前の層のノード数です。この方法では、層を通過するごとに出力の分散が小さくなりすぎないよう調整されており、情報の流れが保たれやすくなります。以下は、He初期化を適用した5層のネットワークで、出力分布を可視化した結果です。
def build_he_mlp(layers=5):
    net = []
    for _ in range(layers):
        layer = nn.Linear(100, 100)
        nn.init.kaiming_normal_(layer.weight, nonlinearity='relu')  # He初期化
        nn.init.zeros_(layer.bias)
        net.append(layer)
        net.append(nn.ReLU())
    return nn.Sequential(*net)

torch.manual_seed(0)
x = torch.randn(1000, 100)
model_he = build_he_mlp(layers=5)
outputs_he = []

with torch.no_grad():
    for layer in model_he:
        x = layer(x)
        if isinstance(layer, nn.ReLU):
            outputs_he.append(x)

fig, axes = plt.subplots(nrows=5, ncols=1, figsize=(8, 12))
for i in range(5):
    ax = axes[i]
    ax.hist(outputs_he[i].detach().numpy().flatten(), bins=30, color='skyblue')
    ax.set_title(f"Layer {i+1} - ReLU with He init")
    ax.set_xlabel("Output Value")
    ax.set_ylabel("Frequency")

plt.tight_layout()
plt.show()
結果として、層を通過しても出力分布が極端に偏ることなく、情報がしっかりと保たれていることが確認できました。

 おわりに今回、ReLUというシンプルな活性化関数がなぜ深層学習でよく使われるのか、そしてそれを使用する上で重要になる「初期値設定」について学びました。ReLUは計算が軽く、非線形性を持ちつつも扱いやすい。しかし、適切な初期値を設定しないと、層を深くするにつれて出力が0に偏り、学習が進まなくなる。この問題を防ぐために、「Heの初期化」という手法があり、ReLUと非常に相性が良い。単に理論を読むだけでなく、自分の手で実験を通して理解することで、より深く納得できる学びになりました。今後は BatchNorm などの正規化手法とも併せて、さらに深層モデルの安定化について探っていきたいと思います。
Discussion

ログインするとコメントできます