ゼロからのTransformer

もはや機械学習の汎用アーキテクチャと化したTransformerですが、ゼロから丁寧に解説をしている英文記事を発見したので、DeepL、みらい翻訳の力も借りつつ日本語に翻訳してみました。

元記事:
Brandon Rohrer, Transformers from Scratch, https://e2eml.school/transformers.html

なお、元記事はCC0のパブリック・ドメインです。この翻訳記事も元記事に敬意を表してCC0とします。

---

私は数年間、Transformerへの深入りを先延ばしにしてきました。最終的には、Transformerの特徴を知らないことへの不快感が、私にとってあまりにも大きくなりました。これはその深入りです。

Transformerは、2017年の論文で、あるシンボル列を別のシンボル列に変換する「配列変換」の道具として導入されました。最も有名な例は、英語からドイツ語のような翻訳です。また、系列の補完（最初の指示が与えられたら、同じ流れやスタイルで続けること）を行うためにも改良されました。今や自然言語処理の研究や製品開発に欠かせない道具となっています。

始める前に注意しておきたいことがあります。ここでは、行列の乗算や誤差逆伝播法（モデルを学習するためのアルゴリズム）についてたくさん話しますが、事前に知っておく必要はありません。必要な概念を1つずつ、説明しながら追加していきます。短い旅ではありませんが、来てよかったと思っていただけるようにしたいと思います。

• One-hot表現
• 内積
• 行列の乗算
• 表探索としての行列の乗算
• 1次系列モデル
• 2次系列モデル
• スキップ付き2次系列モデル
• マスキング
• 休憩所と出口ランプ
• 行列の乗算としてのattention
• 行列の乗算としての2次系列モデル
• 系列補完
• 埋め込み
• 位置エンコーディング
• 脱埋め込み（De-embeddings）
• Softmax
• Multi-head attention
• Single head attention再訪
• スキップ接続
• 層の正規化
• 複数の層
• デコーダースタック（Decoder stack）
• エンコーダースタック（Encoder stack）
• Cross-attention
• 字句解析
• バイト対符号化
• 音声入力
• まとめ
• リソースとクレジット

one-hot表現

初めに言（ことば）たちがあった。^[1] 非常に多くの言葉がありました。私たちの最初のステップは、すべての言葉を数値に変換して、計算できるようにすることです。

私たちの目標が、声で命令するコンピュータを作ることだと想像してみてください。私たちのやることは、一連の音を一連の言葉に変換（convert）（または 変換（transduce））^[2] する変換器（transformer）を作ることです。

まず、語彙（vocabulary） を選ぶことから始めます。語彙とは、各系列で扱うシンボルの集合体です。ここでは、シンボルの2つの異なる集合を用意します。1つは音声を表す入力の系列用、もう1つは単語を表す出力の系列用です。

ここでは、英語を扱うことを想定してみましょう。英語には数万語の単語があり、さらにコンピュータ特有の用語を含めると恐らく数千語になります。そうすると、語彙の数は10万以上になります。単語を数値に置き換える方法のひとつは、1から数え始めて、それぞれの単語に番号をつけることです。そうすれば、一連の単語は数値の羅列として表現できます。

例えば、filesとfind、myという3つの語彙を持つ小さな言語を考えてみましょう。それぞれの単語を数値に置き換えて、files = 1, find = 2, my = 3 とすることができます。そうすると、「Find my files」という文は、[find, my, files]という単語の並びではなく、[2, 3, 1]という数値の並びで表すことができます。

このように、シンボルを数値に変換する方法は非常に有効ですが、コンピュータにとってさらに扱いやすい別のフォーマット、one-hot表現（one-hot encoding） があることが知られています。one-hot表現では、シンボルは語彙の長さと同じ長さのほとんどが0たちの配列で表され、1つの要素だけが1の値を持ちます。配列の各要素は別々のシンボルに対応しています。

one-hot表現を別の角度から考えると、各単語にはそれぞれ番号が割り当てられていますが、その番号は配列へのインデックスになっています。先ほどの例をone-hot表記にすると、次のようになります。

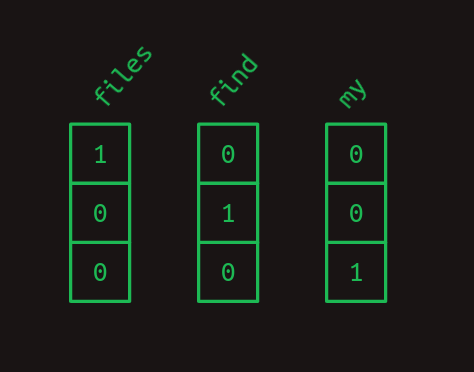
つまり、「Find my files」という文章は1次元配列の系列になり、それを圧縮すると2次元配列のように見えてくるのです。

これから、「1次元配列」と「ベクトル」という用語を同じ意味で使うことに注意してください。「2次元配列」と「行列」も同様です。

内積

one-hot表現のとても便利な点は、内積（dot product）を計算できることです。^[3]これは、内積（inner product）やスカラー積などの気の遠くなるような名前でも知られています。2つのベクトルの内積を求めるには、それぞれの要素を掛け合わせ、その結果を足します。

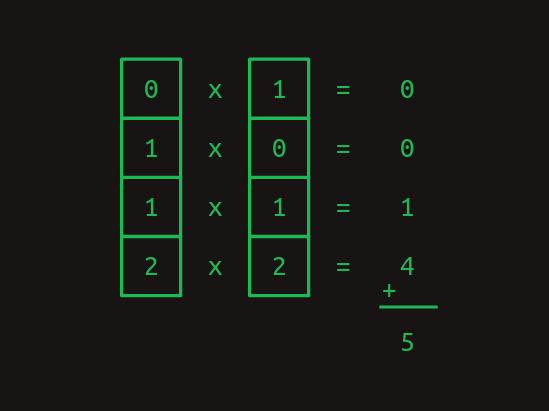
内積は、one-hot単語表現を扱うときに特に役立ちます。任意のone-hotベクトルとそれ自身との内積は1です。

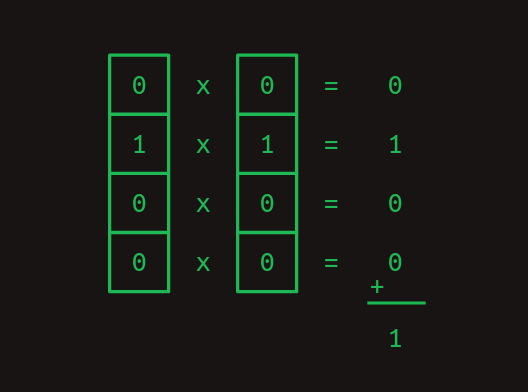
また、任意のone-hotベクトルと他の任意のone-hotベクトルの内積は0です。

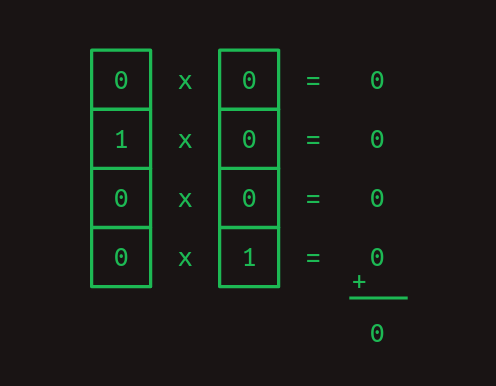
前の2つの例では、内積を使って類似度を測る方法を示しました。別の例として、異なる重みを持つ単語の組み合わせを表す値のベクトルを考えてみましょう。one-hotで符号化された単語を内積で比較することで、その単語がどれだけ強く表現されているかを知ることができます。

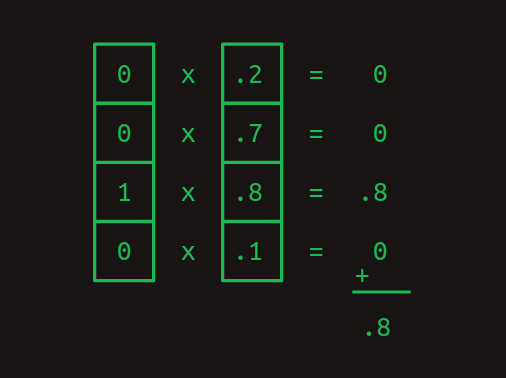
行列の乗算

内積は行列の乗算の構成要素であり、2次元配列のペアを組み合わせる非常に特殊な方法です。ここでは、最初の行列を$A$、2番目の行列を$B$と呼びます。最も単純な場合では、$A$が1行しかなく、$B$が1列しかない場合、行列の乗算結果は2つの内積になります。

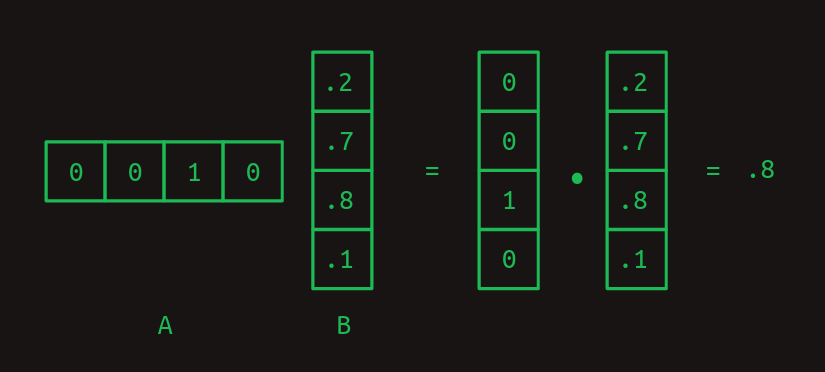
Aの列数とBの行数は、2つの配列を一致させ、内積を計算するためには同じである必要があります。

$A$と$B$が大きくなり始めると、行列の乗算を計算するのに頭がクラクラし始めます。$A$の複数の行を扱うには、それぞれの行と$B$の内積を別々に取ります。答えは$A$と同じ数の行を持つことになります。

$B$がより多くの列を占める場合、それぞれの列と$A$の内積を取り、その結果を連続する列に積み重ねます。

ここで、$A$の列数が$B$の行数と同じである限り、これを任意の2つの行列の乗算に拡張できます。この結果は、$A$と同じ行数、$B$と同じ列数になります。

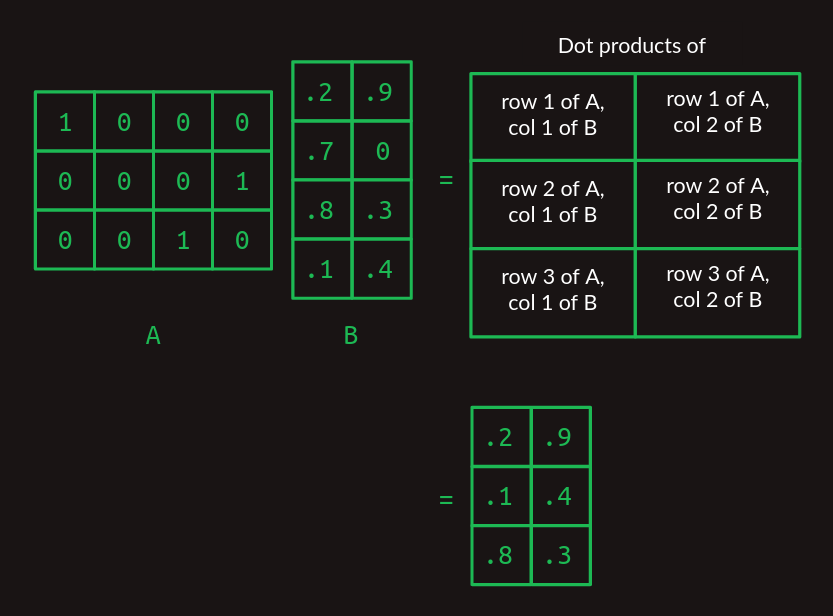
これを初めて見るのであれば、不必要に複雑に感じるかもしれませんが、後で効果があることをお約束します。

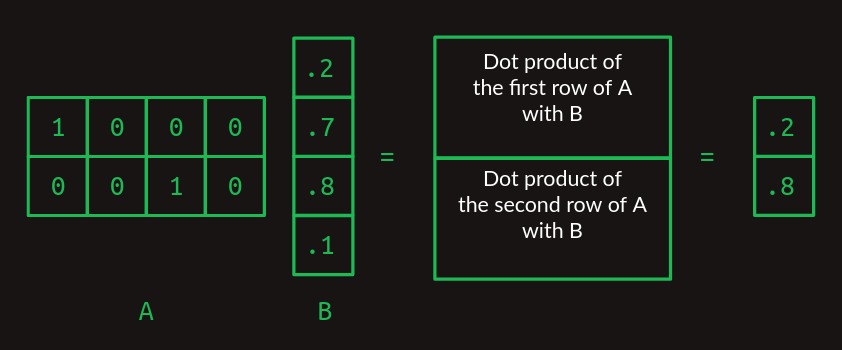
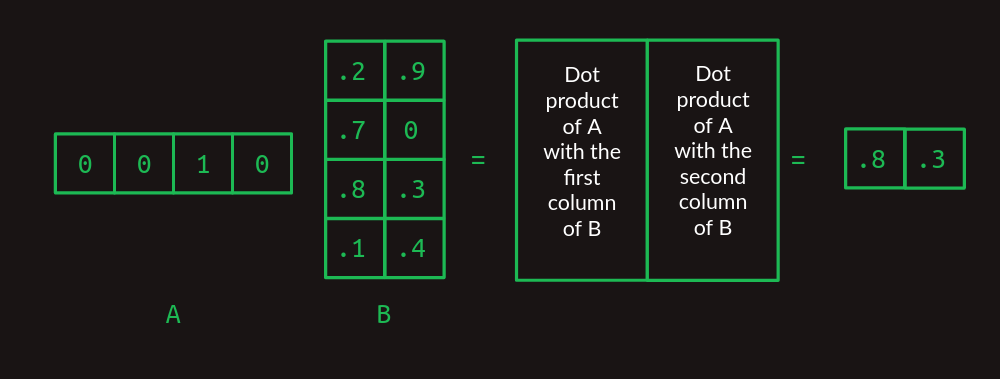
表探索としての行列の乗算

ここでは、行列の乗算がルックアップテーブルとして機能することに注目してください。行列$A$は、one-hotベクトルのスタックで構成されています。それぞれ、1列目、4列目、3列目に$1$を持っています。行列の乗算を行う際には、行列$B$の1列目、4列目、3列目の順に取り出すことができます。このように、one-hotベクトルを使って行列の特定の行を取り出すというトリックは、Transformerの仕組みの中核をなすものです。

1次系列モデル

行列のことはちょっと置いておいて、私たちが本当に関心を持っていること、つまり単語の配列に戻りましょう。自然言語のコンピュータインターフェースの開発を始めるにあたり、3つの選択肢しかないコマンドを扱いたいと想定してみましょう:

• Show me my directories please.
• Show me my files please.
• Show me my photos please.

語彙の大きさは7です:
{directories, files, me, my, photos, please, show}

系列を表す便利な方法の1つは、遷移モデルを使用することです。語彙中のそれぞれの単語について、次の単語が何である可能性が高いかを示します。ユーザーらが写真（photos）について質問する頻度が半分、ファイル（files）について質問する頻度が30％、辞書（directories）について質問する頻度が残りの場合、遷移モデルは次のようになります。任意の単語からの遷移の合計は、常に$1$になります。

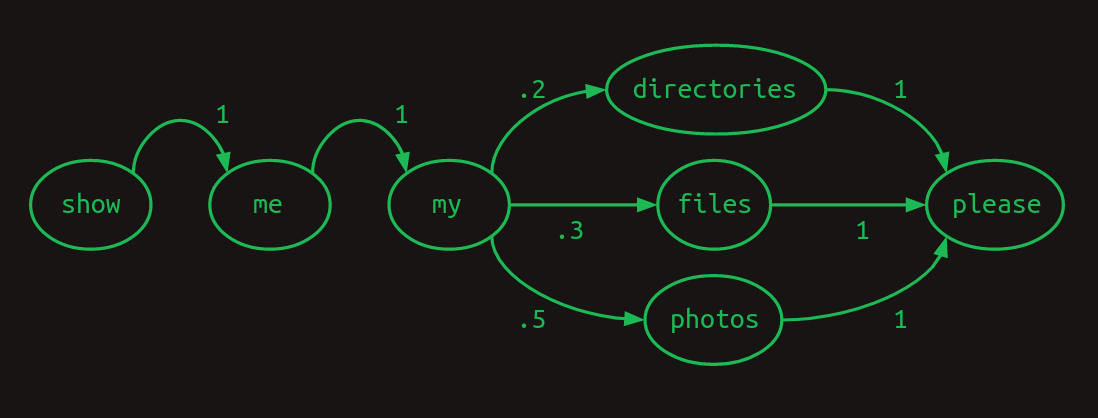
この遷移モデルは、次の単語の確率が最も直近の単語にのみ依存するというマルコフ性を満たすため、マルコフ連鎖と呼ばれています。より具体的には、1つの最も直近の単語だけを参照するため、この場合1次マルコフモデルです。最も直近の2つの単語を考慮すると、2次マルコフモデルになります。

行列からの休憩は終わりです。マルコフ連鎖は、行列形式で簡単に表現できることが知られています。one-hotベクトルを作る時に使ったのと同じインデックス体系を使うことで、それぞれの行が語彙中の単語の1つを表します。それぞれの列も同様です。行列遷移モデルでは、行列をルックアップテーブルとして扱います。関心のある単語に対応する行を探してみましょう。それぞれの列の値は、その単語が次に出てくる確率を示しています。行列のそれぞれの要素の値は確率を表しているため、すべて$0$から$1$の間を取ります。確率の合計は必ず$1$になるため、それぞれの行の値の合計は必ず$1$になります。

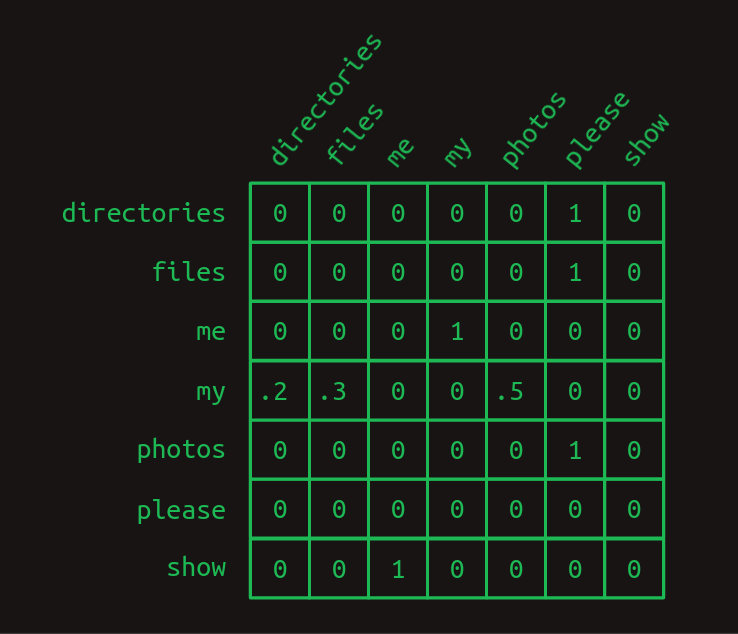
この遷移行列では、3つの文章の構造をはっきりと見ることができます。ほとんどすべての遷移確率は$0$または$1$です。マルコフ連鎖の中で、分岐が起こる場所は1つだけです。myの後に、directories、files、photosという単語が出てくるかもしれませんが、それぞれの確率は異なります。それ以外には、次にどの単語が来るかという不確かさはありません。この確かさは、遷移行列のほとんどが$1$と$0$であることに反映されています。

任意の単語に関連する遷移確率を取り出すために、one-hotベクトルとの行列の乗算を使うというトリックをもう一度考えてみます。例えば、myの後にどの単語が来るかの確率を特定したいだけなら、myという単語を表すone-hotベクトルを作り、それに遷移行列を掛けます。これにより、関連する行が取り出され、次の単語が何であるかの確率分布が示されます。

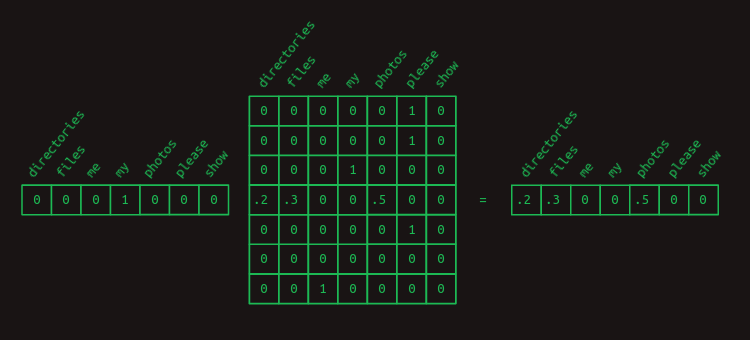
2次系列モデル

最も直近の単語だけから次の単語を予測するのは難しいです。最初の1音を聞いた後に、残りの部分の音楽を予想するようなものです。せめて2つの音を得られれば、可能性は大きく広がります。

これがどのように機能するかは、コンピュータコマンドの別のトイ言語モデルで理解することができます。このモデルでは、2つの文を$40/60$の割合でしか見ないことを期待します。

• Check whether the battery ran down please.
• Check whether the program ran please.

これの1次モデルとして、次のマルコフ連鎖があります。

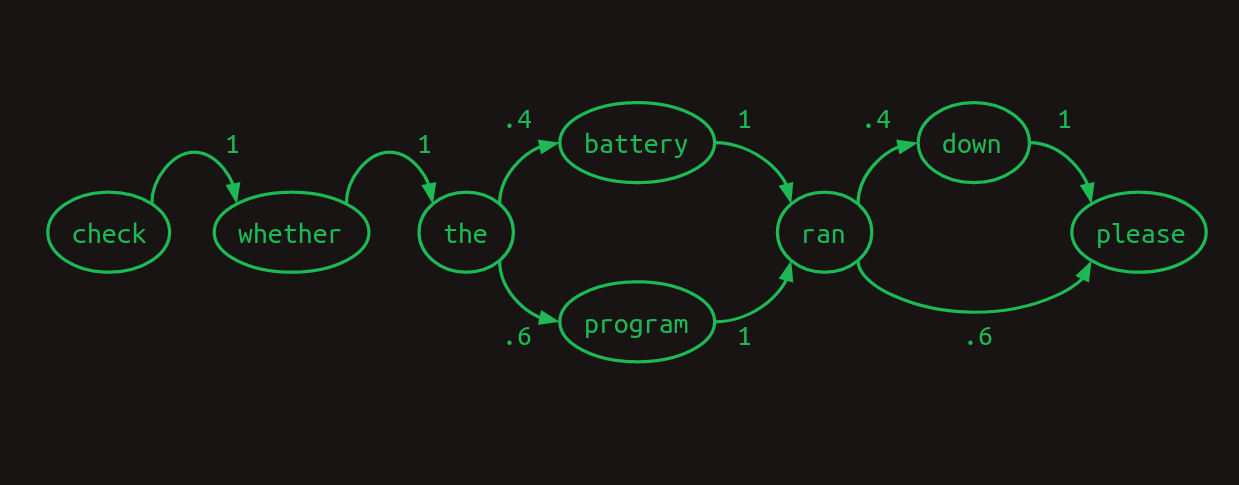
ここで、モデルが1つの単語だけでなく、最近の2つの単語を参照すれば、より良い結果が得られることが分かります。battery ranを見た時、次の単語はdownであることが分かり、program ranを見た時、次の単語はpleaseであることが分かります。これにより、モデル内の分岐の1つが無くなり、不確かさが減って信頼度が高まります。2つの単語を振り返るということは、これは2次マルコフモデルになります。これにより、次の単語の予測のベースとなる文脈が増えます。2次のマルコフ連鎖を描くのはより難しいのですが、ここではその値を示す接続を説明します。

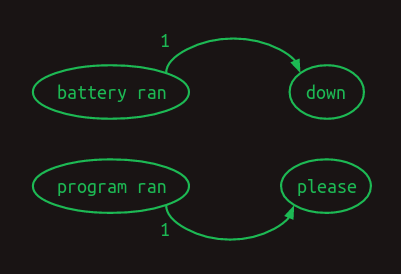
この2つの違いを強調するために、1次遷移行列を示します。

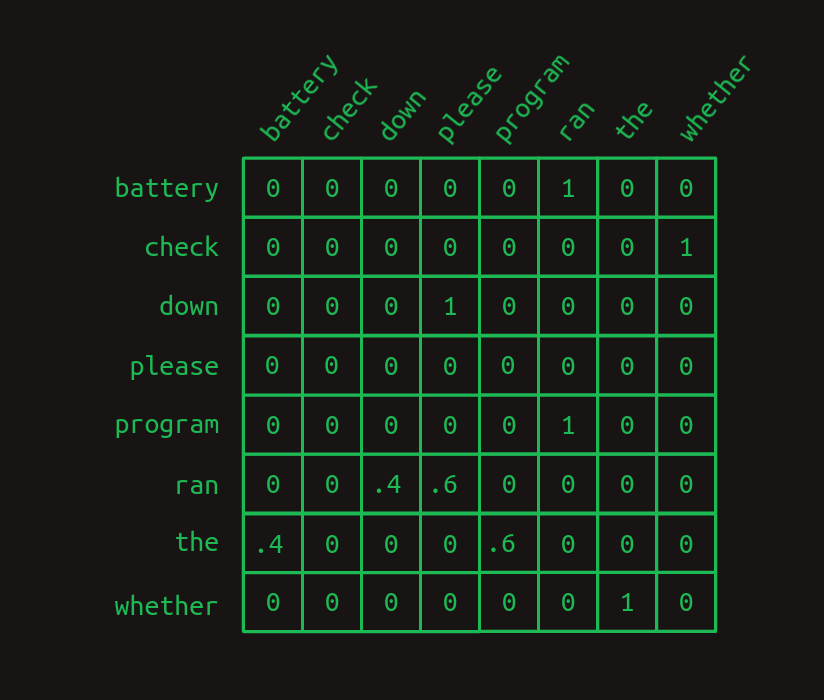
そして2次遷移行列を示します。

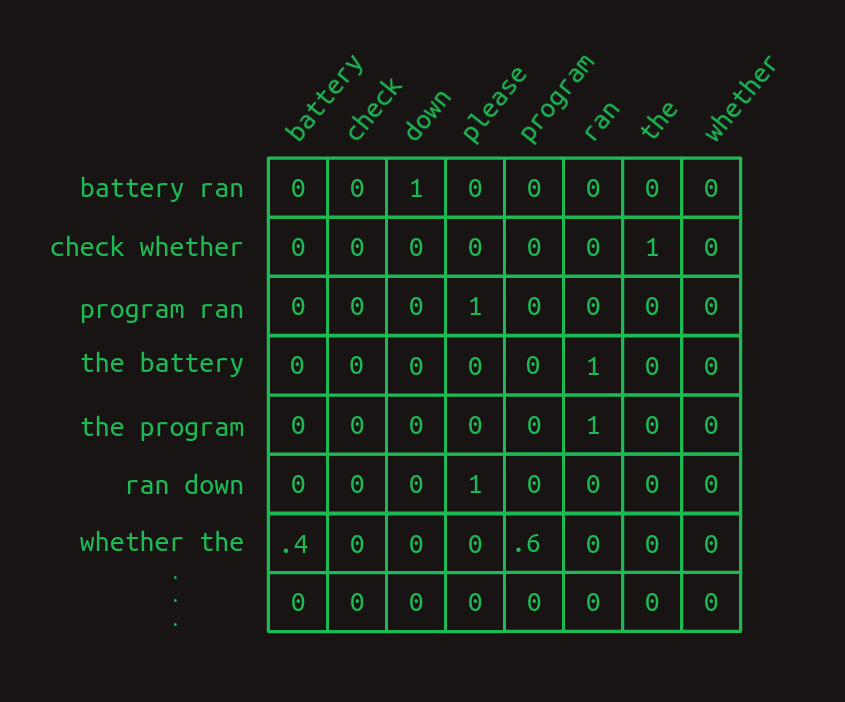
2次行列は、すべての単語の組み合わせ（ほとんどはここには示されていません）に対して別々の行を持っていることに注目してください。つまり、語彙の大きさが$N$の場合、遷移行列には$N^2$行あることになります。

これによってより大きな信頼度が得られます。2次モデルでは、$1$が多く、分数が少ないのです。私たちのモデルでは、分数が含まれる行は1つだけ、つまり1つの分岐だけです。直観的には、1つの単語ではなく2つの単語を見ることで、より多くの文脈、つまり次の単語を推測するためのより多くの情報を得ることができます。

スキップ付き2次系列モデル

2次モデルは、次の単語を決めるために2つの単語を振り返るだけでよい場合に有効です。しかし、もっと前を参照しなければならない場合はどうでしょうか。さらに別の言語モデルを構築している場合を想像してみましょう。このモデルでは、2つの文を表現するだけでよく、それぞれの文が等しい頻度で出現しそうです。

• Check the program log and find out whether it ran please.
• Check the battery log and find out whether it ran down please.

この例では、ranの後にどの単語が来るべきかを判断するために、過去の8つの単語を振り返る必要があります。2次言語モデルを改良したい場合、3次モデルや高次のモデルを考えることももちろんできます。しかし、かなりの語彙数がある場合、これを実行するには創造力と総当たりの組み合わせが必要になります。8次モデルを素朴に実装すると$N^8$行になり、まともな語彙数ではとんでもない行数になってしまいます。

その代わりに、2次モデルを作り、最も直近の単語とそれ以前の各単語の組み合わせを考慮するというずるい方法があります。一度に2つの単語しか考慮していないため、2次モデルであることに変わりはありませんが、さらにさかのぼって長期的な依存関係（long range dependencies） を取得することができます。この「スキップのある2次」と完全な13次モデルとの違いは、語順の情報と先行する単語の組み合わせのほとんどを捨ててしまうことです。残ったものはまだかなり強力です。

マルコフ連鎖は完全に失敗しましたが、先行する各単語のペアと後に続く単語の間のリンクを表現することはできます。ここでは、数値による重み付けはせずに、$0$ではない重みに関連する矢印のみを表示しています。大きな重みはより太い線で示されます。

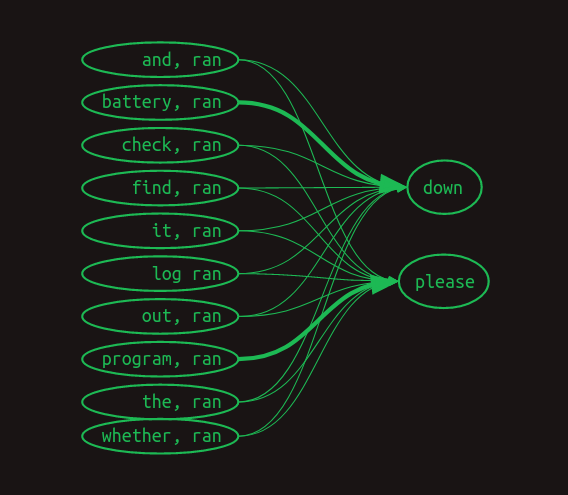
遷移行列では次のようになります。

この視点では、ranの後に来る単語の予測に関連する行のみが表示されます。最も直近の単語（ran）の前に、語彙中の他の各単語がある場合を示しています。関連する値のみが示されています。空のセルはすべて$0$です。

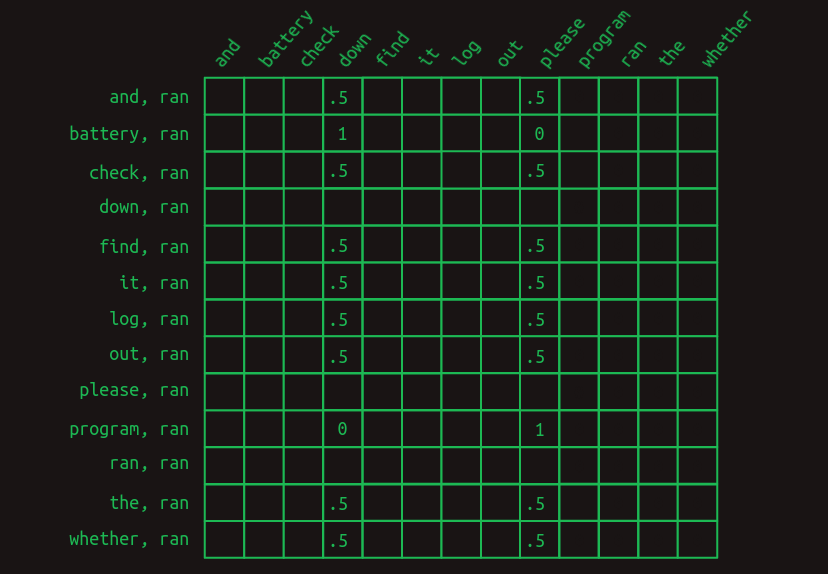
まずはっきりしてくることは、ranの後に続く単語を予測しようとすると、もはや1つの行ではなく、それら全体の集合を見ているということです。私たちは今、マルコフの世界から離れているのです。各行は、もはや特定の時点での配列の状態を表すものではありません。その代わり、それぞれの行は、特定の時点での系列を記述する可能性のある多くの特徴量（features） の1つを表しています。最も直近の単語とそれ以前のそれぞれの単語を組み合わせることで、適用可能な行の集まり、おそらく大きな集まりになります。このように意味が変わったため、行列のそれぞれの値はもはや確率ではなく、得票数を表しています。得票数は合計され、次の単語の予測を決めるために比較されます。

次にはっきりしてくることは、ほとんどの特徴量は重要ではないということです。ほとんどの単語は両方の文に出現するため、その単語が出現したからといって、次に来るものを予測するのには何の役にも立ちません。これらはすべて$0.5$の値を持っています。唯一の例外はbatteryとprogramです。これらには、$1$と$0$の重みが関連付けられています。battery, ranという特徴量は、ranが最も直近の単語で、batteryは文中のどこかで出現したことを示しています。この特徴量は、downに$1$の重みが、pleaseに$0$の重みが関連付けられています。同様に、program, ranという特徴量は、逆の重みを持っています。このような構造から、次に来る単語を予測するためには、文の前の方にこれら2つの単語があるかどうかが決め手だということがわかります。

この単語ペア特徴量の集合を次の単語の推定値に変換するには、関連するすべての行の値を合計する必要があります。列を足していくと、Check the program log and find out whether it ranという系列では、downを表す$4$、pleaseを表す$5$を除いて、すべての単語の合計が$0$になります。また、Check the battery log and find out whether it ranでも、downを表す$5$、pleaseを表す$4$を除いて、同じことを行います。得票数の多い単語を次の単語の予測として選ぶと、このモデルは8単語の深い依存関係があるにもかかわらず、正しい答えを得ることができます。

訳注

少し分かりにくいので、実際に計算してみた。

Check the program log and find out whether it ran に対応する計算:

$$4_{down} = 0.5_{and,\ ran}+0.5_{check,\ ran}+0.5_{find,\ ran}+0.5_{it,\ ran}+0.5_{log,\ ran}+0.5_{out,\ ran}+0_{program,\ ran}+0.5_{the,\ ran}+0.5_{whether,\ ran} \\ 5_{please} = 0.5_{and,\ ran}+0.5_{check,\ ran}+0.5_{find,\ ran}+0.5_{it,\ ran}+0.5_{log,\ ran}+0.5_{out,\ ran}+1_{program,\ ran}+0.5_{the,\ ran}+0.5_{whether,\ ran}$$

Check the battery log and find out whether it ran に対応する計算:

$$5_{down} = 0.5_{and,\ ran}+1_{battery,\ ran}+0.5_{check,\ ran}+0.5_{find,\ ran}+0.5_{it,\ ran}+0.5_{log,\ ran}+0.5_{out,\ ran}+0.5_{the,\ ran}+0.5_{whether,\ ran} \\ 4_{please} = 0.5_{and,\ ran}+0_{battery,\ ran}+0.5_{check,\ ran}+0.5_{find,\ ran}+0.5_{it,\ ran}+0.5_{log,\ ran}+0.5_{out,\ ran}+0.5_{the,\ ran}+0.5_{whether,\ ran}$$

マスキング

もっと慎重に考えると、これは満足のいくものではありません。4票と5票の差は比較的小さいのです。これは、モデルがそれほど自信を持っていないことを示唆しています。また、より大規模で自然な言語モデルでは、このようなわずかな違いが統計的なノイズに紛れてしまうことも容易に想像できます。

予測を鋭くするには、有益でない特徴量の得票数をすべて取り除く必要があります。battery, ranとprogram, ranを除いて。この時点で次のことを思い出すのが役に立つでしょう。遷移行列に今必要な特徴量を示すベクトルを掛けて、関連する行を取り出すということです。ここまでの例では、次のような暗黙の特徴量ベクトルを使ってきました。

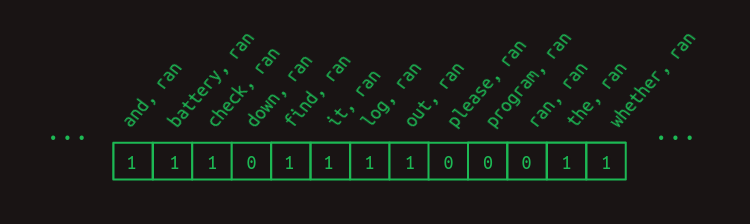
それには、それぞれの特徴量の1つを含み、この特徴量はranとその前に来るそれぞれの単語との組み合わせです。ranの後に来る単語は特徴量に含まれません（次の単語予測問題で、これらの単語はまだ見られていないことになります。そのため、それらを使って次の単語を予測するのは公平ではありません）。また、他のすべての取りうる単語の組み合わせも含まれていません。この例では、これらはすべて$0$になるので、無視しても問題ありません。

結果を改善するために、マスク（mask） を作ることで、役に立たない特徴量を強制的に$0$にすることができます。マスクとは、隠したり、マスクしたりしたい位置を除いた$1$のベクトルのことで、これらは$0$に設定されます。ここでは、battery, ranとprogram, ran以外のすべてをマスクしたいと思います。

マスクを適用するには、2つのベクトルを要素ごとに掛け合わせます。マスクされていない位置にある特徴量の値は$1$倍され、変わりません。マスクされた位置にある特徴量の様子（feature activity）の値は$0$が掛けられ、強制的に$0$になります。

マスクには、遷移行列の多くを隠す効果があります。batteryとprogramを除いたranとのすべての組み合わせを隠し、重要な特徴量だけを残します。

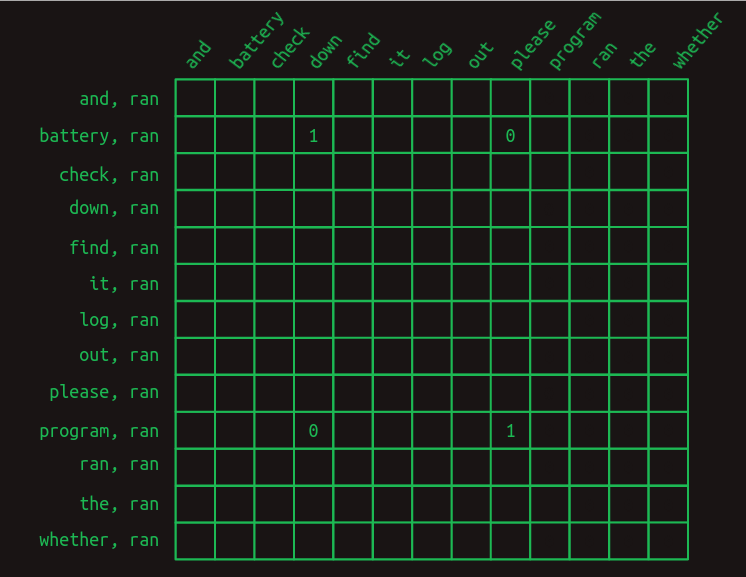
役に立たない特徴量をマスキングした後は、次の単語の予測が非常に強くなります。文中でbatteryという単語が先に出現した場合、ranの次の単語は、重みが$1$のdownと重みが$0$のpleaseと予測されます。25％の重みの違いが、無限大の違いになったのです。次にどの単語が来るかに疑いの余地はありません。programが早い段階で出現した場合、pleaseについても同様に強い予測が起こります。

この選択的なマスキングの過程が、Transformerの原著論文の題名にあるattentionなのです。ここまで説明してきたことは、論文の中でattentionがどのように実装されているかのおおよそにしか過ぎません。重要な概念は捉えていますが、詳細は異なります。この差は後で解消します。

休憩所と出口ランプ

ここまで来られて、おめでとうございます。必要に応じて中断できます。スキップ付き選択的2次（selective-second-order-with-skips）モデルは、少なくともデコーダ側で、Transformerが何をするのかについて考えるのに役立つ方法です。これは、OpenAIのGPT-3のような生成言語モデルが行っていることを、おおまかに捉えています。それは完全な筋書きではありませんが、それの核心を表しています。

次の節では、この直観的な説明と、Transformerがどのように実装されているかの間の差をより詳しく説明します。これらは主に、3つの実用上の考慮事項に基づいています。

1. コンピュータは行列の乗算を特に得意としています。 高速な行列演算のためのコンピュータのハードウェアを構築することで、業界全体が成り立っています。行列の乗算として表現できるあらゆる計算は、衝撃的なほど効率的です。弾丸列車のようなものです。荷物を乗せてしまえば、行きたいところに本当にすぐに行けるのです。
2. 各ステップは微分可能である必要があります。 これまではおもちゃの例を使っていたため、モデルのパラメータである遷移確率とマスク値をすべて手作業で選ぶという贅沢なことができました。実際には、これらのパラメータ（parameters） を誤差逆伝播法（backpropagation） によって学習する必要がありますが、これにはそれぞれの計算ステップが微分可能であることに依存しています。つまり、パラメータのわずかな変化に対して、モデルの誤差または損失（loss） に対応する変化を計算できることを意味します。
3. 勾配は滑らかで条件が整っている必要があります。 すべてのパラメータのすべての導関数の組み合わせが損失勾配です。実際に誤差逆伝播法をうまく動かすには、滑らかな勾配が必要です。つまり、どの方向に小さなステップを踏んでも、勾配がすぐに変化しないことです。また、勾配が適切に調整されている場合、つまり、ある方向と別の方向で急激に大きくならない場合にも、誤差逆伝播法は非常によく動きます。損失関数を風景に例えると、グランドキャニオンは条件の悪い風景と言えるでしょう。底辺に沿って移動するのか、側面に沿って移動するのかによって、移動する際の坂道が大きく異なります。対照的に、Windowsの古典的なスクリーンセーバーのなだらかな丘は、条件の良い勾配を持っているでしょう。
   ニューラルネットワークを構築する科学が、微分可能な構成要素を作ることだとすれば、ニューラルネットワークの技術は、勾配が急激に変化せず、どの方向でもほぼ同じ大きさになるようにピースを積み重ねることだと言えます。

行列の乗算としてのattention

特徴量の重みは、学習でそれぞれの単語ペア/次の単語の遷移が発生する頻度を数えることで簡単に構築できますが、attentionマスクはそうはいきません。ここまでは、何もないところからマスクベクトルを取り出してきました。Transformerがどのようにして関連するマスクを見つけるかが重要です。ある種のルックアップテーブルを使うのが自然でしょうが、今はすべてを行列の乗算で表現することに重点を置いています。上で紹介した探索方法と同じように、すべての単語のマスクベクトルを行列に積み重ね、最も直近の単語のone-hot表現を使って、関連するマスクを取り出すことができます。

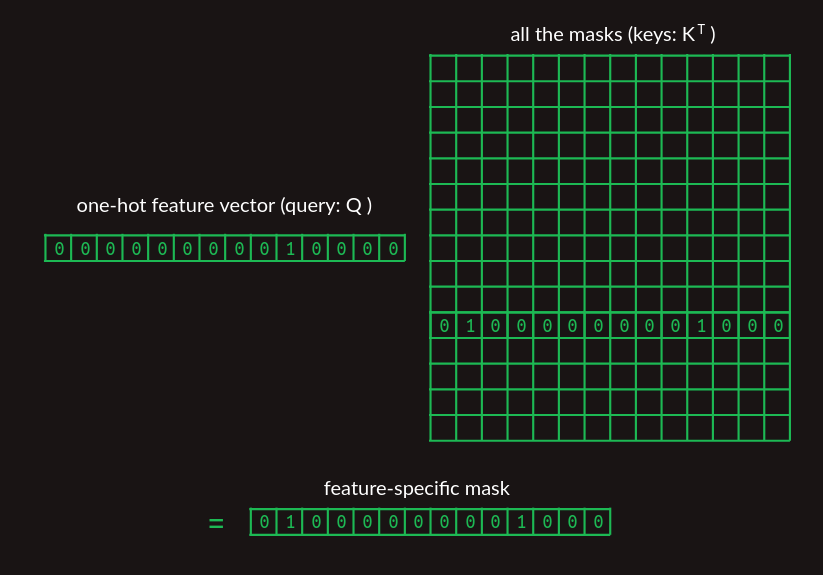
マスクベクトルの集まりを示す行列では、わかりやすくするために取り出そうとしているマスクベクトルのみを示しています。

ようやく論文に結びつけられるところまで来ました。このマスク探索は、attentionの式の$QK^T$項で表されます。

$$\rm{Attention}(\it{Q,K,V})=\rm{softmax}\left(\frac{\it{QK^T}}{\it{\sqrt{d_k}}}\right)\it{V}$$

クエリ$Q$は目的の特徴量を表し、行列Kはマスクの集まりを表しています。マスクが行ではなく列で格納されているため、乗算する前に（$T$演算子で）転置する必要があります。すべての作業が終わるまでには、これにいくつかの重要な修正を加えることになるでしょうが、このレベルでは、Transformerが利用する微分可能なルックアップテーブルの概念を捉えています。

行列の乗算としての2次系列モデル

これまで手探りで進めてきたもうひとつのステップが、遷移行列の構築です。論理的なことははっきりしていますが、行列の乗算をどのように行うかについてはそうではありませんでした。

attentionステップの結果、最も直近の単語とその前の単語の小さな集まりを含むベクトルが得られたら、これを、それぞれが単語ペアである特徴量に変換する必要があります。attentionマスキングは、必要な素材を得ることはできますが、単語ペアの特徴量を構築することはできません。そのためには、単層の全結合ニューラルネットワークを使うことができます。

ニューラルネットワークの層がどのようにしてこれらのペアを作るかを見るために、私たちは手作業でペアを作ってみます。人工的にきれいに様式化され、その重みは実際の重みとは似ても似つかないものになりますが、ニューラルネットワークがこれらの2つの単語ペアの特徴量を構築するのに必要な表現力を持っていることを示します。小さくすっきりさせるために、この例から登場した3つの単語、battery、program、ranだけに焦点を当てます。

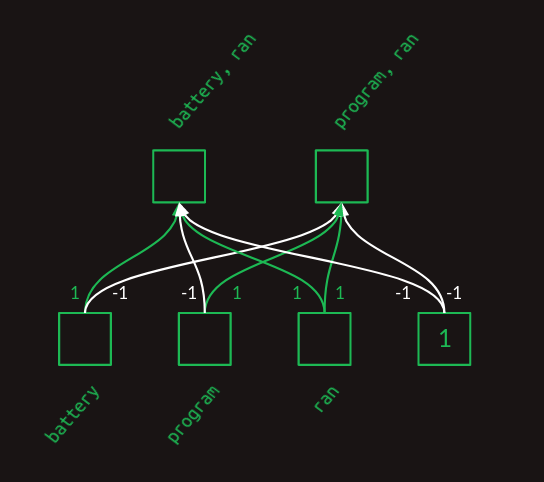
上の層の図では、重みがどのように作用して、それぞれの単語の有無を組み合わせて特徴量の集まりにするのかがわかります。これは行列形式でも表現できます。

そしてそれは、これまでに見た単語の集まりを表すベクトルとの行列の乗算によって算出することができます。

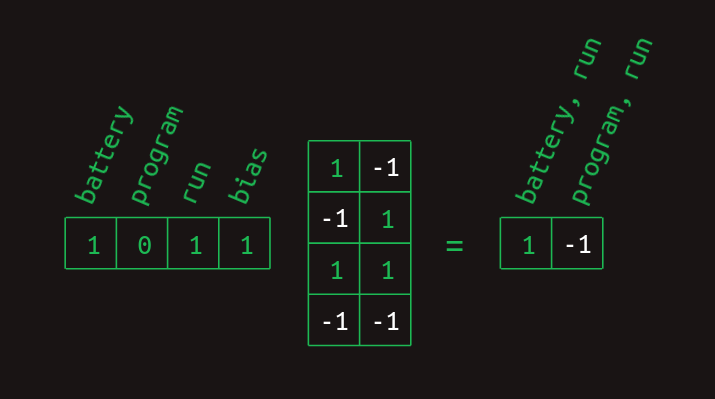
これらの単語組み合わせの特徴量を計算する最後のステップは、正規化線形ユニット（ReLU）の非線形性の適用です。この結果、負の値を$0$に置き換えられます。これにより、これらの結果は、それぞれの単語組み合わせの特徴量が存在するか（$1$）または、存在しないか（$0$）を表すように整理されます。

このような工夫を経て、ようやく行列の掛け算に基づく複数単語の特徴量を作成する方法ができました。当初、最も直近の単語とそれ以前の単語から構成されると主張しましたが、この方法をよく見てみると、他の特徴も構築できることがわかります。ハードコーディングするのではなく、特徴量生成行列を学習させると、他の構造を学習させることができます。このおもちゃの例でも、battery, program, ranのような3単語の組み合わせが作られるのを妨げるものは何もありません。もし、このような組み合わせが一般的ならば、おそらくその組み合わせが表現されることになるでしょう。どのような順番で単語が出現したかを示す方法はありませんが（少なくとも今は）、その共起性を使って予測することは当然できます。batteryやprogramのように、直近の単語を無視した単語の組み合わせも考えられるでしょう。このようなタイプの特徴量は、おそらく実際に生成されるものであり、Transformerが選択的2次配列モデルであると主張したときに私が行った過度の単純化をさらけ出したものです。それ以上の意味合いを持つものであり、その意味合いが何であるかがよくお分かり頂けたと思います。より微妙な表現を取り入れるために話を変更するのは、これが最後ではありません。

この形で、マルチワード特徴量行列は、もう一つの行列の乗算、つまり、上で開発したスキップ付き2次系列モデルの準備が整ったことになります。すべて合わせた、

• 特徴量生成行列の乗算
• ReLUの非線形性
• 遷移行列の乗算

の一連の処理は、attentionが適用された後に適用される順伝播処理の段階です。論文にある式2は、これらの段階を簡潔な数学的定式化で示したものです。

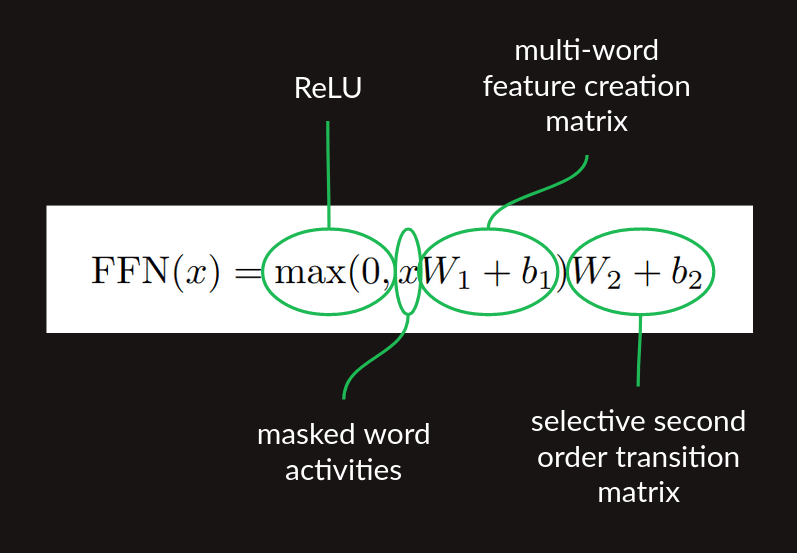
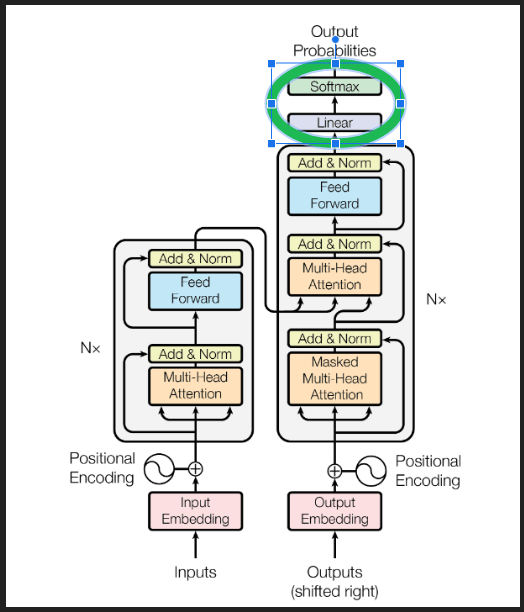
論文の図1のアーキテクチャ図では、これらを一括して Feed Forward ブロックとして示しています。

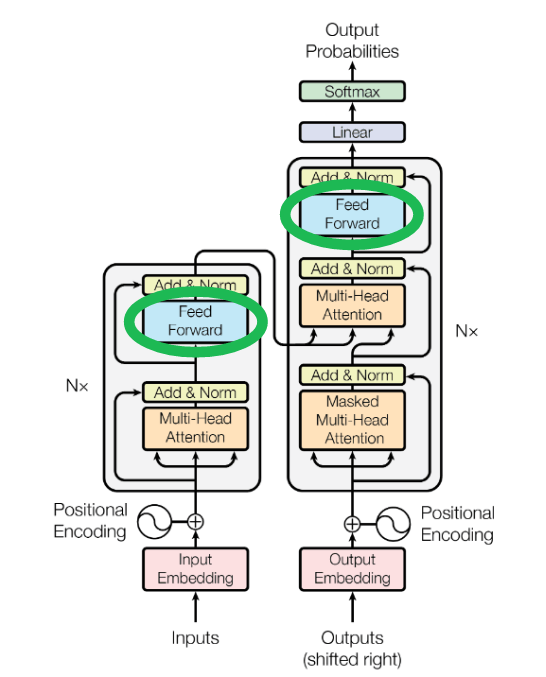
系列補完

ここまでは、次の単語予測についてだけ説明しました。デコーダが長い系列を生成するためには、いくつかの部品を追加する必要があります。1つ目はプロンプト（prompt） で、Transformerに実行の開始と系列の残りの部分を構築するためのコンテキストを提供するための例示的なテキストです。これはデコーダーに入力され、上の画像の右側の列にある「Outputs (shifted right)」というラベルが貼られます。関心のある系列を生成するプロンプトを選択することは、それ自体が一芸であり、プロンプトエンジニアリングと呼ばれています。これはまた、アルゴリズムが人間を支援するためにアルゴリズム自身の行動を修正するより、むしろその逆を行っている優れた例です。

いったんデコーダが開始するための部分的な系列を得ると、デコーダは順方向処理を行います。最終的な結果は、予測される単語の確率分布の集合であり、系列内の各位置に1つの確率分布が存在することになります。それぞれの位置で、確率分布は語彙の中の次のそれぞれの単語の予測確率を示しています。私たちは、単語列の中で確定されたそれぞれの単語の予測確率には関心がありません。それらはすでに確定しています。私たちが本当に関心があるのは、プロンプトの終わりの次の単語に対する予測確率です。その単語を選ぶにはいくつかの方法がありますが、最も素朴な方法は貪欲（greedy） と呼ばれるもので、最も高い確率を持つ単語を選択することです。

そして、新しい次の単語が系列に追加され、デコーダの下部にある「Outputs」で代入され、このプロセスが飽きるほど繰り返されます。

まだ詳しく説明していない部分がありますが、これもマスキングの一種で、Transformerが予測を行う際に、前方ではなく後方だけを見るようにするためのものです。これは「Masked Multi-Head Attention」と呼ばれるブロックに適用されています。これは後ほど、どのように行われるのかを明確にした上で、もう一度考えてみたいと思います。

埋め込み

これまで説明してきたように、Transformerはあまりにも巨大です。語彙数Nが仮に5万だとすると、単語のすべてのペアとすべての次の単語候補の間の遷移行列は、5万の列と5万の2乗（25億）行、合計100兆以上の要素を持つことになります。これは現代のハードウェアでもまだ不可能なことです。

問題なのは行列の大きさだけではありません。安定した遷移言語モデルを構築するためには、少なくとも数回は、すべての想定される系列を表現した学習データを用意しなければなりません。これでは、どんなに優れた学習データセットでも、その処理能力をはるかに超えてしまいます。

幸いなことに、この2つの問題を回避する方法があります。

言語のOne-Hot表現では、各単語に対して1つのベクトル要素があります。大きさがNの語彙の場合、そのベクトルはN次元の空間となります。それぞれの単語は、その空間において、原点から1単位離れた軸のいずれかに沿った点を表します。高次元空間を描く良い方法はまだ見つかっていませんが、以下に粗い表現で示しておきます。

埋め込みでは、これらの単語点がすべて取り出され、低次元空間に再構成（線形代数における射影（projected））されます。上の図は、例えば2次元空間での様子を示しています。ここで、単語を特定するのに必要な数値はNではなく、2だけです。これらは、新しい空間における各点の(x, y)座標です。以下は、このおもちゃの例の2次元埋め込みがどのように見えるか、いくつかの単語の座標と合わせて示したものです。

良い埋め込みは、似たような意味を持つ単語をひとまとめにします。埋め込みを利用するモデルは、埋め込まれた空間におけるパターンを学習します。すなわち、ある単語を学習すると、その単語のすぐ隣にあるすべての単語に自動的にその学習が適用されるのです。これは、必要な学習データの量を減らすという効果もあります。それぞれの例が、周辺の単語全体に渡って適用される少量の学習をもたらすのです。

この図では、重要な構成要素（battery, log, program）をある場所に、前置詞（down, out）を別の場所に、動詞（check, find, ran）を中心付近に置くことでそれを示そうとしたのです。実際の埋め込みでは、グループ分けはそれほどはっきりしないし、また直観的でもないかもしれませんが、根底にある概念は同じなのです。同じような振る舞いをする単語間の距離は小さくなります。

埋め込みを行うと、必要なパラメータの数を圧倒的に減らすことができます。しかし、埋め込み空間の次元が小さくなればなるほど、元の単語に関する情報が捨てられてしまいます。言語の豊かさには、重要な概念をすべて敷き詰め、互いに踏み込まないようにするために、やはりかなりの空間が必要なのです。埋め込み空間のサイズを選択することで、計算負荷とモデルの精度を両立させることができるのです。

単語をone-hot表現から埋め込み空間に射影するには、行列の乗算が必要であることは、おそらくそれほど驚くことではないでしょう。射影は行列が最も得意とするところです。1行N列のone-hot行列から始めて、2次元の埋め込み空間に進むと、射影行列はここに示すようにN行2列となります。

この例では、例えばbatteryを表すone-hotベクトルが、それに関連する行を取り出し、それが埋め込み空間における単語の座標を含んでいる様子を示しています。この関係をより明確にするために、one-hotベクトルの0は、射影行列から取り出されない他のすべての行と同様に、隠されています。完全な射影行列は密であり、それぞれの行は関連する単語の座標を含んでいます。

射影行列は、元のone-hot語彙ベクトルの集合を、任意の次元の空間における任意の構成に変換することができます。最大のトリックは、類似の単語がグループ化され、それらを拡張するのに十分な次元を持つ、有用な射影を見つけることです。英語のような一般的な言語には、あらかじめ計算された適切な埋め込みがいくつか存在します。また、Transformerの他のすべてのものと同様に、訓練中に学習することができます。

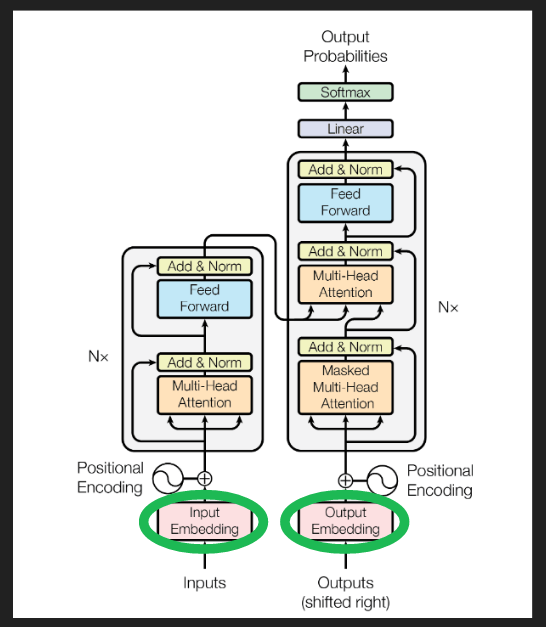
原著論文の図1のアーキテクチャ図において、埋め込みが行われる場所は以下の通りです。

位置エンコーディング

これまで、少なくとも最も直近の単語より前に来る単語については、単語の位置は無視されると仮定してきました。ここで、位置情報を埋め込むことによって、それを修正します。

単語の埋め込み表現に位置情報を導入する方法はいくつかありますが、当初のTransformerでは、円弧状のくねりを追加する方法でした。

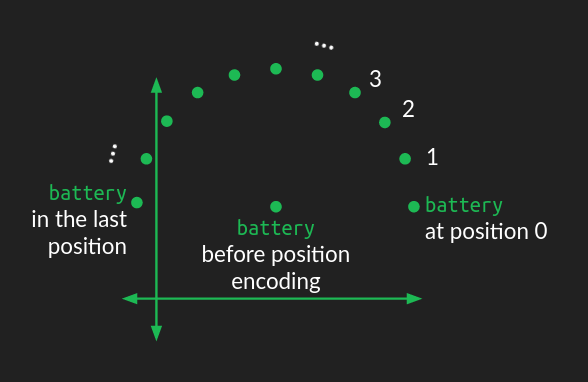
埋め込み空間における単語の位置は、円の中心のように作用します。そこに、単語の系列の順序のどこに位置するかに応じて、摂動が加えられます。それぞれの位置に対して、単語は同じ距離ですが異なる角度で移動され、結果として系列を通過するにつれて円形のパターンになります。系列内で互いに近い位置にある単語は同様の摂動を受け、遠い位置にある単語は異なる方向に摂動が加えられます。

円は2次元の図であるから、円形のくねりを表現するためには、埋め込み空間の2次元を修正する必要があります。埋め込み空間が2次元以上から成り立つ場合（ほとんどの場合そうですが）、円形くねりは他のすべての次元の組で繰り返されますが、角度の頻度が異なります、つまり、それぞれの場合で異なる回転数を掃引することになります。ある次元の組では、くねりが円の多くの回転を掃引します。また、他の次元の組では、ほんのわずかな回転数しか掃引しません。これらの異なる周波数の円形のくねりの組み合わせにより、系列内の単語の絶対位置が表現されます。

なぜこれが有効なのかについては、まだ直観的な理解を深めているところです。単語とattentionの間の学習された関係を壊さない方法で、位置情報をミックスして追加しているようです。数学とその意味についてより深く掘り下げるには、Amirhossein Kazemnejadによる位置エンコーディングのチュートリアルをお勧めします。

典型的なアーキテクチャ図では、これらのブロックは位置符号の生成と埋め込まれた単語への付加を示しています。

脱埋め込み（De-embeddings）

単語を埋め込むと処理効率が格段に上がりますが、パーティーが終わったら、元の語彙の単語に戻す必要があります。脱埋め込みは埋め込みと同じように行われ、ある空間から別の空間への射影、つまり行列の掛け算で行われます。

脱埋め込み行列は埋め込み行列と同じ形状ですが、行と列の数が反転しています。行の数は、変換元の空間の次元数です。これまでの例では、埋め込み空間のサイズの2です。列の数は変換先の空間の次元数で、完全な語彙のone-hot表現のサイズであり、この例では13です。

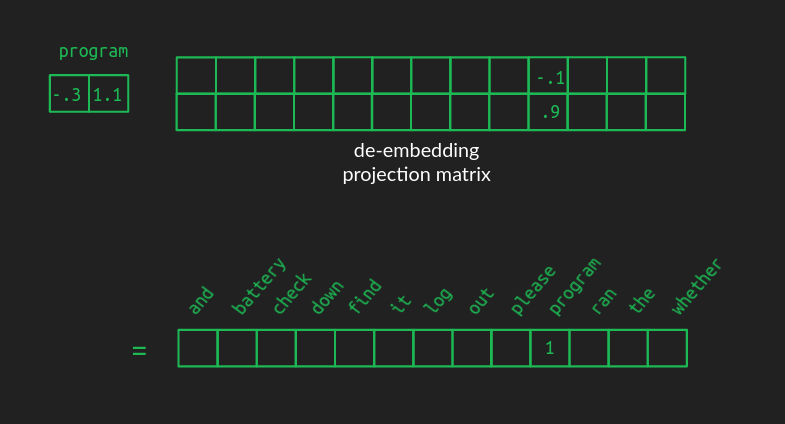
優れた脱埋め込み行列の値は、埋め込み行列の値ほど簡単には説明できませんが、その効果は似ています。例えば、programという単語を表す埋め込みベクトルに脱埋め込み行列を掛けると、対応する位置の値は大きくなります。しかし、高次元空間への射影の仕組みから、他の単語に関連する値は0にはなりません。埋め込み空間でprogramに最も近い単語は、中～高程度の値も持つことになります。それ以外の単語は、ほぼ0に近い値になります。そして、負の値を持つ単語も多くなることが考えられます。語彙空間の出力ベクトルは、もはやone-hotでも疎でもありません。ほぼすべての値が0でない、密なものになるでしょう。

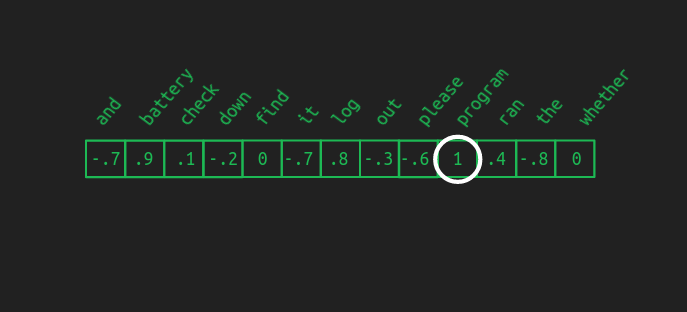
これでOKです。最大値に関連する単語を選ぶことで、one-hotベクトルを作り直すことができます。この操作は、最大値を与える引数（要素）のことで、argmaxとも呼ばれます。これが前述した、貪欲な系列補完の方法です。最初の一歩としては上出来ですが、もっといい方法があります。

ある埋め込みが複数の単語にとてもうまく対応する場合、毎回最も良いものを選択したいとは思わないでしょう。他のものよりもほんの少し良い選択かもしれませんし、多様性を持たせることで、結果をより興味深いものにすることができます。また、最終的な選択をする前に、数単語先を見て、文が進む方向をすべて検討することが有効な場合もあります。これらを行うには、まず、脱埋め込みした結果を確率分布に変換する必要があります。

Softmax

argmax関数は、たとえ他の値よりも無限大に大きい値であったとしても、最も高い値が勝つという意味で「ハード」です。一度に複数の可能性を考慮したい場合は、softmaxで得られるような「ソフトな」最大化関数がよいでしょう。ベクトル中の値xのsoftmaxを求めるには、xのべき乗、$e^x$をベクトル中のすべての値のべき乗の和で割れば良いのです。

softmaxは、3つの理由で役に立ちます。まず、脱埋め込み結果のベクトルを任意の値の集合から確率分布に変換してくれます。確率として、異なる単語が選択される尤度を比較することが容易になり、さらに将来を見据えた場合、複数の単語の系列の尤度を比較することも可能になるのです。

次に、上位の単語をより絞り込むことができます。ある単語が他の単語より明らかに高いスコアを出した場合、softmaxはその差を強調し、ほとんどargmaxのように、勝者の値が1に近く、他のすべてが0に近くなるように見せます。しかし、複数の単語がすべて上位に近い結果になった場合、2位の結果を人為的につぶすのではなく、それらをすべて高い確率として保存します。

3つ目は、softmaxは微分可能であることです。つまり、入力要素のいずれかが少し変化したときに、結果のそれぞれの要素がどのくらい変化するかを計算することができるのです。このため、バックプロパゲーションと組み合わせて、Transformerを学習させることができます。

softmaxの理解を深めたい方（あるいは夜なかなか眠れなくなってしまった方）は、こちらの記事でより詳しく解説しています。

脱埋め込み変換（下図の線形ブロック）とsoftmax関数を組み合わせることで、脱埋め込み処理が完了します。

Multi-head attention

射影（行列の乗算）と空間（ベクトルの大きさ）の概念と和解した今、私たちは新たな気持ちで核心のattention機構を見直すことにします。それぞれの段階での行列の形状をより具体的に示すことができれば、アルゴリズムを明確にすることができるでしょう。そのために重要な値がいくつか挙げられます。

N: 語彙の大きさ。この例では13。通常、数万単位。
n: 最大配列長。この例では12。論文では数百程度。（具体的には書かれていない。）GPT-3では2048。
d_model: モデル全体で用いられる埋め込み空間の次元数。論文では512。

元の入力行列は、文中のそれぞれの単語をone-hot表現で取り出し、それぞれのone-hotベクトルがそれ自身の行となるように積み重ねることで構成されます。結果として得られる入力行列はn行N列となり、これを[n x N]と略記することができます。

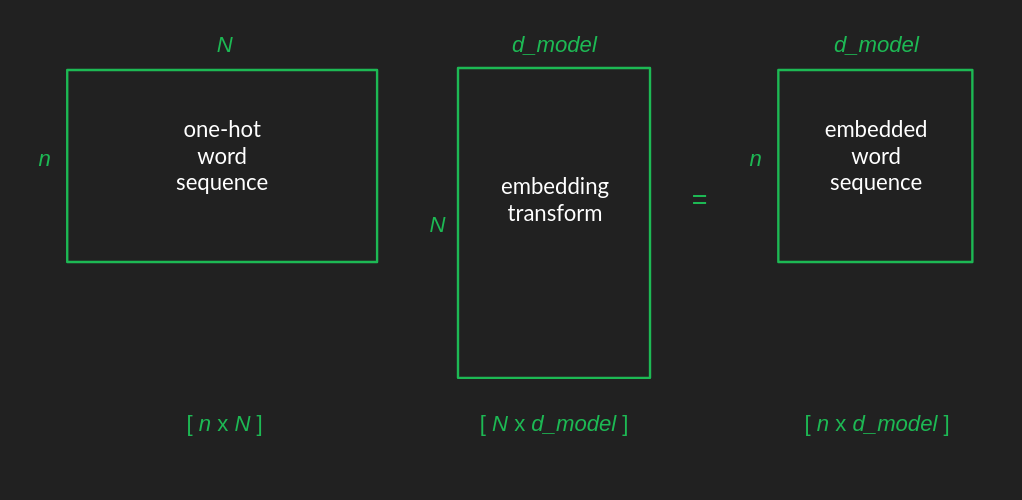
先に説明したように、埋め込み行列はN行、d_model列で、[N x d_model]と略記することができます。2つの行列を乗算する場合、その結果は、最初の行列から行の数を、2番目の行列から列の数を得ます。これにより、埋め込まれた単語列の行列は[N x d_model]という形状になります。

Transformerを通して行列の形状の変化を追いかけることで、何が起こっているかを把握することができます。最初の埋め込みの後、位置エンコーディングは乗算ではなく加算なので、形状は変わりません。そして、埋め込まれた単語列は、attention層に入力され、同じ形で反対側から出力されます。（これらの内部構造については後述します。）最後に、脱埋め込みによって行列は元の形状に復元され、語彙のすべての単語に対する確率が系列のすべての位置で得られることになります。

なぜ複数のattentionヘッドが必要なのか

ようやく、attention機構を説明する最初の段階で私が行った単純化された仮定のいくつかに直面するときが来ました。単語はone-hotベクトルではなく、密な埋め込みベクトルとして表現されます。attentionは1か0か、オンかオフかだけでなく、その中間の値も取り得ます。0と1の間に入るようにするために、再びsoftmaxのトリックを使用します。これは、すべての値が[0, 1]のattentionの範囲にあることを強制し、最大の値を強調し、最小の値を積極的に押しつぶすという2つの利点があります。これは以前、モデルの最終出力を解釈するときに利用した、微分の近似的なargmaxの挙動です。

softmax関数をattentionに導入したことによる複雑な結果には、1つの要素に焦点を当てる傾向があります。これは以前にはなかった制限です。次の単語を予測するときに、直前の単語をいくつか記憶しておくと便利なことがありますが、softmaxはそれを奪ってしまったのです。これはこのモデルの問題点です。

解決策は、複数の異なるattentionのインスタンス、またはヘッドを同時に実行させることです。これにより、Transformerは次の単語を予測する際に、同時にいくつかの前の単語を考慮することができます。これは、softmaxを導入する前に持っていた力を取り戻すことになります。

しかし、残念ながら、この方法は計算負荷を増大させます。attentionの計算がすでに作業の大部分を占めており、それに使用するヘッドの数を掛けただけなのです。これを回避するには、低次元の埋め込み空間にすべてを射影するというトリックを再利用すればよいのです。これによって、関係する行列が縮小され、計算時間が劇的に短縮されます。これで一安心です。

このことがどのように実現されるかを見るために、行列の形状を観察し続けてみましょう。multi-head attentionブロックの分岐や織り込みを通して行列の形状を辿るには、あと3つの数値が必要です。

d_k: キーとクエリに使用される埋め込み空間の次元。論文中では64。
d_v: 値に用いられる埋め込み空間の次元。論文中では64。
h: ヘッドの数。論文では8。

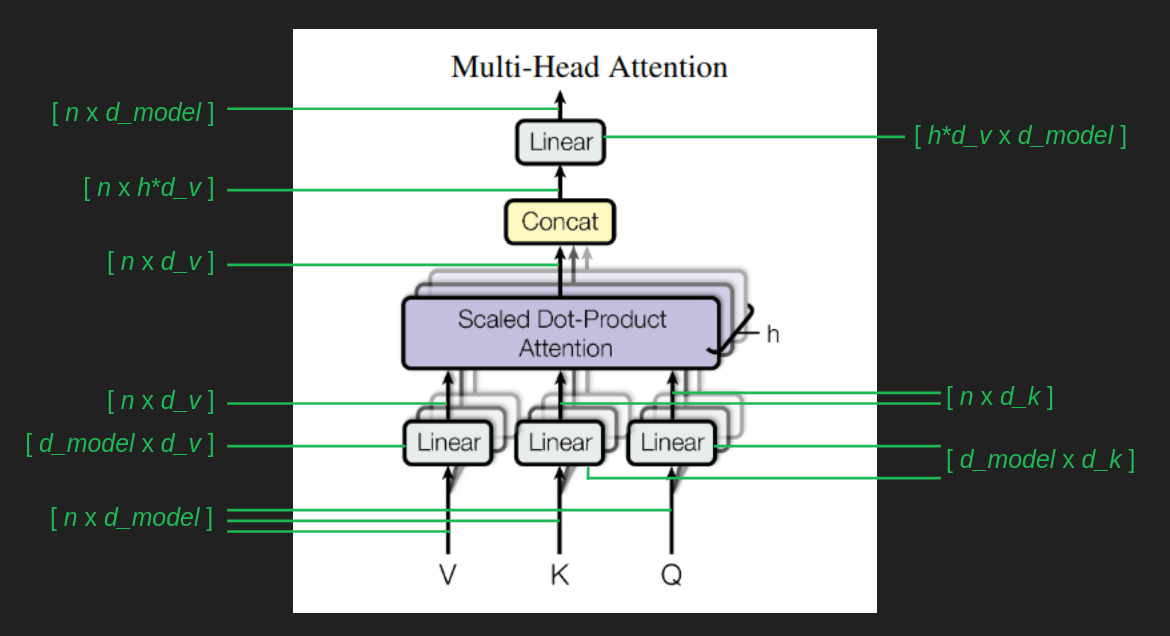
埋め込み単語列[n x d_model]は、この後に続くすべてのものの基礎となるものです。それぞれの場合において、行列$W_v$、$W_q$、$W_k$（アーキテクチャ図ではすべて「線形」ブロックとして不親切に示されています）があり、元の埋め込み単語列を値行列V、クエリー行列Q、キー行列Kに変換しています。論文ではd_kとd_vが同じであることが少し混乱を招いていますが、そうである必要はありません。この設定の重要な点は、それぞれのattentionヘッドが独自の$W_v$、$W_q$、$W_k$変換を持つことです。つまり、各ヘッドは埋め込み空間の中で自分が注目したい部分を拡大・縮小することができ、それらは他の各ヘッドが注目している部分と異なっていても構わないということです。

それぞれのattentionヘッドの結果はVと同じ形状をしています。ここで、h個の異なる結果ベクトルがあるという問題が発生し、それぞれのベクトルは系列の異なる要素に着目しています。これらを1つにまとめるには、線形代数の力を借りて、これらの結果を1つの巨大な[n x h * d_v]行列に連結すればよいのです。そして、最終的に同じ形状になるように、[h * d_v x d_model]という形状の変換をもう1つ行います。

以下は、そのすべてを簡潔に述べたものです。

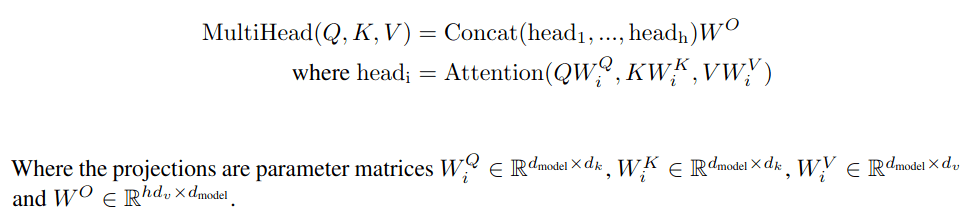
Single head attention再訪

私たちはすでに、上記のattentionの概念的な図解を歩んできました。実際の実装はもう少し厄介ですが、先ほどの直観はまだ役に立ちます。クエリーとキーはそれぞれ固有の部分空間に射影されるため、もはや調べたり解釈したりするのは簡単ではありません。この概念図では、クエリ行列の1行は語彙空間の1点を表し、これはone-hot表現のおかげで、1つだけの単語を表します。埋め込まれた形では、クエリ行列の1行は埋め込み空間の1点を表し、それは類似した意味と用法を持つ単語群の近くに位置することになります。概念図では、1つのクエリ単語をキーの集合にマッピングし、その結果、注目されていないすべての値をフィルタリングしています。実際の実装では、各attentionヘッドは、クエリー単語をさらに別のより低次元の埋め込み空間内の点にマッピングします。この結果、attentionは個々の単語間ではなく、むしろ単語グループ間の関係となります。意味的な類似性（埋め込み空間における近さ）を利用して、類似した単語について学習したことを一般化するのです。

attentionの計算を通して行列の形状をたどることは、それが何を行っているかを追跡するのに役立ちます。

クエリー行列とキー行列であるQとKはどちらも[n x d_k]の形状をしています。Kは乗算の前に転置されるため、Q K^T の結果は [n x d_k] * [d_k x n] = [n x n] という行列になります。この行列のそれぞれの要素をd_kの平方根で割ることで、値の大きさが乱高下せず、誤差逆伝播法がうまく機能することが分かっています。softmaxは、前述のように、結果をargmaxの近似に縮めるもので、系列の1つの要素に他の要素よりも焦点を当てる傾向があります。この形式では、[n x n]のattention行列は系列のそれぞれの要素を系列の他の要素に大まかに対応付け、次の要素を予測するために最も関連したコンテキストを得るために何を見るべきかを示しています。これは最終的に値行列Vに適用されるフィルターであり、注目された値の集合だけを残します。これは、系列内の前の要素の大部分を無視し、注意すべき最も有用な1つの前の要素にスポットライトを当てるという効果があります。

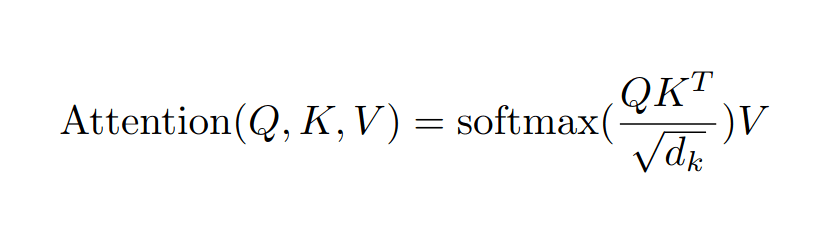
この一連の計算を理解する上で厄介なのは、入力系列のそれぞれの要素、つまり最も直近の単語だけでなく、文中のそれぞれの単語に対してattentionを計算していることを留意しておくことです。また、それ以前の単語に対するattentionも計算されています。私たちはこれらの単語については、次の単語がすでに予測され確立されているため、あまり気にしません。また、未来の単語に対するattentionも計算されています。これらはあまりにも先のことであり、直前の単語がまだ選択されていないため、まだあまり意味がありません。しかし、これらの計算が最も直近の単語に対するattentionをもたらす間接的な経路があるため、それらをすべて含めています。ただ、最後の方になって系列のそれぞれの位置の単語確率を計算すると、そのほとんどを捨てて次の単語にだけ注意を払う（pay attention）ことになるだけです。

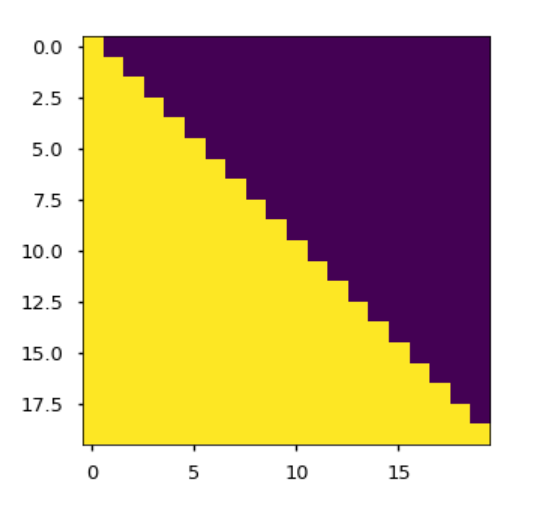
Maskブロックは、少なくともこの系列補完タスクにおいては、未来を覗くことはできないという制約を課しています。これにより、未来の架空の単語から奇妙なアーティファクトが発生するのを防ぐことができます。手作業で現在位置より過去のすべての単語に適用するattentionを負の無限大に設定するという、粗雑かつ効果的な方法です。Pythonの実装を1行ずつ紹介した論文の計り知れないほど役立つ仲間であるThe Annotated Transformerでは、マスク行列が視覚化されています。紫色のセルは、attentionが無効となる箇所を示しています。それぞれの行は系列の要素に対応します。最初の行はそれ自身（最初の要素）にはattentionが適用されますが、それ以降には何も適用されません。最後の行はそれ自身（最後の要素）とその前に来るもの全てにattentionが許されます。Maskブロックは[n x n]の行列であり、行列の乗算ではなく、より単純な要素ごとの積で適用されます。これは、手作業でattention行列に入り、Maskブロックのすべての紫の要素を負の無限大に設定する効果があります。

attentionがどのように実装されているかにおけるもう一つの重要な違いは、系列中の単語が提示される順序を利用し、attentionを単語対単語の関係ではなく、位置対位置の関係として表現している点です。このことは、その[n x n]の形状に現れています。行のインデックスで示される系列からのそれぞれの要素を、列のインデックスで示される系列の他の要素に対応させます。これは、埋め込み空間上で処理されているため、何をやっているのか、より簡単に視覚化し解釈することができます。クエリーとキーの関係を表現するために、埋め込み空間で近くの単語を見つけるという余分なステップを省くことができます。

スキップ接続

attentionは、transformerが行うことの最も基本的な部分です。核となる仕組みで、ここまででかなり具体的なレベルまで踏み込んできました。ここから先は、それをうまく機能させるために必要な仕組みです。私たちの重い仕事を引っ張ってくれるのは、残りの部分であるハーネスなのです。

まだ説明していないのが、スキップ接続です。これは、Multi-Head Attentionブロックの周辺と、Add and Normと書かれたブロックの中のElement wise Feed Forwardブロックの周辺に現れます。スキップ接続では、一連の計算の出力に入力のコピーが追加されます。attentionブロックへの入力は、その出力に追加し直されます。要素ごとの順伝播（the element-wise feed forward）ブロックへの入力は、その出力に追加されます。

スキップ接続には2つの目的があります。

1つ目は、勾配を滑らかに保つことで、逆伝播法の大きな助けとなることです。attentionはフィルターであり、正しく機能しているときは、それを通過しようとするもののほとんどを遮断することを意味します。その結果、多くの入力におけるわずかな変化が、遮断されたチャンネルにたまたま入った場合、出力に大きな変化をもたらさないことがあります。これにより、勾配が平坦であっても、谷底に近くない場所に死角が生じます。このような鞍点や尾根は、逆伝播法では大きな障害になります。スキップ接続はこれらを滑らかにするのに効果的です。attentionの場合、すべての重みがゼロですべての入力が遮断されたとしても、スキップ接続は入力のコピーを結果に追加し、入力のどれかにわずかな変化があっても結果に顕著な変化をもたらすことを保証します。これにより、勾配降下法が適切な解から遠く離れたところで行き詰まるのを防ぐことができます。

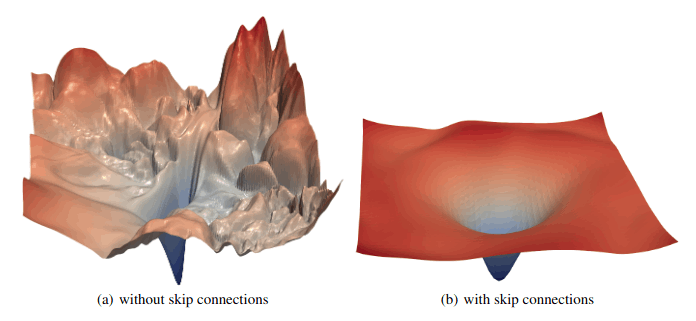
スキップ接続は、ResNet画像分類器の時代から、それらがいかに性能を向上させてきたかということで人気を博してきました。今ではニューラルネットワークアーキテクチャの標準的な特徴となっています。視覚的にも、スキップ接続のあるネットワークとないネットワークを比較することで、スキップ接続の効果を確認することができます。下の図は、ResNetにスキップ接続がある場合とない場合を示しています。損失関数の丘の傾斜は、スキップ接続を使用した場合の方がより緩やかで均一です。もし、スキップ接続がどのように機能し、なぜ機能するのかをもっと深く知りたければ、この投稿でより深く説明しています。

スキップ接続の2つ目の目的は、transformerに特有のもので、元の入力系列を保持することです。多くのattentionヘッドがあっても、ある単語が自分の位置に注目する保証はありません。attentionフィルタが最も直近の単語を完全に忘れてしまい、関連性のありそうな以前の単語を全て見てしまうこともあり得るのです。スキップ接続は、元の単語を取り出し、それを手動で信号に戻すため、単語を見逃したり忘れたりすることはありません。このような頑健性が、transformerが様々な系列補完タスクで優れた挙動を示す理由の一つなのかもしれません。

層の正規化

正規化はスキップ接続と相性の良いステップです。必ずしも一緒にしなければならない理由はありませんが、attentionや順伝播ニューラルネットワークのような一連の計算の後に置かれると、どちらも優れた効果を発揮します。

層の正規化を簡単に説明すると、行列の値の平均が0になるようにずらし、標準偏差が1になるように調整することです。

長く言うと、transformerのようなシステムでは、多くの動く部品があり、そのうちのいくつかは行列の乗算以外のもの（softmax演算子や整流線形ユニットなど）であり、値がどれだけ大きいか、正と負の間でどうバランスが取れているかが重要である、ということです。すべてが線形であれば、すべての入力を2倍にすれば、出力も2倍になり、すべてがうまく行きます。しかし、ニューラルネットワークはそうではありません。ニューラルネットワークは本質的に非線形であるため、非常に表現力が豊かである一方、信号の大きさや分布に敏感であるという特徴があります。正規化は、何層にもわたるニューラルネットワークにおいて、信号の値の分布をそれぞれのステップで一定に保つために有効な手法です。これにより、パラメータ値の収束が促され、通常、はるかに優れた性能が得られます。

正規化について私が気に入っているのは、先ほどのような高レベルの説明は別として、なぜそれがうまく機能するのか、誰も完全に理解していない点です。このウサギの穴よりもう少し深く入りたい方は、バッチ正規化についてのより詳細な投稿を書いています。これはtransformerで使用される層の正規化の近い親戚にあたります。

複数の層

このように基礎を固めながら、attentionブロックと順伝播ブロックに注意深く選択された重みがあれば、十分な言語モデルを作ることができることを示しました。重みのほとんどは0で1が数個であり、そしてそれらはすべて手作業で選ばれました。生データから学習する場合、このような贅沢は許されません。最初は重みがランダムに選ばれ、そのほとんどがゼロに近く、ゼロでないものはおそらく必要ないものでしょう。モデルがうまく機能するために必要なところから、ずいぶん遠いところにあるのです。

逆伝播法を用いた確率的勾配降下法は非常に素晴らしい結果をもたらしますが、運に左右される部分が多くあります。正しい答えを得るための方法が1つしかない場合、ネットワークがうまく機能するために必要な重みの組み合わせが1つしかない場合、その方法を見つけることはまず不可能です。しかし、良い解に至る経路がたくさんあれば、モデルがそこに到達する可能性はずっと高くなります。

単一のattention層（1つのmulti-head attentionブロックと1つの順伝播ブロック）だけでは、transformerパラメータの良い集合への方法は1つしかありません。すべての行列のすべての要素は、物事がうまく機能するために、正しい値の方法を見つける必要があります。これは壊れやすく脆いもので、パラメータの初期推定値がよほど幸運でない限り、理想からはるかに遠い解に陥ってしまう可能性が高いのです。

transformerがこの問題を回避する方法は、複数のattention層を持ち、それぞれが前の層の出力を入力として使用することです。スキップ接続を使用することで、個々のattentionブロックが破綻したり、奇妙な結果を出力しても、全体的なパイプラインを頑健にすることができます。複数の層があるということは、その分、他の層が待ち構えているということです。もし、あるブロックが軌道から外れたり、その潜在能力を発揮できなかったりしても、下流にある別のブロックがその隙間を埋めるか、誤差を修正する機会を与えてくれます。この論文では、層数が増えるほど性能が向上することが示されていますが、6層目以降ではその向上はわずかなものとなっています。

複数の層を考えるもう一つの方法は、ベルトコンベアー式の組み立てラインと考えることです。それぞれのattentionブロックと順伝播ブロックは、ラインから入力を取り出し、有用なattention行列を計算し、次の単語を予測する機会があります。その結果、有用であろうとなかろうと、コンベアーに戻され、次の層に渡されるのです。

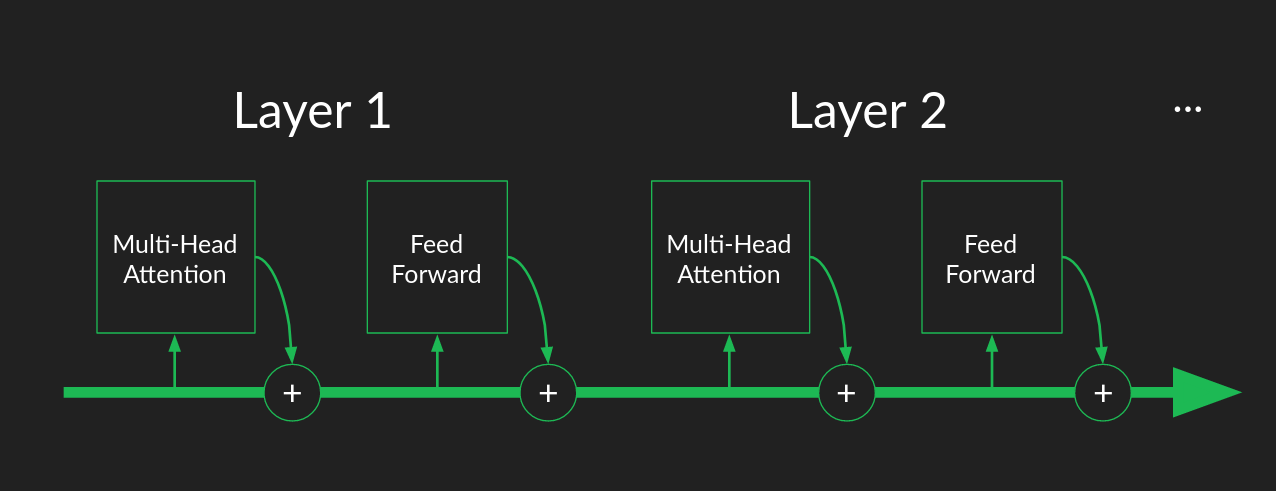
これは、多層ニューラルネットワークを「深い」と表現してきたのとは対照的です。スキップ接続のおかげで、連続する層は冗長性をもたらすのと同じくらい、ますます洗練された抽象化をもたらしません。ある層で見逃された、attentionへの注目や有用な特徴量の生成、正確な予測などの機会は、常に次の層で捕らえることができます。層は組立ラインの労働者のようなものであり、それぞれができることをし、隣の労働者が逃したものを捕まえるため、すべてのピースを捕まえることを気にする必要はありません。

デコーダースタック

これまで私たちは、エンコーダースタック（transformerアーキテクチャの左側）を注意深く無視し、デコーダスタック（右側）を優先してきました。この点については、数段落で修正する予定です。しかし、デコーダーだけでもかなり有用であることに注目する価値があります。

系列補完タスクの説明で敷衍したように、デコーダーは部分的な系列を補完し、好きなだけ拡張することができます。OpenAIは、まさにこれを実現するために、GPT（Generative Pre-Training）モデルファミリーを作りました。彼らがこのレポートで説明しているアーキテクチャは見覚えがあるはずです。これは、エンコーダースタックとその接続をすべて外科的に取り除いたtransformerです。残ったのは12層のデコーダースタックです。

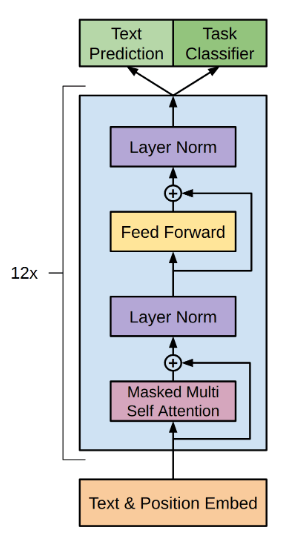
BERT、ELMo、Copilotなどの生成モデルに出会ったとき、あなたはおそらくtransformerの半分のデコーダーが動作しているのを見ていることでしょう。

エンコーダースタック

デコーダーについて学んだことは、ほとんどすべてエンコーダーにも当てはまります。最大の違いは、エンコーダーの性能の善し悪しを判断するのに使えるような、明示的な予測が最後に行われないことです。その代わり、エンコーダースタックの最終的な成果は、埋め込み空間におけるベクトルの系列という、残念なほど抽象的なものです。これは、特定の言語や語彙から切り離された、系列の純粋な意味的表現であると説明されていますが、私にとっては過度にロマンチックに感じられます。私たちが確実に知っているのは、デコーダースタックに意図や意味を伝えるための有用な信号であるということです。

エンコーダースタックがあると、transformerは単に系列を生成するだけでなく、系列をある言語から別の言語に翻訳（または変換）できるようになり、transformerの可能性が広がります。翻訳タスクの学習は、系列補完タスクの学習とは異なります。学習データには、元の言語の系列と、それにマッチするターゲット言語の系列の両方が必要です。原文の言語全体をエンコーダーにかけ、その結果、最後のエンコーダー層の出力が各デコーダー層の入力として提供されます。その後、デコーダーでの系列生成は前と同じように進行しますが、今回はプロンプトを出さずに進めます。

Cross-attention

完全なtransformerを得るための最後のステップは、エンコーダーとデコーダーのスタック間の接続、つまりcross attentionブロックです。このブロックは最後に残しておきましたが、これまで築いてきた基礎のおかげで、あとは説明することはあまりありません。

Cross-attentionは、キー行列Kと値行列Vが前のデコーダー層の出力ではなく、最後のエンコーダー層の出力に基づいていることを除いては、self-attentionと同様に動作します。クエリ行列Qは、やはり前のデコーダー層の結果から計算されます。これは、ソース系列からの情報がターゲット系列に伝わり、その生成を正しい方向に導くためのチャネルです。興味深いのは、デコーダーの各層に同じ埋め込みソース系列が与えられていることであり、連続した層が冗長性をもたらし、同じタスクを実行するために協力し合っているという考え方が裏付けられています。

字句解析

ついにtransformerの全貌が明らかになりました！謎のブラックボックスが残らないよう、十分に詳しく説明しました。私たちが掘り下げなかった実装の詳細がいくつかあります。自分自身で動作するバージョンを構築するためには、それらについて知っておく必要があります。この最後のいくつかの豆知識は、transformerの仕組みというよりも、ニューラルネットワークをうまく動作させるためのものです。The Annotated Transformerはこれらのギャップを埋めるのに役立つでしょう。

しかし、私たちはまだ完全に終わったわけではありません。そもそもデータをどのように表現するかについて、まだ重要なことがあります。これは、自分にとって身近でありながら、おろそかにしがちなテーマです。アルゴリズムの力よりも、データをよく考えて解釈し、その意味を理解することが重要なのです。

語彙は、各単語に1つの要素が関連付けられた高次元のone-hotベクトルで表現できると、ちらっと触れました。これを行うには、表現する単語の数とその内容を正確に把握する必要があります。

素朴な方法としては、Webster's Dictionaryにあるような、すべての可能な単語のリストを作成することです。英語の場合、数万語のリストが作成されますが、正確な数は、何を含めるか、何を除外するかによって異なります。しかし、これは単純化しすぎです。ほとんどの単語には、複数形、所有格、活用形など、いくつかの形があります。単語は別の綴りを持つこともあります。また、データを注意深くクリーニングしない限り、あらゆる種類の誤字脱字が含まれます。さらに、自由形式のテキスト、新語、俗語、専門用語、Unicodeの広大な宇宙によってもたらされる可能性にも触れません。すべての可能な単語を網羅的に列挙すると、途方もなく長くなってしまいます。

合理的な代替案は、単語ではなく、個々の文字が構成要素として機能するようにすることでしょう。文字の網羅的なリストは、私たちが計算できる能力の範囲内です。しかし、これには2つほど問題があります。データを埋め込み空間に変換した後、その空間における距離には意味的な解釈がある、つまり近くにある点は似たような意味を持ち、遠くにある点は全く違う意味を持つと仮定するのです。これにより、ある単語について学んだことを、そのすぐ近くにある単語にも暗黙のうちに拡張することができます。この仮定は、計算効率の点から、またtransformerが一般化する能力の点から頼りにしているものです。

個々の文字レベルでは、意味的な内容はほとんどありません。例えば、英語には1文字の単語がいくつかありますが、それほど多くはありません。絵文字は例外ですが、私たちが見ているほとんどのデータセットでは、絵文字は主要なコンテンツではありません。そのため、埋め込み空間が役に立たないという残念な状態になっています。

理論的には、単語、語幹、単語ペアのような意味的に有用な系列を構築するのに十分な文字の組み合わせを見ることができれば、この問題を回避することは可能かもしれません。残念ながら、transformerが内部的に作成する機能は、順序付けられた入力の集合というよりも、入力ペアの集合のように動作します。つまり、単語の表現は、その順序が強く表現されていない文字ペアの集合になります。transformerは常にアナグラムを扱うことを余儀なくされ、その仕事は非常に困難なものとなります。実際、文字レベルの表現に関する実験では、transformerは文字レベルではあまりうまく動作しないことが分かっています。

バイト対符号化

幸いなことに、これには優れた解決策があります。バイト対符号化と呼ばれるものです。文字レベルの表現から始めて、各文字にコード、それ自身のユニークなバイトが割り当てられます。次に、代表的なデータを走査した後、最も一般的なバイトの対をグループ化し、新しいバイト、新しいコードを割り当てます。この新しいコードをデータに代入し、このプロセスを繰り返します。

文字の対を表すコードは、他の文字や文字の対を表すコードと組み合わせて、より長い文字列を表す新しいコードにすることができます。コードが表現できる文字列の長さに制限はありません。よく繰り返される系列を表現するために必要な分だけ長くすることができます。バイト対符号化の優れた点は、考えられるすべての系列を無造作に表現するのではなく、データからどの長い文字列を学習するかを推論する点にあります。transformerのような長い単語は1バイトのコードで表現できるようになりますが、ksowjmckderのような同じ長さの任意の文字列にはコードを無駄にしないようにします。また、1文字の構成要素に対してすべてのバイトコードを保持するため、奇妙な綴りミスや新語、さらには外国語を表現することも可能です。

バイト対符号化を使用する場合、語彙の大きさを指定すると、その大きさに達するまで新しいコードを構築し続けることができます。語彙のサイズは、文字列がテキストの意味内容を把握するのに十分な長さになるように、十分に大きくする必要があります。文字列は何かを意味するものでなければなりません。そうすれば、transformerを動かすのに十分なほど、語彙が豊富になります。

バイト対符号化器を学習させたり、外部から借用した後は、transformerに送る前にデータの前処理をするために使うことができます。これは、切れ目のないテキストの流れを、一連の異なるチャンク（そのほとんどは、望ましくは認識可能な単語）に分割し、それぞれのチャンクに簡潔なコードを与えるものです。これがトークン化と呼ばれる処理です。

音声入力

さて、この冒険を始めた当初の目的は、音声信号や話し言葉のコマンドをテキスト表現に変換することだったことを思い出してください。ここまでの例では、文字や言葉を扱うことを前提に話を進めてきました。これを音声に拡張することは可能ですが、そのためには信号の前処理をさらに思い切って行う必要があります。

音声信号の情報は、音声を理解するために耳や脳が利用する部分を抽出するために、高度な前処理が必要となります。この方法は、メル周波数ケプストラムフィルタリングと呼ばれ、その名前が示すように、非常にバロック的なものです。このチュートリアルはとても分かりやすく、興味深い内容となっています。

前処理が終わると、生の音声は、それぞれの要素が特定の周波数領域における音声活動の変化を表す、一連のベクトルに変換されます。このベクトルは密度が高く（ゼロの要素はない）、すべての要素が実数値で表されます。

良い面としては、各ベクトルは何かを意味するため、transformerにとって良い「単語」またはトークンになる点です。単語の一部として認識できる音の集合に直接変換することができるのです。

一方、それぞれのベクトルを単語として扱うのは、それぞれが一意であるため、奇妙なことです。音の組み合わせは微妙に違うので、同じベクトル値のセットが2回出てくる可能性は極めて低いのです。これまでのone-hot表現やバイト対符号化の戦略は役に立ちません。

ここで重要なのは、このような実数値の密なベクトルが、単語を埋め込んだ後にできるものであることに着目することです。transformerはこの形式が大好きです。これを利用するには、テキストの例から単語を埋め込むように、ケプストラムの前処理の結果を利用すればよいのです。これにより、トークン化、埋め込みというステップを省くことができます。

このようなことは、他の形式のデータでも可能であることは言うまでもありません。多くの録音データは、密なベクトル列の形で提供されます。これをtransformerのエンコーダーに差し込めば、あたかも単語を埋め込んだかのような状態にすることができます。

まとめ

もし、あなたがまだ私と一緒にいるのなら、ありがとうございます。その価値があったなら幸いです。これで私たちの旅は終わりです。私たちは、想像上の音声制御コンピューター用の音声テキスト変換器を作るという目標でスタートしました。その過程で、私たちは最も基本的な構成要素である数え方と算数から始め、transformerをゼロから再構築しました。自然言語処理の最新技術についての記事を読んだとき、その内部で何が起こっているのかがよく理解でき、満足げに頷けるようになればと願っています。

リソースとクレジット

• 原著論文, Attention is All You Need。
• 非常に便利なtransformerのPython実装。
• Jay Alammar氏による洞察に満ちたtransformerのウォークスルー。
• Lukasz Kaiser氏（著者の一人）によるtransformerの仕組みを説明した講義。
• Googleスライドの図解。

Brandon
2021年10月29日

脚注

1. （訳注: ヨハネによる福音書 1章1:1、「初めに言があった。」のオマージュ。）

2. （訳注: convertもtransduceも「変換」だし、どうしようもない😥）

3. （訳注: 厳密にはdot productは「ドット積」ですが、この記事では「内積」と訳すことにします。）