勾配ブースティングを自分で実装してみる
概要
勾配ブースティングは、2023年現在最も広く使われている機械学習アルゴリズムの一つです。[1]
勾配ブースティングを実装したライブラリとしてはXGBoostやLightGBMなどが有名で、これらを使うことで高速かつ高精度な機械学習モデルを簡単に構築することが出来ます。
実際に自分でもこれらのライブラリを日常的に使っているのですが、よく使うものなので自分でも実装してみることで良い学びが得られるような気がしています。
そこで、本記事では勾配ブースティングのアルゴリズムを自分で実装してみようと思います。
実装の方針は以下の通りです。
- 最もよく使われる弱学習器として決定木を使う手法[2]を実装します。
- 参考資料としては、XGBoostの公式チュートリアル内のIntroduction to Boosted Treesという記事を用います。
- あくまでも勉強目的なので、簡潔で分かりやすい実装を目指します。
参考資料として用いるIntroduction to Boosted Treesはかなり短い記事ですが、勾配ブースティングのアルゴリズムをミニマルに実装するのには十分な情報が含まれていると思うので、ひとまずこの記事だけを参考にして実装します。
その後、以下の各問題に対し自分で実装した勾配ブースティングとXGBoostをそれぞれ適用し比較することで、本当にちゃんと実装できているかどうかを確認します。
- 2クラス分類
- 回帰
- 多クラス分類
想定読者
本記事では勾配ブースティングとは何かなどの解説は基本的に行わず実装にフォーカスします。
したがって、以下の少なくとも一方の条件を満たす方が想定読者となります。
- 勾配ブースティングについて既に知っている
- Introduction to Boosted Treesを読んで理解できる
Introduction to Boosted Trees のまとめ
実装に入る前に、参考資料から実装に関係する部分を抜粋して簡単にまとめます。
目的関数の定義
まず、目的関数を以下のように定義します。
ここで、
損失関数は問題設定により適切なものを選びます。正則化項には色々なものが考えられますが、経験的には以下のような正則化項が上手く機能するらしいので、以下ではこの正則化項を前提に説明します。
Additive Training
上で定義した目的関数を最小化するようなモデルを一気に学習できると良いのですが、実際には全ての木を同時に学習するのは難しいです。
そこで勾配ブースティングでは、1つ1つの木を順番に学習し既に出来ているモデルに足していくという方策をとっており、これをAdditive Trainingと呼びます。
1本ずつ木を学習することになるので、上で示した大局的な目的関数ではなく、1本の木に対する目的関数を用意する必要があります。
とはいえこれは単純な話で、例えば
目的関数の近似
これで無事モデルの学習が出来るかというとそうでもなく。損失関数によっては最適化がややこしくなるという問題が残されています。
例えば損失関数が2乗誤差の場合、下で示すように最適なスコアや目的関数の値などを解析的に求めることが出来ますが、一般の損失関数について考えるとそうはいかないことが多いです。
なので、実際には目的関数を
ただし
2次近似したことにより、最適なスコアと最適なスコアを選んだ場合の目的関数の値を解析的に求めることができます。
木の構造の学習
決定木
しかし、あらゆる木の構造を全て列挙するということは現実的にはほぼ不可能なので、ここでまた1つヒューリスティクスを導入することになります。
ここで導入するヒューリスティクスは、木のノードを分割するかどうかを1つ1つ判断していく、というものです。
アルゴリズム的には、データを実際に決定木に入力してみて各ノードでそこから更に分割を行うべきかを判断しながら木を伸ばしていくという手順になります。
木を分割するかどうかの判断には以下の式で定義されるゲインを用います。
これは「分割しなかった場合の目的関数の値」から「分割した場合の目的関数の値」を引いた式で、これにより目的関数の値がどれくらい減るかを評価します。
ゲインが0より大きいならば目的関数の値を小さくすることが出来るということなのでノードを分割します。逆に、そうでなければノードを分割しません。
実装
以下の3ステップに分けて実装していきます。
- 目的関数を実装する
- 単一の決定木の学習を実装する (弱学習器)
- 弱学習器の学習を繰り返して強学習器を構築する
目的関数の実装
目的関数としては色々なものを考えることが出来ますが、本文中でも登場したsquared errorとlogistic lossを実装することにします。
参考資料でも述べられていた通り、目的関数の1次微分(grad)と2次微分(hess)を実装する必要があります。
ちなみに、今回の用途では目的関数そのもの(loss)は実装する必要がありませんが、何となく気持ちが悪いので一応実装しています。
import numpy as np
class SqueredError:
def loss(self, y, y_pred):
return (y - y_pred) ** 2
def grad(self, y, y_pred):
return -2 * (y - y_pred)
def hess(self, y, y_pred):
return np.ones_like(y_pred) * 2
class LogisticLoss:
def loss(self, y, y_pred):
return y * np.log(1 + np.exp(-y_pred)) + (1 - y) * np.log(1 + np.exp(y_pred))
def grad(self, y, y_pred):
return - y * np.exp(-y_pred) / (1 + np.exp(-y_pred)) + (1 - y) * np.exp(y_pred) / (1 + np.exp(y_pred))
def hess(self, y, y_pred):
return (
y * np.exp(-y_pred) / (1 + np.exp(-y_pred))
- y * np.exp(-2*y_pred) / (1 + np.exp(-y_pred)) ** 2
+ (1 - y) * np.exp(y_pred) / (1 + np.exp(y_pred))
- (1 - y) * np.exp(2*y_pred) / (1 + np.exp(y_pred)) ** 2
)
単一の決定木 (弱学習器) の学習
続いて、Additive Training における、単一の決定木の学習を実装します。
実装上一番面倒なのがこの部分なので、このセクションが本記事のハイライトと言っても良いでしょう。
出来る限り参考資料に忠実に実装したつもりなので、参考資料と比較しながら読んでいただければと思います。
class DecisionTree:
def __init__(self, reg_lambda, gamma):
"""
reg_lambda: L2正則化項の係数
gamma: 葉の数を制限するための係数
"""
self.reg_lambda = reg_lambda
self.gamma = gamma
def fit(self, X, y, grad, hess):
"""
X: 訓練データの特徴量 shape=(N, D)
y: 訓練データの目的変数 shape=(N,)
grad: 訓練データの1次微分 shape=(N,)
hess: 訓練データの2次微分 shape=(N,)
"""
# 最適な分割を探索する
n_cols = X.shape[1]
best_gain = 0
for i in range(n_cols):
threshold, gain = self.find_best_split(X[:, i], y, grad, hess)
if best_gain < gain:
best_gain = gain
best_threshold = threshold
best_col = i
# 0 < Gain となる分割が見つからなかった場合は葉ノードとする
if best_gain == 0:
self.is_leaf = True
self.score = self.calc_best_score(grad, hess)
return self
# 0 < Gain となる分割が見つかった場合は更に分割する
self.is_leaf = False
self.column_idx = best_col
self.threshold = best_threshold
x_best = X[:, best_col]
is_left = x_best < best_threshold
is_right = best_threshold <= x_best
self.left = DecisionTree(self.reg_lambda, self.gamma).fit(X[is_left], y[is_left], grad[is_left], hess[is_left])
self.right = DecisionTree(self.reg_lambda, self.gamma).fit(X[is_right], y[is_right], grad[is_right], hess[is_right])
return self
def find_best_split(self, x, y, grad, hess):
"""
[引数]
x: 1つの特徴量 shape=(N,)
y: 目的変数 shape=(N,)
grad: 1次微分 shape=(N,)
hess: 2次微分 shape=(N,)
[返り値]
best_threshold: 最適な分割の閾値 (見つからなかった場合はNone)
best_gain: 最適な分割のGain (見つからなかった場合は0)
"""
# 各データをxの値でソートする
sort_idx = x.argsort()
x = x[sort_idx]
y = y[sort_idx]
grad = grad[sort_idx]
hess = hess[sort_idx]
# 計算量を削減するために累積和を使う
cgrad = np.cumsum(grad)
chess = np.cumsum(hess)
# 閾値の探索
best_threshold = None
best_gain = 0
for i in range(1, len(x)):
# x[i] == x[i-1] ならここで分割する意味がないのでスキップする
if x[i] == x[i-1]:
continue
# Gainを計算・更新する
gl, hl = cgrad[i-1], chess[i-1]
gr, hr = cgrad[-1] - cgrad[i-1], chess[-1] - chess[i-1]
gain = self.calc_gain(gl, hl, gr, hr)
if best_gain < gain:
best_gain = gain
best_threshold = (x[i] + x[i-1]) / 2
return best_threshold, best_gain
def predict(self, X):
"""
X: 特徴量 shape=(N, D)
"""
# 葉ノードなら単純にスコアを返す
if self.is_leaf:
return np.zeros(len(X)) + self.score
# 葉ノードでないなら再帰的にスコアを求めて返す
x = X[:, self.column_idx]
is_left = x < self.threshold
is_right = self.threshold <= x
y_pred = np.empty_like(x)
y_pred[is_left] = self.left.predict(X[is_left])
y_pred[is_right] = self.right.predict(X[is_right])
return y_pred
def calc_best_score(self, gj, hj):
"""
葉jのスコアを計算する
gj: 葉jに属するサンプルの1次微分
hj: 葉jに属するサンプルの2次微分
"""
return - np.sum(gj) / (np.sum(hj) + self.reg_lambda)
def calc_gain(self, gl, hl, gr, hr):
"""
分割により得られるゲインを計算する
gl: 左の子ノードに属するサンプルの1次微分
hl: 左の子ノードに属するサンプルの2次微分
gr: 右の子ノードに属するサンプルの1次微分
hr: 右の子ノードに属するサンプルの2次微分
"""
Gl, Hl, Gr, Hr = gl.sum(), hl.sum(), gr.sum(), hr.sum()
return (
Gl**2 / (Hl + self.reg_lambda)
+ Gr**2 / (Hr + self.reg_lambda)
- (Gl + Gr)**2 / (Hl + Hr + self.reg_lambda)
) / 2 - self.gamma
強学習器の構築
目的関数(objective)と弱学習器(DecisionTree)の実装が出来ていれば、強学習器(GBDT)の実装は簡単です。
特に解説すべき点もありませんが、ハイパーパラメータとしてlearinng_rateを取れるようにしたのは目新しい点と言えるかもしれません。
class GBDT:
def __init__(self, objective, n_estimators=100, reg_lambda=0, gamma=0, learning_rate=1):
"""
objective: 目的関数
n_estimators: 決定木の数
reg_lambda: L2正則化項の係数
gamma: 葉の数を制限するための係数
learning_rate: 学習率
"""
self.objective = objective
self.n_estimators = n_estimators
self.reg_lambda = reg_lambda
self.gamma = gamma
self.learning_rate = learning_rate
def fit(self, X, y):
self.trees = []
y_pred = np.zeros(len(X))
for _ in range(self.n_estimators):
grad = self.objective.grad(y, y_pred)
hess = self.objective.hess(y, y_pred)
tree = DecisionTree(self.reg_lambda, self.gamma)
tree.fit(X, y, grad, hess)
y_pred += self.learning_rate * tree.predict(X)
self.trees.append(tree)
def predict(self, X):
y_pred = np.zeros(len(X))
for tree in self.trees:
y_pred += self.learning_rate * tree.predict(X)
return y_pred
実験
上で説明した勾配ブースティングの実装を実際に簡単なデータに適用し、それらしいモデルが学習できるかを試してみます。
具体的には、以下の3種類の問題に対して上の実装とXGBoostでそれぞれモデルを学習して、学習されたモデルの内容を比較します。
- 2クラス分類
- 回帰
- 多クラス分類
なお、上で説明したコードはmy_gbdt.pyというファイルにまとめてあり、実験の際にはfrom my_gbdt import LogisticLoss, GBDTのようにインポートして使うこととします。
実験条件
以下の実験は全て Windows 11 上で行いました。
Pythonおよび、主要なパッケージのバージョンは以下の通りです。
- Python 3.10.9
- XGBoost 1.7.3
- NumPy 1.24.2
実験1: 2クラス分類
まずは、簡単な例として2クラス分類問題に対して適用してみます。
作成したデータはscikit-learnのmake_circlesという関数を使って作ったもので、2次元の円状のデータとそれを取り囲む輪のようなデータの2つのクラスから成ります。
これに対して、上で実装したGBDTクラスと、XGBoostのXGBClassifierを使ってそれぞれモデルを学習し、学習されたモデルの内容を可視化して比較します。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
import xgboost
from xgboost import XGBClassifier
from my_gbdt import LogisticLoss, GBDT
def train_my_model(X, y):
my_model = GBDT(LogisticLoss(), n_estimators=5, reg_lambda=1, gamma=1, learning_rate=1)
my_model.fit(X, y)
return my_model
def train_xgb_model(X, y):
xgb_model = XGBClassifier(
objective='binary:logistic', n_estimators=5, reg_lambda=1, gamma=1, learning_rate=1,
max_depth=None, tree_method='exact', min_child_weight=0,
)
xgb_model.fit(X, y)
return xgb_model
def visualize_result(X, y, my_model, xgb_model):
plt.style.use('ggplot')
fig, axes = plt.subplots(nrows=1, ncols=2, sharex=True, sharey=True, figsize=(10, 5))
# 各モデルの予測結果を可視化
x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
## my_model の予測結果
axes[0].contourf(xx, yy, (0 < my_model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)).astype(int), alpha=0.4, cmap='bwr')
axes[0].scatter(X[:, 0], X[:, 1], c=y, cmap='bwr')
axes[0].set_title(f'My model on train data')
## xgb_model の予測結果
axes[1].contourf(xx, yy, (xgb_model.predict(np.c_[xx.ravel(), yy.ravel()])).reshape(xx.shape), alpha=0.4, cmap='bwr')
axes[1].scatter(X[:, 0], X[:, 1], c=y, cmap='bwr')
axes[1].set_title(f'XGBoost on train data')
# グラフを保存
fig.savefig('figures/binary_experiment.png', bbox_inches='tight')
if __name__ == '__main__':
X, y = make_circles(n_samples=1000, noise=0.1, factor=0.2, random_state=0)
my_model = train_my_model(X, y)
xgb_model = train_xgb_model(X, y)
visualize_result(X, y, my_model, xgb_model)
以下の図が出来上がったグラフです。
赤い点と青い点がそれぞれのクラスに相当する学習データになっていて、背景が赤くなっている領域と青くなっている領域がそれぞれモデルによって赤クラスと判定された領域と青クラスと判定された領域になっています。
この図より、自作モデルとXGBoostのモデルの予測結果は若干は違うものの、どちらも学習自体は上手く出来ているということが分かります。[3]

予測結果だけでなく、学習された木の構造も可視化して確認してみましょう。
以下のような関数を用意して、学習された木を引数に渡すことで学習された木の構造を可視化することが出来ます。
(なお、XGBoostについてはxgboost.to_graphvizという関数を用いることで同様の可視化を行うことが出来るのでそちらを使っています。)
import graphviz
def show_tree(tree):
def traverse(tree, digraph, node_idx):
if tree.is_leaf:
digraph.node(str(node_idx), f'leaf={tree.score:.9g}')
return node_idx
# left
digraph.node(str(node_idx), f'f{tree.column_idx}<{tree.threshold:.9g}')
digraph.edge(str(node_idx), str(node_idx + 1), label='Yes', color='blue')
left_idx = traverse(tree.left, digraph, node_idx + 1)
# right
digraph.edge(str(node_idx), str(left_idx + 1), label='No', color='red')
right_idx = traverse(tree.right, digraph, left_idx + 1)
return right_idx
digraph = graphviz.Digraph()
traverse(tree, digraph, 0)
return digraph
自作モデルとXGBoostの0番目の木を可視化してみた結果は以下の通りです。
一見すると結構違うように思えますが、よく見ると部分的にはほぼ同じ木になっていてXGBoostの方が若干多く分岐しているのが違いだということが分かります。

自作モデルの0番目の木

XGBoostの0番目の木
両者の違いがどのような原因で生じるのかまだ完全には理解できていませんが、本記事の趣旨はXGBoostを完全再現することではないのでひとまず深入りはしないでおきます。[4]
実験2: 回帰
次に、損失関数を別のものに変えても動くのかということを確認するために簡単な回帰問題に適用してみます。
以下では、正弦波の値にノイズを加えたデータを用意して、単純な1次元の回帰モデルを学習しています。
import matplotlib.pyplot as plt
import numpy as np
from xgboost import XGBRegressor
from my_gbdt import SqueredError, GBDT
def make_data():
np.random.seed(0)
X = np.linspace(0, 2*np.pi, 1000).reshape(-1, 1)
y = np.sin(X.ravel()) + np.random.randn(len(X)) * 0.1
return X, y
def train_my_model(X, y):
my_model = GBDT(SqueredError(), n_estimators=10, reg_lambda=1, gamma=1, learning_rate=1)
my_model.fit(X, y)
return my_model
def train_xgb_model(X, y):
xgb_model = XGBRegressor(
objective='reg:squarederror', n_estimators=10, reg_lambda=1, gamma=1, learning_rate=1,
max_depth=None, tree_method='exact', min_child_weight=0,
)
xgb_model.fit(X, y)
return xgb_model
def visualize_result(X, y, my_model, xgb_model):
plt.style.use('ggplot')
fig, axes = plt.subplots(nrows=1, ncols=3, sharex=True, sharey=True, figsize=(15, 5))
# 学習データを可視化
axes[0].plot(X, y, 'o', markersize=2, label='Train data')
axes[0].plot(X.ravel(), np.sin(X.ravel()), label='Best model')
axes[0].set_title('Train data')
axes[0].legend()
# my_model の予測結果
x = X.ravel()
axes[1].plot(x, my_model.predict(X), label='Trained model')
axes[1].plot(x, np.sin(x), label='Best model')
axes[1].set_title('My model')
axes[1].legend()
# xgb_model の予測結果
axes[2].plot(x, xgb_model.predict(X), label='Trained model')
axes[2].plot(x, np.sin(x), label='Best model')
axes[2].set_title('XGBoost model')
axes[2].legend()
# グラフを保存
fig.savefig('figures/regression_experiment.png', bbox_inches='tight')
if __name__ == '__main__':
X, y = make_data()
my_model = train_my_model(X, y)
xgb_model = train_xgb_model(X, y)
visualize_result(X, y, my_model, xgb_model)
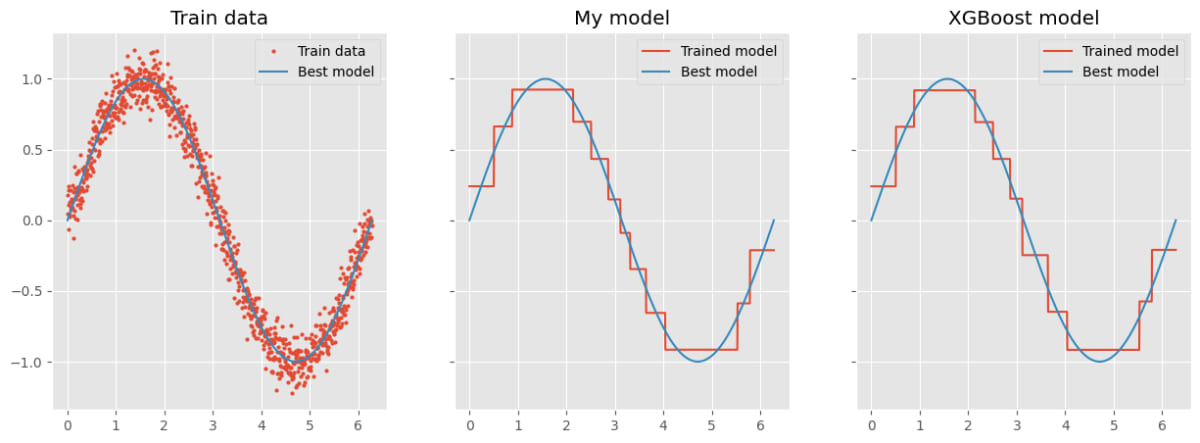
実験の結果は以下の通りです。左側のグラフは学習データをプロットしたものです。
赤色の点が実際に学習に使われたデータで、青色の線は学習データの生成元になった正弦波です。[5]
真ん中のグラフと右側のグラフがそれぞれ自前の実装とXGBoostの結果です。
粗めのパラメータにしたのでかなりカクカクしていますが、どちらも似たような感じになっています。
実験3: 多クラス分類
実験に入る前にまず、1次元のデータしか出力できないこれまでのモデルで、多クラス分類問題を実装する方法について考える必要があります。
参考までにXGBoostではどうしているのか調べてみたところ、XGBClassifierで目的変数のクラスが3つ以上ある場合は各クラスに対してモデルを学習して、それぞれのモデルを組み合わせることで多クラス分類を実現しているようだと分かりました(One-vs-Rest)。[6]
ということで、こちらの実装でも同様に、各クラスに対してそれに属するかを判定するモデルを学習し、予測の時はそれぞれのモデルのスコアを比較して最もスコアが高いクラスを予測結果とするようにしてみます。
具体的な実装は以下の通りです。上で実装したGBDTクラスを使いまわすことで簡単に実装することができました。
class GBDTMulticlass:
def __init__(self, objective, n_estimators=100, reg_lambda=0, gamma=0, learning_rate=1):
"""
objective: 目的関数
n_estimators: 決定木の数
reg_lambda: L2正則化項の係数
gamma: 葉の数を制限するための係数
learning_rate: 学習率
"""
self.objective = objective
self.n_estimators = n_estimators
self.reg_lambda = reg_lambda
self.gamma = gamma
self.learning_rate = learning_rate
def fit(self, X, y):
n_classes = len(np.unique(y))
self.models = []
for k in range(n_classes):
y_k = (y == k).astype(int)
model = GBDT(self.objective, self.n_estimators, self.reg_lambda, self.gamma, self.learning_rate)
model.fit(X, y_k)
self.models.append(model)
def predict(self, X):
n_classes = len(self.models)
y_pred = np.empty((len(X), n_classes))
for k in range(n_classes):
y_pred[:, k] = self.models[k].predict(X)
return np.argmax(y_pred, axis=1)
では、多クラスに対応したGBDTMulticlassを使って、多クラス分類のモデルを学習してみましょう。
ここでは、マス目上に二次元正規分布が並んでいて、それぞれの正規分布がどれかのクラスに対応しているというデータを作成して実験を行っています。
import matplotlib.pyplot as plt
import numpy as np
from xgboost import XGBClassifier
from my_gbdt import LogisticLoss, GBDTMulticlass
def make_data():
"""
[ 作成するデータ ]
* 3 x 3 のマス目上に二次元正規分布を並べたもの。
* 3クラス分類問題のためのデータで、それぞれの正規分布がどれかのクラスに対応している。
"""
np.random.seed(seed=9)
X = np.empty((900, 2))
y = np.empty(900)
for i in range(9):
cx, cy = i // 3, i % 3
X[100*i:100*(i+1), :] = 0.15 * np.random.randn(100, 2) + (cx, cy)
y[100*i:100*(i+1)] = np.random.randint(3)
return X, y
def train_my_model(X, y):
my_model = GBDTMulticlass(LogisticLoss(), n_estimators=10, reg_lambda=1, gamma=1, learning_rate=1)
my_model.fit(X, y)
return my_model
def train_xgb_model(X, y):
xgb_model = XGBClassifier(
objective='multi:softmax', n_estimators=10, reg_lambda=1, gamma=1, learning_rate=1,
max_depth=None, tree_method='exact', min_child_weight=0,
)
xgb_model.fit(X, y)
return xgb_model
def visualize_result(X, y, my_model, xgb_model):
plt.style.use('ggplot')
fig, axes = plt.subplots(nrows=1, ncols=2, sharex=True, sharey=True, figsize=(10, 5))
# 各モデルの予測結果を可視化
x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
## my_model の予測結果
axes[0].contourf(xx, yy, my_model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape), alpha=0.4)
axes[0].scatter(X[:, 0], X[:, 1], c=y, marker='o', edgecolors='k')
axes[0].set_title(f'My model on train data')
## xgb_model の予測結果
axes[1].contourf(xx, yy, xgb_model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape), alpha=0.4)
axes[1].scatter(X[:, 0], X[:, 1], c=y, marker='o', edgecolors='k')
axes[1].set_title(f'XGBoost on train data')
# グラフを保存
fig.savefig('figures/multiclass_experiment.png', bbox_inches='tight')
if __name__ == '__main__':
X, y = make_data()
my_model = train_my_model(X, y)
xgb_model = train_xgb_model(X, y)
visualize_result(X, y, my_model, xgb_model)
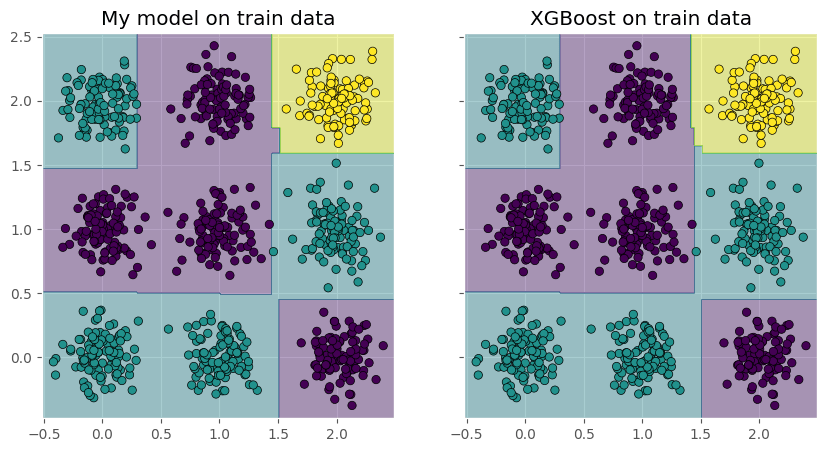
実験の結果は以下の図の通りです。
図の見方は2クラス分類の時と同じで、各点の色が学習データが属するクラスを表していて、背景の色がモデルによって予測されたクラスを表しています。
図から、やはり若干異なる部分はあるものの、どちらも学習は上手くできているということが分かります。
おわりに
個人的には結構分かりやすく実装できたと満足しているのですが、XGBoostの結果とちょっと異なる感じになるのは少し気になる点です。
モデル自体は上手く学習出来ているようなので、あまり重大ではない違いが幾つかあるんだろうと思っていますが実際どうなんでしょうね。
-
個人の感想です。 ↩︎
-
Gradient Boosted Trees とか、Gradient Boosted Decision Trees (GBDT) などと呼ばれるようです。 ↩︎
-
Trainデータに対するAccuracyはどちらも100%です。 ↩︎
-
分かっている範囲で言うと、まずXGBoostは内部的には32bitの数値を使っているらしいのに対し、自分の実装では64bitの数値を使っているということがあります。こちらの方でも32bitの数値を使うようにするというのは試しましたが、そうすると図中の閾値や葉のスコアの値が完全に一致するようだということは確認出来ています。
他にも、もしかすると把握できていない範囲で何らかの条件が異なっているとか、そういうことはあるかもしれませんが確認しきれていません。 ↩︎ -
「究極に上手く学習出来た場合はこの曲線になる」という理由でBest modelというラベルが付いています。 ↩︎
-
例えば、n_estimators=1で3クラス分類問題のモデルを作ると木が3つ出来る。 ↩︎
Discussion