🎉
論文まとめ: AWQ

2025/05/20に公開
 はじめにAWQ により量子化されているモデルをよく見かける。例えば、Qwen/Qwen3-8B-AWQなどである。この手法が具体的にどのような方法なのか気になったので調べた。自身の理解度を高めるために、まとめて公開する。

 注意論文中では、量子化アルゴリズム AWQ についてと、推論フレームワークの TinyChat について紹介されているが、自分の興味は AWQ のみのため、TinyChat については割愛する。

 論文メタ情報
 タイトルAWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration

 URLhttps://arxiv.org/abs/2306.00978

 著者Ji Lin * 1

Jiaming Tang * 1 2

Haotian Tang † 1

Shang Yang † 1

Wei-Ming Chen 3

Wei-Chen Wang 1

Guangxuan Xiao 1

Xingyu Dang 1 4

Chuang Gan 5 6

Song Han 1 3
*: Algorithm co-lead,

†: system co-lead.
1: MIT

2: Shanghai Jiao Tong University

3: NVIDIA

4: Tsinghua University

5: MIT-IBM Watson AI Lab

6: UMass Amherst.

Correspondence to: Song Hansonghan@mit.edu.

 学会Proceedings of the 7th MLSys Conference, Santa Clara, CA, USA, 2024.

 概要LLM はすごいけれど、重いのは問題である。
Activation-aware Weight Quantization (AWQ) を提案する。
AWQ は 1% の重要な重みを保護するだけで、量子化誤差を大幅に削減できる。
重要な重みチャネルの識別には、重みではなく、活性化分布を参照する必要がある。
AWQ は、重要な重みチャネルを保護するために、活性の値を用いてスケーリングを行う。
AWQ はバックプロパゲーションや再構成に依存しないため、モデルがキャリブレーションデータに過剰適合しない。
Instruction Tuning された LM において優れた量子化性能を実現し、初めてマルチモーダルモデルにも対応した。

 背景量子化を考慮したトレーニング (Quantization-aware training, QAT) はトレーニングコストが高いため効率的ではなく、トレーニング後の量子化 (post-training quantization, PTQ) は低ビット設定で精度が大きく低下する。
PTQ における LLM の量子化には、大きく２つの手法がある。
(1) W8A8 量子化

活性化と重みの両方を INT8 に量子化する
(2) W4A16 量子化

重みのみを低ビット整数に量子化する
AWQ では、必要なメモリを少なくし、トークン生成を高速にするために、W4A16 量子化に焦点を当てる。
AWQ に最も近い手法は、GPTQ (Frantar+ 2022)である。これは、再学習なしに量子化後の誤差を最小化する手法である。しかし GPTQ は、キャリブレーションデータに過剰適合しやすく、別のタスクでは性能低下するという課題が存在する。

 提案手法提案手法を以下の図にまとめる。

図の左(a)は、Round-To-Nearest (RTN) による方法を説明している。RTN は、元の重み行列 W（FP16）を、そのまま 3 bit 整数に丸める方法である。量子化誤差が大きくなり、OPT-6.7B の例では Perplexity が 43.2 であった。
図の中央(b)は、重要ではない重みを INT3 に変換し、重要な重みを FP16 で残す方法を説明している。

入力活性 X の分布を調べると、計算結果に強く寄与する列が 1 % 程度しかないことが分かった。そこだけ FP16 のまま保持し、残り 99 % を 3 bit に量子化する方法を行うと、Perplexityは、OPT-6.7Bの例で 13.0 まで改善した。しかし、行列内に FP16 と INT3 が混在する mixed-precision になるため、メモリアクセスや計算カーネルが複雑になり、ハードウェア効率が落ちる。
図の右(c)は、AWQ による量子化を示している。重要な列を量子化前にスケール係数 α で持ち上げ、全列を一律に 3 bit 量子化する手法である。スケールによって重要列の情報を保護できるため、すべてを INT3 に量子化しても Perplexity 13.0 を維持できる。よって、精度は(b)と同等であり、すべて低ビット整数なのでメモリも計算も軽い。
以下から、より具体的な手法の説明を行う。

 前提量子化済み線形層は以下のように表現される。

\mathbf{y}\;\approx\;Q(\mathbf{w})\,\mathbf{x} \tag{1}
ここで、

Q(\mathbf{w}) \;=\; \Delta \,\cdot\, \operatorname{Round}\!\left(\frac{\mathbf{w}}{\Delta}\right),
\qquad 
\Delta \;=\; \frac{\max\!\left(|\mathbf{w}|\right)}{2^{N-1}} \tag{2}
である。
\Delta は量子化スケーラーである。

 重みを拡大し、活性を縮小する活性が大きい、つまり重要なチャネル(列)は全体の 1% だった。そこで、活性が大きいチャネルの重みのみを保護し、それ以外は量子化することで、高い精度と省メモリの両方を実現する。

具体的には、チャネルごとの係数 s を導入する。式(1)に対し、 s を重みにかけて、活性は s で割る。具体的には以下の式のようにする。

Q(w \cdot s)\cdot\frac{x}{s}
\;=\;
\Delta'\,\cdot\,\operatorname{Round}\!\left(\frac{ws}{\Delta'}\right)\,x\cdot\frac{1}{s}
\tag{3}
また、\Delta' は新しい量子化スケーラーである。

 量子化誤差がどれだけ減るか結論から先に説明すると、量子化誤差は 1/s となる。
そのことを数式的に説明するために、以下３つの前提を説明する。
(1) Round の期待誤差 RoundErr は AWQ の適用前後で変化せず、0.25である。このことを直感的に理解するために、float -> int への量子化の例をいくつか考える。最も誤差が少ない例では0.0 -> 0となり、その差は0であり、最も誤差が大きい例では0.5 -> 0となる。平均的な誤差、つまり期待誤差は 0.0 ~ 0.5 の平均、つまり 0.25 程度となりそうだと分かる。
(2) w をスケーリングしても、スケーリングされる重要な重みはごく一部のため、グループ \mathbf{w} の最大値は変化しないことが多い。したがって、\Delta' \approx \Delta となる。
(3) \Delta と x は FP16 で表されるため、量子化誤差は存在しない。
よって、以下の式が成立する。

\begin{align*}
&\frac{\text{AWQ適用後の量子化誤差}}{\text{AWQ適用前の量子化誤差}} \\[1.5ex]
&= \frac{\mathrm{Err}\left(Q(w \cdot s)\left( \frac{x}{s} \right)\right)}{\mathrm{Err}(Q(w)x)} \\[1.5ex]
&= \frac{\Delta' \cdot \mathrm{RoundErr}\left( \frac{ws}{\Delta'} \right) \cdot x \cdot \frac{1}{s}}{\Delta \cdot \mathrm{RoundErr}\left( \frac{w}{\Delta} \right) \cdot x} \\[1.5ex]
&= \frac{\Delta'}{\Delta}
\cdot
\frac{\mathrm{RoundErr}\left( \frac{ws}{\Delta'} \right)}{\mathrm{RoundErr}\left( \frac{w}{\Delta} \right)}
\cdot \frac{1}{s} \\[1.5ex]
&\approx \frac{1}{s}
\end{align*}
利用している前提も追加すると以下のようになる。

上記式より、誤差は 1/s となることが分かる。

 スケール係数 \mathbf{s} の求め方スケール係数 \mathbf{s} は、以下の損失関数 \mathcal{L(s)} を最小にするように選ばれる。式にすると、以下のようになる。

\mathbf{s}^* = \arg\min_{\mathbf{s}} \mathcal{L}(\mathbf{s})
損失関数は以下のように定義される。

\mathcal{L}(\mathbf{s}) = \left\| Q(\mathbf{W} \cdot \mathrm{diag}(\mathbf{s}))(\mathrm{diag}(\mathbf{s})^{-1} \cdot \mathbf{X}) - \mathbf{W}\mathbf{X} \right\|
\mathbf{W}：FP16 の重み行列（量子化対象）

\mathbf{X}：キャリブレーション用の入力データ

Q(⋅)：低ビット整数への量子化操作

\mathrm{diag(s)}：スケーリング係数 \mathbf{s} の対角行列

\mathrm{diag}(s)^{-1}：スケーリング係数 \mathbf{s} の逆数の対角行列

\mathcal{L}(\mathbf{s})：スケーリング後の量子化出力と元の出力 WX との量子化誤差
最後に、s_iは以下のように与えられる。

s_i = \bar{x}_i^{\alpha}
\alpha は 0〜1 のパラメータであり、\alpha をグリッドサーチして、\mathcal{L(s)} を最小化する \alpha を選択する。
この手法は、勾配や再学習が不要であり、非常に高速である。

 実験
Table 4より、AWQ は、RTN や GPTQ などの手法よりも PPL が低いことが分かる。
Table 5より、AWQ は、GQA(Grouped Query Attention)やMixture-of-Experts(MoE)モデルに対しても、PPL を維持しつつ、量子化をすることが可能であることが分かる。
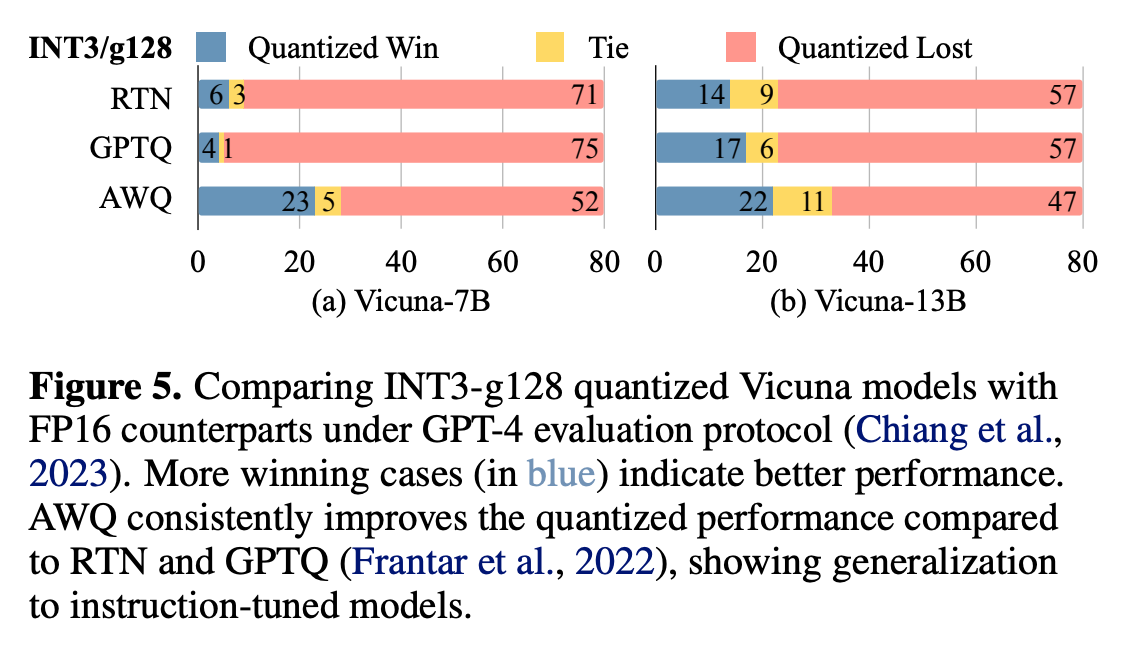
Figure 5にて、GPT-4 evaluation protocol (Chiang et al., 2023) に従って、量子化モデルと FP16 モデルのどちらが優れているかの評価を行った結果を示す。結果は Win, Tie, lost の３つのどれかである。Win とは、量子化モデルの方が、FP16 モデルよりも性能が良いと判断されたことを示す。
RTN や GPTQ に比べ、AWQ では Win や Tie の割合が増えており、量子化後の精度を改善できていることが分かる。


Table 6にVision Language Model(VLM)に対するAWQを適用した実験の結果を載せた。AWQはキャリブレーションセットへの過剰適合の問題がないため、VLMに直接適用できる。VLMにおいても、AWQはRTNやGPTQよりも高い性能を維持することができる。なお、Language Modelがモデルの大部分を占めるため、Language Model部分のみを量子化した。これは、我々の知る限り、VLM低ビット量子化に関する初の研究である。
Table 7より、様々な visual-language benchmarksにおいて、性能を維持できることが分かる。
Table 8は、Python programming の問題である MBPP dataset に対する CodeLlama-7bInstruct-hf の性能と、数学の問題である GSM8K dataset に対する Llama-2 (7B/13B/70B) に対して AWQ を適用した際の性能である。
Programming の問題、数学の問題の両方について、RTN や GPTQ よりも性能が高い。
Figure 8 について、左の図より、キャリブレーションデータのシーケンス数(図中では、calibration sequences)が少なくても、GPTQ に対して AWQ の方が Perplexitiy が良いことが分かる。
右の表より、GPTQ は較正データと評価データを別データで行った場合に Perplexitiy が悪化していることが分かる。例えば、Calib と Eval のデータセットの組み合わせを(Calib, Eval)のように表記した場合に、GPTQ は(PubMed, PubMed)の性能と(PubMed, Enron)に性能を比較すると、Perplexitiy が 2.33 悪化する。一方、AWQ は同様の条件でも Perplexitiy が 0.60 しか悪化しないことが実験的に示されている。よって、AWQ はモデルがキャリブレーションデータに過剰適合しないことが分かる。

 まとめ低ビット重みのみの LLM 圧縮のためのシンプルかつ効果的な手法である Activation-aware Weight Quantization (AWQ) を提案した。
LLM における重みの重要性は必ずしも等しくないという観察に基づき、AWQ はチャネルごとにスケーリングを行うことで、顕著な重みの量子化損失を低減する。
AWQ はキャリブレーションセットを過剰適合させることがなく、様々なドメインにおける LLM の汎用性を維持する。
AWQ は Instruction Tuning された LM やマルチモーダル LM にも適用可能である。

 思ったことGPTQ よりも AWQ の方が量子化後のモデルの性能が高いため、基本的には AWQ を使っていけば良さそう。
VLM について、Language Model がモデルの大部分を占めるため、Vision Encoder は量子化せず、LM の部分のみ量子化しているとのことだった。更なるメモリ削減を狙うのであれば、Vision Encoder の量子化についても考えられると良いのかもしれない。