Zenn
シグマアイテックブログPublicationへの投稿
🖇️

最適化システムにおいてドメイン知識をいかに扱うか

mullchan
2023/12/14に公開
#
アーキテクチャ
#
設計
#
DDD
#
数理最適化
#
ドメイン駆動設計
tech

数理最適化Advent Calender 2023の13日目の記事です。この記事では、数理最適化を含むシステムにおいて問題解決の対象であるドメインの知識をどのように扱うかについて、現時点での私の考えをまとめています。数理最適化またはソフトウェア設計のいずれかを知っている方ですと、読みやすい記事になっているかと思います。

概要

  • ドメインの問題を解決する最適化システムでは、ドメイン知識が必要でありシステムの複雑性を増す要因となりえます。
  • 最適化システムにおいてドメイン知識を適切に扱うための手段として、ソフトウェア設計手法、特にドメイン駆動設計が有効ではないかと考えました。
  • 具体例として配送計画問題を取り上げて、Pythonによる実装例を紹介します。

この記事では、数理最適化を単に「最適化」、数理最適化を用いたシステムを「最適化システム」と呼ぶことにします。

はじめに

はじめに、簡単な自己紹介とこの記事の問いに取り組んでいる経緯をお話します。本題が気になる方は読み飛ばしてもらって結構です。

私は大学の研究室で、量子アニーリングという最適化手法に関する応用研究を企業と共同で行ってきました。その共同研究の対象は配船計画問題で、荷物を船を用いて運ぶ際に効率の良い計画を求める問題でした。配船計画の問題領域は荷物や船、港のバースなど、様々な概念やルールが存在し、当時の自分はこれらの扱いに苦労していました。
現在は株式会社シグマアイにて、最適化技術を用いたソリューションの提供やサービス開発を行っています。特に物流業界の課題に取り組んでいますが、物流業界もやはり複雑なドメインであり、その複雑さがソフトウェアによる課題解決を困難にしうる要因と捉えています。

そこで、概念やルールといったドメイン知識をいかに扱うかという問題に取り組むべく、昨年頃から一般的なソフトウェア開発に関する方法論を学んでいます。最適化システムに関する業務において実践しながら考えたことを、この場で一度共有したいと思います。

導入: 最適化システム

この記事の導入として、最適化問題の概要と最適化システムの構成、システムにおけるドメイン知識について述べます。

最適化問題とは

最適化問題とは、目的関数を最小化(あるいは最大化)するような変数の値を求める問題のことです。目的関数は、例えば事業のKPIやその要素、KPIに相関するような別の指標などが採用されます。また現実の問題では、等式や不等式で記述される制約条件が与えられる場合が多いです。最適化問題は一般的に以下のように表されます。

\min_{\boldsymbol{x}} f(\boldsymbol{x}) \\ \text{subject to} \quad g(\boldsymbol{x}) \leq 0

ここで、\boldsymbol{x}が決定変数で連続値や離散値を取ります。fが目的関数、gを含む不等式が制約条件です。最終的な出力は決定変数の値、それから目的関数の値と制約条件の充足度です。

対象の問題をこのような数理表現(最適化モデル)に落とし込んだ後、この問題を解くための解法(アルゴリズム)を構築します。最適化モデルの特定のクラスに対する汎用的な解法や特定の問題に特化した解法があり、数理最適化やオペレーションズ・リサーチの分野で研究が行われています。

最適化に関するプロジェクトは以下のような流れで進めます。

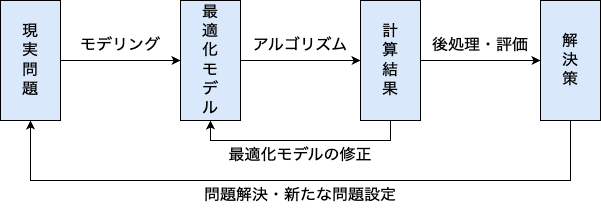
最適化プロジェクトの流れ

このように反復的に開発を進める理由としては、

  • 暗黙的な目的関数・制約条件の明示化
  • 目的関数・制約条件の重み付けの調整
  • 性能向上のためのアルゴリズムの修正

があります。例えば、従来人手で行われていた作業について、その制約条件が担当者しか知らないような現場が存在します。暗黙的な目的関数・制約条件を明示化するために、現時点での問題を解いてみて得られた結果を担当者に確認してもらい、実用において不十分な点を指摘してもらいます。また、目的関数・制約条件の重み付けについても実際に計算しながら調整していきます。要件として質の高い結果が求められるような場合は、アルゴリズム自体の修正も必要となります。

参考ページ:

最適化システム

このような反復を経て最適化によるソリューションの実証実験が概ね完了した後で開発される、本番運用されるシステムついてこの記事では述べていきたいと思います。今回のシステムは、業務管理システムと最適化システムに大きく分かれる構成を想定します。業務管理システムはユーザの操作を直接受け付けて、データを管理し業務を支援するシステムです。最適化システムは最適化技術を用いて、計画業務など業務の一部を代行・支援するシステムです。

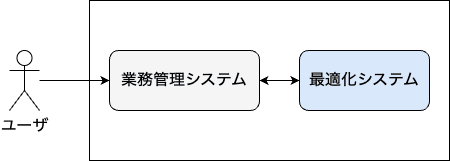
システム構成図

モノリスやマイクロサービスなど、特定のアーキテクチャに限定していない点にご注意ください。ここで重要なのは、業務管理システムと最適化システムで目的が異なる点であり、それを強調するために上のような図を示しました。ただし、必要な計算リソースがこれらのシステムで異なるため、実際はインスタンス等を分けてWeb APIやデータベースを介してやり取りする場合が多いです。

最適化システムでは、以下のようなパイプラインでデータが処理されます。左上の入力データから始まり、右下の計算結果と評価結果を出力して終了です。

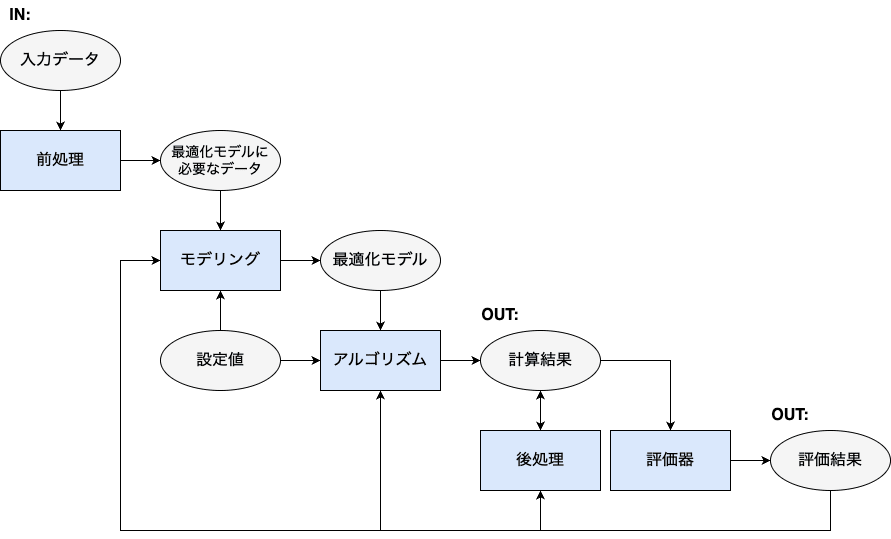
最適化システムにおけるパイプライン

  1. はじめに、入力データ(最適化計算の元となるデータ)を業務管理システムからのHTTPリクエストやデータベースより取得します。
  2. 入力データの前処理として、バリデーションや欠損値の補完などが行われます。後述しますが、最適化特有の前処理を行う必要もあります。
  3. 前処理を通して、最適化計算に必要なデータが抽出されます。これを元に最適化モデルを作成します。
  4. 最適化モデルにアルゴリズムを適用することで最適化計算を実行します。なお、最適化モデルやアルゴリズムに設定値(ハイパーパラメータ)が存在する場合はここで与えます。
  5. 最適化の計算結果について目的関数の値や制約条件の充足度を評価することで、現実の問題を解決するのに十分な結果かどうかを判断します。
  6. より良い計算結果を得るために、評価結果は最適化モデルやアルゴリズムにフィードバックされることもあります。

補足として、最終的な評価では目的関数や制約条件以外の指標も用いられます。現実のすべての要求を最適化計算に反映しようとすると、最適化モデルやアルゴリズムが複雑になり多くの場合で計算が難しくなります。そこで、目的関数や制約条件の優先度を定めて、最適化モデルで考慮しない指標は計算結果のフィルタリングで対応したりします。他には、指標が最適化モデルやアルゴリズムで扱いづらいときに評価だけで済ませるという選択も考えられます。

ドメイン知識とシステムの複雑性

最適化計算には、ドメインに存在する概念やルールといった「ドメイン知識」が必要となります。上記のパイプラインにおいて、ドメイン知識が必要となるのは主に以下の3箇所です。

  1. 入力データの前処理
  2. モデリング(数理モデルの構築)
  3. 計算結果の後処理・評価

パイプラインにおいてドメイン知識が必要な部分

「はじめに」の章でも述べたように、ドメイン知識がソフトウェアを複雑にし、ソフトウェアによる問題解決を難しくする可能性を秘めています。この点について、大変参考にさせていただいている「ドメイン駆動設計は何を解決する手法なのか」という記事を元に説明したいと思います。
最適化にかかわらず、システム開発やサービス開発は利益を上げることを目指します。その目的とは反対に、利益を損なってしまう原因として以下が考えられます。

  • ユーザ満足度の低下による売上減少
  • 保守や機能追加のコスト増大

後の章で紹介するドメイン駆動設計をはじめとするソフトウェア開発の手法は、上記の課題を解決することで、

  • 機能性の向上
  • 変更容易性の向上

を目指します。最適化システムにおいては、特に後者の変更容易性が重要だと考えています。対象の構造やルールが変更された場合、ドメイン知識を含む最適化システムはその変更に対応しなければなりません。また、長期的な視点では最適化システムが導入された結果、対象の状態や問題、人の意識などが経時的に変化する可能性があり、それに合わせて最適化システムもアップデートすることが理想と言えるでしょう。

以降、このような目的を達成するために、最適化システムの設計においてドメイン知識をどのように扱うとよいかを考えていきます。

具体例

以降の内容をより理解するために、ここで最適化問題の具体例を紹介します。

配送計画問題とは

ここでは、代表的な組合せ最適化問題の一つである配送計画問題(Vehicle Routing Problem, VRP)を題材にします。VRPは複数の車両を用いて拠点から顧客に荷物を配送する際に、前もって定めた計画の"良さ"に基づいて、車両がどの顧客を担当するかといった計画を求める問題です。計画の良さは様々考えられますが、今回は効率性向上のために移動コスト(距離や時間)が小さいほど良い計画とします。

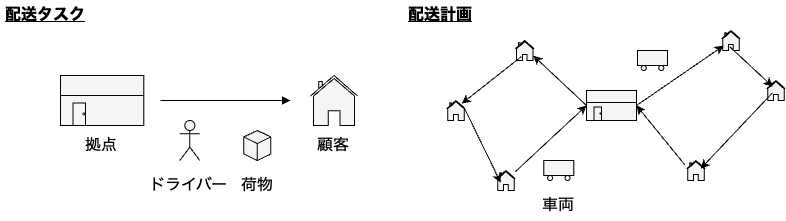
配送計画問題の概要

VRPは様々なバリエーションが研究されており、例えば顧客が希望する時間帯に配送する「時間枠制約」は現実の問題でよく見かける制約条件です。この記事では、車両の容量を考慮する「容量制約」付きのVRPであるCVRP(Capacitated VRP)を取り上げます。また、車両と荷物の出発地である拠点は1箇所のみとします。

定数(最適化モデルに必要なデータ):

  • ノード(顧客と拠点)の集合
  • 車両の集合
  • ノード間の移動コスト(距離や時間など)
  • 顧客の荷物の量(重量など)
  • 車両の容量(最大積載重量など)

決定変数:

  • 各車両がどのノードからどのノードに移動するか

目的関数:

  • 車両の移動コストの総和を最小化する

制約条件:

  • 各顧客には1度のみ訪れる
  • 荷物の総量が車両の容量を超えない
  • 拠点から出発して戻ってくる

CVRPがどのような数式で表されるか興味のある方は、以下をお読みください。

CVRPの定式化の詳細

CVRPの(混合整数)線形計画問題としての定式化は以下のとおりです。

定数:

  • C: 顧客の集合
  • N: ノード(顧客と拠点)の集合
  • V: 車両の集合
  • D_{ij}: ノードiとノードjの移動コスト
  • W_{i}: 顧客iの荷物の量
  • Q_{v}: 車両vの容量

決定変数:

  • x_{ijv} \in \{0,1\}: 車両vがノードiからノードjに移動する場合に1、そうでない場合に0

目的関数:

  • 車両の移動コストの総和を最小化する
\min_{\boldsymbol{x}} \sum_{v \in V} \sum_{i, j \in N} D_{ij} x_{ijv}

制約条件:

  • 各顧客には1度のみ訪れる
\sum_{v \in V} \sum_{j \in N} x_{ijv} = 1, \ \forall i \in C
  • 荷物の総量が車両の容量を超えない
\sum_{i \in C} \sum_{j \in N} W_{i} x_{ijv} \leq Q_{v}, \ \forall v \in V
  • 拠点から出発する
\sum_{j \in N} x_{0,jv} = 1, \ \forall v \in V
  • 拠点に戻ってくる
\sum_{j \in N} x_{i,|C|+1,v} = 1, \ \forall v \in V
  • 各顧客に入る回数と出る回数は同じ
\sum_{i \in N} x_{ikv} = \sum_{j \in N} x_{kjv}, \ \forall k \in C, \forall v \in V

CVRPを選んだ理由としては、例示として問題が単純すぎないためです。ノード間の移動コストは色々な定義が考えられ、何を採用するか、どのように算出するかはドメイン知識と呼んで差し支えないかと思います。この記事では後ほど2種類の距離が登場します。移動コストの他には荷物の量についても、グラムや個数といった種々の単位を扱う場合はロジックの実装が想定されます。
CVRPを選んだもう一つの理由は、次に説明する多段階の解法を説明するためです。

多段階の解法

VRPを解くためのフレームワークの一つに、Cluster-First Route-Secondと呼ばれる多段階の方法があります。これは上記の問題を以下のように2つの部分問題に分けて解きます。

  1. 車両へのタスク割当: タスクを車両に割り当てる
  2. 車両ごとのルーティング: 各車両について、顧客の訪問順序やスケジュールを決める

現実の問題に対する解法は多段階になる場合が少なくありません。最適性が失われる可能性があるにもかかわらず問題を分割する理由としては、以下があげられます。

  • 元の問題が大規模・複雑なため、現実的な時間で求解できない
  • 目的関数が複数存在する
  • 最適解(目的関数が最小となる解)でなくても実用に足る解が得られればよい

まずは非機能要件として現実的な計算時間が求められる場合です。問題を分割することで複雑さが軽減され、問題によっては並列処理が可能となるため、計算速度の向上が期待できます。今回の配送計画問題では、車両に顧客を割り当ててしまうことで、ステップ2は車両ごとに独立の問題となり、並列に計算可能となります。

また、現実の問題は複数の目的関数を持つ多目的最適化問題である場合が非常に多いです。複数の目的関数を同時に扱うとき、それらの重み付け(優先度)を決めなければいけません。比較的簡単な解法として、目的関数が単一の問題に分割し、部分問題を順次解く中で前段の結果に関する制約条件を加えていく方法があります。(参考: 久保先生のポスト)

多段階の解法の利点として、最適化計算とユーザとの協調体験を実現しやすい点にも触れておきたいと思います。計画業務に最適化を適用する場合、事業の状況や環境が時々刻々と変化する中で、計画業務を完全自動化して所望の結果を得ることは容易ではありません。ユーザの受容性の観点からも完全な自動化は避けたいところです。そこでシステム開発においては、ユーザに計算結果の選択や修正を行ってもらうことが有効な対処方法となります。多段階の解法では、それぞれの問題で得られた計算結果をいったんユーザに委ねながら計算を進めることで、より現実に即した結果を得ることができるでしょう。

しかし、このとき一連の処理に評価に関するドメイン知識が混ざってしまい、システムの複雑さを増す要因になります。例えば、シフト作成など人が関わる最適化問題の場合、労務ルールに関する評価が欠かせません。そのようなルールは追加・変更されるものであり、最適化システムもそれに対応するために改修する必要があるため、一般的なシステムと同様に変更容易性が重要です。

先の章では、上記の解法における「車両へのタスク割当」問題について、ドメイン知識を適切に扱うための実装例を紹介します。

手段: ソフトウェア設計手法

本題に入る前に、ドメイン知識の取り扱いへの処方箋としてソフトウェア設計手法を紹介します。

ドメイン駆動設計とは

既にドメインという言葉を多用している通り、最適化システムではドメインの知識に注意を払うべきです。そこで、ソフトウェア設計手法の一つであるドメイン駆動設計に基づいて、ドメイン知識の扱い方を考えていきます。ドメイン駆動設計は、ソフトウェアで問題を解決したい対象領域であるドメインをモデリングすることで、ソフトウェアの価値を高める手法です。

参考: ドメイン駆動設計は何を解決しようとしているのか

ドメイン駆動設計の詳細については、この記事の最後に記載したとおり多くの書籍が出ていますのでそちらをご参照ください。

ソフトウェアアーキテクチャ

ソフトウェアアーキテクチャについては、ここではオニオンアーキテクチャを採用します。理由としては、アーキテクチャにおける最適化モデルの位置づけを明確にする上で、構成の具体度が適度であると判断したためです。

オニオンアーキテクチャにおける最適化モデルの位置づけ

アーキテクチャを考えることで責務(関心)を分離し、疎結合かつ高凝集を目指します。オニオンアーキテクチャにおける各層の責務は以下のとおりです。

  • ドメイン層: ドメイン知識の表現
  • ユースケース層(アプリケーション層): ユースケースの実現
  • プレゼンテーション層: クライアントとの入出力
  • インフラ層: データベースや外部システムとの入出力

制御の流れと依存関係が分離されることもポイントです。この図では上の層が下の層に依存してよいですが、その逆は許容しません。ドメイン層は上位の位置づけで他の要素に依存したくないため、依存性逆転の原則によって制御と依存関係の向きを逆にします。具体例は以降の章で登場します。

参考: 世界一わかりやすいClean Architecture

次の章ではオニオンアーキテクチャのうち、ドメイン層とインフラ層に属するオブジェクトについて触れます。

応用: 最適化システムにおけるドメイン知識の扱い方

この章では前述のタスク割当問題について、入力データの前処理、最適化モデルの構築、計算結果の後処理・評価におけるドメイン知識の扱い方を実装例とともに紹介します。

入力データの前処理

入力データの前処理の目的は、最適化に必要なデータを使える形式や状態で抽出することです。前処理の種類は以下のとおりです。

  • データのバリデーションや欠損データの処理など、一般的なデータ分析で見られる前処理
  • 最適化のための前処理

最適化のための前処理には、問題の規模や複雑さを抑えることで計算しやすくするものがあります。配送計画問題の場合は、地理的に近い顧客のタスクをまとめて1つのタスクに変換することで、最適化問題のサイズ(決定変数の数)を小さくすることができます。最適化のための前処理については、以下の動画が参考になるのでぜひご覧ください。

参考: 実際の最適化問題に対する前処理は，機械学習やデータサイエンスの前処理とは異なり，アートであるというお話 - YouTube

CVRPに対するタスク割当問題に登場する概念を、ドメインモデル図を用いて整理してみました。ドメインモデル図の描き方については、「簡単にできるDDDのモデリング - ドメイン駆動設計」を参考にしています。

配送計画問題のドメインモデル

ここで、タスク割当(TaskAssignment)オブジェクトを除いてすべて入力データで、タスク割当オブジェクトはタスク割当問題の計算結果です。また、自分はドメインモデル図に目的関数や制約条件の情報も記載するようにしています。

これらのオブジェクトをいくつかの設計パターンを用いて実装していきます。Pythonによる実装方法については、「Python で学ぶ実践的なドメイン駆動設計とレイヤードアーキテクチャ / DDD and Onion Architecture in Python」を一部参考にしています。

値オブジェクト

値オブジェクトは、システム固有の値を表現するオブジェクトです。値オブジェクトの性質としては、不変性、交換性、等価性があります。
ここでは、荷物の重量を値オブジェクトとして実装してみます。

@dataclasses.dataclass(frozen=True)
class ItemWeight:
    value: float

    def __post_init__(self):
        if self.value < 0:
            raise ValueError("Item weight must be positive")

    def __add__(self, obj: object) -> ItemWeight:
        if not isinstance(obj, ItemWeight):
            raise ValueError("Only ItemWeight can be added to ItemWeight")
        return ItemWeight(self.value + obj.value)

値オブジェクトの基本となる性質はdataclassデコレータを用いて実現できます。重量は0以上のため、__post_init__メソッドでバリデーションを行い不正な値が存在しないようにします。また、__add__メソッドで重量どうしの加算を記述しているように、値オブジェクトのふるまいを定義することができます。
他には、車両番号が"hoge-123-1"のように何かしらの構成を持つ場合、プリミティブな値では表現力に欠けるため値オブジェクトを採用するのがよいでしょう。

エンティティ

エンティティは可変性、同一性を持つドメインオブジェクトです。同一性とは、属性値ではなく識別子によってオブジェクトが同一かどうかが決まる性質のことです。そのため、値オブジェクトとは異なり、属性値が同じであってもエンティティは区別されることになります。エンティティの例としては、人間が分かりやすいと思います。人間の属性として名前を考えたときに、ある2人が同姓同名であっても互いに異なる存在です。
VRPにおけるエンティティの中で、タスクエンティティの実装例を紹介します。

@dataclasses.dataclass
class Task:
    id: TaskId
    items: Items
    origin: NodeId
    destination: NodeId

    def __eq__(self, obj: object) -> bool:
        if isinstance(obj, Task):
            return self.id == obj.id
        return False

    @property
    def total_item_weight(self) -> ItemWeight:
        return self.items.total_weight

    @staticmethod
    def create(
        task_id: TaskId, items: Items, origin: NodeId, destination: NodeId
    ) -> Task:
        if items.number < 1:
            raise ValueError("At least one item must exist")
        if origin == destination:
            raise ValueError("The origin and destination must be different")
        for item in items:
            if item.customer.id != destination:
                raise ValueError(f"Item owner and destination must match: {item.id}")

        return Task(id=task_id, items=items, origin=origin, destination=destination)

まずは、識別子TaskIdを属性として持っていることに注目してください。__eq__メソッドでこの識別子を比べることで、2つのタスクエンティティが同じかどうかを判定します。タスクに関するロジックとして、後の最適化モデルで必要となる荷物の総重量を計算する処理が必要です。これをタスクエンティティに記述することで(total_item_weightメソッド)、ロジックの点在を防ぐことができます。

エンティティについても、不正な値が存在しないようにまずはオブジェクトの生成段階で値のバリデーションを行います。タスクエンティティには上のドメインモデル図に記した通り3つの"条件"があり、createメソッドにその判定を記述しています。
ここまでの内容だけでは、単なるデータクラスと大差ないと思われた方がいるかと思います。実際その通りで、ドメイン知識の表現方法・扱い方として説明していないことがあります。それは、タスクエンティティの生成メソッドに記述したような「不変条件」です。不変条件の詳細と実装例については、「計算結果の後処理・評価」の節で述べたいと思います。

ファーストクラスコレクションとしてのItemsクラスの実装

Itemsクラスは複数のItemエンティティを扱うことに特化したクラスです。通常の配列のような操作に加えて、特定のオブジェクトに関する処理が実装されたクラスで、ファーストクラスコレクションと呼ばれています。例えば、複数の荷物の総重量を計算する処理はItemsに記述します。

class Items:
    def __init__(self, items: list[Item]):
        self._items = {item.id: item for item in item.values()}

    @property
    def total_weight(self) -> ItemWeight:
        return ItemWeight(
            sum(item.weight.value for item in self._items.values())
        )

    def add(self, item: Item):
        if item.id in self._items.keys():
            raise ValueError(f"Item already exists: {item.id}")
        self._items[item.id] = item

リポジトリ

リポジトリはデータの永続化や再構成を行うためのオブジェクトです。ここでは入力データの構成において、車両エンティティをRDBから再構成するリポジトリの実装例を示します。

from sqlalchemy.orm.exc import NotResultFound
from sqlalchemy.orm.session import Session

class VehicleRepository(abc.ABC):
    @abc.abstractmethod
    def find_by_id(self, vehicle_id: VehicleId) -> Vehicle | None:
        pass

class RDBVehicleRepository(VehicleRepository):
    def __init__(self, session: Session):
        self._session = session

    def find_by_id(self, vehicle_id: VehicleId) -> Vehicle | None:
        try:
            vehicle_dto = self._session.query(RDBVehicleDTO).filter_by(
                id=vehicle_id.value
            ).one()
        except NoResultFound:
            return
        return vehicle_dto.to_entity()

車両リポジトリの抽象クラスVehicleRepositoryはドメイン層、SQLAlchemyを用いた具体クラスRDBVehicleRepositoryはインフラ層に置きます。こうすることで、車両オブジェクトの再構成というドメイン知識が、特定の外部APIに依存しないようにできます。これが前に触れた、依存性逆転の原則です。

リポジトリのオンメモリ実装

リポジトリを抽象クラスと具体クラスに分けたら、オンメモリのモック実装を用意しましょう。この実装は単体テスト時に役立ったり、ドメイン駆動設計の進め方として先にドメインモデルの実装に集中できるようになります。

class OnMemoryVehicleRepository(VehicleRepository):
    def __init__(self, vehicles: list[Vehicle]):
        self._vehicles = {vehicle.id: vehicle for vehicle in vehicles}

    def find_by_id(self, vehicle_id: VehicleId) -> Vehicle | None:
        return self._vehicles.get(vehicle_id)

なお、ドメイン駆動設計には集約という考え方があり、これは整合性を持つオブジェクトの集合です。ドメイン駆動設計において非常に大切なのですが、境界付けられたコンテキストなど他の概念が関連し、話が発散しまうためこの記事では割愛します。

また、外部APIを利用してドメインオブジェクトを構成する場合も、リポジトリになるかと思います。配送計画問題では、次の外部APIを利用することが考えられます。

  • ジオコーディング(住所から緯度経度への変換)
  • 地図上での2地点間の経路探索

ジオコーディングにはGoogle Maps APIが利用できます。車両リポジトリと同様、抽象クラスと具体クラスをそれぞれドメイン層とインフラ層に配置します。

import googlemaps

class GeocodingRepository(abc.ABC):
    @abc.abstractmethod
    def execute(self, address: Address) -> Location:
        pass

class GoogleMapsGeocodingRepository(GeocodingRepository):
    def __init__(self, api_key: str):
        self._api_key = api_key

    def execute(self, address: Address) -> Location:
        gmaps = googlemaps.Client(key=self._api_key)
        response = gmaps.geocode(address)
        if len(response) == 0:
            raise Exception(f"No location found for address: {address}")

        location = response[0]["geometry"]["location"]
        return Location(location["lat"], location["lng"])

経路探索についてもGoogle Maps APIが使えるので、ジオコーディングの実装クラスと同様になります。ちなみに、他の実装方法としてはOSRM(Open Street Routing Machine)がおすすめです。OSRMはあらかじめローカルにデータをダウンロードすることで、オフラインでかつ高速な経路探索を実現します。

ちなみに、ジオコーディングは最適化システムではなく業務管理システム側で行ってもよいと思います。ここでは、緯度経度の情報が最適化計算でのみ必要という仮定の元で、最適化システム側で行う形をとっています。

ファクトリ

ファクトリは、ドメインオブジェクトを生成するためのオブジェクトです。生成過程が単純な場合は、ドメインオブジェクト自身が生成メソッドを持てばよいのですが、複雑な場合には専用のオブジェクトを用意します。ドメインオブジェクトの生成過程がドメイン知識と捉えられる場合、ファクトリはドメイン層に属するのが自然でしょう。
配送計画問題、特に前述した多段階の解法において、各段階で2種類の距離(移動コスト)を利用する場合を考えます。前段では任意の2地点間の距離が必要なため、計算量の観点からユークリッド距離を採用することにします。後段の車両のルーティングでは地図上の経路を計算して得られる距離を用います。

class DistanceFactory(abc.ABC):
    @abc.abstractmethod
    def create(self, origin: Node, end: Node) -> Distance:
        pass

class EuclideanDistanceFactory(DistanceFactory):
    def create(self, origin: Node, end: Node) -> Distance:
        distance = np.sqrt(
            (origin.latitude - end.latitude) ** 2
            + (origin.longitude - end.longitude) ** 2
        )
        return Distance(distance)

class RouteDistanceFactory(DistanceFactory):
    def __init__(self, route_search: RouteSearch):
        self._route_search = route_search

    def create(self, origin: Node, end: Node) -> Distance:
        route = self._route_search.execute(origin, end)
        return route.distance

最適化モデルの構築

前節で用意した入力データから、最適化モデルに必要なデータを抽出します。CVRPでは、入力データから算出するのは次の2つのオブジェクトです。

  • ノード間の移動コスト(距離): Distance (DistanceFactoryより取得)
  • 荷物の総重量: ItemWeight (Task.total_item_weightより取得)

抽出したデータのドメインオブジェクトから、最適化モデルを構築します。HTTPやデータベースを含むデータやオブジェクトの流れは以下のとおりです。左上のHTTPリクエストから始まり、反時計回りに左下まで進みます。参考までに、各要素に括弧書きでPythonのライブラリの使用例を載せています。

ドメインモデルと最適化モデルの分離

最適化計算はそれなりに時間がかかるため、非同期処理を採用する場合が多いです。そのため上の図とは少し異なり、リクエストデータを受け取った段階などでHTTPレスポンスをクライアントに返した後、バックグラウンドで後続の処理を実行したりします。

この図を見て分かる通り、最適化モデルはドメインオブジェクトを用いてドメインオブジェクトを生成することから、ファクトリ、あるいはドメインサービスと捉えることができると思います。ドメインサービスとは、ドメインオブジェクトに関する何かしらの処理を実行するクラスです。ドメインサービスを採用するのは、特定の値オブジェクトやエンティティに記述するのが不自然な処理の場合です。注意点として、ドメインサービスが乱用されると、データとロジックが離れてしまいロジックが点在してしまいます。最適化モデルは複数のオブジェクトを扱う点からも、ドメインサービスとして考えるのが良いと思います。

次に、最適化モデルの実装例を見てみましょう。以下はタスク割当問題のコードです。

class TaskAssignmentProblem(abc.ABC):
    def __init__(self, tasks: Tasks, vehicles: Vehicles):
        self._tasks = tasks
        self._vehicles = vehicles
        self.set_variables(tasks, vehicles)

    @abc.abstractmethod
    def set_variables(self, tasks: Tasks, vehicles: Vehicles):
        pass

    @abc.abstractmethod
    def add_travel_cost_objective(
        self, travel_costs: dict[tuple[TaskId, TaskId], Distance]
    ):
        pass

    @abc.abstractmethod
    def add_vehicle_capacity_constraint(
        self,
        item_weights: dict[TaskId, ItemWeight],
        vehicle_capacities: dict[VehicleId, VehicleCapacity],
    ):
        pass

    @abc.abstractmethod
    def add_task_assignment_constraint(self):
        pass

タスク割当問題がどのような目的関数と制約条件からなるか、どのようなデータが必要かが一目で分かります。コードのドキュメント性が高い状態といえます。ただし、決定変数は最適化モデルの種類(具体クラス)によって少し異なるため、抽象クラスには明示できていません。この点は最適化モデルのクラス設計をもう少し工夫すると解決できるのですが、その話は別の機会にしたいと思います。

コンストラクタでタスクオブジェクトと車両オブジェクトを受け取った後、set_variablesメソッドで決定変数を用意します。add_から始まるメソッドはこの問題を構成する目的関数と制約条件を設定するためのものです。
このクラスはabc.ABCを継承している通り、抽象クラスです。以下の情報がインターフェイスとして記述されています。

  • 問題がどのような決定変数、目的関数、制約条件から構成されるか
  • 目的関数、制約条件にどのようなデータが必要か

最適化システムにおいて、これらはドメイン知識の一つとして捉えて差し支えないでしょう。ドメイン知識を有する最適化モデルの抽象クラスはドメイン層に置くことにします。
一方で、最適化モデルは多くの場合、モデラーと呼ばれる外部ライブラリを用いて実装されます。PuLPというライブラリを用いた実装クラスはこちらです。

PuLPを用いたタスク割当問題の実装クラス
import pulp

class PulpTaskAssignmentProblem(TaskAssignmentProblem):
    def set_variables(self, tasks: Tasks, vehicles: Vehicles):
        self._interact_variables = {
            (task1, task2): pulp.LpVariable(f"interact_{task1}_{task2}", cat="Binary")
            for task1, task2 in itertools.combinations(tasks, 2)
        }
        self._assignment_variables = {
            (task.id, vehicle.id): pulp.LpVariable(f"assignment_{task.id}_{vehicle.id}", cat="Binary")
            for task in tasks for vehicle in vehicles
        }

    def add_travel_cost_objective(
        self, travel_costs: dict[tuple[TaskId, TaskId], Distance]
    ):
        objective = pulp.lpSum(
            travel_costs[task1, task2].value
            * self._interact_variables[task1, vehicle]
            * self._interact_variables[task2, vehicle]
            for task1, task2 in itertools.combinations(self._tasks, 2)
            for vehicle in self._vehicles
        )
        self.add_objective(objective, label="travel_cost")

    def add_vehicle_capacity_constraint(
        self,
        item_weights: dict[TaskId, ItemWeight],
        vehicle_capacities: dict[VehicleId, VehicleCapacity],
    ):
        constraints = []
        for vehicle in self._vehicles:
            total_item_weight = pulp.lpSum(
                item_weights[task] * self._assignment_variables[task, vehicle]
                for task in self._tasks
            )
            constraints.append(total_item_weight <= vehicle_capacities[vehicle])

        self.add_constraint(constraints, label="vehicle_capacity")

    def add_task_assignment_constraint(self):
        constraints = []
        for task in self._tasks:
            num_assigned_vehicles = pulp.lpSum(
                self._assignment_variables[task, vehicle]
                for vehicle in self._vehicles
            )
            constraints.append(num_assigned_vehicles == 1)

        self.add_constraint(constraints, label="task_assignment")

    def add_same_assignment_constraint(self):
        constraints = []
        for task1, task2 in itertools.combinations(self._tasks, 2):
            for vehicle in self._vehicles:
                constraints.append(
                    self._assignment_variables[task1, vehicle]
                    + self._assignment_variables[task2, vehicle]
                    <= self._interact_variables[task1, task2] + 1
                )

        self.add_constraint(constraints, label="same_assignment")

そこで下の図のように、最適化モデルの実装クラスはインフラ層に配置してみます。ただし、外部ライブラリに依存せず、かつドメイン知識を使うような実装クラスはドメイン層に置くのがよいかと思います。

最適化モデルの切り替え

最適化の専門的な話になりますが、一つの最適化問題に対して複数の定式化(数理表現)が考えられます。タスク割当問題については、上で示したような線形計画問題(Linear Programming, LP)と二次計画問題(Quadratic Programming, QP)などがあります。さらに一種類の定式化に対しても複数の実装方法(ライブラリ)が存在しますが、定式化と実装を分けることは技術的に容易でなく開発コストが効果に見合わないため、今のところ1つのクラスに両者をまとめる方針をとっています。

また、最適化モデルの抽象クラスを設けることでモック実装が可能となり、リポジトリと同様にテストがしやすくなります。モデラーを使わずに単に必要なデータを受け取るだけの実装クラスを作成した上で、例えばランダムサンプリングなどの簡単なアルゴリズムを適用します。ランダムサンプリングでは目的関数や制約条件を完全に考慮できないので、目的関数の値や制約条件の充足度をもとにした計算結果のフィルタリングが必須であり、次節で述べる計算結果の評価を開発の初期に自然な流れで実装することになるため、個人的におすすめです。

計算結果の後処理・評価

前節で述べた最適化モデルとアルゴリズムから得られる計算結果、そして計算結果の評価もドメイン知識であると考えています。この節では、タスク割当問題の計算結果の後処理と評価について説明します。

計算結果の後処理

タスク割当問題の計算結果であるタスク割当オブジェクトは、以下のようなコードになります。

class TaskAssignment:
    def __init__(self, vehicle_tasks: dict[VechileId, list[TaskId]]):
        if not self.is_valid_assignment(vehicle_tasks):
            raise ValueError("Only one vehicle can be assigned to a task")

        self._vehicle_tasks = collection.defaultdict(list)
        self._vehicle_tasks.update(vehicle_tasks)

    @staticmethod
    def is_valid_assignment(vehicle_tasks: dict[VechileId, list[TaskId]]) -> bool:
        task_counts = collections.Counter(
            [task_id for task_ids in vehicle_tasks.values() for task_id in task_ids]
        )
        return all(count == 1 for count in task_counts.values())

    @property
    def vehicles(self) -> list[VehicleId]:
        return list(self._vehicle_tasks.keys())

    @property
    def tasks(self) -> list[TaskId]:
        return list(
            {
                task_id for task_ids in self._vehicle_tasks.values()
                for task_id in task_ids
            }
        )

    @property
    def vehicle_tasks(self) -> dict[VehicleId, list[TaskId]]:
        return dict(self._vehicle_tasks)

    @property
    def task_vehicles(self) -> dict[TaskId, list[VehicleId]]:
        task_vehicles = collections.defaultdict(list)
        for vehicle_id, task_ids in self._vehicle_tasks.items():
            for task_id in task_ids:
                task_vehicles[task_id].append(vehicle_id)
        return dict(task_vehicles)

    def reassign(self, task_id: TaskId, vehicle_id: VehicleId):
        vehicle_id_assigned = self.task_vehicles.get(task_id)
        if vehicle_id_assigned is None:
            raise ValueError(f"Task not found: {task_id}")

        self._vehicle_tasks[vehicke_id_assigned].remove(task_id)
        self._vehicle_tasks[vehicle_id].append(task_id)

ここで、エンティティのところで触れた「不変条件」について詳細を述べます。「モデルでドメイン知識を表現するとは何か[DDD]」では、不変条件は「モデルが有効である期間中、常に一貫している必要のある状態のこと」と定義されています。
タスク割当は次の不変条件を満たす必要があります。

  • 各タスクが1台の車両のみに割り当たっている

この条件を満たすかチェックするためにis_valid_assignmentメソッドを用意し、コンストラクタで呼ぶことで生成時の条件を確認しています。
ところで、最適化のパイプラインにあるように計算結果は後処理が行われます。タスク割当オブジェクトの後処理として考えられるのは、例えば車両の容量に関する制約条件を満たしていないときに、あるタスクを別の車両に再度割り当てる処理です。このような処理において、不変条件を満たしながらタスクを割り当て直す必要があります。上の実装例では、reassignメソッドでタスクの再割当処理が記述されており、不変条件を必ず満たすような操作となっています。

計算結果の評価

最適化の計算結果は、パイプラインにおけるいくつかの部分で評価されます。

  • アルゴリズムの実行途中
  • アルゴリズムの実行後
  • 多段階の解法における各段階の後

途中で評価が必要なアルゴリズムにメタ戦略があります。メタ戦略とは、はじめに初期解を用意し、暫定解を変更し解を評価することを繰り返しながらより良い解を探索する手法の総称です。その一つに重み付き局所探索法があり、例えばCodable Model Optimizerというライブラリでは目的関数や制約条件をPythonのコードで定義することができるため、エンジニアの方でも気軽に利用することができるかと思います。
また、評価の計算式が最適化モデルの目的関数として表しづらいときに、別のモデルを代わりに利用する方法があります。代理モデルを用いて得られた計算結果は元の計算式によって評価され、その評価値をもとに繰り返し計算が行われます。
アルゴリズムの実行後や各段階の後における評価結果は、計算結果の修正や選択で参照されます。

ドメインオブジェクトの評価は単純なものであればメソッドとして定義されますが、計算結果のオブジェクトの評価は複雑な場合が多いです。複雑な評価処理は専用のクラスに記述するのがよいでしょう。このような実装パターンは仕様と呼ばれています。参考までに、『ドメイン駆動設計入門』の第13章「仕様」にてオブジェクトの評価について述べられています。

以下のコードは、計算結果に対して目的関数の値を計算するクラスです。ここでは、あえて最適化モデルで直接考慮していない車両の積載率を計算するクラスを実装してみます。

class BaseObjective(abc.ABC):
    @abc.abstractmethod
    def values(self, *args) -> dict[typing.Hashable, float]:
        pass

    @abc.abstractmethod
    def total_value(self, *args) -> float:
        pass

class LoadingRateObjective(BaseObjective):
    def __init__(self, tasks: Tasks, vehicles: Vehicles):
        self._tasks = tasks
        self._vehicles = vehicles

    def values(self, task_assignment: TaskAssignment) -> dict[VehicleId, float]:
        loading_rates = {}
        for vehicle_id, task_ids in task_assignment.vehicle_tasks.items():
            vehicle = vehicles.get(vehicle_id)
            tasks = self._tasks.get_all(task_ids)
            loading_rates[vehicle.id] = tasks.total_item_weight.value / vehicle.capacity.value
        return loading_rates

    def total_value(self, task_assignment: TaskAssignment) -> float:
        loading_rates = self.values(task_assignment)
        return sum(loading_rates.values()) / len(loading_rates)

次に、制約条件の充足度を計算するクラスの例として、車両の容量に関する制約条件を評価するクラスのコードを紹介します。

class BaseConstraint(abc.ABC):
    @abc.abstractmethod
    def satisfications(self, *args) -> dict[typing.Hashable, float]:
        pass

    @abc.abstractmethod
    def total_satisfication(self, *args) -> float:
        pass

    @abc.abstractmethod
    def is_satisfied(self, *args) -> dict[typing.Hashable, bool]:
        pass

    @abc.abstractmethod
    def is_satisfied_totally(self, *args) -> bool:
        pass

class VehicleCapacityConstraint(BaseConstraint):
    def __init__(self, tasks: Tasks, vehicles: Vehicles):
        self._tasks = tasks
        self._vehicles = vehicles

    def satisfications(self, task_assignment: TaskAssignment) -> dict[VehicleId, float]:
        satisfications = {}
        for vehicle_id, task_ids in task_assignment.vehicle_tasks.items():
            tasks = Tasks()
            for task_id in task_ids:
                tasks.add(self._tasks.get(task_id))

            vehicle = self._vehicles.get(vehicle_id)
            satisfications[vehicle_id] = max(
                0.0, tasks.total_item_weight.value - vehicle.weight_capacity.value
            )

        return satisfications

    def total_satisfication(self, task_assignment: TaskAssignment) -> float:
        return sum(self.satisfications(task_assignment).values())

    def is_satisfied(self, task_assignment: TaskAssignment) -> dict[VehicleId, bool]:
        return {
            vehicle_id: satisfication == 0.0
            for vehicle_id, satisfication in self.satisfications(task_assignment).items()
        }

    def is_satisfied_totally(self, task_assignment: TaskAssignment) -> bool:
        return all(self.is_satisfied(task_assignment).values())

satisficationsメソッドで制約条件の充足度(違反度)をfloat型の数値として求めています。制約条件の充足度は最適化モデルやアルゴリズムへフィードバックし、反復的に計算する場合があるため、その際にこのメソッドが使えます。その値を元に、is_satisfiedメソッドで荷物の総重量が車両の容量を超えるか否かを判定しています。

補足として、計算結果の評価では上の例のように、常にドメインオブジェクトを使うべきとは限りません。というのも、アルゴリズムが直接出力する計算結果がプリミティブな値のとき、値オブジェクトやエンティティへの変換が計算のオーバーヘッドになってしまいます。特に、実行途中で解を評価するアルゴリズムの場合は計算速度やメモリ使用量が優先され、プリミティブな値の計算結果をそのまま評価するクラスや関数を実装することになります。

考察: 最適化システムにおけるドメイン駆動設計の必要性

この記事の問いに対する手段としてドメイン駆動設計を紹介し、実装例を示すことで有効性を確認してきました。
ところで、ドメイン駆動設計は最適化システムの開発において常に必要となるのでしょうか。実際、最適化システムで扱うドメイン知識がそこまで複雑でない場合もあります。例えば、概念は多くてもロジックが少なかったり単純な時は、素直にデータモデリングに注力するべきでしょう。

最適化のプロジェクトにおいて、どの段階からドメイン駆動設計を始めるとよいかも悩ましいところです。設計や開発に慣れていないメンバーがチームにいる場合は育成する時間がかかるため、開始時期を慎重に検討する必要があります。その点を留意した上で、私は実証実験の段階からドメインモデリングやドメインモデルの実装に着手することがあります。その理由として、問題解決に足る最適化モデルやアルゴリズムを構築するためには、検証段階からドメインの深い理解を目指すべきであり、ドメイン駆動設計の手法が有効であると考えているからです。ドメインモデルのインクリメンタルな開発は開発初期の試行錯誤に調和すると実感しています。

ということで、ドメイン駆動設計が必要かどうかは、対象の問題やプロジェクトの状況などに応じて考えることに尽きると思います。また、部分的な導入であったとしても、費用対効果があるのであればアリというのが個人的な考えです。

まとめ

この記事では、最適化システムの設計の観点の一つとして、ドメイン知識の取り扱いについて述べました。長文になってしまいましたが、これ以外にも最適化システムの構築に関して色々な観点で考えていることがあるので、いずれZennのBooks機能などを利用して体系的に整理したいと思っています。

今回はドメイン駆動設計でいうところの戦術面の話でしたが、戦略面の話も最適化のプロジェクトに通ずる部分が非常に大きいと考えています。コアドメインや境界付けられたコンテキストの定義は、最適化技術で挑む問題領域を決めるのに有効です。ユビキタス言語の策定やドメインモデリングはドメインエキスパートとの良いコミュニケーションを実現し、ドメインを深く理解するのに役立ち、最適化によるソリューションを現場に即したものに近づけていきます。今後また記事を書く機会がありましたら、戦略面の話についても私なりの考えをまとめたいと思います。

ここまで述べてきたとおり、最適化システムは複雑なドメインを対象とする場合があり、本番運用されるシステムにおいて設計や開発、運用などの方法論が欠かせません。最適化システムに特化したソフトウェア開発の議論が重要なところですが、自分が認知している範囲ではそのような議論はオープンに行われていないように思います。今後、そのような情報発信やコミュニティの形成が行われていけばよいなと考えています。この記事を含め自分の発信がその一助となれば幸いです。

何か気になる点がありましたら、お気軽にコメントをもらえると嬉しいです。
ここまで読んでくださり、どうもありがとうございました。

参考書籍

シグマアイテックブログ
シグマアイテックブログPublication

株式会社シグマアイのテックブログです！研究開発やソフトウェア開発に関する取り組みやTipsをお届けしていきます。

Discussion