ABC377-E の帰納法による証明
本記事はABC377-E (Permuate K times 2)の解説で説明されている
求める答えは
です。 (P_i^{2^k})_i
の帰納法による証明です。
サンプル1において、
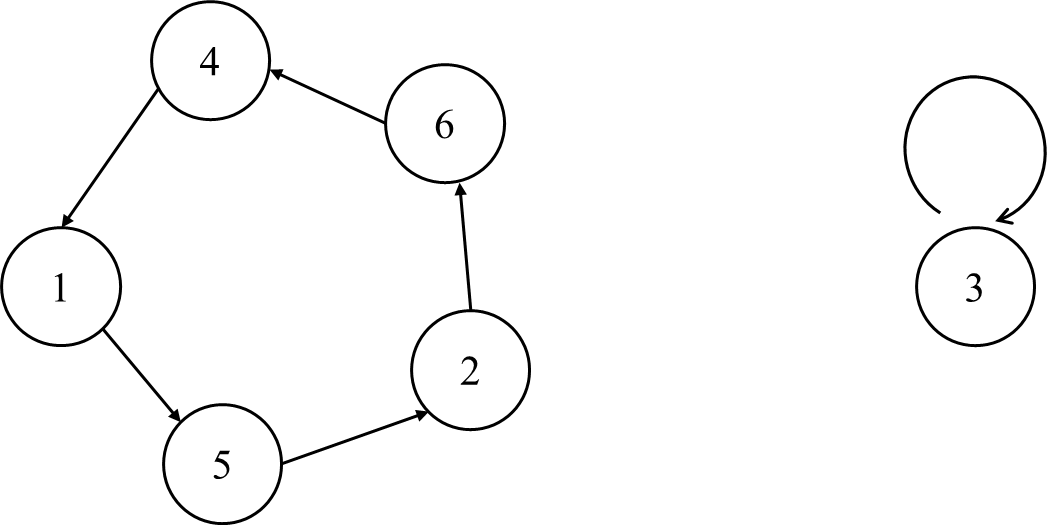
たとえば、
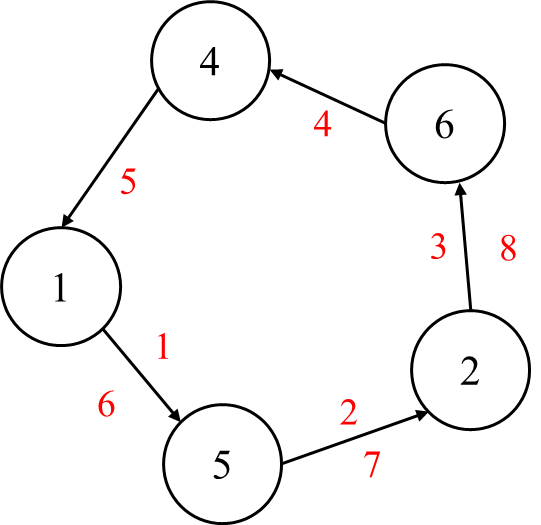
-
K=0
K = 0
構築したグラフの定義から、頂点番号i 2^0 = 1 P_i -
K = k K = k+1
解説の操作で得られるグラフの連結成分が、l, m 1 \le l, m \le N k
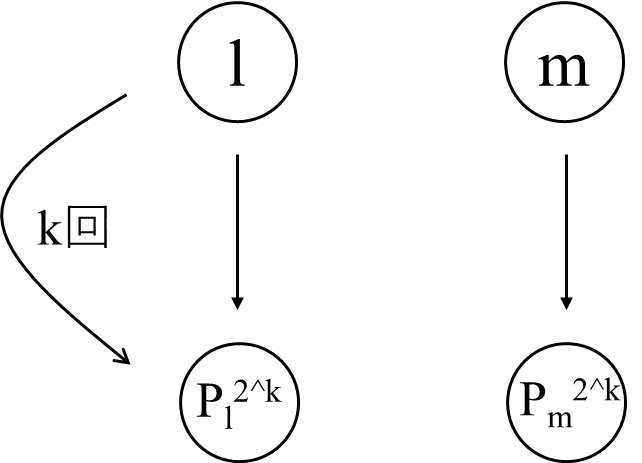
ここで、例えばP_l^{2^k} = m k+1 l k m P_m^{2^k}
帰納法の仮定から、l 2^k P_l^{2^k} = m m 2^k P_m^{2^k} l P_m^{2^k}
2^k + 2^k = 2^{k+1}
となり、頂点l k+1 K = k+1
1, 2より、
求める答えは
(P_i^{2^k})_i
であることを示すことができました。
Discussion