確率密度関数
ガンマ分布の確率密度関数は以下で表される
\begin{align*}
&f(x|\alpha, \beta) =
\frac{1}{\beta^\alpha \Gamma{(\alpha)}}
x^{\alpha-1} e^{-\frac{x}{\beta}} \quad \text{if}\quad 0<x, \quad f(x|\alpha, \beta)=0 \quad \text{otherwise}
\\
&\text{Where,}\quad \Gamma{(\alpha)}=\int_0^\infty x^{\alpha-1} e^{-x} dx,\;0<\alpha
\end{align*}
可視化
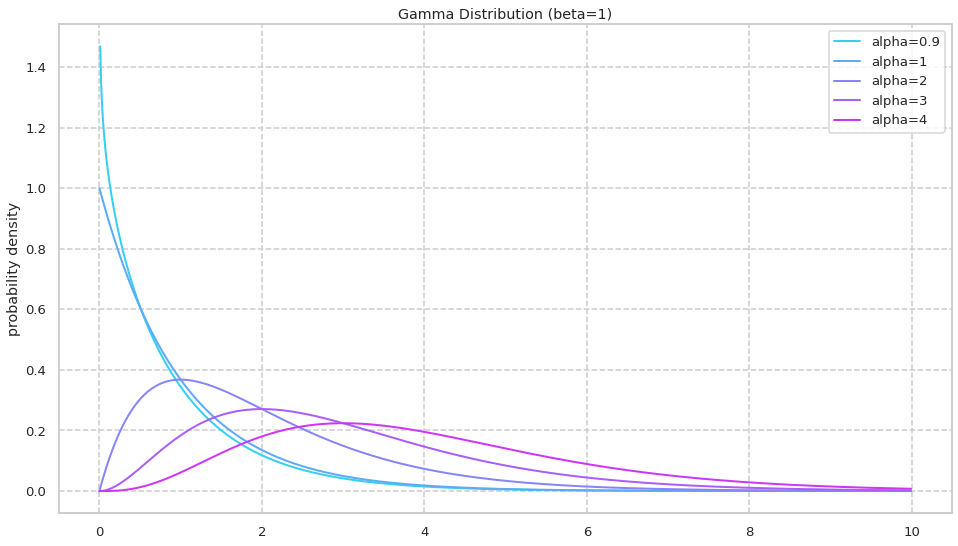
01: \alphaを変化させたときのガンマ分布
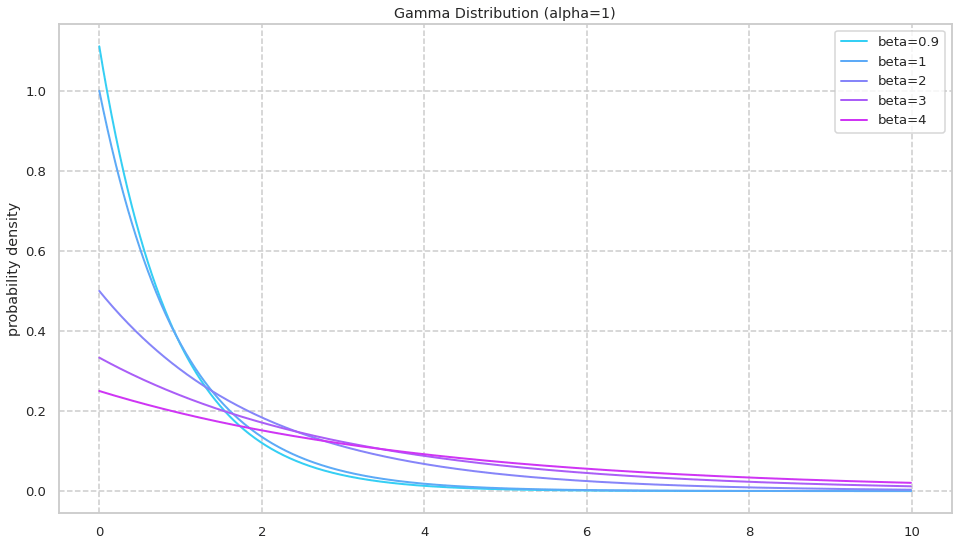
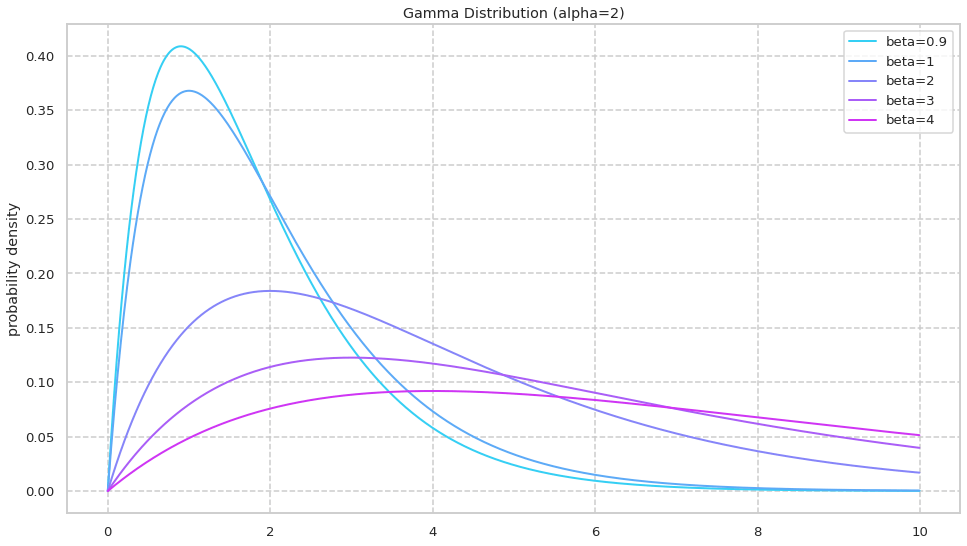
02: \betaを変化させたときのガンマ分布
画像を生成するコード
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import gamma
x = np.arange(0, 10, 0.01)
beta = 1
ys = []
for alpha in [0.9,1,2,3,4]:
y = [
gamma.pdf(
x_,
a=alpha,
scale=beta,
loc=0
)
for x_ in x
]
ys.append(y)
sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 2})
sns.set_palette("cool", 5, 0.9)
fig=plt.figure(figsize=(16,9))
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Gamma Distribution (beta=1)')
ax1.set_ylabel('probability density')
for y in ys:
ax1.plot(x,y)
ax1.legend(['alpha=0.9','alpha=1','alpha=2','alpha=3','alpha=4'])
plt.show()
Gamma関数の公式
\Gamma{(\cdot )} だが, 以下の特徴がある.
\Gamma(\alpha)=\int_{0}^{\infty} t^{\alpha-1} e^{-t} d t
等式
ガンマ関数について以下が成り立つ.
\Gamma(\alpha)=(\alpha-1) \Gamma(\alpha)
証明
\begin{align*}
\Gamma(\alpha) & =\int_{0}^{\infty} t^{\alpha-1} e^{-t} d t \\
& \left.=\int_{0}^{\infty} t^{\alpha-1} \left\{\, \frac{d}{d t}-e^{-t}\right.\right\} d t \\
& =\left[-t^{\alpha-1} e^{-t}\right]_{0}^{\infty}+(\alpha-1) \int_{0}^{\infty} t^{\alpha-2} e^{-t} d t \\
& =(0-0)+(\alpha-1) \Gamma(\alpha-1)
\end{align*}
期待値・分散
期待値・分散は定義からパラメータが元の式とは異なる確率密度関数の積分と定数係数に分けて導出する.
期待値の導出
\begin{align*}
\mathbb{E}(X) & =\int_{0}^{\infty} x f_{X}(x) d x \\
& =\int_{0}^{\infty} x \Gamma(\alpha)^{-1} \beta^{-1}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{x}{\beta}} d x \\
& =\Gamma(\alpha)^{-1} \beta^{-1} \int_{0}^{\infty} \frac{\beta x}{\beta}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{x}{\beta}} d x \\
& =\Gamma(\alpha)^{-1} \beta^{-1} \beta \int_{0}^{\infty} \frac{x}{\beta}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{x}{\beta}} d x \\
& =\Gamma(\alpha)^{-1} \int_{0}^{\infty}\left(\frac{x}{\beta}\right)^{(\alpha+1)-1} e^{-\frac{x}{\beta}} d x \\
& =\Gamma(\alpha)^{-1} \Gamma(\alpha+1) \beta \int_{0}^{\infty} \Gamma(\alpha+1)^{-1} \beta^{-1}\left(\frac{x}{\beta}\right)^{(\alpha+1)-1} e^{-\frac{x}{\beta}} d x \\
& =\Gamma(\alpha)^{-1} \alpha \Gamma(\alpha) \beta \\
& =\alpha \beta
\end{align*}
分散の導出
\begin{align*}
\mathbb{E}\left(X^{2}\right)
& = \int_{0}^{\infty} x^{2} f_{X}(x) d x \\
& = \int_{0}^{\infty} x^{2} \Gamma(\alpha)^{-1} \beta^{-1}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{x}{\beta}} d x \\
& = \Gamma(\alpha)^{-1} \beta^{-1} \int_{0}^{\infty} \beta^{2}\left(\frac{x}{\beta}\right)^{2}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{x}{\beta}} d x \\
& = \Gamma(\alpha)^{-1} \beta^{-1} \beta^{2} \int_{0}^{\infty}\left(\frac{x}{\beta}\right)^{(\alpha+2)-1} e^{-\frac{x}{\beta}} d x \\
& = \Gamma(\alpha)^{-1} \beta \Gamma(\alpha+2) \beta \int_{0}^{\infty} \Gamma(\alpha+2)^{-1} \beta^{-1}\left(\frac{x}{\beta}\right)^{(\alpha+2)-1} e^{-\frac{x}{\beta}} d x \\
& = \Gamma(\alpha)^{-1} \beta^{2}(\alpha+1) \alpha \Gamma(\alpha) \\
& = \alpha \beta^{2}(\alpha+1) \\
\end{align*}
よって分散は,
\begin{align*}
V(x)
& =\mathbb{E}\left(x^{2}\right)-\mathbb{E}(x)^{2} \\
& =\alpha \beta^{2}(\alpha+1)-\alpha^{2} \beta^{2} \\
& =\alpha \beta^{2}
\end{align*}
積率母関数
積率母関数の導出
\begin{align*}
M_{x}(t) & =\mathbb{E}\left(e^{t X}\right) \\
& = \int_{0}^{\infty} e^{t x} f_{X}(x) d x \\
& = \int_{0}^{\infty} e^{t x} \Gamma(\alpha)^{-1} \beta^{-1}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{x}{\beta}} d x \\
& = \Gamma(\alpha)^{-1} \beta^{-1} \int_{0}^{\infty}\left(\frac{x}{\beta}\right)^{\alpha-1} e^{-\frac{1}{\beta} x} e^{t x} d x \\
& = \Gamma(\alpha)^{-1} \beta^{-1} \int_{0}^{\infty}\left(x \frac{1}{\beta} \frac{\frac{1}{\beta}-t}{\frac{1}{\beta}-t} \cdot \frac{\beta}{\beta}\right)^{\alpha-1} \exp \left\{-x\left(\frac{1}{\beta}-t\right)\right\} d x \\
& = \Gamma(\alpha)^{-1} \beta^{-1} \int_{0}^{\infty}\left\{x\left(\frac{1}{\beta}-t\right) \cdot\left(\frac{1}{\beta}-t\right)^{-1} \beta^{-1}\right\}^{\alpha-1} \exp \left\{-x\left(\frac{1}{\beta}-t\right)\right\} d x \\
& = \Gamma(\alpha)^{-1} \beta^{-1} \beta^{1-\alpha}\left(\frac{1}{\beta}-t\right)^{1-\alpha} \int_{0}^{\infty}\left\{x\left(\frac{1}{\beta}-t\right)\right\}^{\alpha-1} \exp \left\{-x\left(\frac{1}{\beta}-t\right)\right\} d x \\
& \left.\left.=\Gamma(\alpha)^{-1} \beta^{-\alpha}\left(\frac{1}{\beta}-t\right)^{1-\alpha}\left(\frac{1}{\beta}-t\right)^{-1} \Gamma(\alpha) \int_{0}^{\infty}\left(\frac{1}{\beta}-t\right) \Gamma(\alpha)^{-1} \right\{\, x\left(\frac{1}{\beta}-t\right)\right\}^{\alpha-1} \exp \left\{-x\left(\frac{1}{\beta}-t\right)\right\} d x \\
& = \beta^{-\alpha}\left(\frac{1}{\beta}-t\right)^{-\alpha} \\
& = \left\{\beta\left(\frac{1}{\beta}-t\right)\right\}^{-\alpha} \\
& =(1-t \beta)^{-\alpha}
\end{align*}
積率母関数を用いた期待値の導出
\begin{align*}
\mathbb{E}(X)
&=
M_X(t)' \; |_{t=0}
\\
&=
\frac{d}{dt}(1-t\beta)^{-\alpha} \; |_{t=0}
\\
&=
-\alpha (1-t\beta)^{-(\alpha+1)} \{(1-t\beta)\}' \; |_{t=0}
\\
&=
-\alpha (1-t\beta)^{-(\alpha+1)} (-\beta) \; |_{t=0}
\\
&=
\alpha\beta (1-t\beta)^{-(\alpha+1)} \; |_{t=0}
\\
&=
\alpha\beta (1-0\cdot\beta)^{-(\alpha+1)}
\\
&=
\alpha\beta
\end{align*}
積率母関数を用いた分散の導出
\begin{align*}
\mathbb{E}(X)
&=
M_X(t)'' \; |_{t=0}
\\
&=
\{
\alpha\beta (1-t\beta)^{-(\alpha+1)}
\}'
\; |_{t=0}
\\
&=
\alpha\beta(\alpha+1) (1-t\beta)^{-(\alpha+2)}
\{
(1-t\beta)
\}'
\; |_{t=0}
\\
&=
-\alpha\beta(\alpha+1) (1-t\beta)^{-(\alpha+2)}
(-\beta)
\; |_{t=0}
\\
&=
-\alpha\beta(\alpha+1) (1-t\beta)^{-(\alpha+2)}
(-\beta)
\; |_{t=0}
\\
&=
-\alpha\beta(\alpha+1) (1-0\cdot \beta)^{-(\alpha+2)}
(-\beta)
\\
&=
\alpha\beta^2(\alpha+1)
\end{align*}
\begin{align*}
\mathbb{V}(X)
&=
\mathbb{E}(X^2)-\mathbb{E}(X)^2
\\
&=
\alpha \beta^2(\alpha+1) - (\alpha \beta)^2
\\
&=
\alpha\beta^2
\end{align*}
再生性
ガンマ分布は,パラメータ \alpha について再生性が成立する.
\begin{align*}
\left\{X_{i}\right\}_{i=\{1,2, \ldots, n\}}, \text { i.i.d. } \sim \operatorname{Gam}\left(\alpha_i, \beta \right)
\end{align*}
\begin{align*}
& M_{\sum X_{i}}(t)=\mathbb{E}\left(e^{t \sum X_{i}}\right) \\
& = \mathbb{E}\left(\prod e^{t X_{i}}\right) \\
& =\prod \mathbb{E}\left(e^{t X_{i}}\right) \; \because X_{i} \text {s are i.i.d. } \\
& =\prod \left(1-t \beta \right)^{-\alpha_{i}} \\
& =(1-t \beta)^{-\sum \alpha_{i}} \\
\end{align*}
以上より,
\sum X_{i} \sim \operatorname{Gamma}\left(\sum \alpha_{i}, \beta\right)
ただし,パラメータ \beta について再生性が成立しないので注意.
\begin{align*}
\left\{X_{i}\right\}_{i=\{1,2, \ldots, n\}}, \text { i.i.d. } \sim \operatorname{Gam}\left(\alpha, \beta_{i}\right)
\end{align*}
\begin{align*}
M_{\sum X_{i}}(t)
& =\mathbb{E}\left(e^{t \sum X_{i}}\right) \\
& = \mathbb{E}\left(\prod e^{t X_{i}}\right) \\
& = \prod \mathbb{E}\left(e^{t X_{i}}\right) \; \because x_{i} \text { s are i.i.d. } \\
& = \prod\left(1-t \beta_{i}\right)^{-\alpha} \\
& \neq\left(1-t \sum \beta_{i}\right)^{-\alpha}
\end{align*}
ガンマ分布を用いたベイズモデル (Poasson-Gamma Model)
以下の問題設定を考える.
\begin{align*}
& x \mid \lambda \sim \operatorname{Po}(\lambda), \quad f_{x \mid \lambda}(x)=(x!)^{-1} \lambda^{x} e^{-\lambda} \\
& \lambda \sim \operatorname{Gam}(\alpha, \beta), f_{\lambda}(\lambda)=\Gamma(\alpha)^{-1} \beta^{-1}\left(\frac{\lambda}{\beta}\right)^{\alpha-1} e^{-\frac{\lambda}{\beta}} \\
& \lambda \mid X \sim F_{\lambda | X}(\lambda)
\end{align*}
事後分布の導出
\begin{align*}
\log f_{\lambda|\mathbf{X}}
& = \log f_{\mathbf{X} | \lambda}(\mathbf{X}) f_\lambda(\lambda) \\
& =\log f_{X \mid \lambda}+\log f_{\lambda}(\lambda) \\
& =\log \prod_{i=1}^{N} f_{x}\left(x_{i}\right)+\log f_{\lambda}(\lambda) \\
& \propto \sum\left\{-\log \left(x_{i}!\right)+x_{i} \log \lambda-\lambda\right\}+(\alpha-1) \log \frac{\lambda}{\beta}-\frac{\lambda}{\beta} \\
& \propto\left\{\sum x_{i}\right\} \log \lambda-N \lambda+(\alpha-1) \log \lambda-\frac{1}{\beta} \lambda \\
& =\left\{\alpha+\left(\sum x_{i}\right)-1\right\} \log \lambda-\frac{N \beta+1}{\beta} \lambda
\end{align*}
以上より,事後分布がいかに定まる.
\lambda \mid X \sim \operatorname{Gam}\left(\alpha+\sum x_{i}, \quad \beta(N \beta+1)^{-1}\right)
予測分布の導出
データ \mathbf{X} を観測した後の xの分布を考える.
X_{*} \mid X, \alpha^{\prime} \beta^{\prime} \sim F \\
このとき確率密度関数は,
\begin{align*}
f_{X_{k}}\left(x_{*}\right)
& = \int_{0}^{\infty} f_{X \mid \lambda}(x) f_{\lambda}(\lambda) d \lambda \\
& = \int_{0}^{\infty}(x!)^{-1} \lambda^{x} e^{-\lambda} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime-1}\left(\frac{\lambda}{\beta^{\prime}}\right)^{\alpha-1} e^{-\frac{\lambda}{\beta}} d \lambda \\
& = (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime-1} \int_{0}^{\infty} \lambda^{x} e^{-\lambda}\left(\frac{\lambda}{\beta^{\prime}}\right)^{\alpha-1} e^{-\frac{\lambda}{\beta}} d \lambda \\
& = (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime-1} \int_{0}^{\infty} \exp \left\{-\lambda \left(1+\frac{1}{\beta^{\prime}}\right) \right\} \beta^{\prime x}\left(\frac{\lambda}{\beta^{\prime}}\right)^{x}\left(\frac{\lambda}{\beta^{\prime}}\right)^{\alpha-1} d \lambda \\
& = (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime x-1} \int_{0}^{\infty} \exp \left\{-\lambda\left(1+\frac{1}{\beta^{\prime}}\right)\right\}\left(\lambda \frac{1}{\beta^{\prime}}\right)^{\alpha+x-1} d \lambda \\
= & (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime x-1} \int_{0}^{\infty} \exp \left\{-\lambda\left(1+\frac{1}{\beta^{\prime}}\right)\right\}\left(\lambda \frac{1}{\beta^{\prime}} \frac{1+\frac{1}{\beta^{\prime}}}{1+\frac{1}{\beta^{\prime}}} \cdot \frac{\beta^{\prime}}{\beta^{\prime}}\right)^{\alpha+x-1} d \lambda \\
= & \left.(x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime x-1} \int_{0}^{\infty} \exp \left\{-\lambda\left(1+\frac{1}{\beta^{\prime}}\right)\right\} \lambda\left(1+\frac{1}{\beta^{\prime}}\right)\left(\beta^{\prime}+1\right)^{-1}\right\}^{\alpha+x-1} d \lambda \\
= & (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime x-1}\left(\beta^{\prime}+1\right)^{1-\alpha-x} \int_{0}^{\infty} \exp \left\{-\lambda\left(1+\frac{1}{\beta}\right)\right\}\left\{\lambda\left(1+\frac{1}{\beta^{\prime}}\right)\right\}^{\alpha+x-1} d \lambda \\
= & (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \beta^{\prime x-1}\left(\beta^{\prime}+1\right)^{1-\alpha-x} \Gamma\left(\alpha^{\prime}+x\right)\left(1+\frac{1}{\beta^{\prime}}\right)^{-1} \\
& \left.\left.\int_{0}^{\infty} \Gamma\left(\alpha^{\prime}+x\right)^{-1}\left(1+\frac{1}{\beta^{\prime}}\right) \exp \left\{-\lambda\left(1+\frac{1}{\beta^{\prime}}\right)\right\} \right\{\, \lambda\left(1+\frac{1}{\beta^{\prime}}\right)\right\}^{\alpha+x-1} d \lambda \\
= & (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \Gamma\left(\alpha^{\prime}+x\right) \beta^{\prime} x-1\left(\beta^{\prime}+1\right)^{1-\alpha-x}\left(\frac{\beta^{\prime}}{\beta^{\prime}+1}\right) \\
= & (x!)^{-1} \Gamma\left(\alpha^{\prime}\right)^{-1} \Gamma\left(\alpha^{\prime}+x\right) \beta^{\prime}\left(\beta^{\prime}+1\right)^{-(\alpha+x)}
\end{align*}
この分布をPoisson-Gamma分布という.負の二項分布に対応していることに注意する.最後にこの分布の期待値と分散を求める.
\begin{align*}
\mathbb{E}\left(X_{*}\right) & =\mathbb{E}_{\lambda}\left[\mathbb{E}_{X_{*} \mid \lambda}\left(X_{*} \mid \lambda\right)\right] \\
& =\mathbb{E}_{\lambda}[\lambda] \\
& =\alpha \beta \\
\mathbb{E}\left(X_{*}{ }^{2}\right) & =\mathbb{E}_{\lambda}\left[\mathbb{E}_{X_{*} \mid \lambda}\left(X_{*}{ }^{2} \mid \lambda\right)\right] \\
& =\mathbb{E}_{\lambda}\left[\lambda^{2}+\lambda\right] \\
& =\mathbb{E}_{x}\left[\lambda^{2}\right]+\mathbb{E}_{\lambda}[\lambda] \\
& =\alpha \beta^{2}(1+\alpha)+\alpha \beta \\
V\left(X_{*}{ }^{2}\right) & =\alpha \beta^{2}(1+\alpha)+\alpha \beta-\alpha^{2} \beta^{2} \\
& =\alpha \beta^{2}+\alpha \beta \\
& =\alpha \beta^{2}(1+\beta)
\end{align*}
参考文献
(1) 竹村彰通.”新装改訂版 現代数理統計学”.2020.学術図書出版社
(2) 久保川."現代数理統計学の基礎".2017.共立出版
(3) C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版
(4) 須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.講談社サイエンティフィク
更新
2024.08.14: 構成を一部変更,再生性,ベイズモデルの章を追加



Discussion