[統計学] ベータ分布の期待値と分散

ベルヌーイ分布や二項分布のベイズ推定の記事で, ベータ分布を扱ったので, ベータ分布についても記載します.

確率密度分布

$$\begin{align*} &f(x|a,b) = B(a,b)^{-1}x^{a-1}(1-x)^{b-1}\cdots(1) \\ &\text{Where,} \; B(a,b) = \int_0^1 t^{a-1}(1-t)^{b-1}\;dt \end{align*}$$

期待値・分散

ベータ関数の性質

期待値を求めるにはベータ分布の性質を使うと効率が良い. ベータ関数は以下の性質を持つ.

$$B(a+1,b)=\frac{a}{a+b} B(a,b)\cdots (2)$$

以下証明.

まず, 以下のよう計算を行う.

$$\begin{align*} B(a,b+1) &= \int_0^1 t^{a-1}(1-t)^{b}\;dt \\ &= \int_0^1 \{\frac{1}{a}t^{a}\}'(1-t)^{b-1}\;dt \\ &= [\frac{1}{a}t^{a}(1-t)^{b}]_0^1 - \int_0^1 \frac{1}{a}t^{a}\{(1-t)^{b}\}'\;dt \\ &= [\frac{1}{a}t^{a}(1-t)^{b-1}]_0^1 - \int_0^1 -\frac{b}{a}t^{a}(1-t)^{b-1}\;dt \\ &= (0-0) + \int_0^1 \frac{b}{a}t^{a}(1-t)^{b-1}\;dt \\ &= \frac{b}{a} \int_0^1 t^{a}(1-t)^{b-1}\;dt \\ &= \frac{b}{a} B(a+1,b)\cdots (3) \end{align*}$$

これを用いれば, (2)式左辺を以下のように変形することができる.

$$\begin{align*} B(a+1,b) &= \frac{a}{b}B(a,b+1) \\ &= \frac{a}{b} \int_0^1 t^{a-1}(1-t)^b dt \\ &= \frac{a}{b} \int_0^1 t^{a-1}(1-t)^{b-1}(1-t) dt \\ &= \frac{a}{b} \biggl( \int_0^1 t^{a-1}(1-t)^{b-1} dt - \int_0^1 t^{a}(1-t)^{b-1} dt \biggr) \\ &= \frac{a}{b} \biggl( B(a,b) - B(a+1,b) \biggr)\cdots (4) \end{align*}$$

導出した(4)式を整理する.

$$\begin{align*} B(a+1,b) &= \frac{a}{b} \biggl( B(a,b) - B(a+1,b) \biggr) \\ \frac{b+a}{b} B(a+1,b) &= \frac{a}{b} B(a,b) \\ B(a+1,b) &= \frac{ab}{b(b+a)} B(a,b) \\ &= \frac{a}{(a+b)} B(a,b)\end{align*}$$

期待値

(2)式を用いて, 期待値を導出する.

$$\begin{align*} \mathbb{E}(X) &= \int_0^1 x \frac{1}{B(a,b)} x^{a-1}(1-x)^{b-1}\;dx \\ &= \frac{1}{B(a,b)} \int_0^1 x^{a}(1-x)^{b-1}\;dx \\ &= \frac{1}{B(a,b)}B(a+1,b) \int_0^1 \frac{1}{B(a+1,b)} x^{a}(1-x)^{b-1}\;dx \\ &= \frac{1}{B(a,b)} \frac{a}{(a+b)}B(a,b) \cdot 1 \\ &= \frac{a}{(a+b)} \end{align*}$$

分散

期待値と同様に(2)式を用いて二次のモーメントを求める.

$$\begin{align*} \mathbb{E}(X^2) &= \int_0^1 x^2 \frac{1}{B(a,b)} x^{a-1}(1-x)^{b-1}\;dx \\ &= \frac{1}{B(a,b)} \int_0^1 x^{a+1}(1-x)^{b-1}\;dx \\ &= \frac{1}{B(a,b)}B(a+2,b) \int_0^1 \frac{1}{B(a+2,b)} x^{a+2}(1-x)^{b-1}\;dx \\ &= \frac{1}{B(a,b)} \frac{a+1}{(a+b+1)}B(a+1,b) \cdot 1 \\ &= \frac{1}{B(a,b)} \frac{a+1}{(a+b+1)} \frac{a}{(a+b)} B(a,b) \\ &= \frac{a+1}{(a+b+1)} \frac{a}{(a+b)} \end{align*}$$

以上より,

$$\begin{align*} \mathbb{V}(X) &= \mathbb{E}(X^2)-\mathbb{E}(X)^2 \\ &= \frac{a+1}{(a+b+1)} \frac{a}{(a+b)} - \frac{a^2}{(a+b)^2} \\ &= \frac{a(a+1)(a+b)-a^2(a+b+1)}{(a+b+1)(a+b)^2} \\ &= \frac{a^2(a+b)+a(a+b)-a^2(a+b)-a^2}{(a+b+1)(a+b)^2} \\ &= \frac{a(a+b)-a^2}{(a+b+1)(a+b)^2} \\ &= \frac{ab}{(a+b+1)(a+b)^2} \end{align*}$$

可視化

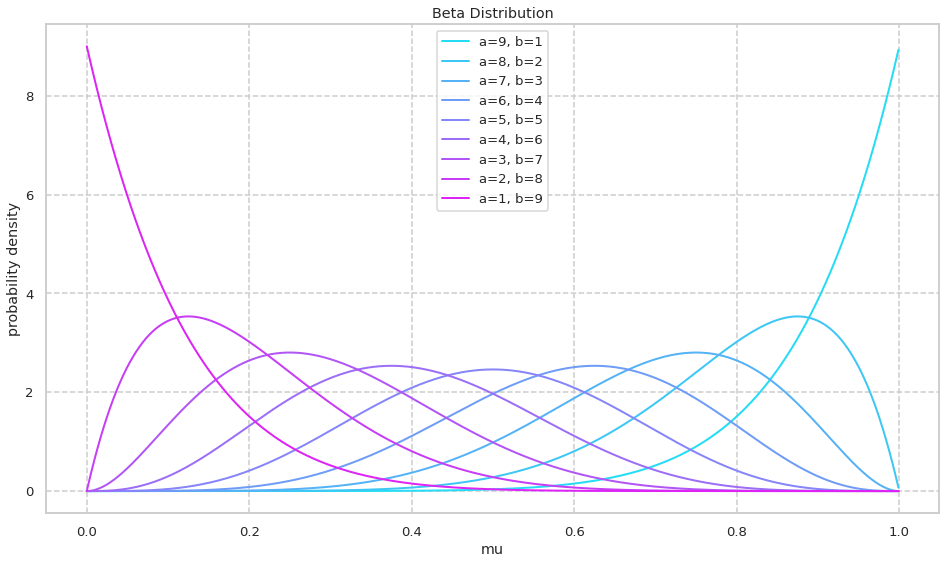
ベータ分布の確率密度関数を確認する. 初めに $a+b=10$ に固定しながら $a,b$ の値を変化させる.

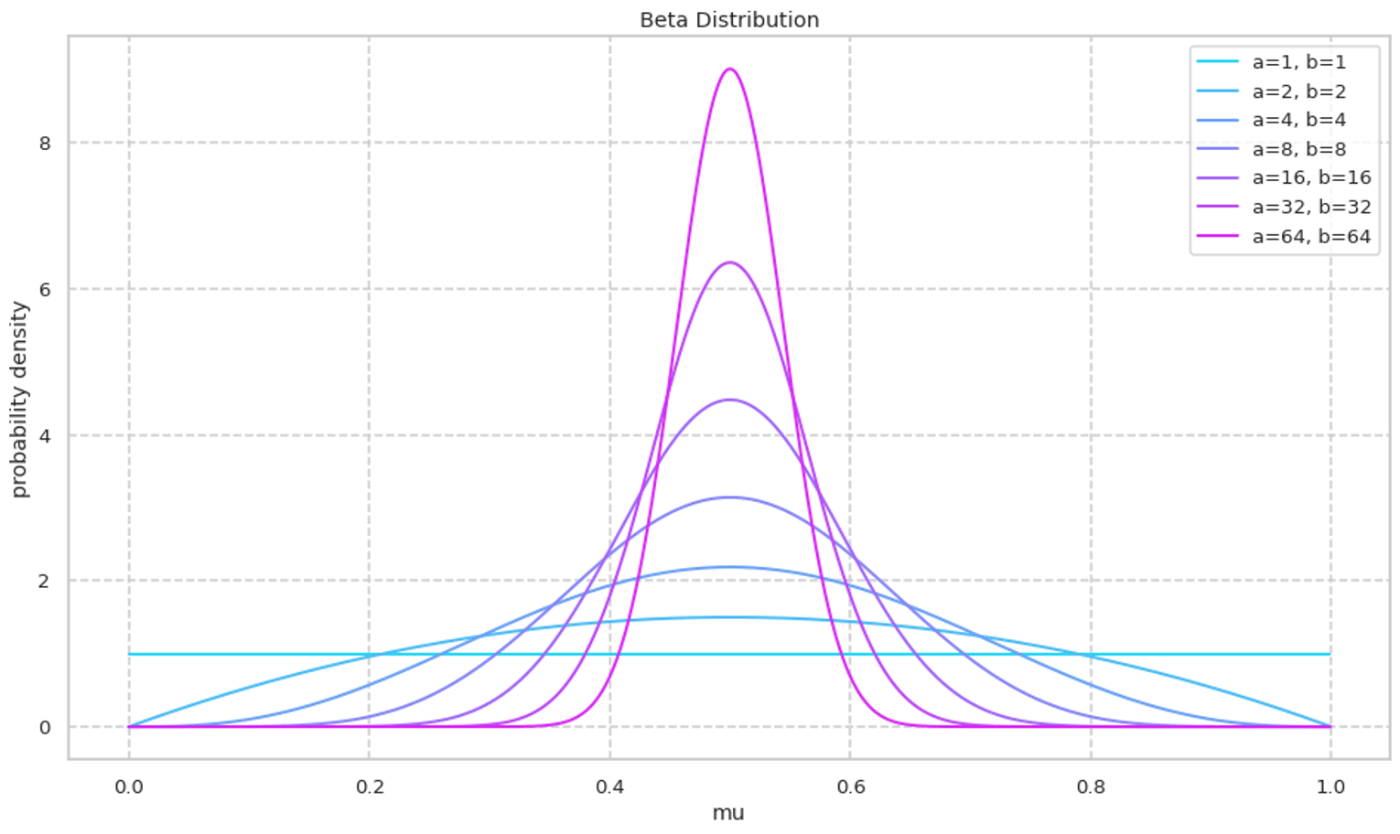
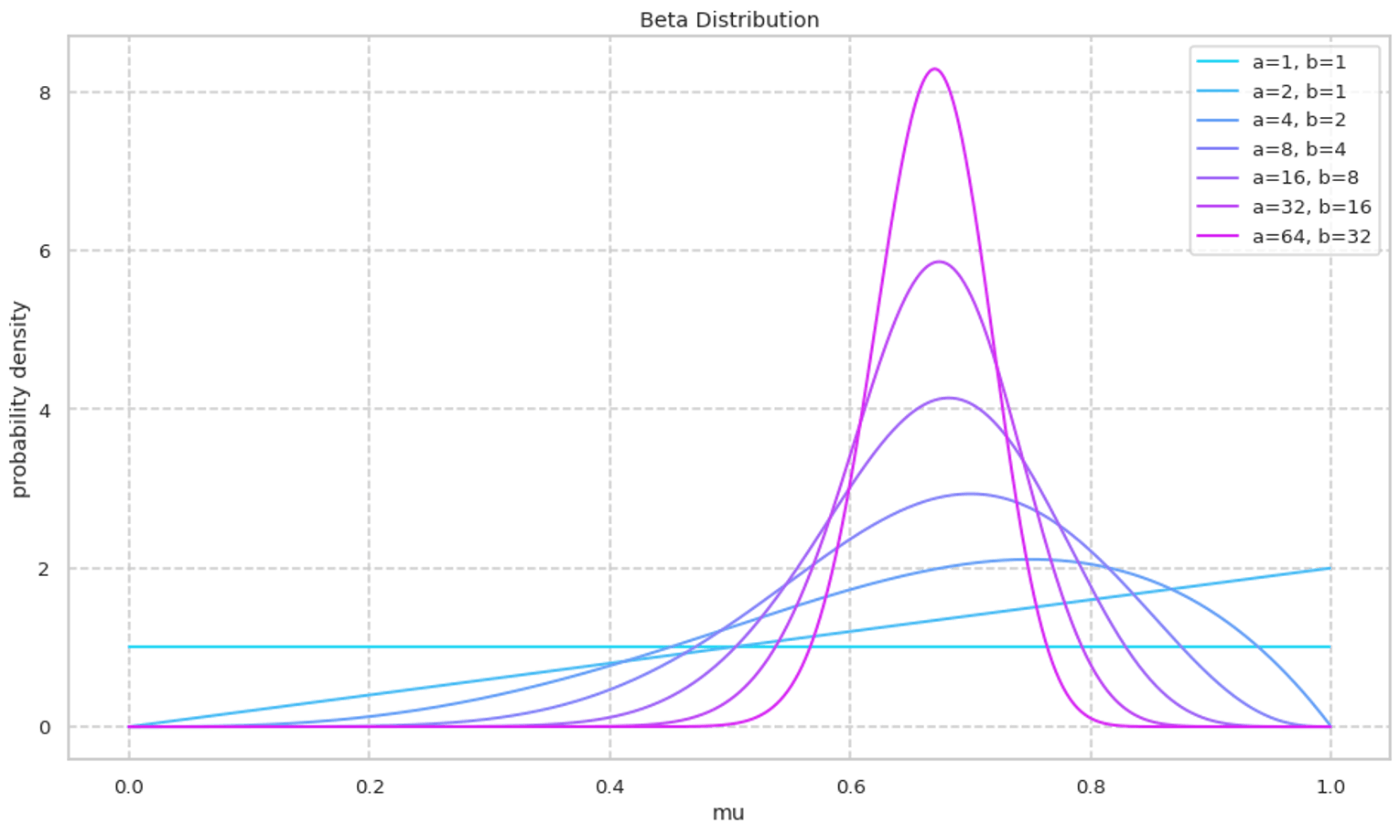
次に a/b を固定しながら $a,b$ の絶対値を大きくしていく様子を可視化する. $a,b$ の絶対値が大きくなるにつれて峰の確率密度が大きくなる様子が確認できる.

Code

3枚あるが, 差分は変数 a_b と ax.legend([...]) のみなので1枚目のみを掲載する.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import beta

a_b = [
    [9,1],
    [8,2],
    [7,3],
    [6,4],
    [5,5],
    [4,6],
    [3,7],
    [2,8],
    [1,9],
]

# data
x = np.arange(0, 1, 0.001)
ys = []
for ab in a_b:
    y = [beta.pdf(x_i, ab[0], ab[1])for x_i in x]
    ys.append(y)

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 2})
sns.set_palette("cool", 9, 0.9)

fig=plt.figure(figsize=(16,9))
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Beta Distribution')
ax1.set_xlabel('mu')
ax1.set_ylabel('probability density')

for ys_i in ys:
    ax1.plot(x,ys_i)

ax1.legend([
    'a=9, b=1',
    'a=8, b=2',
    'a=7, b=3',
    'a=6, b=4',
    'a=5, b=5',
    'a=4, b=6',
    'a=3, b=7',
    'a=2, b=8',
    'a=1, b=9',
])
plt.show()

参考文献

(1) C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版
(2) 須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.講談社サイエンティフィク