期待値を累積分布関数の積分の和に分解
よく忘れる変形なので,メモがてら残す.
期待値は,以下のように分解できる.
\begin{align*}
\mathbb{E}(X)
& = \int x f_{X}(x) d x \\
& = \int_{-\infty}^{0} x f_{X}(x) d x+\int_{0}^{\infty} x f_{X}(x) d x \\
& =
- \int_{-\infty}^{0} \left\{ \int_{x}^{0} d t\right\} f_{X}(x) d x
+ \int_{0}^{\infty}\left\{\int_{0}^{x} d t\right\} f_{X}(x) d x \\
& =
- \int_{-\infty}^{0} \int_{-\infty}^{t} f_{X}(x) d x d t
+ \int_{0}^{\infty} \int_{t}^{\infty} f_{X}(x) d x d t \\
& =
- \int_{-\infty}^{0} F_{X}(t) d t
+ \int_{0}^{\infty}\{1-F_{X}(t)\} d t
\end{align*}
2行目から3行目の式変形で以下の変換を用いていることに注意.
x =
\begin{cases}
\int_{0}^{x} d t \\
-\int_{x}^{0} d t
\end{cases}
\begin{align*}
\int_{0}^{x} d t & =[t]_{0}^{x}=x \\
-\int_{x}^{0} d t & =-[t]_{x}^{0}=x \\
\end{align*}
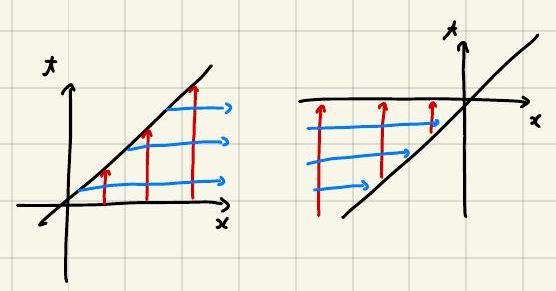
また,3行目から4行目の式変形でxを固定してtを動かす積分から,tを固定してxを動かす積分に変形していることに注意.
出典
久保川."現代数理統計学の基礎".2017.共立出版


Discussion