三角関数sinとcosの基礎
概要
私は文系出身で数学力が四則演算レベルでスタートしたので、
Three.jsを勉強している際にとても苦労しました。(今もしています。)
三角関数はsinやcosのことですが、
高校時代に学習したものの実生活の色々な場面で三角関数の考え方が使われているとは知らずにテストのための勉強をしていました。
今回は、
三角関数についてThree.jsのコードを交えてまとめていこうと思います。
まず、数学としての三角関数
三角関数とは何でしょう?
直角三角形の2辺の長さの比を分数で表現したもの。
つまり、辺の比のことです。
2種類の三角関数の考え方があります。
(Three.jsで三角関数を利用することにおいては1より2が重要かも??)
1. 純粋な直角三角形を基に考える。
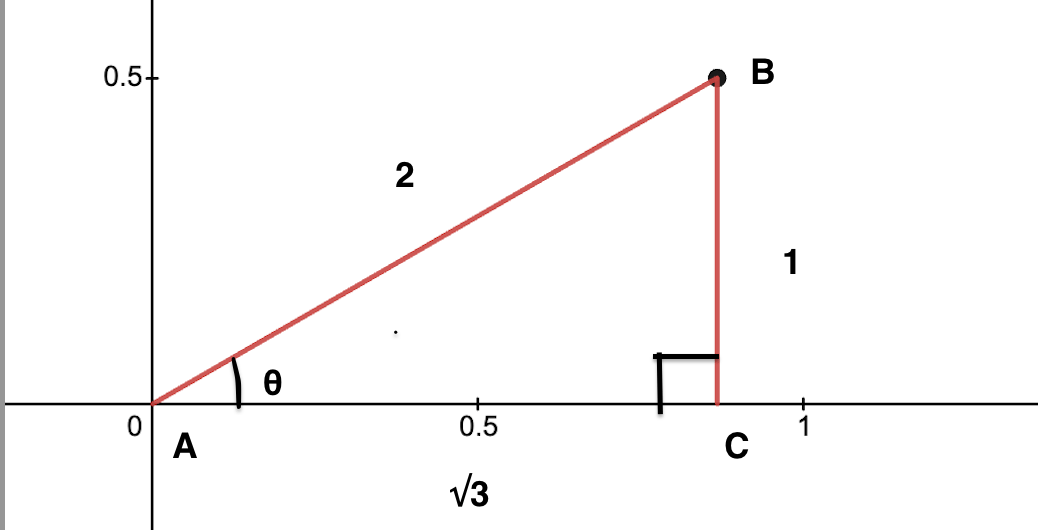
公式
sinθ=BC/AB
cosθ=AC/AB
tanθ=BC/AC
上図の場合
sinθ=1/2
cosθ=√3/2
tanθ=1/√3
覚え方

このような辺の比などを利用して実際の高さなどを計算して求めることができます。
以下のサイトなどで実際に問題を解いてみると理解が深まると思います。
2. 半径1の円(単位円)を基に考える。
単位円
半径1の円。
前提知識
π (180度) = 3.14 半周
2π (360度) = 6.28 1周
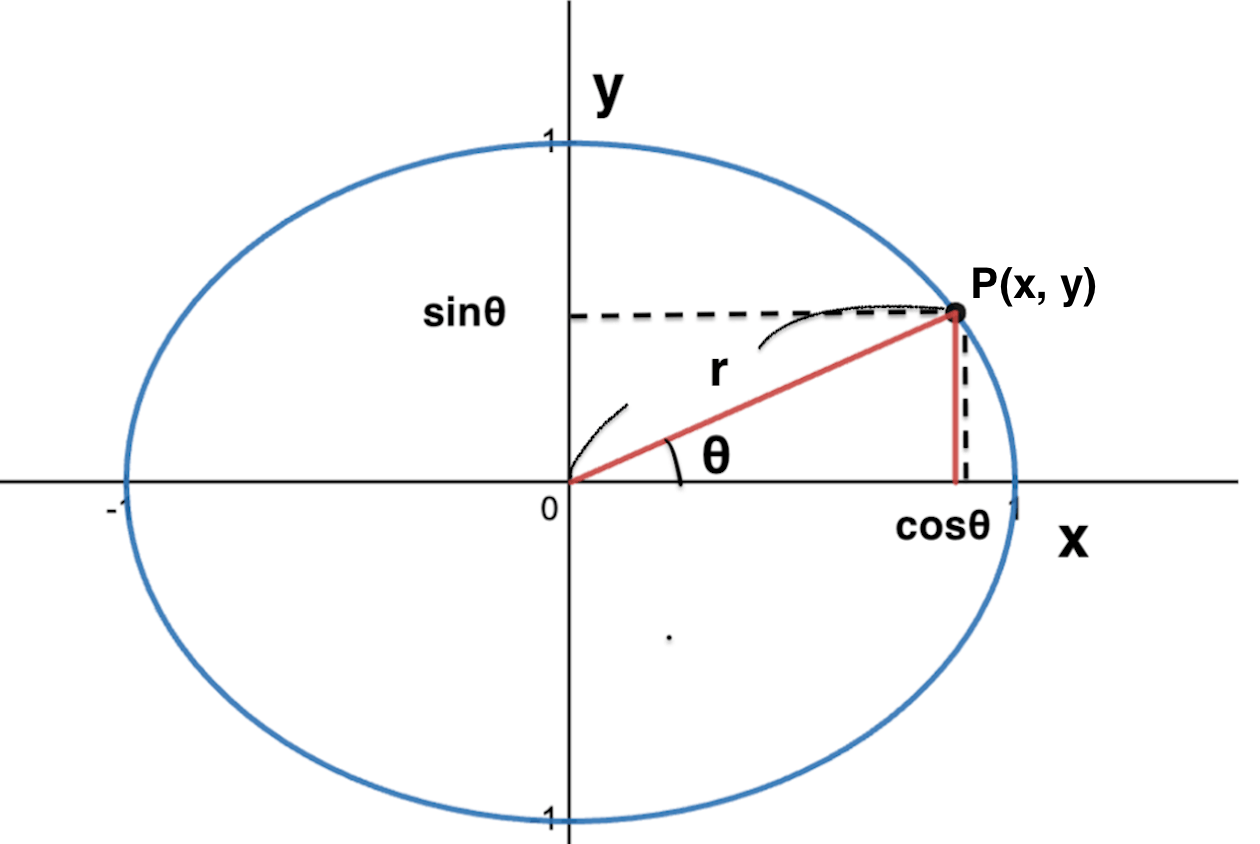
公式
sinθ=y/r
cosθ=x/r
tanθ=y/x
↓単位円なのでrに1を代入します。
sinθ=y
cosθ=x
tanθ=y/x
つまり、二次元座標P(x, y)において、
- cosが横方向の移動量x
- sinが縦方向の移動量y
となります。
sin/cosの活用
sin/cosはクリエイティブコーディングをする上で、避けては通れないものとなっています。
先ほどの2の考え方を利用すると以下の図のような動きを表現することができる。
- 波形状のもの(バネなど)
- 円運動

画像引用
半径1の円を基準にしているため、sin/cosの結果の範囲は必ず-1~1の範囲になります。
GLSL Grapherで動きを確認する
sinの動き
角度が0度の時の長さyは0
角度が90度の時の長さyは1(図で表すと3.14 / 2 = 1.57あたり)

cosの動き
角度が0度の時の長さyは1
角度が90度の時の長さyは0(図で表すと3.14 / 2 = 1.57あたり)
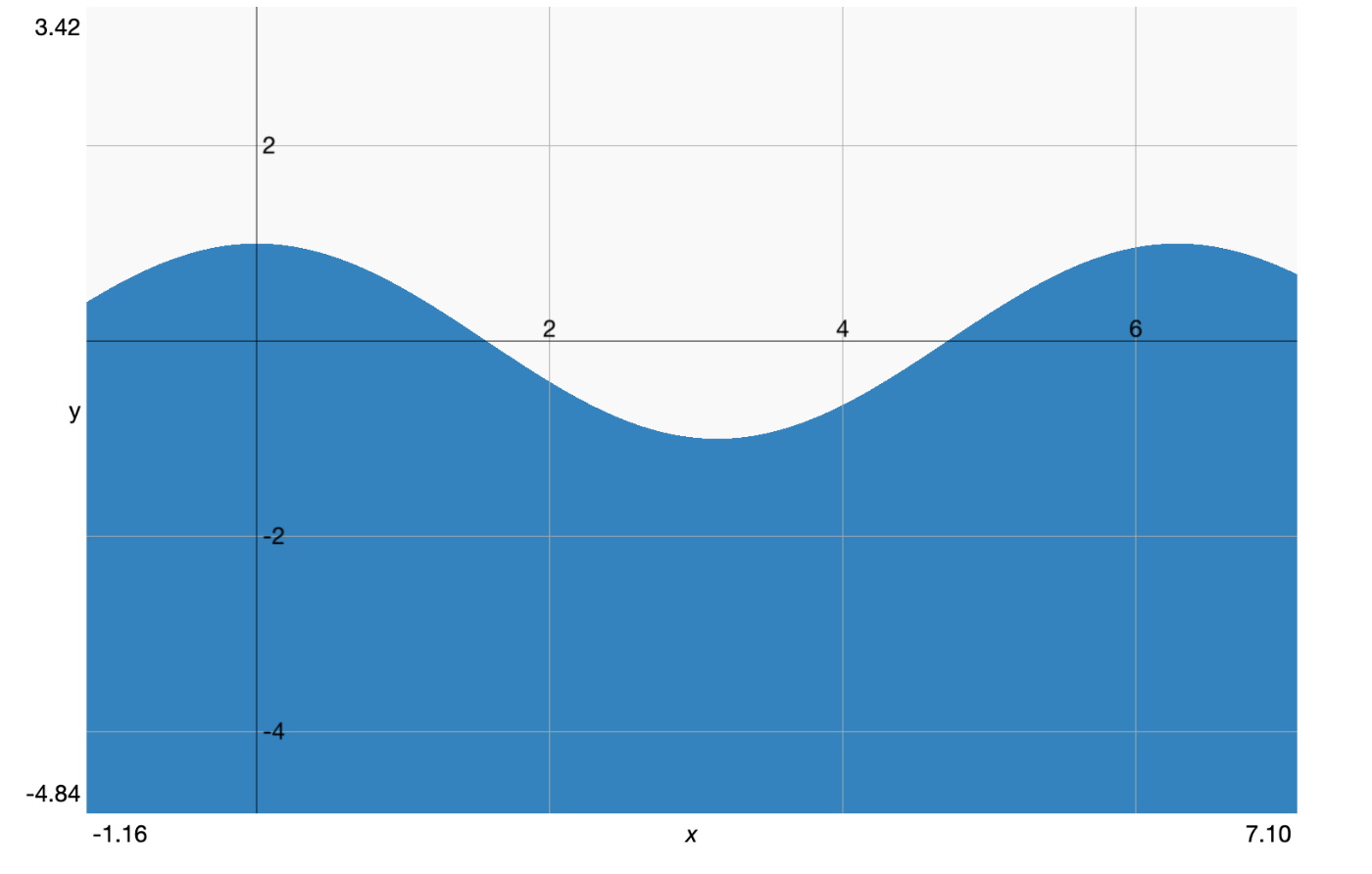
sinもcosも動きとしては変わりません。
sinとcosは90度ずれてるだけです。
コードで確認
今回は簡単な例としてsin/cosを利用して円状にオブジェクトを等間隔に配置します。
sin/cosは一定周期ごとに上下する表現が可能になるので、
以下のコードは
- x軸にMath.cosを使用して一定周期ごとに上下させる。
- y軸にMath.sinを使用して一定周期ごとに上下させる。
結果的に円運動を表現しています。

const MESH_COUNT = 30;
for (let i = 0; i <= MESH_COUNT; i++) {
const angle = 360 / MESH_COUNT;
const angle_rag = (Math.PI / 180) * angle;
const geometry = new THREE.DodecahedronGeometry(0.003 * i, 2);
const material = new THREE.MeshPhongMaterial({
color: 0x0000ff,
wireframe: true,
});
const mesh = new THREE.Mesh(geometry, material);
const x = Math.cos(i * angle_rag);
const y = Math.sin(i * angle_rag);
mesh.position.set(x, y, 0.0);
this.scene.add(mesh);
}
他にもx軸のみ又はy軸のみsinやcosを使用して上下運動させることで波形状のものを表現することができます。
また、z軸にsinやcosを代入すると、手前側と奥側で上下運動を表現することができます。
これらを組み合わせて応用していくと複雑な波のようなもの動きも表現できます。
感想
クリエイティブコーディングにおける三角関数のsin/cosについてまとめました。
まとめたものの、まだ「理解した!」という実感は全くありません。
雰囲気を掴めたという感じです。
クリエイティブコーディングの数学とか物理において、「今は分からないけど、いつか分かるだろう」みたいな割り切りは必要かも知れないです。

Discussion