巡回セールスマン問題を深層学習と強化学習で解く

こんにちは！shu421と言います。

数理最適化 Advent Calendar 2023 の 12 日目です。今回は巡回セールスマン問題 (Traveling Salesman Problem: TSP) を深層学習と強化学習で解く方法を紹介します。最近の動向をざっくり追うだけなので、詳細については各論文を参考にしていただけたらと思います。

目次

• 巡回セールスマン問題とは
• 深層学習と強化学習を使う理由
• 論文紹介
  1. Neural Combinatorial Optimization with Reinforcement Learning
  2. Attention, Learn to Solve Routing Problems!
  3. Solving combinatorial optimization problems over graphs with BERT-Based Deep Reinforcement Learning
• まとめ

巡回セールスマン問題とは

巡回セールスマン問題(Traveling Salesman Problem: TSP)とは、都市の集合と各都市間の距離が与えられたとき、全ての都市を一度だけ訪れて出発地に戻る最短の経路を求める問題です。以下の図のように、都市を頂点、都市間の距離を辺としたグラフで表現することができます。

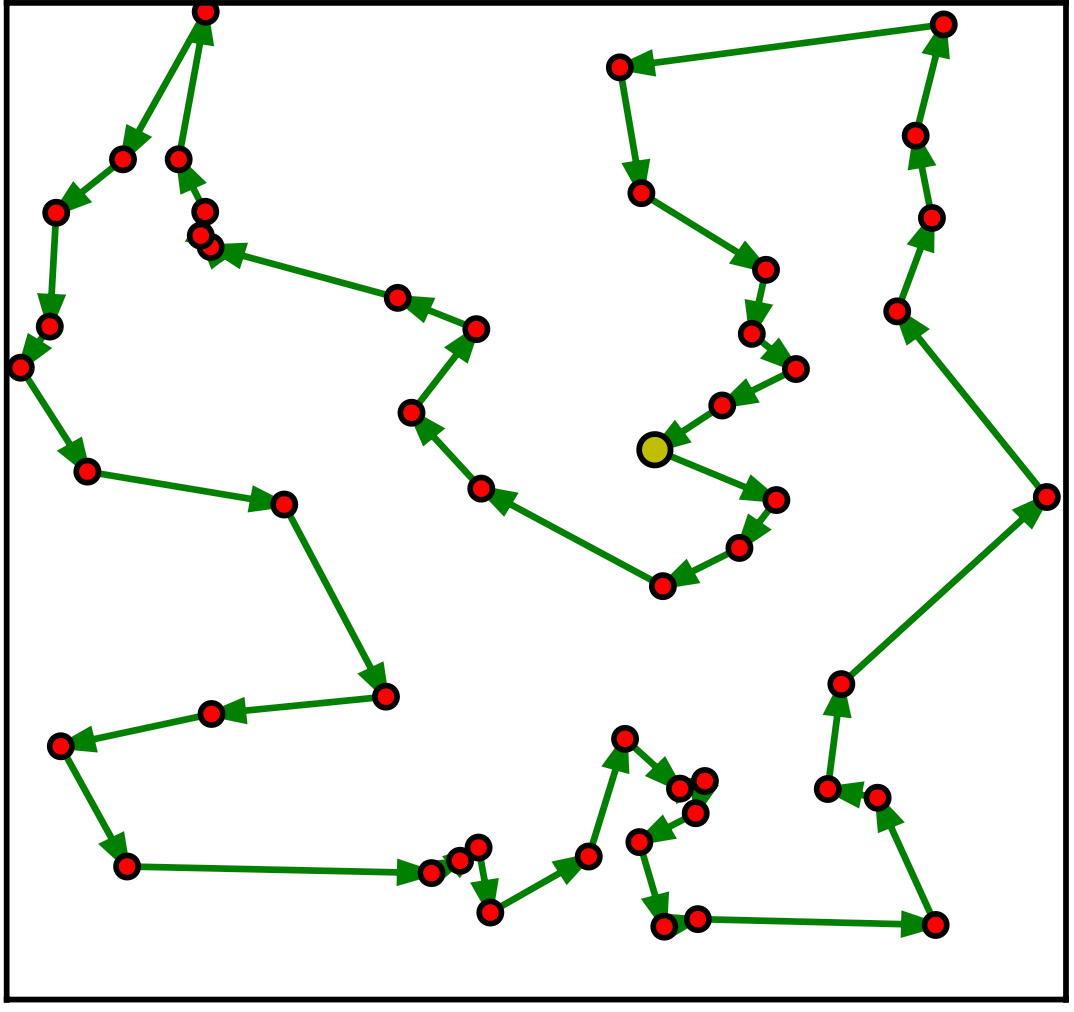
50 都市の TSP の例 [2]

定式化は以下のようになります。

$$\begin{align} & \text{minimize} & \sum_{i=1}^{n} \sum_{j=1}^{n} c_{ij} x_{ij} \\ & \text{subject to} & \sum_{i=1}^{n} x_{ij} = 1 & \quad \forall j \in \{1, \dots, n\} \\ & & \sum_{j=1}^{n} x_{ij} = 1 & \quad \forall i \in \{1, \dots, n\} \\ & & \sum_{i \in S} \sum_{j \in S} x_{ij} \leq |S| - 1 & \quad \forall S \subset \{1, \dots, n\}, 2 \leq |S| \leq n-1 \\ & & x_{ij} \in \{0, 1\} & \quad \forall i, j \in \{1, \dots, n\} \end{align}$$

ここで、$n$ は都市の数、$c_{ij}$ は都市 $i$ から都市 $j$ への距離、$x_{ij}$ は都市 $i$ から都市 $j$ への移動を表すバイナリ変数で、移動がある場合は1、ない場合は0となります。目的関数は総移動距離を表しています。制約条件は以下の通りです。

• 各都市から出る辺は1本 (2)
• 各都市に入る辺は1本 (3)
• 部分巡回路を作らない (4)

部分巡回路を回避するための制約は MTZ 制約と呼ばれます。上記の定式化以外にも他の定式化が提案されています。

TSP は NP 困難問題であるため、大きな問題において厳密解を求めるのは困難です。そのため、問題サイズが大きい場合は、ヒューリスティック解法を用いて近似解を求めます。これから紹介する深層学習と強化学習を使用する手法もヒューリスティック解法の一部です。

深層学習と強化学習を使う理由

さて、TSP に対して深層学習と強化学習を使う理由は何でしょうか。それは、TSP を含む組合せ最適化問題は問題サイズに対して計算量が指数的に増加するという性質を持っているためです。TSP の場合、都市数を $n$ とすると経路の総数は数珠順列として考えられ、 $\frac{n!}{2n} = \frac{(n-1)!}{2}$ (つまり計算量は $O(n!)$) となります。具体的な値を求めてみると、$n=10$ では $181,440$ 通り、$n=30$ では $4.42 \times 10^{30}$ と、天文学的な数字となります。

したがって、TSP では問題サイズが大きくなると厳密解を求めるのは困難になります。一方で、深層学習モデルは問題サイズに対して計算量が多項式的に増加するため、計算量が増えにくく高速に解を求めることができます。

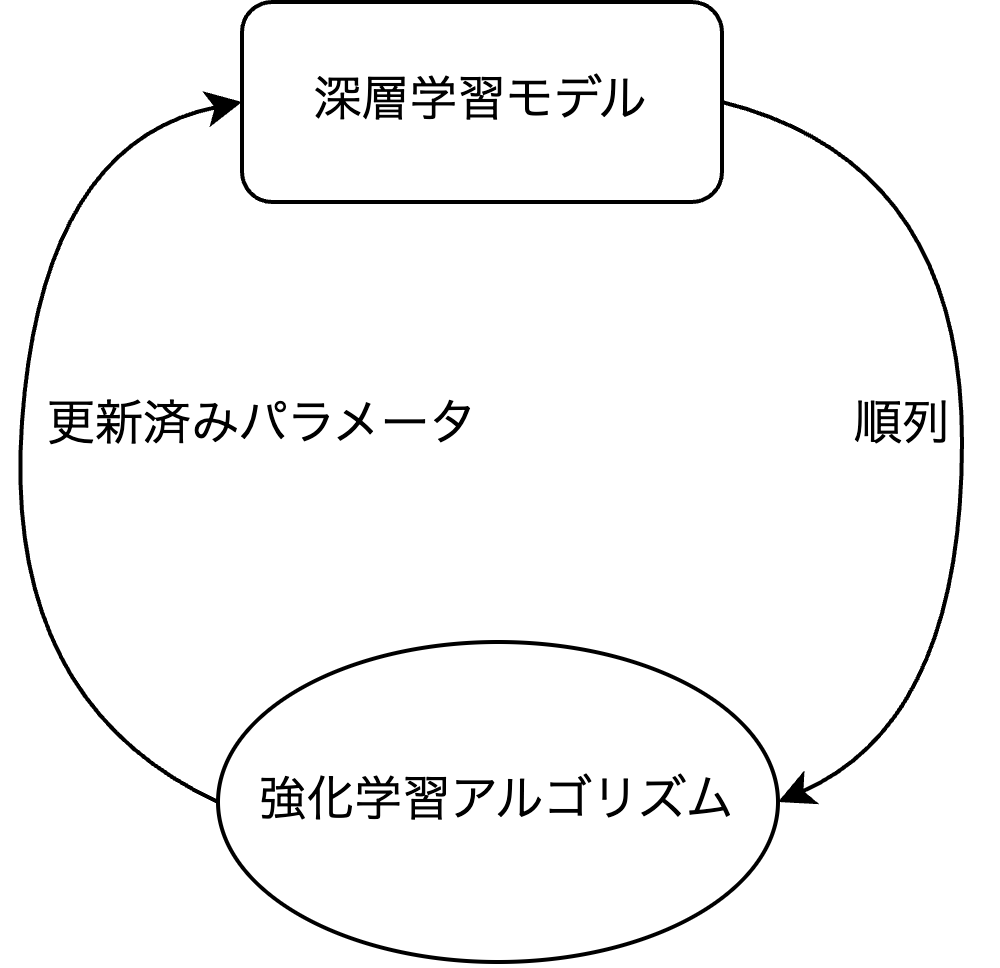
では、深層学習モデルはどのように学習させるのが良いでしょうか。もし教師あり学習を使うのであれば、都市集合と都市を巡る順列のペアを用意する必要があります [1]。この順列は事前にソルバーを使って問題を解いた結果です。しかし、深層学習モデルの精度を出すには多くの学習データを用意する必要がありますが、ソルバーを使って事前に大量の順列を生成するのは現実的ではありません。

そこで、教師あり学習とは異なり正解の順列を必要としない強化学習を使おうという取り組みがあります。強化学習では良い解を自動で探索しながら学習するため、正解の順列を事前に用意する必要がなくソルバーを使わずに深層学習モデルを学習することができます。

論文紹介

深層学習と強化学習を使って TSP を解く手法の中で、個人的に重要だと感じたものを3つピックアップして紹介します。詳細については各論文を読んでいただけたらと思います。

1. Neural Combinatorial Optimization with Reinforcement Learning [2]

Pointer Networks [3] を強化学習により学習し、TSP を解くという手法です。Pointer Networks は入力系列のインデックスに対応する出力系列のインデックスを予測する、LSTM ベースの深層学習モデルです。Pointer Networks は decoding 時にこれまで選択したインデックスを選択しない機構を導入しており、これによって全ての都市にちょうど一度だけ訪れるという TSP の制約条件を満たします。日本語の解説記事ですと、こちらがわかりやすいかなと思います。

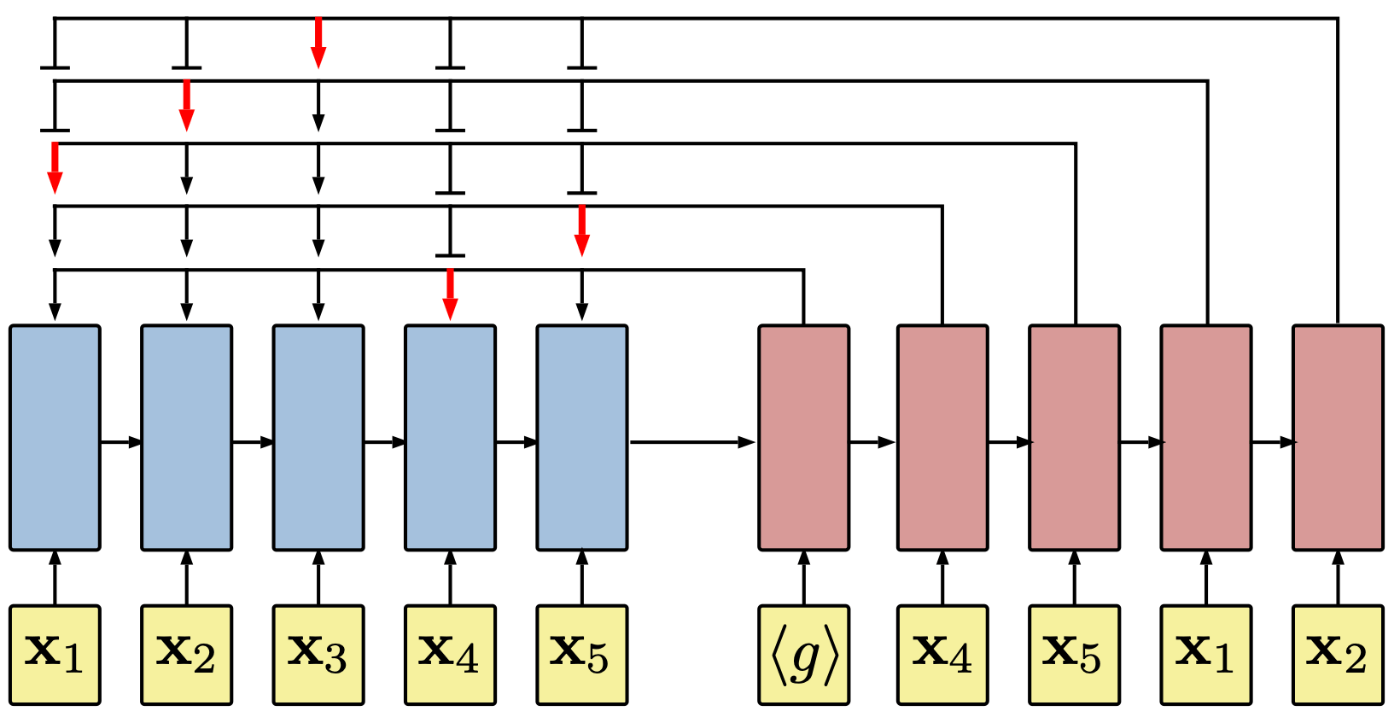
Pointer Networksのアーキテクチャ [3]。<g>(=スタートトークン) から始まる decoding では、これまで選択したインデックスを選択していないことがわかります。

2. Attention, Learn to Solve Routing Problems! [4]

近年、自然言語処理分野では Transformer をベースとしたモデルが高い精度を出しています。この論文では以前まで使用されていた LSTM ベースの Pointer Networks [2] に代わり、Transformer ベースの深層学習モデルである Attention Model (AM) を用いて TSP を解きます。Attention Model に含まれる Multi Head Attention という機構により、LSTM よりも柔軟な表現を得ることができ高い精度を達成しました。

3. Solving combinatorial optimization problems over graphs with BERT-Based Deep Reinforcement Learning [5]

自然言語処理分野で大活躍している BERT をベースとした BDRL という深層学習モデルを用いて TSP を解くという手法です。深層学習モデルのアーキテクチャは Attention Model [3] とほとんど同様ですが、BERT と同じように入力系列の一部をマスクする事前学習し、解きたい問題ごとにファインチューニングすることで、高い精度と汎用性を達成しました。TSP や CVRP など2次元ユークリッド空間を扱う問題であれば、ファインチューニングすることで簡単にタスク特有のネットワークを得ることができます。

比較

都市数が20、50、100の2次元ユークリッド空間上において、ソルバー、ヒューリスティクス、深層学習と強化学習を用いる手法を目的関数値、目的関数値の最適値とのギャップ、求解時間の観点から比較しました。結果は以下の通りです [5]。

手法	TSP20 目的関数値	ギャップ	求解時間	TSP50 目的関数値	ギャップ	求解時間	TSP100 目的関数値	ギャップ	求解時間
Concorde	3.84	0.00 %	1 m	5.70	0.00 %	2 m	7.76	0.00 %	3 m
LKH3	3.84	0.00 %	18 s	5.70	0.00 %	5 m	7.76	0.00 %	21 m
OR Tools	3.85	0.37 %	–	5.80	1.83 %	–	7.99	2.90 %	–
Nearest Insertion	3.84	0.00 %	18 s	6.78	19.03 %	2 s	9.46	21.82 %	6 s
Random Insertion	3.85	0.37 %	–	6.13	7.65 %	1 s	8.52	9.69 %	3 s
Farthest Insertion	3.93	2.36 %	1 s	6.01	5.53 %	2 s	8.35	7.59 %	7 s
PN-AC [2]	3.89	1.42 %	–	5.95	4.46 %	–	8.30	6.90 %	–
AM [4]	3.85	0.34 %	0 s	5.80	1.76 %	2 s	8.12	4.53 %	6 s
BDRL [5]	3.84	0.00 %	0 s	5.73	0.53 %	1 s	7.81	0.64 %	3 s

Concorde は分枝カット法を用いたソルバー、LKH3 は Lin-Kernighan-Helsgaun アルゴリズムを用いたヒューリスティックソルバー、OR Tools は Google の数理最適化ツールです。

Nearest・Random・Farthest Insertion はそれぞれ最も近い都市、ランダム、最も遠い都市を順に挿入していくヒューリスティック解法です。

PN-AC は Pointer Networks を使用する手法 [3] のうち、経路生成時に Active Search という手法を用いたものです。経路生成時にも学習をするため、推論時間が長くなります。

結果を見ると、AM と BDRL では高速に良い近似解を求めていることがわかります。特に BDRL は TSP20 で最適解、TSP100 でも最適解に近い解を求めています。

20231214 追記) こちらの実験結果は BDRL 以外は 10,000 インスタンスでの合計値です [4]。おそらく BDRL に関しても合計値だとは思いますが、論文に明記されていなかったので参考程度にしていただけると幸いです。

まとめ

深層学習と強化学習を使って TSP を解く手法を紹介しました。深層学習と強化学習を使うことで、TSP のような組合せ最適化問題を高速に良い解を求めることができます。また、深層学習モデルはファインチューニングすることで汎用性を持たせることができるため、TSP 以外の組合せ最適化問題にも応用することができます。深層学習や強化学習の研究はまだまだ進んでいるため、今後の発展が楽しみです。

参考文献

[1] Bertsimas, D., & Stellato, B. (2022). Online mixed-integer optimization in milliseconds. INFORMS Journal on Computing, 34(4), 2229-2248.

[2] Bello, I., Pham, H., Le, Q. V., Norouzi, M., & Bengio, S. (2016). Neural combinatorial optimization with reinforcement learning. arXiv preprint arXiv:1611.09940.

[3] Vinyals, O., Fortunato, M., & Jaitly, N. (2015). Pointer networks. Advances in neural information processing systems, 28.

[4] Kool, W., Van Hoof, H., & Welling, M. (2018). Attention, learn to solve routing problems!. arXiv preprint arXiv:1803.08475.

[5] Wang, Q., Lai, K. H., & Tang, C. (2023). Solving combinatorial optimization problems over graphs with BERT-Based Deep Reinforcement Learning. Information Sciences, 619, 930-946.