Zenn
💫

強化学習の基礎的な手法で簡単なRPG風ゲームを攻略してみた

に公開
Python
強化学習
tech

強化学習を勉強したい！

そう思っていろいろな資料を読み漁るなどして、勉強に励んできました。
が、数式や最適化手法をいろいろ追いかけるよりも、実際に使ってみたほうが頭に入りそう。
というわけで、簡単なゲームを設定して強化学習の基礎的な手法を適用してみました。

強化学習について

強化学習の基本的な知識については、他の方々の素晴らしい記事がございますので、そちらを参照いただければと。
以下の動画が非常に分かりやすく、大いに参考にさせていただきました。おすすめです。
https://youtube.com/playlist?list=PLhDAH9aTfnxI1OywfnxXCDTWGtYL2NxJR&si=6-1-2sZPHojnY8mn

ゲームの設定

以下のようなゲームを設定しました。

ルール

  • 初期状態に、health (今回は 12) が与えられ、行動を選択してgoldを最大化することが目的。
  • round(行動回数)は5。
  • 行動によってhealthを消費し、healthが0になった場合は、goldが自動的に0になる。(死亡)
  • 行動は以下の３つから選択でき、効果は以下の通り。
    1. adventure: healthを1,2,3,4,5からランダムで消費し、10倍のgoldを得る。
    2. investment: 体力を3減らして金額を1.5倍にする。
    3. save: healthを1減らす。
あるエピソードの例

Round(1) : State(h=12, g=0) -> Action=adventure
Round(2) : State(h=9, g=30) -> Action=adventure
Round(3) : State(h=6, g=60) -> Action=investment
Round(4) : State(h=3, g=90) -> Action=save
Round(5) : State(h=2, g=90) -> Action=save
Final: h=1, g=90

強化学習の文脈では、プレイ開始から終了までの1回のゲームプレイをエピソードと呼ぶそうです。

期待される戦略

このゲームを攻略するために、おおよそ以下のような戦略が適切だと考えられます。

  • とりあえず最初は adventure がいい。
  • 死にかけ (例：3ターン目行動選択時点で残りhealthが4) の時はひたすらsaveするのが最適。
  • goldが60より大きい時はinvestmentの方が良い行動
    (期待値を考えた場合。最高記録を狙うとかの場合は話が変わってくる。)

Let's 強化学習

さっそく強化学習でこのゲームを解いていきます。

ゲームについて強化学習の文脈で整理する

まず、強化学習で用いられる変数や関数を、このゲームに合わせて整理します。

s : 状態 (state)

ゲームとしてどんな状況にあるか。このゲームの場合は、round数、残りhealth、goldが決まることによって、一意に決まります。

a : 行動 (action)

プレイヤーの行動。このゲームの場合、"adventure","investment","save" のうちどれかを選ぶことです。

r : 報酬 (reward)

ゲームスコアのこと。今回のゲームの場合はゲーム終了後に得られるgoldのことであり、これを最大化するように学習が行われます。

Q_{\text{new}}(s,a), Q(s,a) : 行動価値関数

s,a が決まったら、その行動の価値を示す値を返す関数です。具体的にどのような値になるかは、最適化の方法によって変わります。
強化学習では、実際にゲームをプレイしてみて、その結果をこの行動価値関数に反映していくことによって、報酬を最大化する行動が何か探索していきます。

最適化手法について

価値関数の最適化手法は、モンテカルロ法、Q学習を使用しました。

モンテカルロ法
Q(s, a) \;\leftarrow\; Q(s, a) \;+\; \alpha \,\bigl[G_t - Q(s, a)\bigr]
G_t \;=\; \sum_{k=0}^{T-t} \gamma^k \, r_{t+k}

( T:全ラウンド数、t:現在のラウンド数、\gamma:割引率(0\leqq\gamma\leqq1)、\alpha:更新率(0\leqq\alpha\leqq1))

ここで、G_tとは、その後に得られる報酬を全て減衰率をかけたうえで全て足し合わせた値になります。現在のラウンドから遠いラウンドで発生した報酬ほど、減衰率が高くなり、G_tに対する影響が小さくなるという式になっています。今回は、ゲーム終了後のみ報酬が発生しますが、一般的には各行動の後に毎回報酬が発生します。
t=3の場合のを計算した場合のイメージ
更新式については、下の図のように、Q(s,a)をG_tに近づけていく式だと解釈することができます。ただし、このG_tはあくまで1回ゲームをプレイしただけで得た結果であるため、信用し過ぎず\alphaをかけて更新しています。下の絵でいうと、一番左のバーが現在のQ(s,a)で一番右のバーがG_tとなっており、更新式の右辺はこれらの中間の値になります。
更新式のイメージ
コードは以下の通り。episode_state_actionはゲームプレイ1回分の履歴が入っています。final_rewardを確認して、再度for文を回して、通ってきたs(状態)に対して\gammaをかけた報酬をフィードバックしていきます。

for sc in range(step_count+1):
    t_s, h_s, g_s, a_s = episode_states_actions[sc]
    Q[t_s, h_s, g_s, a_s] += alpha * (final_reward*(gamma**(step_count-t_s)) - Q[t_s, h_s, g_s, a_s])
Q学習

以下のような関数で学習します。

Q_{\text{new}}(s,a) \leftarrow Q(s,a) + \alpha \Big[ r + \gamma \max_{a’} Q(s’,a’) - Q(s,a) \Big]

( Q_{\text{new}}(s,a), Q(s,a) : 行動価値関数、 \alpha : 学習率、 \gamma : 割引率、 s’,a’ : それぞれ一つ次のターンの状態と行動)
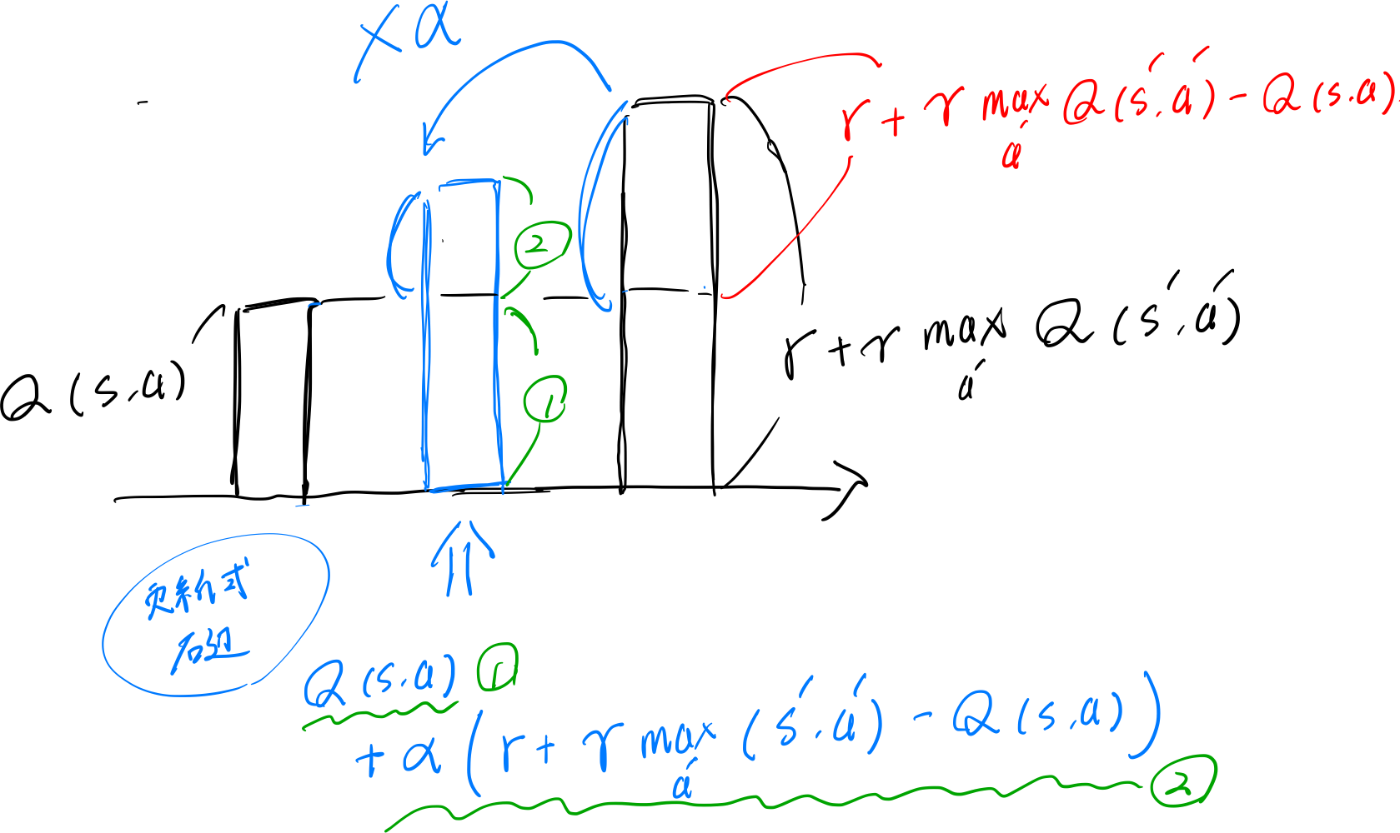
先ほどと同じような解釈で更新式をグラフ化してみると以下のようになります。
Q(s,a)をr + \gamma \max_{a’} Q(s’,a’)に近づける式だと解釈することができます。
Q学習の更新式のイメージ

実装

いくつかパラメータを設定して実験ができるように設計したコードが以下になります。
Colabで開く

EPSILONS・DECAY_RATESについて

コードを見ていただけると分かりますが、最初に"とりあえずプレイしてみる"という処理が入ります。
この際に、一定の確率でランダムな選択を行い、それ以外の場合は現状で最適な行動をとる戦略をとっています。
ランダムな選択を行う確率として、初期値をEPSILON、一回ゲームプレイするごとにDECAY_RATEをかけた値を使います。DECAY_RATEは1未満に設定され、学習が進むごとにランダムな行動の確率を低くしていきます。
最初はランダムな行動を多くして、さまざまなパターンを学習し、だんだん最適な行動がわかってきたら、その行動を多めにする。そんなイメージです。

結果

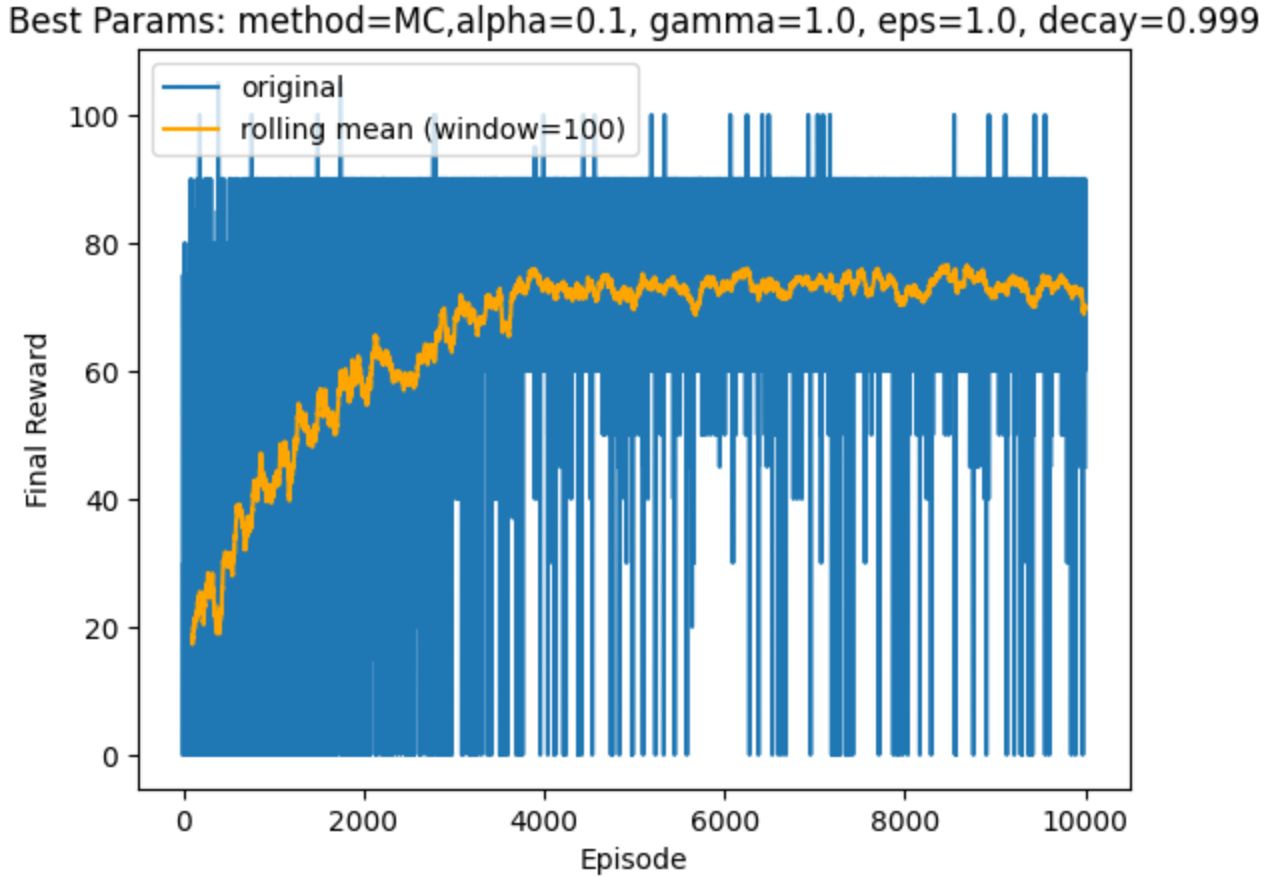
以下に示すグラフは、横軸が Episode (ゲームプレイを試行した回数) で、縦軸が reward (最終的に獲得した報酬)であり、学習が進むにつれて結果が改善していることが分かります。
結果の一例

どのくらい賢いか

最後に、この記事の上の方で考えた「期待される戦略」と実際の行動を照らし合わせて、どのくらい賢くなったか確認してみます。

# ゲームプレイの一例
Round(1) : State(h=12, g=0) -> Action=adventure
Round(2) : State(h=11, g=10) -> Action=adventure
Round(3) : State(h=9, g=30) -> Action=save
Round(4) : State(h=8, g=30) -> Action=investment
Round(5) : State(h=5, g=45) -> Action=investment
Final: h=2, g=67
  • とりあえず最初は adventure がいい。→⭕️
  • 死にかけ (例：3ターン目行動選択時点で残りhealthが4) の時はひたすらsaveするのが最適。→⭕️
  • goldが60より大きい時はinvestmentの方が良い行動→❌

上の例だと、Round(3)もしくは(4)はまだ"adventure"を選んだ方がいいのでは？
全体的に、かなり上手にプレイしてくれますが過剰に死亡を避ける傾向があるように見えます。

これについて、パラメータを色々振ってみた時に、DECAY_RATEを低め(あまりランダムに選ばない)の設定にするとほとんど学習が進まなかったという結果が得られました。
今回のケースでは、ちょっと間違えたら死亡してしまうが報酬が高い選択肢をいかに学習するかが肝になっている気がします。

まとめ

まだまだ改善の余地はありますが、強化学習を実行することができました🙌

Discussion