Shapashで分類モデルを可視化する(Titanic)
この記事について
下記で、不動産価格予測(回帰モデル)を可視化しました。
上記では、可視化を詳しくは扱っていなかったので、
- Jupyter上でのインラインでの可視化について扱っていきたいと思います
- 題材は、前回が回帰だったので、今回は分類(Titanic)にしてみたいと思います。
具体的には、Shapashで下記のような作図を行います。
まずは準備
前回と同じように、データをロードし、機械学習モデルを作成してから、可視化を進めます。
機械学習モデルの作成
# Import
import pandas as pd
from category_encoders import OrdinalEncoder
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from shapash.data.data_loader import data_loading
from category_encoders import OrdinalEncoder
# 今回は分類なのでtitanicをロードします
titanic_df, titanic_dict = data_loading('titanic')
# Xとyに分けます
y_df=titanic_df['Survived'].to_frame()
X_df=titanic_df[titanic_df.columns.difference(['Survived'])]
# カテゴリー値を探して
categorical_features = [col for col in X_df.columns if X_df[col].dtype == 'object']
# エンコードしておきます
encoder = OrdinalEncoder(
cols=categorical_features,
handle_unknown='ignore',
return_df=True).fit(X_df)
X_df=encoder.transform(X_df)
# 学習用・予測用にデータ分離し
Xtrain, Xtest, ytrain, ytest = train_test_split(X_df, y_df, train_size=0.75, random_state=7)
# Xgbで学習します
clf = XGBClassifier(n_estimators=200,min_child_weight=2).fit(Xtrain,ytrain)
# 予測も作っておきます
y_pred = pd.DataFrame(clf.predict(Xtest),columns=['pred'],index=Xtest.index).astype(int)
Explainerの作成(可視化の準備)
前回と同様に、SmartExplainerに対して、
- features_dict
- 特徴量(列名)に対するデータの説明をdictで渡します
- label_dict
- 予測対象は今回分類なので、結果が0:Death、1:Survivalで表現されています。
- 0,1のままで扱っても良いのですが、labelが振られていたほうが見やすいですので、ここで指定しておきます
from shapash.explainer.smart_explainer import SmartExplainer
response_dict = {0: 'Death', 1:' Survival'}
xpl = SmartExplainer(
features_dict=titanic_dict, # 特徴量の説明を指定
label_dict=response_dict # 結果ラベルを指定
)
そして、前回と同じように、説明変数、分類モデル、前処理に利用したエンコーダ、予測結果を指定してコンパイルします。
xpl.compile(
x=Xtest,
model=clf,
preprocessing=encoder,
y_pred=y_pred
)
モデルの可視化
年齢と生存
xpl.plot.contribution_plot(col='Age',label='Survival')
出来上がったモデルについて、年齢と生存の関係性を可視化してみたいと思います。
- 横軸に、乗客の年齢をとり
- 縦軸に、予測の貢献度(Contribution)を取ります[1]
- そして、予測モデルで算出した生存確率(Predicted Proba)が色で示されます(赤が生存確率が高い)[2]
とりあえず、言えそうなことは、現状の予測モデルは、
| 年代 | 予測の貢献度(縦軸)について | 予測される生存確率[2:1](色)について |
|---|---|---|
| 10歳以下 | 生存という予測に対し、正の貢献 (生存しやすい) |
赤が多く生存確率が高い一方、一部のデータ (8~10の青のデータ)に関しては 年齢以外の要因で亡くなる可能性が高い |
| 10歳~40歳 | このセグメントは年齢が、 生死の予測に対し説明性が低い (年齢だけでは生死判断が難しい) |
赤、青が混在しており、生死は他の要因で決まる |
| 40歳以下 | 生存という予測に対し、負の貢献 (亡くなりやすい) |
赤のデータは見られるものの60歳以降は青となり、 亡くなる可能性が高い |
10歳以下のセグメントの生死の要因
10歳以下のセグメントの生死の要因を確認してきたいと思います。
下記のようにZoomし、マウスオーバでデータのIDを確認することができます。
ここでは、下記の2つのデータに着目してみたいと思います
| id | 年齢 | 予測される生存確率[2:2] |
|---|---|---|
| 51 | 7歳 | 0.00108 |
| 298 | 2歳 | 0.9915 |
id:51(7歳)の確認
xpl.plot.local_plot(index=51)
- 年齢=7歳は、生存確率[2:3]に対して、貢献しています。
- 一方で、「Relatives such as brother or wife(兄弟や妻などの親戚)」が、4と突出しています。
- 実際の因果は別の方法含め正確に検討する必要がありますが、モデル上は、この4という数字が生存確率[2:4]を大きく引き下げています。

id:298(2歳)の確認
下記の要素により、生存確率[2:5]が高いと予測されています。
- 年齢が2歳であること
- Ticketのクラスが、First classであること。(ちなみに、上記のid:51はThird class)
- 性別が、女性であること
xpl.plot.local_plot(index=298)

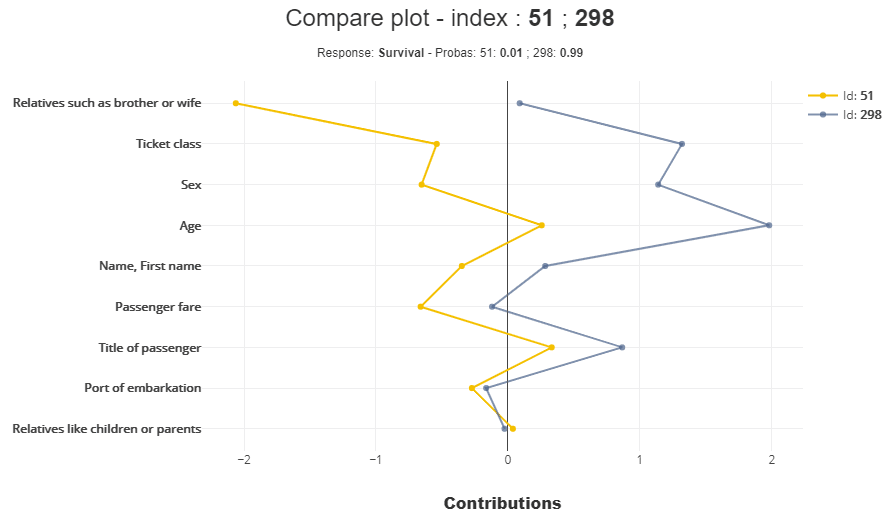
両者の比較
xpl.plot.compare_plot(index=[51,206])
上記の議論で、作成したモデルがどういったロジックで生存確率[2:6]を決めているか?雰囲気は理解出来たとおもうのですが、両者を比較しておこうと思います。
こうみてみると、「Relatives such as brother or wife(兄弟や妻などの親戚)」の影響が大きいです。
「Relatives such as brother or wife」の軸で確認
xpl.plot.contribution_plot(
"Relatives such as brother or wife",
violin_maxf=1 #デフォルト10以下でViolin_plotになるが見ずらいので1に設定
)
やはり、この数値が大きいほうが、
- 死亡率に対する貢献(説明性)が高く(縦軸で下の方)、生存確率[2:7]が低い(色が青)という結果になります。
ただ、データが少数なので、本当に上記の解釈で良いかはもう少し議論が必要かもしれません。
(データの作成過程や選択バイアス等の再確認)

Ticket classでの比較
xpl.plot.contribution_plot(col='Ticket class',label='Survival')
上記で確認してきたとおり、
- 生存に対して、first_class,second_classというのは説明の貢献度が高いです。(生存しやすい)
- 一方で、死亡に対しては、first,second,thirdだからということはなく、ほかの要因と合わせて死亡確率[2:8]が高くなる
といった状況でしょう。

まとめ
前回とは異なる分類について、jupyterにinlineする形で可視化を行い、作成したモデルの「見える化」を行いました。
データの解釈については、若干怪しいところはあったかもしれませんが、、、
Shapashを使うことで、ほぼ1行で様々な軸の可視化が行える点は、ご理解いただけたかと思います。
コメント等あれば頂ければ幸いです。
Discussion