😎

FrontISTR(EasyISTR)：熱-構造連成解析（円柱冷却中の応力と残留応力）

2022/11/18に公開

CAE

1.概要

この記事はFrontISTRとEasyISTR（参考[1,2]）を使用して，図1-1，1-2のような熱-構造連成解析を実施した際の記録です．円柱状の鉄の棒を500℃から冷却したときに冷却中に発生する応力と冷却完了後の残留応力を計算しました．図1-1には温度履歴のアニメーションを示し，図1-2には応力の代表値としてMises応力の履歴アニメーションを示しています（図1-1，図1-2では円柱断面を表示）．

図1-1. 温度履歴アニメーション

図1-2. Mises応力の履歴アニメーション

解析モチベーションとしては，500℃に加熱された鉄の棒を常温（20℃）の水に漬けて冷却したときに下記を数値解析で知りたい，というものです（図1-3）．

冷却中に発生する応力分布はどうなっているのか？
冷却中に材料が降伏する場合は残留応力の分布はどうなっているのか？

図1-3. 解析モチベーション

この記事では，伝熱解析と構造解析の連成解析を実施していますが，その連成方法は弱連成解析です．伝熱解析を先に実施しておき，伝熱解析で求めた温度履歴を参照しながら熱応力解析を実施してます．弱連成解析で十分な理由については，簡単にですが後述します．伝熱解析の実施方法は以前書いた記事（参考[3]）で説明したのでこの記事では説明しません．

また，解析に使用したメッシュはSalome-Mecaで作成しました．メッシュの作成方法も以前書いた記事（参考[4]）で説明したのでこの記事では説明しません．

伝熱解析の設定やメッシュの切り方は以前書いた記事と全く同じものではありませんが，両者とも殆ど同じやり方で実施できると思います．以前書いた記事もこの記事も，なるべく間違いの無いように努めていますが，より正確な情報が知りたい場合は各ソフトウェアの公式ヘルプを参照ください．

本記事では下記の流れで解析方法とその結果について説明していきます．また，解析ではmm，ton，secの単位系で行っていますが，見にくい人も居ると思うので，MKS(SI)単位系の値もなるべく併記しています．

2節で主な解析条件について説明
3節でプリソフト（EasyISTR）を使用した解析設定方法を説明
4節で解析結果について説明

2.主な解析条件

2-1.使用した物性値と材料モデル

今回の解析では図2-1に示すような物性値を使用しました．各物性値は常温における純鉄の一般的な値です．今回の解析では簡単のために各物性値の温度依存性を考慮していません．今回の問題では500℃～常温（20℃）の範囲で温度が変化するので，正確な計算がしたい場合は各物性値に温度依存性を持たせた方が良いです．物性値によっては500℃と20℃では倍近く変わるものもあります．

図2-1. 使用した物性値：純鉄の常温における値

また，500℃近くまで加熱された鉄の棒を水に漬けて冷却した場合，鉄の棒の寸法などにもよりますが，多くの場合，冷却中に発生する温度偏差起因の熱応力で，材料は塑性変形することが広く一般的に知られています．よって，今回は塑性変形に関わる物性値も使用し，解析自体も材料非線形性を考慮して実施しています．使用した塑性変形の材料モデルは下記です．

降伏関数：Misesの降伏関数
硬化モデル：線形移動硬化則

降伏関数には色々種類がありますが，金属材料の場合，Misesの降伏条件に従う場合が多く，多くの場合よい近似となります．よって，今回はMisesの降伏関数を使用しています．

硬化モデルとして移動硬化則を選択した根拠は下記2点になります．

多くの鋼材は等方硬化よりも移動硬化が強く出る
冷却中と冷却完了後で応力の向き（正負）が反転する

ただ，色々な文献を見てみると，純鉄の場合，硬化係数が比較的小さいのと，今回考えている状況では10%を超えるような大きな塑性ひずみは発生しないので，どの硬化モデルを選択しようが解析結果に及ぼす影響は小さいです．よって，今回の場合は，硬化モデルの選択はあまり神経質にならなくて良さそうです．

2-2.メッシュ情報

解析には図2-2のようなメッシュを使用しました．対称境界条件を利用し，円柱の一部分のみ計算してます．考えているのは半径が50mmの円柱で，モデル規模は1万節点程度です．

図2-2. メッシュ情報

2-3.境界条件

伝熱解析で使用した熱的境界条件は下記です．円柱側面以外に断熱境界条件を設定し，無限に長い円柱の1/4部分だけを切り出して計算しています．

初期温度：全節点で500℃
円柱側面以外：断熱境界条件（無限に長い円柱を想定）
円柱側面：熱伝達境界条件
- 熱伝達係数： $5.0 \ [\rm mW/(mm^2 \cdot {}^\circ\mathrm{C})] = 5000 \ [W/(m^2 \cdot {}^\circ\mathrm{C})]$
- 雰囲気温度： $20 \ [{}^\circ\mathrm{C}]$

構造解析で使用した機械的境界条件は下記です．対称面として変位拘束を施したのは，円柱の内部側面と円柱の上面です．円柱の底面には変位拘束を設定していません．つまり，構造解析では有限の長さを持った円柱のうち，1/8部分を切り出して計算しています（図2-3）．

全節点：温度境界条件（伝熱解析の温度出力結果を逐次参照）
対称面の節点：変位境界条件（変位拘束）

図2-3. 構造解析の対称境界条件

伝熱解析と構造解析で境界条件の取り扱い方が違い，考えている円柱の長さが異なります．これは，構造解析では「無限に長い円柱」のような境界条件の設定ができないためです．仮に，円柱底面に対しても変位拘束を設定すると，計算している円柱の高さに応じた（今回の問題設定にそぐわないような）過剰な熱応力が円柱の高さ方向に生じます．

それならば伝熱解析の方も「無限に長い円柱」として計算しなければ良いではないかと思う方もいるかもしれませんが，それはそれで伝熱現象の対称性が崩れて解析設定ミスに気が付きにくくなります．今回の解析は「現象を再現する本気の解析」というより，意図した解析がきちんと行えているかを確認する意味合いが強いです．これは，私がFrontISTRを使い始めて数週間しか経っておらず，その仕様などを詳しく知らない所も多いためです．（この記事の内容は単なる趣味の解析です．）

また，今回は簡易的な結果整理しかしていませんが，解析結果は最も対称性の高い円柱上面（対称境界を設定し変位拘束している面）に対して主に行います．解析上，円柱上面に対応する面は，現実の鉄の棒の高さ方向のちょうど中心にあたり，物理現象を最も代表していると推定されるためです．

2-4.連成解析

今回の解析は，伝熱解析と構造解析の弱連成解析です．まず先に伝熱解析を実施し，円柱の全節点における温度履歴を構造解析とは独立して求めておきます．そして，構造解析では伝熱解析で求めた温度履歴を参照しながら熱応力を進めています．今回考えている現象のように，熱応力の結果として生じる熱変形によって伝熱解析の境界条件が大きく変化しないような状況のとき，弱連成解析でも十分良い近似となります．

今回の伝熱解析全体をSTEP0としたとき，このSTEP0は60個のサブステップに分けられます（初期ステップも含めると61個）．この60個の各サブステップにおいて温度が出力されています．このサブステップは時刻の進行に対応しますが，各サブステップ間の時間刻みは一定とは限りません．時間刻み一定とも設定できますし，一定にしないようにも設定できます．60個のサブステップが今回は存在しますが，この60という値は今回たまたまこういう値だっただけで，特別な意味はありません．そして，構造解析の境界条件も60個のサブステップに分けて，各サブステップで伝熱解析の温度結果を温度境界条件として逐次解析していきました（図2-4）．

図2-4. 連成解析実施イメージ

今回は伝熱解析で出力した60個のサブステップの結果全てを使用しました．ただ，構造解析における計算時間を短縮したいなどの動機から，何サブステップおきに伝熱解析の結果を利用するかを指定することもできます．（温度履歴のスキップ）

2-5.その他の解析設定

この節では2-1 ~ 2-4節の内容には該当しないものの，重要と思われる解析設定について備忘録として残しておきます．

今回は非定常熱伝導解析（熱伝導：動解析）の設定を下記のようにしました（!HEATの設定）．常温まで冷えるのに，結構時間がかかるかな思い，計算時間（ETIME）は長めにとりましたが，解析結果の温度履歴を見ると200.0[sec]くらいでも問題なさそうでした．

自動時間増分設定機能使用
初期時間増分（DT）：0.01 [sec]
計算時間（ETIME）：400.0 [sec]
最小時間増分（DTMIN）：0.001 [sec]
1サブステップあたりの許容温度変化（DELTMX）：20.0 [℃]
非線形最大反復数（ITMAX）：20 [回]
収束判定値（EPS）： $1.0 \times 10^{-6}$ [-]

非線形構造解析（非線形静解析）の設定は下記のようにしました（!STEPの設定）．最大反復回数（MAXITER）はやや大きめにとりましたが，解析ログを見る限り10回以下でも問題なさそうでした．サブステップ数を60回としているのは，熱伝導解析の結果が60個のサブステップに分けられていたためです．熱伝導解析の全ての計算ステップの温度履歴を参照して，構造解析をしたかったため，構造解析のサブステップ数を60としました．

最大反復回数（MAXITER）：20 [回]
打ち切り誤差（CONVERG）： $1.0 \times 10^{-6}$ [-]
サブステップ数（SUBSTEPS）：60 [個]

線形ソルバーの設定は熱解析と構造解析で同じ設定で計算しました．同じ設定にしている根拠はあまりありません．反復回数（NIER）は大きめに設定していましたが，解析ログを見ると500回くらいで収束していたので，1000回くらいの値でも問題なさそうです．また，試していませんが，今回の解析規模くらいであれば直接法を使った方が速く計算が終わったかもしれません．

数値解法（METHOD）：CG法（反復法）
前処理手法（PRECOND）：SSOR
反復回数（NIER）：20000 [回]
打ち切り誤差（RESID）： $1.0 \times 10^{-6}$ [-]

並列計算の設定は下記のようにしました．今回の構造解析は非線形計算を60計算ステップ行っていますが，2並列の計算で約15分程度かかりました．これは私が使っているPCが5万円くらいで買った安物のPCだからだと思います．良いコンピュータを使っている人はもっと早く計算が終わると思います．

並列数（領域分割数）：2
スレッド数：1

3.EasyISTRを使用した解析設定

3節ではEasyISTRでFrontISTRのインプットファイルを作成する手順について説明します．伝熱解析の実施手順は以前書いた記事(参考[3])で説明したので省略します．ここで説明するのは構造解析側での手順です．

また，EasyISTRの公式マニュアルでは伝熱解析を実施したフォルダと同じフォルダで構造解析を実施する方法を説明していますが，ここでは，伝熱解析と構造解析で解析フォルダを分けて解析する方法をとります．同じフォルダで解析を実施すると，ParaViewで読み込む結果ファイルが上書きされてしまい，私の場合はこれを避けたかったためです．

また，下記4点は恐らくEasyISTR上からは実施できない項目になるので注意してください．

メッシュファイルを伝熱解析のフォルダから構造解析のフォルダへコピー：FistModel.msh
伝熱解析の結果ファイル（FistrModel_temp.res.***）を構造解析のフォルダへコピー
参照温度の設定(!REFTEMP)
並列計算実行時は並列計算用のメッシュ分割をした後に，再度，伝熱解析の結果ファイル（FistrModel_temp.res.***）を構造解析のフォルダへコピー

伝熱解析の結果ファイル（FistrModel_temp.res.***）を2回コピーしているのは，EasyISTR上から並列計算用のメッシュ分割を実施すると，結果ファイル(resファイル)が消去される仕様になっているためです．まだ，試していませんが例えば下記のようなことを行えばコピーの手間を省けるのではないかと思っています．1つ目のやり方はFrontISTRのマニュアルを読み込めていないので，実際にできるかどうか自信がありません．

伝熱解析の結果ファイルを構造解析のフォルダへコピーするのではなく，構造解析とは別のフォルダにある伝熱解析の結果ファイルへの相対パスまたは絶対パスを記述する．
並列計算用のメッシュ分割はEasyISTR上から実施するのではなく，コンソール画面から並列計算用のメッシュ分割を実施する（hecmw_part1をコマンドで実行）．

3-1.作業ディレクトリの設定

まずは作業ディレクトリを設定します．作業ディレクトリの中に予め伝熱解析で使用したメッシュファイル（FistrModel.msh）を入れておきます．手順は下記です（図3-1）．メッシュファイルのコピーはEasyISTR上からは実施できないので，マウス操作またはコマンドで実施してください．

作業ディレクトリを作成：今回は「21_cylinder_struct」というディレクトリを作成
作業ディレクトリとするディレクトリに伝熱解析で使用したメッシュファイルをコピーする：今回は「21_cylinder_struct」というディレクトリに「FistrModel.msh」をコピー
「選択dirを作業folderに設定」をクリック

図3-1. 作業ディレクトリの設定

3-2.解析タイプの選択

次は解析タイプを選択します．今回は弾塑性解析を実施したので非線形静解析を選択します．手順は下記です（図3-2）．

解析の種類を選択
解析の種類から「非線形静解析」を選択
「設定」をクリックし設定を保存

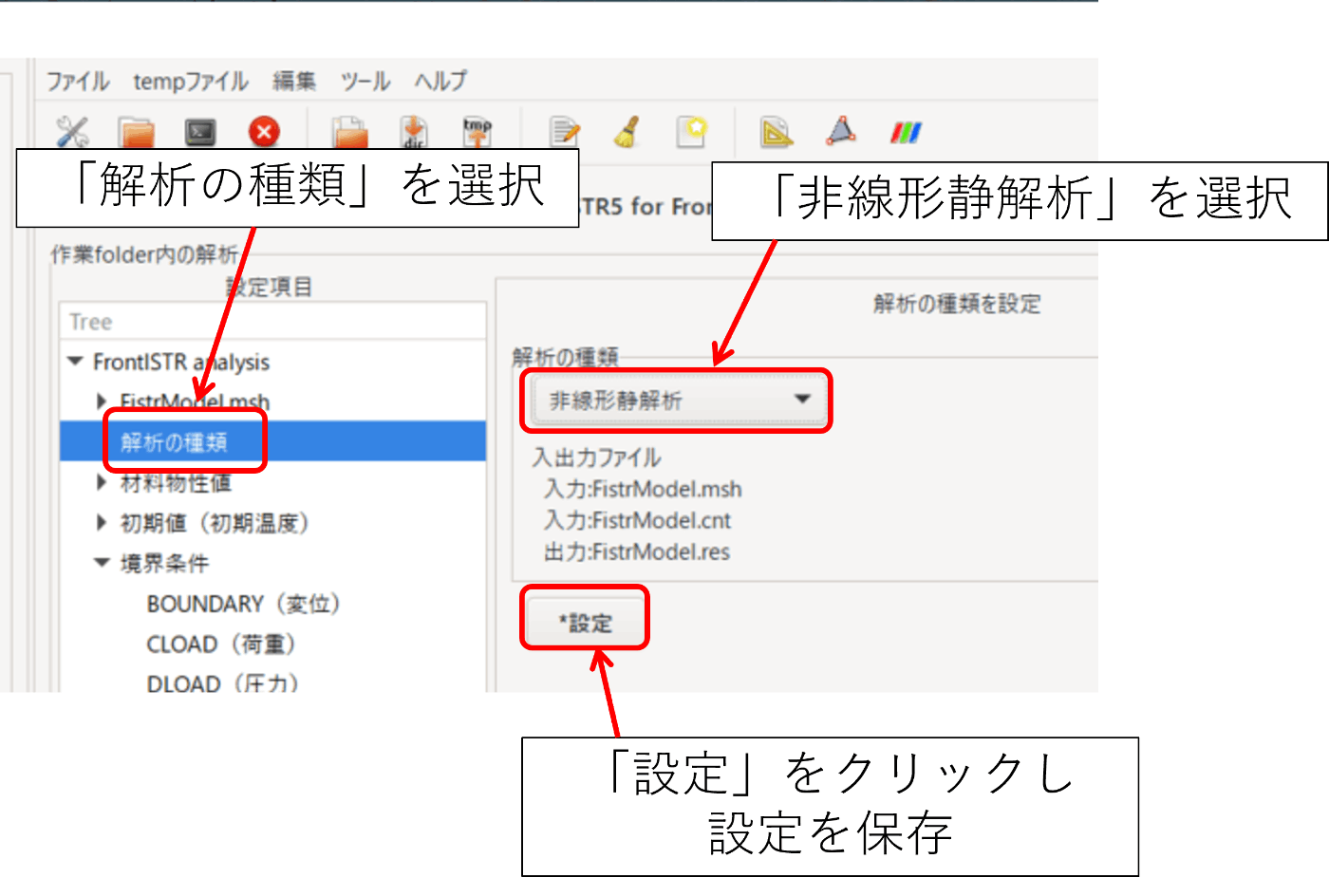
図3-2. 解析タイプの選択

3-3.材料特性の割り当て

材料特性を割り当てる要素集合を選択し，材料モデルの選択と塑性変形に関わる物性値を入力します．手順は下記です（図3-3）．

材料特性を割り当てる要素集合を選択：今回は「elem_all」（全要素集合）を選択
材料名を選択：今回は「Steel」を選択
材料モデルから「PLASTIC」を選択
降伏条件から「MISES」を選択
硬化則から「KINEMATIC」を選択
「mat_data作成・編集」をクリックし，初期降伏応力と線形移動硬化係数を入力
「設定」をクリックし設定を保存

図3-3. 材料特性の割り当て

3-4.境界条件の設定

境界条件の設定方法について説明します．設定する項目は「初期温度」，「変位境界条件」，「温度境界条件」の3つです．初期温度については伝熱解析で使用したメッシュファイルをコピーしてきた場合は，メッシュファイルの中に初期温度が既に記入されているはずなので改めて設定し直す必要はありません．ここでは，初期温度の設定についても念のため確認してきます（図3-4）．

初期温度を設定する節点集合を選択：今回は「node_all」を選択
初期温度を確認：今回は「500℃」が入力済み

図3-4. 初期温度の確認

次は対称面を設定するために変位境界条件の設定をします．変位境界条件を設定する節点集合を選択します．手順は下記です（図3-5）．

境界条件の中から「BOUNDARY（変位）」を選択
変位境界条件を設定する節点集合を選択して右へ移動：今回は「node_inside_xz_plane」，「node_inside_yz_plane」，「node_top」の3つの節点集合を選択
「設定」をクリックし設定を保存

図3-5. 変位境界を設定する節点集合の選択

対称面を設定するために，具体来な変位境界条件の値（今回は変位固定）を入力していきます．まずは，XZ平面に属する節点集合にY方向の変位拘束を施します．手順は下記です（図3-6）．

XZ平面に属する節点集合を選択：今回は「node_inside_xz_plane」を選択
Y方向の変位値を入力：今回は変位拘束のためY方向に「0」を入力
「設定」をクリックし設定を保存

図3-6. 対称面の設定：XZ平面に属する節点集合に対するY方向の変位拘束

次は，YZ平面に属する節点集合に対しX方向の変位拘束を施します．手順は下記です（図3-7）．

YZ平面に属する節点集合を選択：今回は「node_inside_yz_plane」を選択
X方向の変位値を入力：今回は変位拘束のためX方向に「0」を入力
「設定」をクリックし設定を保存

図3-7. 対称面の設定：YZ平面に属する節点集合に対するX方向の変位拘束

次は，円柱上面（XY平面に平行な平面）の節点集合に対しZ方向の変位拘束を施します．手順は下記です（図3-8）．

円柱上面の節点集合を選択：今回は「node_top」を選択
Z方向の変位値を入力：今回は変位拘束のためZ方向に「0」を入力

図3-8. 対称面の設定：円柱上面の節点集合に対するZ方向の変位拘束

次は，温度境界条件の設定をします．熱伝導解析から出力された温度の結果ファイル（FistrModel_temp.res.***）を構造解析で参照するための設定です．ここの手順を完了させるためには，マウス操作やコマンドで結果ファイル（FistrModel_temp.res.***）を構造解析を実行するフォルダへコピーしておく必要があります．コピーの操作自体はEasyISTR上からはできないと思います．手順は下記になります（図3-9, 3-10）．

境界条件の項目の中から「TEMPERATURE（温度）」を選択
熱伝導解析の温度結果を参照させる節点集合を選択して右へ移動：今回の場合は「node_all」（全節点集合）を右へ移動
「設定」をクリックし設定を保存

図3-9. 熱伝導解析の温度結果を参照させる節点集合の選択

温度境界条件を設定する節点集合を選択：今回は「node_all」（全節点集合）を選択
「熱伝導解析結果を使う」にチェック
熱解析結果の全step数（READRESULT）を入力：今回は「60」を入力
熱解析結果の計算開始stepNo(SSTEP)を入力：今回は「1」を入力
熱解析の読み込み間隔（INTERVAL）を入力：今回は「1」を入力（全ての温度結果を参照）
温度の結果ファイルをここまでにコピーしておかないと，設定を保存しようとしても，エラーメッセージが出てきて先に進めないので，ここまでに温度の結果ファイルをコピーしておく．
「設定」をクリックし設定を保存

図3-10. 熱伝導解析の温度結果を参照させるための設定

3-5.ステップ（!STEP）の設定

前節で熱伝導解析の温度結果を参照させるための設定をしましたが，「!STEP」のカード部分でも温度参照のための設定をする必要があります．「!STEP」のカード内でサブステップ数を明示的に指定しないと，サブステップの数が1になってしまい，温度の履歴に応じた構造解析が実施できず，意図した解析をしたことになりません．また，「!STEP」のカード内では非線形計算の収束判定値や最大反復回数も指定します．

まずはステップそのものを明示的に作成します．手順は下記です（図3-11）．

「ステップ解析」を選択
「追加」を1回だけクリックし境界条件のセットとなるステップを作成：STEP0の作成
「設定」をクリックし設定を保存

図3-11. ステップの明示的作成

次にサブステップ数や収束判定値などを指定します．手順は下記です（図3-12）．

先ほど作成した「STEP0」を選択
収束判定値（CONVERG）を入力：今回は1e-6とした
サブステップ数（SUBSTEPS）を入力：今回は温度履歴のサブステップ数に合わせて「60」を入力
最大反復回数（MAXITER）を入力：今回は20とした
「STEP0」に対して設定する境界条件を選択して右へ移動．今回の場合は下記4つの境界条件
- 変位境界条件：XZ平面に属する節点に対する対称境界条件（円柱内部節点）
- 変位境界条件：YZ平面に属する節点に対する対称境界条件（円柱内部節点）
- 変位境界条件：円柱上部の節点に対する対称境界条件
- 温度境界条件：熱伝導解析結果の参照（全節点）

図3-12. ステップの設定：サブステップ数の指定と収束判定値などの設定

3-6.参照温度の設定

ここでは熱応力解析で使用する参照温度（!REFTEMP）の設定をします．参照温度（!REFTEMP）を明示的に指定しない場合はデフォルト値が自動的に採用され，その値は「0」です．使用している単位系にもよりますが，多くの場合，0℃か0Kになると思います．今回は参照温度として500℃（初期温度）を指定します．

参照温度を明示的に指定しないと，1つ目のサブステップにおいてのみ，等方的な引張応力が解析結果として出力されてしまいました．恐らく等方的な熱ひずみがそのまま応力値に反映されたものと推定されるような値でした（本来出るはずの熱応力よりも遥かに大きな応力値で $\sigma_{xx}，\sigma_{yy}，\sigma_{zz}$ が全てほぼ同じ値）．これは不自然な（意図しない）解析結果です．2つ目のサブステップ以降はこのような不自然な等方的引張応力は消えました．

等方的な応力（応力の静水圧成分）は塑性変形に効かないので，残留応力だけに注目する場合はあまり気にしなくても良い解析設定項目かもしれません．ただ，応力の履歴をグラフ化するときに，1つ目のサブステップだけ特異な応力が出力されていては気持ち悪いので，私は参照温度を明示的に指定しました．

そして，参照温度（!REFTEMP）の設定はEasyISTR上からできないので，*.cntファイルに自分で直接記入する必要があります．ここではテキストエディタの実行ファイルへのパスをEasyISTRの設定ファイルに記入している場合の手順を説明します．パスの設定をしていない人は，*.cntファイルを適当なテキストエディタで開いて編集してください．

パスの設定をしている場合の手順は下記です（図3-13）．「!REFTEMP」を記述する位置は*.cntファイルの中であれば恐らくどこでも良いですが，私は温度境界条件を指定している位置の近くに追記しておきました．

「編集」から「cnt，mshファイル編集」を選択
*.cntファイルに「!REFTEMP」を指定：今回は「500.0」を指定
「tempファイル」から「保存(temp->dir)」を選択し，tempフォルダの中の*.cntファイルの内容を作業dir内の*.cntファイルへと反映させる．

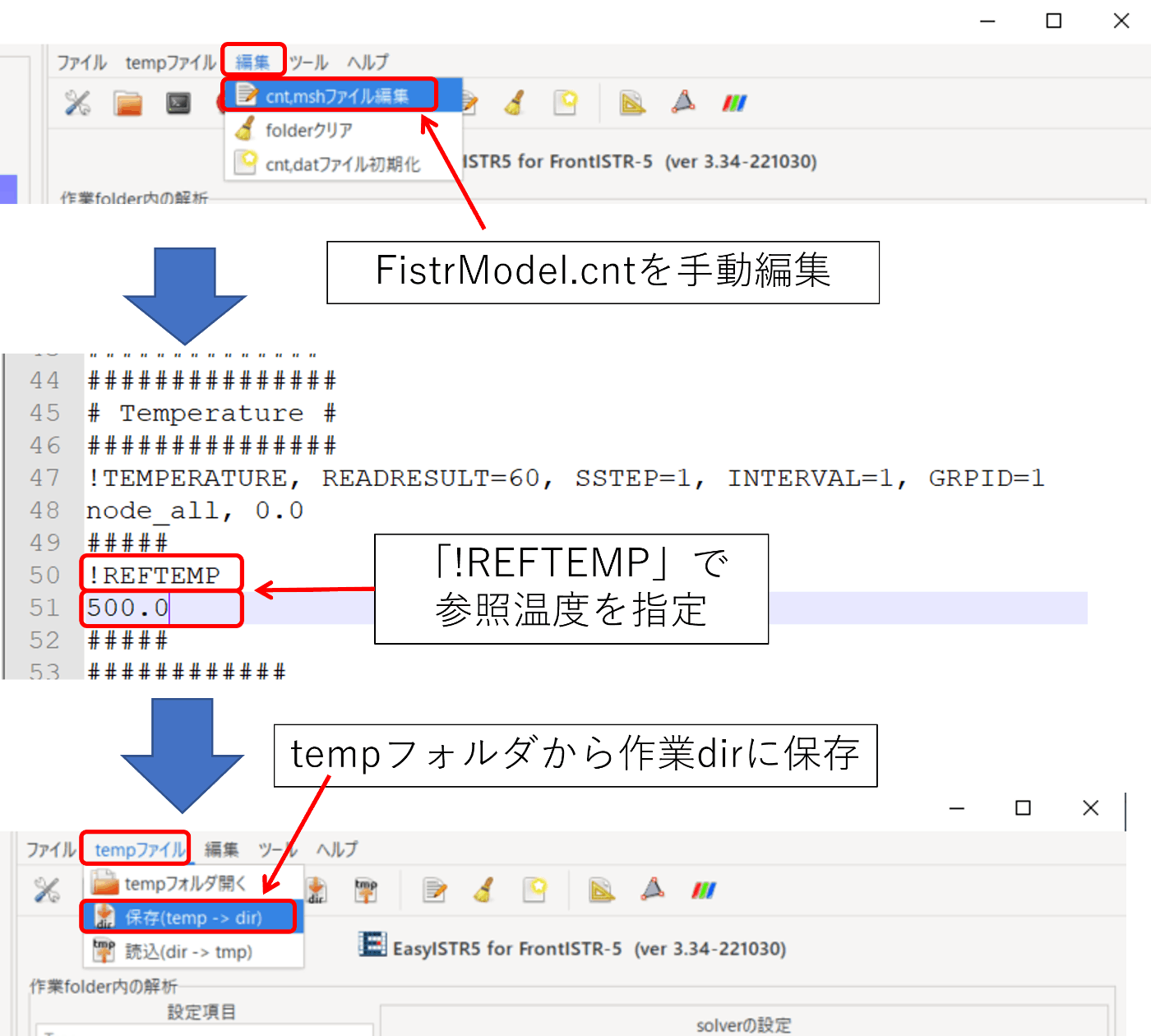
図3-13. 参照温度（!REFTEMP）の明示的指定

3-7.その他の解析設定

ここでは線形ソルバーの設定と並列計算の並列数の設定手順について説明します．まずは線形ソルバーの設定です．手順は下記です（図3-14）．

「線形solver」を選択
解法（METHOD）を選択：今回は「CG法」を選択
前処理手法（PRECOND）を指定：今回は「1」を指定（SSORを指定したことになる）
反復回数（NIER）を指定：今回は20000を指定（安全目に少し大きめの値を指定）
打ち切り誤差（RESID）を指定：今回は「1.0e-6」と指定
「設定」をクリックし設定を保存

図3-14. 線形ソルバーの設定

最後に並列計算の設定をし，解析を実行します．手順は下記です（図3-15）．EasyISTR上から並列計算用のメッシュを作成すると，温度の結果ファイル（resファイル）が消えるので，resファイルを作業ディレクトリへ再度コピーします．

「solver」を選択
「並列計算する」にチェックを入れる
並列数を入力：今回は「2」を入力（2並列）
「メッシュ分割」をクリックし並列計算用のメッシュ作成
EasyISTR上から並列計算用のメッシュを作成すると温度の結果ファイル（resファイル）が消えるので，resファイルを作業ディレクトリへ再度コピー．
結果出力頻度を入力：今回は「1」を入力（全てのサブステップの結果を出力）
スレッド数を入力：今回は「1」を入力
「設定」をクリックし設定を保存し解析実行

図3-15. 並列数の指定と解析実行

4.解析結果

ここでは，解析結果について簡単に整理します．図4-1は温度履歴のコンター図で，図4-2はMises応力の履歴のコンター図です．円柱の表面から温度が低下していき，円柱表面で最も強いMises応力が発生していることが分かります．また，冷却が完了し円柱全体が均一になった状態においてもMises応力が発生していることも分かります．これは冷却中に降伏応力を超える応力が発生し，材料が塑性変形したためです．

図4-1. 温度履歴アニメーション

図4-2. Mises応力の履歴アニメーション

次は，物理現象を一番代表していると思われる，円柱の上面に注目して計算結果を整理していきます．図4-3の青く塗った面が注目している面です．温度，Mises応力，高さ方向応力，周方向応力，半径方向応力について整理しました．今回は，主応力の結果までは整理していませんが，今回のように割と対称性の高い問題では応力の向きが割とはっきりしているので，主応力の結果整理は省略しました．

図4-3. 計算結果を整理した面

図4-4に円柱中心と側面の温度履歴を示し，図4-5に円柱中心と側面のMises応力の履歴を示しました．今回は初期降伏応力は温度によらず250[MPa]としました．円柱の中心部においては全時刻通して初期降伏応力以下の応力しか出ていないことが図4-2や図4-5から分かります．よって，今回の計算条件では塑性変形をするのは円柱の側面に近いところのみで，中心部付近は塑性変形をしないことが分かります．

今回は初期降伏応力を温度によらず250[MPa]としていましたが，初期降伏応力は高温ほど低い値を持ちます．鉄（鋼）といっても，色々と種類があるため一概には言えませんが，500℃と20℃では初期降伏応力は1/2~2/3程度違ってくるのが一般的です．Mises応力の大きさを見ると，円柱中心部において200[MPa]程度の大きさを持つ時刻があるため，初期降伏応力の温度依存性を考慮すると中心部も塑性変形を起こすことが予想されます．

図4-4. 円柱の中心と側面の温度履歴

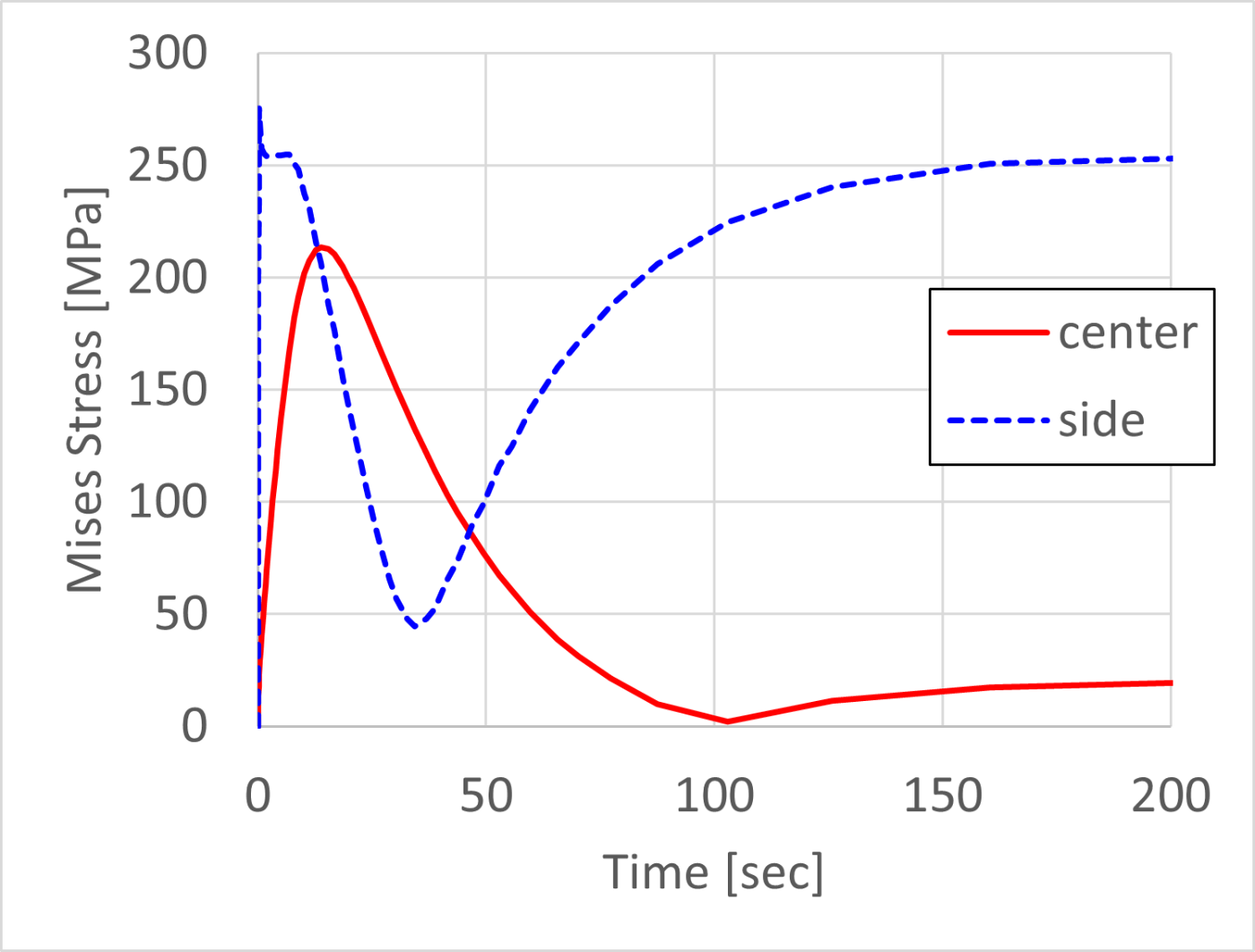
図4-5. 円柱の中心と側面のMises応力の履歴

次は高さ方向の応力履歴と周方向の応力履歴を見ていきます．図4-6に高さ方向の応力履歴を示し，図4-7に周方向の応力履歴を示しました．円柱側面の点における応力に注目すると，高さ方向の応力も周方向の応力も，冷却の初期段階においては引張の応力を示していますが，冷却が完了した段階においては圧縮の応力へと応力が反転していることが分かります．逆に，円柱の中心部の点においては，冷却の初期段階においては圧縮の応力を示していますが，冷却が完了した段階においては引張の応力へと応力が反転しています．

冷却の初期段階において，円柱の側面に近い所は円柱の中心に近い所に比べて，熱収縮で円柱の寸法が縮むためです．円柱の側面と中心は互いに拘束し合っているので，この熱収縮の度合い（熱ひずみの発生度合い）に応じて，円柱側面は引張の応力を示し，円柱の中心は圧縮の応力を示します．そして，円柱の側面では引張の応力が初期降伏応力を超えてしまい，引張の塑性変形を起こします．

塑性ひずみは冷却が完了して温度が均一になった状態においても残りますから，冷却完了後は，円柱側面の引張の塑性ひずみにより，円柱側面と円柱中心では寸法差が生じます．円柱側面と円柱中心は互いに拘束し合っていますから，この寸法差を修正する方向の応力が発生します．これが残留応力です．円柱側面には圧縮の残留応力が発生し，円柱中心には引張の残留応力が発生します．

図4-6. 高さ方向の応力履歴

図4-7. 周方向の応力履歴

次は半径方向の応力履歴を見ていきます．図4-8に半径方向の応力履歴を示しています．半径方向の応力については，リング状（車輪状）の構造物の穴に円柱を差し込むような状況（焼き嵌めに相当する状況）を考えると分かりやすいかもしれません．

冷却の初期段階において，円柱中心は圧縮の応力を受けています．冷却の初期段階において，円柱中心は円柱側面に比べて熱膨張しているので，この熱膨張を抑制する向きの応力，つまり圧縮応力が発生します（大局的に見ると円柱の中心方向の向きの力が発生）．円柱の側面は，冷却の初期段階において，円柱中心にくらべて熱収縮しているため，同じようにこの熱収縮を抑制する向きの応力が発生します．円柱側面に発生する圧縮応力を大局的に見ると，円柱の外周方向の向きの力が発生していることになります．

円柱側面の点において，冷却のごく初期段階（1 [sec]未満の領域において），すぐに応力が反転する方向へと向かっています．これは高さ方向の応力履歴や周方向の応力履歴と傾向が少し違います．円柱側面の点で応力反転の方向へ向かうタイミングを詳しく見てみると，ちょうど初期降伏応力を初めて超えるタイミングでした．高さ方向と周方向に引張側の塑性変形をした結果，それにつられて半径方向にマイナスの塑性ひずみが発生していることが原因であると推定されます．半径方向にマイナス方向の塑性ひずみが発生するとそれを修正する向きの引張応力が発生するためです．

図4-8. 半径方向の応力履歴

最後に冷却完了後における，半径方向の残留応力分布を見ていきます．図4-9に高さ方向の応力分布，周方向の応力分布，半径方向の応力分布，Mises応力の分布を示します．各方向の応力履歴の説明をある程度してしまったので，ここで語るべきことはあまりありませんが，円柱表面から10mm程度の領域（中心から40~50mmの領域）は圧縮応力が支配的であることが分かります．

今回は500℃まで加熱した円柱を水に漬けて冷却するような状況を考えているので，冷却中に発生する応力の履歴を直接測定するのは難しいと思います（500℃まで持つようなひずみゲージはあまり見たことがありませんし，水中にある円柱に対し非接触で応力測定するのは難しいのではないかと思います）．よって計算結果の妥当性を評価する際に，残留応力の分布が一つの手がかりとして使える可能性はあります．

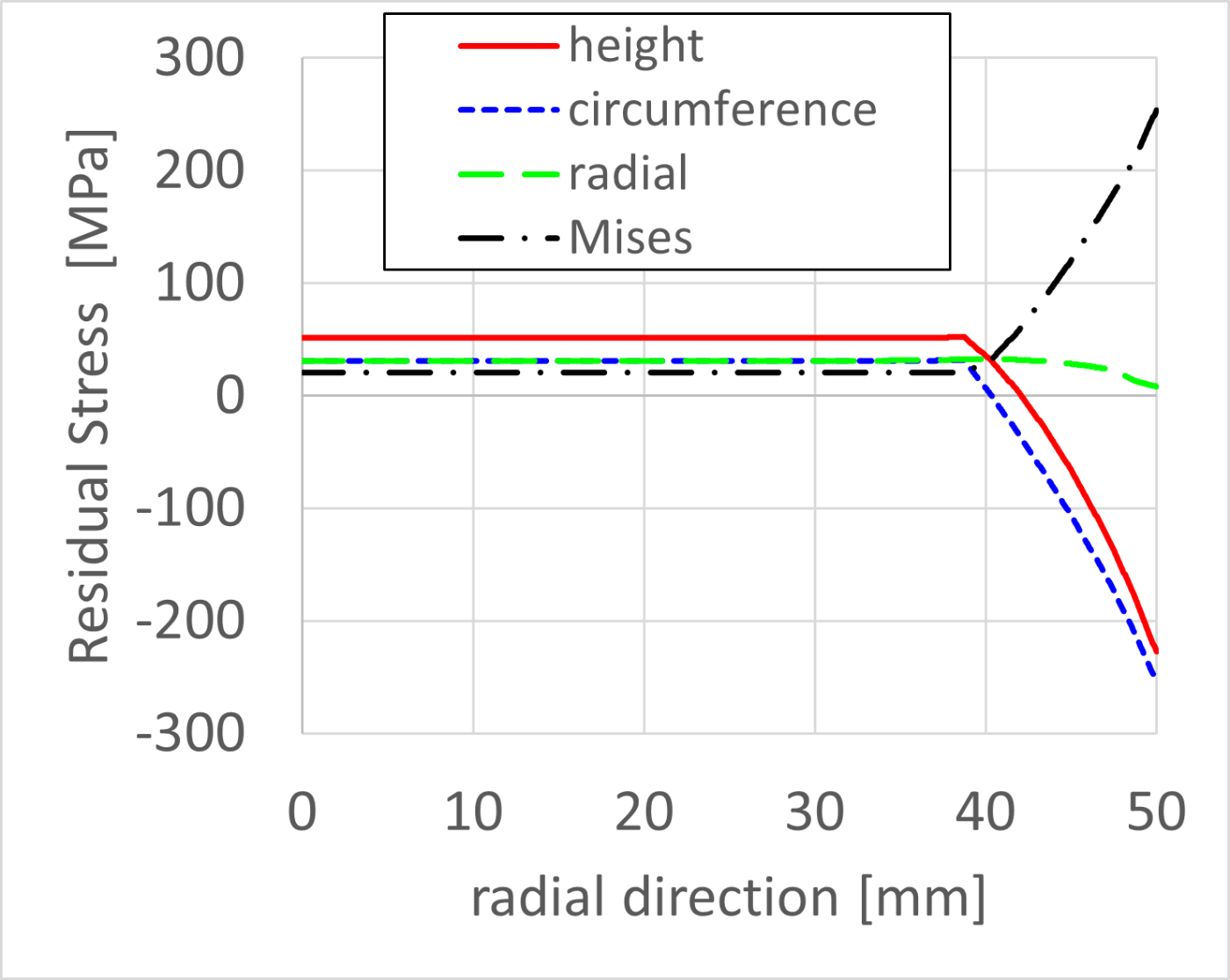
図4-9. 半径方向の残留応力分布

感想

FrontISTRで熱-構造連成解析を実現する際の設定方法が大まかに分かりました．FrontISTRのインプット形式にも段々と慣れてきたので，幾何非線形性や境界条件非線形性（接触問題）などについてもチャレンジしていこうと思います．

環境

・FrontISTR: ver.5.4 (MSMPI, Windows用バイナリ)
・EasyISTR: ver.3.34
・OS: Windows 10
・CPU: AMD Ryzen 5 3500U
・RAM: 8.0G

参考

[1]. FrontISTR：公式HP
[2]. EasyISTR：公式HP
[3]. FrontISTR(EasyISTR)：非定常伝熱解析（円柱の冷却）
[4]. Salome：任意の密度関数で不均一なメッシュを切る