年末ジャンボ宝くじは連番とバラのどちらが得か

概要

年末ジャンボ宝くじを買うときはバラで購入しましょう。

背景

今年も年末ジャンボ宝くじの季節がやってきました。1等は前後賞を併せて10億円です。昔は3億円くらいだったのにインフレしてますね。
https://www.takarakuji-official.jp/brand/jumbo/

購入時は「連番」「バラ」がありますが、どちらがよいのでしょう。
連番のほうが、1等が当せんしたときに前後賞もあるので期待値が上がるかと思っていましたが、バラの場合は前後賞のみ当せんする場合もあるので、結果的には変わらないように思えます。

「連番」と「バラ」

連番購入
組と番号の上5ケタまでは同一で、下1ケタの番号が0～9まで連続している10枚のセットです。
バラ購入
連続していない番号で、下1ケタの番号には0～9までの数字が入っている10枚のセットです。

参考: https://www.takarakuji-official.jp/brand/jumbo/guide/guide.html

しかし、果たして本当に差がないのでしょうか。
これを調べた先行研究はたぶん沢山ありますが、今回は自分でも検証してみたのでその結果をご紹介します。

前提

連番とバラの違いが出る部分のみを抽出し、理論的に当せん金の期待値を計算していきます。

• 1等、1等の前後賞のみを考慮し、その他は考慮しない。
• 組は考慮しない。
• 1枚購入した場合に1等が当せんする確率を $p=1/20,000,000$ とする。
• 1等の当せん金額を $w_1=700,000,000円$、1等の前後賞の当せん金額を $w_2=150,000,000円$ とする。
• 10枚1セットを購入単位とする。

1セット購入の場合

連番で購入したとき

連番で購入した場合、下1ケタ以外は同一になることから、1セット購入した場合の1等の当せん確率は $10p$ となります。
1等が当せんした場合、$8/10$ の確率で前後賞が2本当せんし、$2/10$ の確率で前後賞が1本のみ当せんします。

補足

例えば10-19の番号の10枚を購入していた場合を考えます。
当せん番号が購入範囲の境界である10または19のとき、前後賞の前か後ろのどちらかは範囲外の番号（9か20）になり、前後賞が1本のみ当せんとなります。
当せん番号が上記以外の11-18のとき、前後賞が前後ともに範囲内に収まるため2本とも当選します。

したがって、当せん金の期待値は

$$\begin{aligned} &\frac{8}{10} (w_1 + 2w_2) \cdot 10p + \frac{2}{10} (w_1 + w_2) \cdot 10p \\ &= (10w_1 + 18w_2)p \\ &= 10(w_1 + 2w_2)p - 2w_2p \end{aligned}$$

となります。
最後の等号は、後で比較しやすいように式変形しています。

バラで購入したとき

バラで購入した場合、1等の当せん確率は「10枚すべてが外れる場合の余事象の確率」ですので $1-(1-p)^{10}$ となります。
また前後賞は前と後を区別して考えると、それぞれ当せん確率は1等の場合と等しくなります。
したがって、当せん金の期待値は

$$(w_1 + 2w_2)(1-(1-p)^{10}) \approx 10(w_1 + 2w_2)p - 45(w_1 + 2w_2)p^2$$

となります。
ここで、$p \ll 1$ のとき $(1-p)^{10} \approx 1 - 10p + 45p^2$ の近似を用いています。

近似計算

二項定理の式の第3項（$p$の2次）までを計算した。

$$\begin{aligned} (1-p)^{10} &= \binom{10}{0}(-p)^{0} + \binom{10}{1}(-p)^{1} + \binom{10}{2}(-p)^{2} + ... \\ &\approx 1 - 10p + 45p^2 \end{aligned}$$

連番 vs バラ ⇒ バラの勝利

両者を比較すると、それぞれ第1項 $10(w_1 + 2w_2)p$ は共通ですので、第2項の大小によってどちらが得かを検討します。
pが充分小さいので、

$$\begin{aligned} &(連番の場合の期待値) - (バラの場合の期待値) \\ &= 45(w_1 + 2w_2)p^2 - 2w_2p \\ &= (45(w_1 + 2w_2)p - 2w_2)p \lt 0 \end{aligned}$$

よって、1セットのみを購入する場合はバラのほうが当せん金の期待値が大きくなります。

前提の $(p, w_1, w_2)$ の値を代入すると、期待値は以下の通り。（1等、前後賞のみ）

• 連番の場合: 485.0000円
• バラの場合: 499.9999円

$n$セット購入の場合

連番で購入したとき

連番を$n$セット購入する場合、$10n$枚をすべて連番で購入する方法と、10枚連番を飛び地で購入する方法が考えられますが、より期待値が高くなる前者の方法を採用します。
1セットの場合と同様に購入範囲の境界での前後賞を考慮すると、当せん金の期待値は

$$10n(w_1 + 2w_2)p - 2w_2p$$

と表せます。

なお、後者の10枚連番を飛び地で購入する方法での当せん金の期待値は

$$10n(w_1 + 2w_2)p - 2nw_2p$$

となり、明らかに前者より小さくなります。

バラで購入したとき

バラで購入した場合も、1セットの場合と同様の考察により当せん金の期待値は

$$(w_1 + 2w_2)(1-(1-p)^{10n}) \approx 10n(w_1 + 2w_2)p - 5n(10n-1)(w_1 + 2w_2)p^2$$

となります。
ここで、$p \ll 1$ のとき $(1-p)^{10n} \approx 1 - 10np + 5n(10n-1)p^2$ の近似を用いています。

近似計算

二項定理の式の第3項（$p$の2次）までを計算した。

$$\begin{aligned} (1-p)^{10n} &= \binom{10n}{0}(-p)^{0} + \binom{10n}{1}(-p)^{1} + \binom{10n}{2}(-p)^{2} + ... \\ &\approx 1 - 10np + \frac{10n(10n-1)}{2} p^2 \\ &= 1 - 10np + 5n(10n-1) p^2 \end{aligned}$$

連番 vs バラ ⇒ 346セット以下であればバラの勝利

ここでも1セットの場合と同様に、第2項の大小によってどちらが得かを検討します。

$$\begin{aligned} &(連番の場合の期待値) - (バラの場合の期待値) \\ &= 5n(10n-1)(w_1 + 2w_2)p^2 - 2w_2p \end{aligned}$$

ちょっとよくわからないので、前提の $(p, w_1, w_2)$ の値を代入してシミュレーションを行いました。

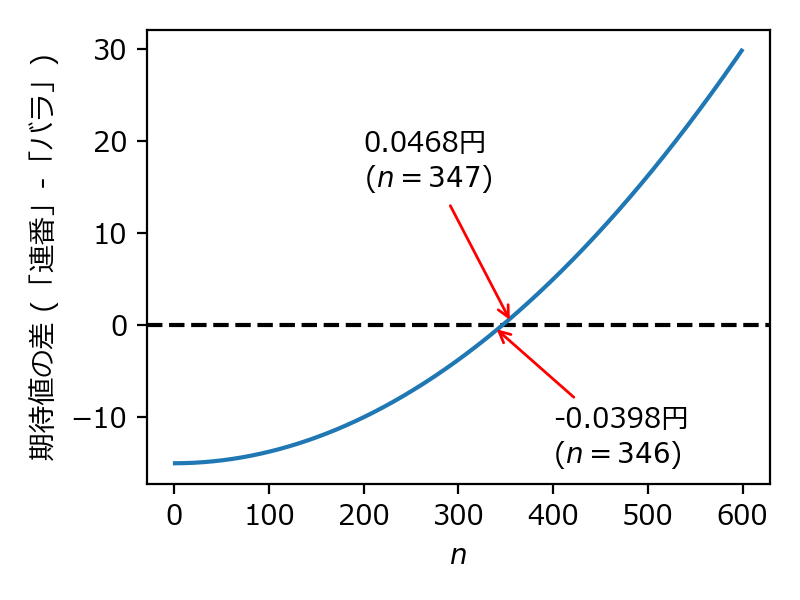
シミュレーション結果

結果、$n=346$ まではバラの当せん金の期待値がより大きく、$n=347$ からは連番の当せん金の期待値がより大きくなります。

347セット購入するときの費用は約104万円です。
対して、当せん金の期待値は17.3万円となります。（1等、前後賞のみ）

結果

年末ジャンボ宝くじを買うときはバラで購入しましょう。
※ただし、同時に347セット以上購入する場合は連番にしましょう。

Limitations

1等、前後賞以外については考察していません。
連番とバラで差が出るのは前後賞の扱いのみと思われるので、差の検証においては支障ないはずですが、計算した期待値は実際よりも低く見積もられています。

その他、計算ミス等がありましたらコメントしていただけると嬉しいです。
最後までお付き合いいただきありがとうございました。