広義積分とは
\begin{align*}
\text{定義 :} \quad & \int_{-\infty}^b f(x) dx=\lim_{a \to -\infty} \int_a^b f(x) dx \\[2em]
& \int_a^{\infty} f(x) dx=\lim_{b \to \infty} \int_a^b f(x) dx \\[2em]
& \int_{-\infty}^{\infty} f(x) dx=\lim_{a \to \infty} \int_{-a}^a f(x) dx
\end{align*}
つまり定積分 \displaystyle \int_a^b f(x) dx の a か b を \infty か -\infty に置き換えたもの。
解法
極限の式に直して解く。
あとは普通に定積分をして、最後に \lim を解けばいいだけ。
例題
例題1
まず極限の式に直す。
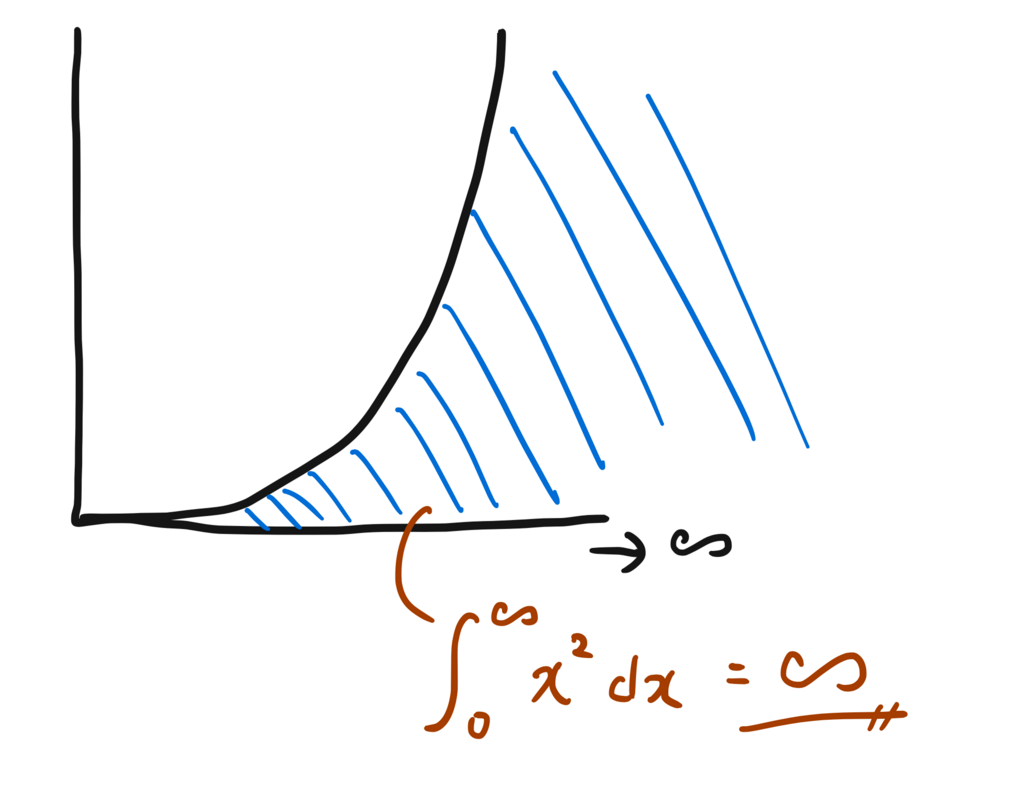
\int_0^{\infty}x^2 dx=\lim_{a \to \infty} \int_0^a x^2 dx
定積分をする。
\begin{align*}
\lim_{a \to \infty} \int_0^a x^2 dx &= \lim_{a \to \infty} \left[\frac{x^3}{3}\right]^a_0 \\[2em]
&= \lim_{a \to \infty} (\frac{a^3}{3}-\frac{0^3}{3}) \\[2em]
&= \lim_{a \to \infty} \frac{a^3}{3} \\[2em]
&= \infty
\end{align*}
まあグラフで見れば一目瞭然だが。
例題2
\int_1^{\infty}\frac{1}{x^2} dx
まず極限の式に直す。
\int_1^{\infty}\frac{1}{x^2} dx=\lim_{a \to \infty} \int_1^{a}\frac{1}{x^2} dx
定積分をする。
\begin{align*}
\lim_{a \to \infty} \int_1^{a}\frac{1}{x^2} dx &= \lim_{a \to \infty} \left[-\frac{1}{x}\right]^a_1 \\[2em]
&= \lim_{a \to \infty} \left[(-\frac{1}{a})-(-\frac{1}{1})\right] \\[2em]
&= \lim_{a \to \infty} (1-\frac{1}{a}) \\[2em]
&= 1
\end{align*}





Discussion