誤差関数とは

前提知識

• 正規分布

誤差関数 (Error Function) の定義

誤差関数はガウス直々の定義らしく、以下のように定義される。

$$\text{定義 :} \quad \text{誤差関数} ~ erf(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt$$

$x \to \infty$ のとき誤差関数は $1$ となる。

$$erf(\infty)=\frac{2}{\sqrt{\pi}}\int_0^\infty e^{-t^2}dt=1$$

なので、このように 相補誤差関数 (Complementary Error Function) $erfc(x)$ を定義できる。

$$\text{定義 :} \quad \text{相補誤差関数} ~ erfc(x)=1-erf(x)=\frac{2}{\sqrt{\pi}}\int_x^\infty e^{-t^2}dt$$

この $erf(x)$ と $erfc(x)$ のどちらも誤差関数と呼ぶことがあるが、ふつう誤差関数といえば $erf(x)$ を指す。また $erfc$ は 余誤差関数 と呼ぶこともある。

誤差関数の意味

それではこの誤差関数はなにを表す関数なのか？

名前の通り 誤差がある範囲に収まる確率 を表す。そういう意味で、正規分布つまり誤差分布とおなじことを違うかたちで書いているともいえる。

正規分布との関係

誤差関数は、正規分布を違う形で表したものともいえる。

誤差の収まる範囲

あらゆる誤差は正規分布に従うとされているので、誤差が $\pm a\sigma$ に収まる確率は、標準正規分布のPDF $pdf_{SDN}$ を $-a$ から $a$ まで積分すれば求まる。（誤差なので、いうまでもなく平均は０）

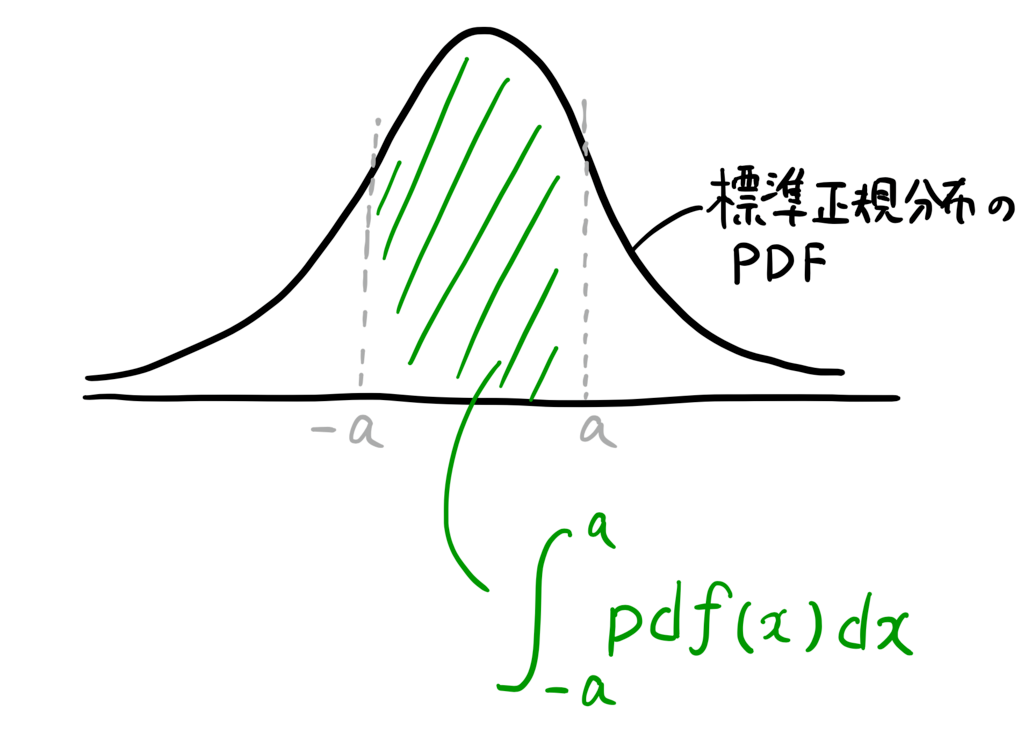
すると、これを誤差関数で表せる。

$$\begin{align*} \int_{-a}^{a}pdf_{SND}(x)dx \quad = \quad \frac{2}{\sqrt{\pi}}\int_0^\frac{a}{\sqrt{2}} e^{-t^2}dt \quad = \quad erf(\frac{a}{\sqrt{2}}) \\[2em] {\small\text{ただし}} \quad pdf_{SND}(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \quad {\small\text{(標準正規分布のPDF)}} \end{align*}$$

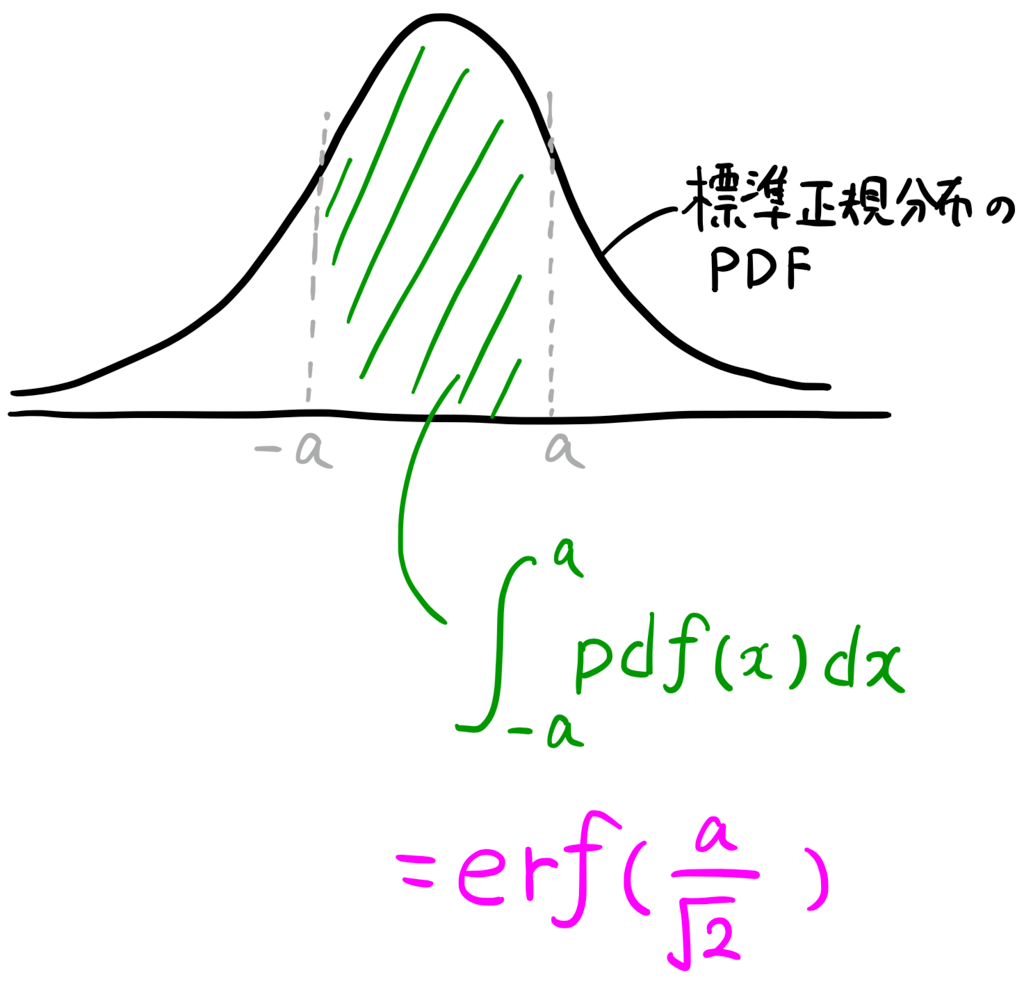
つまり $erf(x)$ とは 誤差が $\pm \sqrt{2}x\sigma$ の範囲に収まる確率そのもの といえる。

$$erf(x) = P\left[\ -\sqrt{2}x\sigma \leq \text{誤差} \leq\sqrt{2}x\sigma\ \right]$$

導出

誤差が $\pm a\sigma$ に収まる確率（＝標準正規分布のPDFを $-a$ から $a$ まで積分）を誤差関数で表したいから、

$$\int_{-a}^{a}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx=\int_0^{f(a)}\frac{2}{\sqrt{\pi}}e^{-x^2}dx \quad {\small (\text{右辺は}erf(f(a)))}$$

となる $f(a)$ を求める。（ $\displaystyle erf(\infty)=1,\ \int_{-\infty}^\infty pdf(x)dx=1$ なので、解は存在する）

標準正規分布は $0$ を中心に左右対称なので $\displaystyle \frac{1}{2}\int_{-a}^a pdf_{SND}(x)dx=\int_{0}^a pdf_{SND}(x)dx$ だから、両辺を $\displaystyle \times \frac{1}{2}$ して

$$\frac{1}{\sqrt{2\pi}}\int_{0}^{a}e^{-\frac{x^2}{2}}dx=\frac{1}{\sqrt{\pi}}\int_0^{f(a)}e^{-x^2}dx$$

両辺を微分 (定積分の微分公式より)

$$\begin{align*} \text{左辺 :} \quad & \frac{d}{da}\,\bigl(\ \frac{1}{\sqrt{2\pi}}\int_{0}^{a}e^{-\frac{x^2}{2}}dx\ \bigr)=\frac{1}{\sqrt{2\pi}}(e^{-\frac{a^2}{2}}\times 1 -e^{-\frac{0^2}{2}}\times 0)= \frac{1}{\sqrt{2\pi}}e^{-\frac{a^2}{2}} \\[2em] \text{左辺 :} \quad & \frac{d}{da}\,\bigl(\ \frac{1}{\sqrt{\pi}}\int_0^{f(a)}e^{-x^2}dx\ \bigr)=\frac{1}{\sqrt{\pi}}(e^{-f(a)^2}\times f'(a) -e^{-0^2}\times 0)= \frac{f'(a)}{\sqrt{\pi}}e^{-f(a)^2} \end{align*}$$

左辺 $=$ 右辺とすると

$$\begin{align*} \frac{1}{\sqrt{2\pi}}e^{-\frac{a^2}{2}} &= \frac{f'(a)}{\sqrt{\pi}}e^{-f(a)^2} \\[2em] \frac{1}{\sqrt{2}}\, e^{-\frac{a^2}{2}} &= f'(a) \, e^{-f(a)^2} \end{align*}$$

つまり

$$\begin{cases} \frac{1}{\sqrt{2}}=f'(a) \\[1em] -\frac{a^2}{2}=-f(a)^2 \end{cases}$$

なので、これを満たす $f(a)$ は

$$f(a)=\frac{a}{\sqrt{2}}$$

と求まる。

標準正規分布のCDFを誤差関数で表す

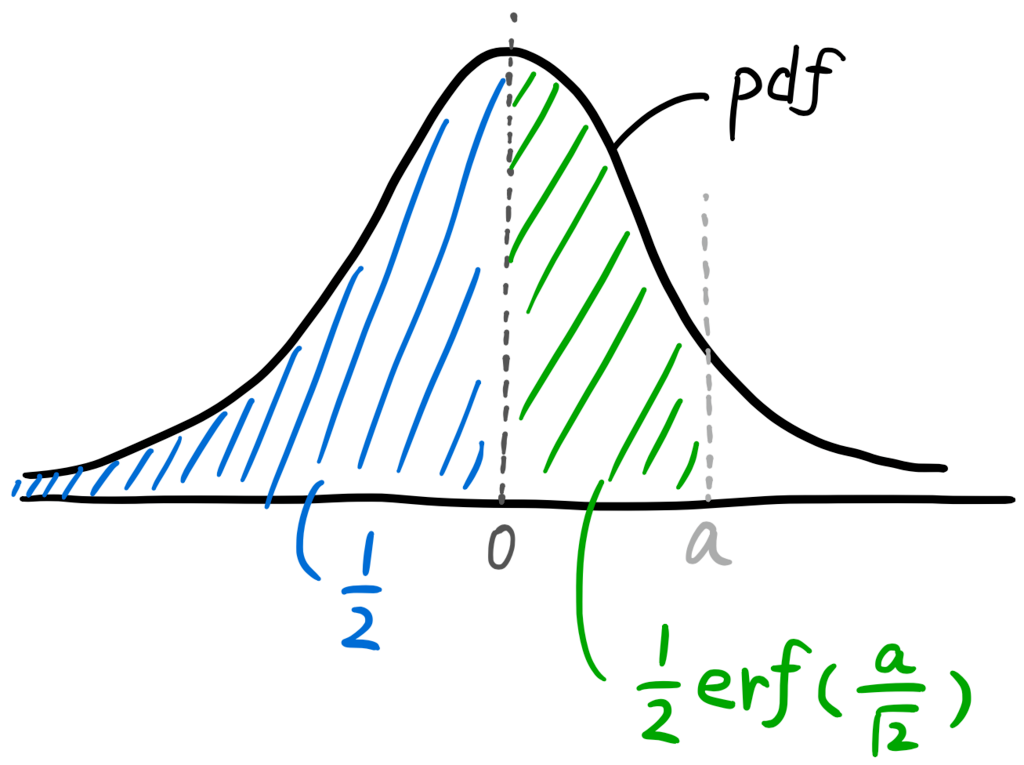
上を踏まえると、標準正規分布のCDF（累積分布関数） $CDF_{SND}$ を誤差関数で表せる。

$$CDF_{SND}(a)=\frac{1}{2}\ +\ \frac{1}{2}\, erf(\frac{a}{\sqrt{2}})$$

導出

上のグラフを見れば一目瞭然だが、一応。

$$\begin{align*} CDF_{SND}(a) &= \int_{-\infty}^a pdf_{SND}(x)dx \\[2em] &= \int_{-\infty}^0 pdf_{SND}(x)dx + \int_0^a pdf_{SND}(x)dx \end{align*}$$

$\displaystyle \int_{-\infty}^0 pdf_{SND}(x)dx=\frac{1}{2},\ \ \int_0^a pdf_{SND}(x)dx=\frac{1}{2}\int_{-a}^a pdf_{SND}(x)dx$ なので

$$CDF_{SND}(a)=\frac{1}{2}\ +\ \frac{1}{2}\int_{-a}^a pdf_{SND}(x)dx$$

ここで、上で示したように $\displaystyle \int_{-a}^{a}pdf_{SND}(x)dx=erf(\frac{a}{\sqrt{2}})$ なので

$$CDF_{SND}(a)=\frac{1}{2}\ +\ \frac{1}{2}\, erf(\frac{a}{\sqrt{2}})$$