『関数型プログラミングの基礎』を読んだ
さらに関数型プログラミングへの理解を深めるために本書を手に取った。
JavaScriptを使って関数型プログラミングを説明してくれるのでとても理解がはかどる。また、参照透過性を金貨にたとえたり、関数を自動販売機にたとえたりといった、身近な例とユーモアを交えて関数型プログラミングを説明してくれるところが面白い。関数型プログラミングが数学的推論を可能とする例の説明においては、高校数学で使われる"関数"とどこが同じなのかを丁寧に説明してくれる。こういったわかりやすい身近な事例から、本質的な理解をじっくりと醸成させてくれる大学の教科書のようないい本だった。
ただ難易度としては学術的な観点でいう基礎という印象がある。
中盤以降の内容は、配列をイミュータブルデータと純粋関数のみで実装してみるなど、関数型言語の内部実装を実際にJavaScriptでやるとどんな実装になるか、という観点での説明となっていく。
またストリームを自前で実装してみたり、再帰を多用したりもする。代数的データ構造(ADTs)をJavaScriptで自前で実装するあたりは、そもそもADTs自体を知っていないと、かなり難易度が高い気がした。代入を使用しない再帰処理での実装などは、スタックの理解が前提にないとなかなか辛い。IOやMAYBEのモナドの説明の箇所は、そもそもIOやMAYBEを使ったことがないと内部実装を読み解けてもその効用まで理解できない可能性がある。本書は全体的に、そもそもの関数型プログラミングの事前知識や実践がないと途中でウッとなってしまうかもしれないと思った。ただ内容は難しいが、『なっとく関数型プログラミング』や『なっとくアルゴリズム』などをすでに読んでいると、わりとすんなり頭に入ってくる気はする。むしろ個人的には、バキバキに関数型プログラミングを実践している人以外は、この2つの書籍をやってから本書に取り組むことをおすすめする。
一方で、プログラミング自体の理解として最初に持っておくべき心得なども初心者向けに記載されているので、想定としては関数型プログラミングに関心のある理系(CS?)学部の学生が最初に取り組む本として書かれている印象だった。Amazonのコメントにもあったが、プログラミングの即効性というよりは、しっかりと学問的に基礎から関数型プログラミングに取り組みたい人に適する本かと思う。
読み進めるにあたっては、以前の実装(listなど)を頻繁に参照する必要があるため、コードを実際に書きつつ理解しながら読み進めた方がよさそうだなと思った。
関数型プログラミングをさらに深堀したいという私としてはとても有用な本だった。
関数型プログラミングの利点のまとめ
- 関数型プログラミングの利点
- コードのモジュール性が高まる
- 再利用性の高いコードの利点
- コードの量や依存が減り、バグを予防できる
- 結果的にバグの発生を抑えることにつながる
- コードをメンテナンスしやすくする
- 同じ部品を再利用していれば、修正は1箇所で済む
- 複雑性をよく制御できる
- 再利用される部品は、人間が普段使う概念とよく対応する
- プログラム全体の見通しが良くなり、複雑性に対抗する強力な手段
- コードの量や依存が減り、バグを予防できる
- 再利用性の高いコードの利点
- コードのテストを容易にする
- 参照透過性によって依存関係が明確になり、また副作用を分離することで純粋関数箇所をテスト可能にすることができる
- プロパティベーステストによりランダム値を使用して検証できるようになる
- コードの正しさを証明できる
- 数学的に証明が可能になる
- コードのモジュール性が高まる
はじめに
- 法学からプログラミングに入り、最後に行き着いたのが関数型プログラミング
- JavaScriptはファーストクラスオブジェクトとしての関数を備えている
関数型プログラミングの基礎
-
計算とは
- 命令型と関数型の計算モデルが違う
- 命令型モデルはチューリング機械に原型がある
- 関数型モデルはラムダ計算という数学の理論に源流がある
- 「計算」のモデル
- 命令型プログラミングと関数型プログラミングは、計算モデルが違う
- 人間と違って機械は計算について何も知らない
- 計算モデルが必要
- 命令型モデル: 計算とは命令を実行すること
- C言語など
- 関数型モデル: 計算とは関数を呼び出して値を得ること
- HaskellやLispなど
- 論理型モデル: 計算とは証明を得ること
- Prologなど
- 命令型モデル
- 命令を実行することが計算と捉える
- 命令とは、計算機の状態を変更する処理のこと
- 計算機の記憶装置や表示装置の中身が変化して、最後の状態を結果と考える
- 逆ポーランド電卓
- 1と2を押してから、+を押すと、3が返る
- スタックに値を入れていくと、スタックの状態が変化していく
- チューリング機械
- 1930年代にアラン・チューリングが考案した
- 長いレールの上を走る電車のようなもの
- マス目に区切られた無限のテープのレールの上を、左右に移動できるテーブルのヘッドで、0と1の記号を読み込んだり書き込んだりする
- できることは、読み込み、書き込み、前か後ろに1つ移動する、テーブルに格納されている状態を変更することのみ
- 状態が最終状態に到達するまで反復して実行し続ける
-
チューリング機械
var machine = (program, tape, initState, endState) => { /* ヘッドの位置 */ var position = 0; /* 機械の状態 */ var state = initState; /* 実行する命令 */ var currentInstruction = undefined; /* 以下のwhileループにて、 現在の状態が最終状態に到達するまで命令を繰り返す */ while (state != endState) { var cell = tape[String(position)]; if (cell) { currentInstruction = program[state][cell]; } else { currentInstruction = program[state].B; } if (!currentInstruction) { return false; } else { /* テープに印字する */ tape[String(position)] = currentInstruction.write; /* ヘッドを動かす */ position += currentInstruction.move; /* 次の状態に移る */ state = currentInstruction.next; } } return tape; };
- コンピュータのストレージは0と1の並びを格納しているにすぎず、計算機が出力した0と1の並びを、適切な場所に色彩として高解像のモニターに表示しているだけ
- チューリング機械におけるテープとしてモデル化できる
- チューリング機械は計算機の原型である
- 命令型はある観点で見ると直感的
- 命令型モデルのわかりにくさ
- 冗長さ
- チューリング機械の状態が把握しづらく、しかもその状態を常に意識してプログラムを書かないといけない
- チューリング機械の状態とは、ある時点でのテープの内容とヘッドの位置である
- 関数型モデル
- チューリング機械が発表されたほぼ同時期に、アメリカの数学者アロンゾ・チャーチがラムダ計算を定義した
- 計算とは、関数を適用して値を得ること
- ラムダ式:
f(x)=2x+1 \lambda x. 2x + 1 - これを関数抽象(function abstraction)と呼ぶこともある
- JavaScript:
(x) => 2 * x + 1
- チューリング機械ではテープやヘッドで計算していたが、ラムダ計算ではどうやって関数を計算するのか
- 幾何学的な方法: グラフを描いて調べる
- 代数的な方法:
f(x)=2*x+1 - この方法で計算される
-
{ return x + 1; }は{ return 1 + 1; }へと変換される - これを置換ルール(置換モデル)と呼ぶ
- 置換ルールに従って式が簡単になることを簡約と呼ぶ
- 代入を使うと置き換えルールによる簡約ができなくなる
-
whileを使ったループによる変数の更新など
- 関数から関数を返したり、関数の引数として関数を渡したりすることで、豊かな表現力が得られる
-
かけ算
var times = (count, func, arg, memo) => { if (count > 1) { /* times関数を再帰的に呼び出す */ return times(count - 1, func, arg, func(arg, memo)); } else { return func(memo, arg); } }; var multiply = (n, m) => { /* 2番目の引数にadd関数を渡している */ return times(m, add, n, 0); }; - 計算の中間結果を蓄えておく変数
memoは、蓄積変数(accumulator)と呼ばれる
-
- 命令型モデルにもとづいたアセンブラやC言語の方が隆盛を誇った背景
- ハードウェアの構造に近い命令型モデルの方が実現しやすく、関数型モデルではメモリやコンパイルの効率的な管理が難しかったため
- CPU処理能力の向上やメモリの巨大化で、計算リソースが豊かになるにつれて解決されてきた
- 関数型モデルを使うメリット
- 置換ルールという計算の仕組みのシンプルさ
- 処理自体を部品化できることで高いモジュール性を持つ
- チューリング機械が発表されたほぼ同時期に、アメリカの数学者アロンゾ・チャーチがラムダ計算を定義した
- 命令型と関数型の計算モデルが違う
なぜ関数型プログラミングが重要か
- 関数プログラミングの特徴
- 関数を通常の値のように扱えること
- 参照透過性という考え方があること
- 参照透過性を破壊する代入や副作用の仕組みがあること
- FPの特徴を活かしてできること
- モジュール性を高めて複雑な処理を簡潔に記述できる
- 複雑な状態管理から解放されてテストが容易になる
- コードの正しさを数学的に証明できる
- (バグを減らすことができる)
- 関数型モデルでの中心的な要素はラムダ式
- 命令型モデルでは命令が主体
- 数学的な意味での関数とは
- 「ある値に対して、ただ1つの値が対応するような関係」
- 例: 自動販売機: 小銭を入れてボタンを押すと、コーラが1本出てくる
- 「入力が同じであれば、いつどこで呼び出されても返ってくる値は同じになる」という性質
- 例: コーラのボタンを押せば毎回コーラが出てくる。あるとき突然カルピスが出てくることはない
- 「ある値に対して、ただ1つの値が対応するような関係」
- プログラミング言語における関数は、計算手順をアルゴリズムとして定義する必要がある
- 関数型プログラミングが使える条件
- 関数がファーストクラスオブジェクトとして使用可能なこと
- 可能となる操作
- 関数を変数にバインドする
- 関数の本質はその振る舞いにある
- 無名関数であるラムダ式を変数にバインドすることで、名前をつけることができる
- 関数をデータ構造に埋め込む
- 似た機能を持つ関数を1箇所にまとめることができる(BoF)
- 関数適用の際に関数を引数として渡す
- 関数渡しによって、高階関数を利用できる
-
forEachは関数を受け取ってそれぞれに実行する
- 関数から関数を返す
- 関数から関数を返すことで、カリー化が可能になる
- 目的に応じた具体的な関数を作り出すことができる
-
var adder = (n) => { return (m) => { return n + m; }; };
- 関数から関数を返すことで、カリー化が可能になる
- 関数を変数にバインドする
- 可能となる操作
- 参照透過性を確保できること
- 「プログラムの構成要素が同じもの同士は等しい」という性質
-
A === A: 「今年の元旦に私が食べた全てのお餅 === 今年の元旦に私が食べた全てのお餅」 - 左右のAが指し示すものは、等しくなければならない
- プログラミング言語によって、必ずしも参照透過性が保証されているとは限らない
- 置換ルールの読み替え
- 関数呼び出しの結果は、その関数の引数のみに依存する
- ある関数のへの引数が同じであれば、その関数は必ず同じ値を返さなければならない
- 同じ引数で何度実行されても同じ値を返す
-
- 同じコンテキスト(文脈)において、そっくり同じに表現された対象は、同じものと判断される
- 基数というコンテキストが一緒であれば、10は10と同一
- 例: 手元の100円玉は、どの100円玉でも同じ100円という価値の硬貨であると考えられる
- 参照透過性を破壊するもの
- 可変なデータ
-
pushは破壊的メソッド - array変数名は同じでも中身が変更されている
-
- 代入は参照透過性を破壊する
- コードが暗黙の状態(コンテキスト)を保持しているから
- コンテキストとは
- 「8月は1年の中で最も暑い季節です」
- 一見正しいように見える
- 場所というコンテキスト(暗黙の状態)が潜んでいる
- 南半球のオーストラリアでは8月は冬で、むしろ一番寒い季節となる
- (アンコンシャスバイアスにも近い)
-
whileなどの反復文で必須のため、代入という仕組みを多くの言語が準備している
- 可変なデータ
- 副作用とIO
- もともと参照透過でない関数がある
-
Date.nowメソッドなど - 毎回異なる値を返す
-
- IO: プログラミング言語の処理系へのデータの入力や出力
- 入出力とは
- 画面の表示やファイルへの書き込みなどの出力
- キーボードによる文字入力やファイルからの読み出しなどの入力
- これらは副作用と呼ばれる
- 副作用を持つ関数には、参照透過性がない
- 代入も可変なデータ構造も使用していないが参照透過性が失われる
- IOが処理系にとって隠蔽されたコンテキストとして振る舞うため
- 変数は処理系の直接的な支配下にある一方、画面やストレージは処理系の周辺に位置するから
- 入出力とは
- 例: 金貨の金含有量が減ると、参照透過性を喪失することになる
- もともと参照透過でない関数がある
- 「プログラムの構成要素が同じもの同士は等しい」という性質
- 関数がファーストクラスオブジェクトとして使用可能なこと
- 参照透過性を保証する
- 可変なデータや、代入、副作用によって参照透過性は破壊される
- 保証する方法
- 可変なデータを不変なデータ構造として構築する
-
不変なデータ構造としてのオブジェクト型の実装
var empty = (_) => { return null; }; var get = (key, obj) => { return obj(key); }; var set = (key, value, obj) => { return (key2) => { if (key === key2) { return value; } else { return get(key2, obj); } }; };
-
- 代入の排除で、変数の参照透過性を保証する
- 反復処理をどう実現する?
-
代入を使わずに再帰で反復処理を実現する
/* 反復文を用いた足し算の定義 */ var add = (x, y) => { var times = 0; var result = x; while (times < y) { result = result + 1; times = times + 1; } return result; }; /* 関数型プログラミングによる足し算の定義 */ var add = (x, y) => { if (y < 1) { return x; } else { return add(x + 1, y - 1); } };
- 副作用の分離で、関数の参照透過性を保証する
- 基本戦略は、副作用を持つ部分と副作用を持たない部分をきちんと分離すること
- UIや、DBへのIO
- IOモナドを使って入出力をカプセル化するなど
-
コンテキストを引数として渡して副作用を分離する
/* 副作用が分離されていないコード */ var age = (birthYear) => { var today = new Date(); var thisYear = today.getFullYear(); return (thisYear = birthYear); }; /* 現在の時刻というコンテキストを引数として渡した、副作用が分離されたコード */ var age = (birthYear, thisYear) => { return thisYear - birthYear; };
- 基本戦略は、副作用を持つ部分と副作用を持たない部分をきちんと分離すること
- 可変なデータを不変なデータ構造として構築する
- 関数型プログラミングの利点
- 関数型プログラミングでは代入も可変なデータも許されない
- ストイックすぎる?
- 中世の修行僧ではなく、オリンピックアスリートのようなもの
- より高く飛びより速く走るために練習や食事を厳しくコントロールする
- 強靭でしなやかな肉体を手にいれる
- 大きな問題を小さな問題に分割して解くこと
- 「困難を分割せよ」 ルネ・デカルト『方法論序説』
- 工学の分野ではモジュール化の手法となった
- 利点
- コードのモジュール性が高まる
- 全体を小さなブロックに分割するという戦略
- レゴブロックのようなもの
- データや変数を関数で繋ぎ合わせる
- 手順(分割統治に近い)
- 大きな問題を小さな問題に分割する
- 小さな部品で小さな問題を解く
- 小さな問題を解く小さな部品を組み合わせて、大きな問題を解く
- 部品の独立性
- 参照透過な関数の結果は引数のみに依存する
- それ以外のコードの影響を受けない
- 隠れたコンテキストによって値が変更される恐れがない
- だから部品の独立性が高まる
- 参照透過な関数の結果は引数のみに依存する
- 部品の汎用性
- 汎用性とは、どこでも使うことができるという性質
- レゴブロック
- 同じブロックがさまざまなところで他のブロックと接続できる
- これと反対なのがジグソーパズルのピース
- 単純で統一的なインターフェースを持つことが重要
- レゴブロックの表面の凹凸の設計
- 関数型プログラミングにおいての関数の引数
- カリー化によって組み合わせやすくなる
- 関数渡しでも汎用性を高められる
-
reduceという汎用的な部品によってさまざまな関数を作り出すことができる -
reduceによるsum関数の定義
var sum = (array) => { return array.reduce((accumulator, item) => { return accumulator + item; }, 0); }; - mapで配列をまるごと別の配列に変換することもできる
-
- 再利用性の高いコードの利点
- バグを予防できる
- 結果的にバグの発生を抑えることにつながる
- コードをメンテナンスしやすくする
- 同じ部品を再利用していれば、修正は1箇所で済む
- 複雑性をよく制御できる
- 再利用される部品は、人間が普段使う概念とよく対応する
- プログラム全体の見通しが良くなり、複雑性に対抗する強力な手段となる
- バグを予防できる
- 汎用性とは、どこでも使うことができるという性質
- 部品を組み立て合成できる
- カリー化関数の部分適用で新しい関数を容易に定義できる
-
カリー化によってlength関数を作成する
/* constant関数の定義 */ var constant = (any) => { return (_) => { return any; }; }; var alwaysOne = constant(1); /* map(alwaysOne)で配列の全要素を1に変換する */ expect(map(alwaysOne)([1, 2, 3])).to.eql([1, 1, 1]); /* sum関数に適用すると、length関数が完成する */ var length = (array) => { return sum(map(alwaysOne)(array)); }; - 関数合成による処理の合成
-
データを関数で次々と変換して最終的な結果を得る
- 「英語のY」を上下反転すると「ギリシャ語のラムダ」になり、さらに左右反転すると「漢字のヒト」に変換される
- 「ギリシャ語のラムダ」が不要ならパイプラインを繋げれてしまえばいい
-
データが関数のパイプラインを通って次々と加工されていき、最終的に目的の製品が出てくる工場のようなもの
-
処理を繋ぎあわせる操作を関数の合成と呼ぶ
-
compose関数による関数合成
var compose = (f, g) => { return (arg) => { return f(g(arg)); }; }; /* compose関数による関数合成(ポイントフリースタイル) */ var length = compose(sum, map(alwaysOne)); /* compose関数による関数合成(引数を明示したスタイル) */ var length = (array) => { return compose(sum, map(alwaysOne))(array); }; - 「配列の要素をすべて1に変換し、それらを合計したものが配列の長さである」という手順を簡潔に定義できる
-
-
- 関数による遅延評価
- 遅延評価によって関数のモジュール性をさらに高めることができる
- 遅延評価とは、コードの一部の計算が後回しにされる評価の方法
-
無名関数の評価は先送りされる
/* 正格評価の例 */ length([1, 1 + 1]); /* 遅延評価の例 */ length([ 1, (_) => { return 1 + 1; }, ]); -
ストリームの例
/* ストリームの例 */ // 後尾を取り出すにはaStream[1]()とする必要がある var aStream = [ 1, (_) => { return 2; }, ]; /* 永遠に続く無限の自然数列ストリーム */ var enumFrom = (n) => { return [ n, (_) => { // ストリームを返す return enumFrom(succ(n)); }, ]; }; /* 無限の偶数列を作る */ var evenFrom = (n) => { return [ n, (_) => { return evenFrom(n + 2); }, ]; }; var evenStream = evenFrom(2); /* 規則的なストリームを作る */ var iterate = (init) => { return (step) => { return [ init, (_) => { return iterate(step(init))(step); }, ]; }; };
- 遅延評価によって関数のモジュール性をさらに高めることができる
- 遅延評価では、データを処理する側は対象となるデータの長さを気にする必要がない
- データを生成するモジュールとデータを処理するモジュールの独立性が高まる
- 全体を小さなブロックに分割するという戦略
- コードのテストを容易にする
- 参照透過性があるコードは依存関係が明確
- テストを何度繰り返しても結果は不変
- 副作用を分離すれば、純粋関数はテストで挙動を確認できるようになる
- 引数としてスタブ値を与えれば純粋関数箇所はテストできる
- 参照透過性があるコードは依存関係が明確
- コードの正しさを証明できる
- コードに数学的な性質という恩恵をもたらす
- 推論が可能になるということ
- 等号
===によって2つの式が等しいと主張できること - どんなxに対しても
x === xでなければならない - 参照透過性はこれを保証している
- 等号
- あらかじめ定義した式Aをもとにして式Bが導けたとき、式Bは推論による新しい知識ということになる
- 推論が可能になるということ
- 証明で正しさを検証できる
- 命題:
succ(0) + succ(x) === succ(succ(x)) - xを1とおく:
succ(0) + succ(1) === succ(succ(1))1 + 2 === 3
- 証明に利用する等式:
succ(N) === N + 1 - 等式推論によって命題を証明できる
- どちらも最終的に
1 + (x + 1)に変換される
- どちらも最終的に
- 命題:
- プロパティテスト(property-based testing)で正しさを証明できる
- 大量のテストケースを自動的に生成して、それらのテストケースについてコードが一定の性質を保っているかどうか検証する
- ScalaCheckなどのライブラリも使用できる
- コードに数学的な性質という恩恵をもたらす
- コードのモジュール性が高まる
- 関数型プログラミングでは代入も可変なデータも許されない
JavaScriptによる関数型プログラミングの実践
- プログラミングの心得
- DRY原則
- DRYでのリファクタリングは再帰の処理部分を関数化する
-
DRYなtimes関数
var times = (count, arg, memo, fun) => { if (count > 1) { return times(count - 1, arg, fun(arg, memo), fun); } else { return fun(arg, memo); } }; - DRYなコードは推敲された文章と似ている
-
- DRYでのリファクタリングは再帰の処理部分を関数化する
- 抽象化への指向
- 抽象化は、人間が苦手とする細部の複雑性を隠蔽してくれる
- 関数型プログラミングが得意とするのは、振る舞いの抽象化
-
reduceによるsum関数の定義
var sum = (array) => { return array.reduce((x, y) => { return x + y; }); }; - 抽象化されていない古い機織り機を使いこなすのは、村で一番長生きしたお婆さんだけかもしれないが、一方現代の機織り機は、仕組みの詳細がわからなくても誰でも簡単に操作できる
- 人間の苦手とする複雑性を、現代の機織り機が代替し、隠蔽してくれているから
-
- セマンティクスを意識する
- シンタックスは、単なるアルファベットや記号の列にすぎない構文
- プログラムという目に見えるコード
- その背後にセマンティクスという見えない領域が隠されている
- プログラミング言語の処理系で隠された詳細がセマンティクスと呼ばれる領域
- シンタックスは、単なるアルファベットや記号の列にすぎない構文
- テストに親しむ
- 抽象化されたコードを理解し、DRYなコードにリファクタリングするために、テストを書く
- 単体テスト
-
堅固な城壁が天守閣を幾重にも囲むように、単体テストはバグの混入を防ぎ、ソフトウェアの複雑性に対抗する手段となる
- 十分な単体テストで個々のコードの挙動を確認できていれば、バグの侵入を防ぐことができる
- リファクタリングも十分なテストが準備されていることが前提となる
-
- DRY原則
- データの種類と特徴
- 型は集合によく似た概念
- 10以下の自然数の集合:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9 10} - 型と集合の違う点
- 型にはその型に対して定義された演算が利用できる
- 集合の演算ではどんな要素を持った集合でも計算できる
- 例:
{1, "dog", true}と{0, "dog", false}の積は、{"dog"}である
- 例:
- 型は階層(多層性)を持つ
-
[[1, 2], [2, 1]]が可能 - 素朴な集合論では階層を持たない
- 20世紀の初めに数学者たちは数学の体系を集合論だけで説明しようとしていた。バードランド・ラッセルはその挑戦の過程で集合論のパラドックスを発見する(ラッセルのパラドックス)
- 同時に真でもあり偽でもある命題
- 例: 「私は嘘つきである」
- 自分自身を要素として含まない集合全体のの集合を考えた時にパラドックスが存在する
- 例: > ある町に、その町の全ての男性の中で「自分で髪を切らない人全員の髪を切る床屋」がいるとします。では、床屋は自分の髪を切るのでしょうか? 床屋が自分の髪を切るなら、床屋は「自分で髪を切らない人」の髪を切る」という定義に反します。床屋が自分の髪を切らないなら、床屋は「自分で髪を切らない人」であり、自分で髪を切らない人である自分自身の髪を切るべき、となってしまいます。
- これを回避するために型という仕組みを考案した
-
型定義によって自己言及的な矛盾を回避する(この話"コンテクスト"では、床屋自身の話は含んでないと明言する)
// 全ての男性を表す型 type Man = { name: string; cutsOwnHair: boolean; // 自分の髪を切るかどうか }; // 床屋の行動を定義する型 type Barber = { name: string; cutsHairOf: (man: Man) => void; // 他の男性の髪を切る }; // 床屋が自分自身を含まない集合に対して行動するように制約を設ける const townMen: Man[] = [ { name: 'John', cutsOwnHair: false }, { name: 'Mike', cutsOwnHair: true }, // 床屋自身の定義 { name: 'The Barber', cutsOwnHair: false } ]; const barber: Barber = { name: 'The Barber', cutsHairOf: (man: Man) => { if (!man.cutsOwnHair) { console.log(`${barber.name} cuts ${man.name}'s hair`); } } }; // 床屋が町の他の男性の髪を切る townMen.forEach(man => { if (man.name !== barber.name) { // 自分自身は含まないという制約を明示する barber.cutsHairOf(man); } });
-
- その後、アロンゾ・チャーチによってラムダ計算に型が取り込まれ、型付きラムダ計算という領域に発展する
- もともとは計算を必ず停止させる仕組みとして型を導入した
- 同時に真でもあり偽でもある命題
-
- 集合の演算ではどんな要素を持った集合でも計算できる
- 型にはその型に対して定義された演算が利用できる
- 10以下の自然数の集合:
- 型は集合によく似た概念
- 変数は引数のない関数と考えることもできる
- ただ、関数は適用して初めて結果が計算される
-
引数のない関数
var three = () => { return 3; }; expect(three()).to.eql(3);
-
- 関数はデータ取得のタイミングを遅らせることができるということ
- 呼び出し側がそのタイミングを自由にコントロールできる
- ただ、関数は適用して初めて結果が計算される
- データの本質はデータのそのものではなく、その操作方法にある: 抽象データ型
- 例: PCに動画があるがキーボードとモニター(インタフェース)が壊れてしまった。HDが生きていたとしても、利用手段がないためそのデータは無意味となる。
- データの実装自体を隠蔽して、その操作方法のみ公開するデータ型を、抽象データ型(abstract data type)と呼ぶ
-
リストは配列よりもデータの操作が制限されている
-
抽象データ型としてのリスト
var empty = () => { // 空のリストを作る処理 }; var cons = (value, list) => { // リストの先頭に値を追加する処理 }; var head = (list) => { // リストの先頭を取り出す処理 }; var tail = (list) => { // リストの後尾(先頭以外の全ての並び)を取り出す処理 }; - 4つの関数がある
-
リストの代数的仕様
tail(cons(VALUE, LIST)) === LIST; // ルール[1]: 先頭がVALUEで後尾がLISTで構成されたリストの先頭は、VALUEである tail(empty()) === null; head(cons(VALUE, LIST)) === VALUE; head(empty()) === null;
-
- リストに1、2という要素を順々に格納して、そこから2番目の要素を取り出す
-
具体的なリストの利用法
expect(head(tail(cons(1, cons(2, empty()))))).to.eql(2);
-
-
- 抽象データ型とは、データを操作するためのインタフェースとデータの実装を明確に区別し、インタフェースのみを利用者に公開するという設計手法
- コードの分業化を可能にして、メンテナンスを容易にすることができる
- インタフェースに適合している限り、関数内部の実装が変わっても問題ないから
- データ型を利用する側とは独立して、関数の実装をリファクタリングできる
- 変数は容器のようにデータを包み込んでいるのではない
- 変数はデータを格納しているのではなく、データを指し示している
- 例: 美術館の場所を指し示す、街中の案内板のようなもの
-
var number = 3;は「変数numberに値3をバインドしている」ことを意味する- 変数にバインドされた値は、その変数名で参照できる
- これをバインド変数と呼ぶ
- 一方で、何の値もバインドしていない変数は自由変数と呼ぶ
- JavaScriptでは自由変数にアクセスすると
ReferenceErrorとなる
- バインディングが有効な範囲をスコープと呼ぶ
- 最も有効範囲の広いスコープをグローバルスコープと呼ぶ
- Mathオブジェクトなど
- 有効範囲の限定されたスコープはローカルスコープと呼ぶ
- JavaScriptでは関数によって作り出される
- 最も有効範囲の広いスコープをグローバルスコープと呼ぶ
- 変数はデータを格納しているのではなく、データを指し示している
- 命令型プログラミングの世界では参照透過性は保証されない
-
[1,2,3] === [1,2,3]はfalseとなる - 可変なデータではアドレスの情報しかないため、アドレスが一致するかどうかという点だけで判断するしかない
- 見た目が同一で合ってもメモリ上の番地が異なれば違うものと判断される
- 代入という操作を実現するには、可変なデータのメモリの仕組みが必要になる
- アドレスを介して変数とデータを対応づけると、変数とデータの直接の対応が失われてしまう
- これを、参照透過性の喪失と呼ぶ
- 参照透過な値は、変数と直接結びついている
- 変数から参照先の値がはっきり見える
-
プログラムをコントロールする仕組み
- プログラムをコントロールする仕組み
- 制御構造と呼ばれる仕組み
- 条件分岐と反復処理の2つがある
- 関数型プログラミングでは再帰呼び出しによって反復処理を実現する
- 条件分岐
- 関数型プログラミングの観点からすると、JavaScriptの
if文は式(expression)ではなく文(statement)なので戻り値がなく、扱いづらい-
console.log関数も典型的な文 - 評価されると値を返すものが式
- HaskellやScalaではifは式として定義されている
- JavaScriptでは
switch文はif文のシンタックス・シュガーである
-
- 代数型データ構造とパターンマッチ
- 複数の選択肢からいずれか1つの型だけを選ぶデータ型を、代数的データ構造と呼ぶ
- 例: ジャンケンのグー、チョキ、パー
- リスト型を代数的データ構造としてJavaScriptで実装してみる
- どのようなリストも
empty()で表現される空のリストか、cons(value, list)で表現される空でないリストのいずれかの形となる -
リスト型を代数的データ構造として実装してみる
/* リストの代数的データ型 */ var empty = () => { return (pattern) => { return pattern.empty(); }; }; var cons = (value, list) => { return (pattern) => { return pattern.cons(value, list); }; }; /* 代数的データ型に対してパターンマッチを実現する関数 */ var match = (data, pattern) => { return data(pattern); }; /* isEmpty関数は、引数alistに渡されたリストが空のリストかどうかを判定する */ var isEmpty = (alist) => { return match(alist, { empty: (_) => { return true; }, cons: (head, tail) => { return false; }, }); }; /* head関数は、引数alistに渡されたリストの先頭の要素を返す */ var head = (alist) => { return match(alist, { empty: (_) => { return null; }, cons: (head, tail) => { return head; }, }); }; /* tail関数は、引数alistに渡されたリストの後尾の要素を返す */ var tail = (alist) => { return match(alist, { empty: (_) => { return null; }, cons: (head, tail) => { return tail; }, }); }; head(cons(1, empty())); -
dataはpatternによって条件分岐を表現していると捉えることができる- (引数として渡した
patternを条件分岐して適用している)- (OOPでいうと、ストラテジーパターンとなる)
- (引数として渡した

-
head(cons(1, empty()))の簡約
head(cons(1,empty())) // ⇒リスト5.14のhead関数を評価する match(cons(1,empty()),{ empty:()=>{ return null; }, cons:(head,tail)=>{ return head; }, }) // ⇒リスト5.13のmatch関数を評価する cons(1,empty())({ empty:()=>{ return null; }, cons:(head,tail)=>{ return head; }, }) // ⇒リスト5.12のcons関数の定義より { empty:()=>{ return null; }, cons:(head,tail)=>{ return head; }, }.cons(1,empty()) // cons関数の定義より (1,empty())=>{ return 1; } // ⇒オブジェクトのconsキーに格納されている関数を実行する { return1; } // ⇒ 1 // 立川察理. 関数型プログラミングの基礎 (Japanese Edition) (pp.197-198). Kindle 版.- (これこそが数学的推論という感じがした)
- どのようなリストも
- 複数の選択肢からいずれか1つの型だけを選ぶデータ型を、代数的データ構造と呼ぶ
- 関数型プログラミングの観点からすると、JavaScriptの
- 再帰による反復処理
- 計算機にとって、反復処理の単純な繰り返しはその威力を存分に発揮できる場面
- 関数型プログラミングでは、関数呼び出しで反復処理を実現する手法が主流
- まず繰り返したい処理を関数として定義する
- その関数の中から自分自身を呼び出すと、同じ処理が繰り返される
- 終了条件を定義する
- 終了条件に近づくように、再帰呼び出しの引数を設計する
- 例: 複利計算
-
再帰によるtoArray関数
var toArray = (alist) => { var toArrayHelper = (alist, accumulator) => { return match(alist, { empty: (_) => { return accumulator; }, cons: (head, tail) => { return toArrayHelper(tail, accumulator.concat(head)); }, }); }; return toArrayHelper(alist, []); }; - 再帰処理の利点
- 再帰処理には代入操作が不要である
-
whileやfor文では、反復回数の保持といった代入操作が必要となる-
forEachでも反復回数は隠蔽されているが、result変数などで代入操作が必要となる
-
- 再帰処理では
accumulator蓄積変数が変化していく- 再帰呼び出しのたびに新しい値として渡されるので、変数を更新しているわけではなく、代入操作ではない
-
- 再帰呼び出しは、再帰的な構造を持つデータの処理に適している
-
cons(1, cons(2, empty()))は再帰的データ構造- あるデータ構造を定義する際にそのデータ構造自身を利用するようなデータ型
-
再帰的データ構造
LIST[T] = empty() | cons(T, LIST[T]);- 再帰的データ構造は同じようなパターンで処理できる
- emptyの場合は再帰の終了条件となる
-
再帰によるlength関数
var length = (list) => { return match(list, { /* emptyの場合は、終了条件となる */ empty: (_) => { return 0; }, cons: (head, tail) => { return 1 + length(tail); }, }); };
-
- 再帰的な構造を持つデータは、その性質の証明に帰納法が利用できる
- 帰納法とは、自然数に関する等式の証明に利用される証明法
- 例: ドミノ倒し
- 基底段階は、1番目のドミノが倒れることを証明すること
- 帰納段階は、もしk番目のドミノが倒れたら、k+1番目のドミノも倒れることを証明すること
- 命題P:
length(append(xs, ys)) === length(xs) + length(ys);- 命題を証明する最も簡単な方法は、左辺と右辺を別々に変形していって最終的に同じ式になると示すこと
- テストを書けばすぐわかるのでは?
- テストは特定のパターンしかテストできない
- テストの数が増えれば命題の確からしさが高まっていくものの、正しいことの論理的な保証にはならない
- 10000個の単体テストが成功しても、10001個目のテストが成功するとは断言できない
- これが単体テストの限界
- 帰納法による証明は、命題が正しいことを論理的に保証している
- これが関数型プログラミングの際立った特徴
- コードが参照透過性を保ち、数学的な意味での関数だけで計算を定義したから可能となること
- テストは特定のパターンしかテストできない
- 再帰処理には代入操作が不要である
- 制御構造と呼ばれる仕組み
関数を利用する
- ラムダ計算には変数と関数しか存在しない
- 関数の基本
- 関数を定義する
- 恒等関数(identity function):
1->1や`"a"->"a"- 入力と同じ値を返す
-
恒等関数
var identity = (any) => { return any; };
- 定数関数: 常に同じ値を返す関数
-
定数関数
var alwaysOne = (x) => { return 1; };
-
- 一部の引数だけを利用し、他の引数を無視する関数
-
left関数
var left = (x, y) => { return x; };
-
- 一見役に立たなそうな単純な関数が、高階関数として関数同士を組み合わせる際に、糊のような役割を果たしてくれる
- 恒等関数(identity function):
- 関数を適用する
-
succ(1)とすると具体的な値が返ってくる - 例: 関数定義はレシピのようなもので、関数適用はさまざまな食材を用いて料理を作る行為に相当する。レシピ自体を食べることはできない。
- 関数自体を評価したときに得られる
[Function]は、クロージャーと呼ばれるもの
-
- 関数の評価戦略
- 関数の引数を直ちに評価する方法を正格評価と呼ぶ
-
add(succ(0), succ(1))では、succ関数から評価した後でadd関数を評価する
-
- 関数適用の際に引数の評価が後回しにされる簡約の方法を、遅延評価と呼ぶ
-
add(succ(0), succ(1))では、add関数から評価する
-
- JSは正格評価が標準だが、Haskellは遅延評価が標準となっている
- 条件文はJSでも遅延評価となる
-
JavaScriptにおいて遅延評価を実装する
// 引数が関数なので、評価されても具体的な値にはならず、 // 関数の本体ブロックのなかで適用して初めて具体的な値になる var lazyMultiply = (funX, funY) => { var x = funX(); if (x === 0) { return 0; } else { return x * funY(); } }; // infiniteLoopは評価されることはなく、無事に計算が終了する expect( lazyMultiply( (_) => { return 0; }, (_) => { return infiniteLoop(); } ) ).to.eql(0); - 引数のない関数で値がラッピングされた構造を、サンクと呼ぶ
- 例:
(_) => { return 0; }
- 例:
- サンクで無限を表現する
-
ストリーム型とリスト型
/* ストリーム型のデータ構造 */ STREAM[T] = empty | cons(T, FUN[(_) => STREAM[T]]); /* リスト型のデータ構造 */ LIST[T] = empty() | cons(T, LIST[T]);- ストリームでは後尾がサンクとして表現されている
- tail関数は、サンクを評価することで後尾の並びを取り出す
-
サンクによるストリーム型の定義
var stream = { match: (data, pattern) => { return data(pattern); }, empty: (_) => { return (pattern) => { return pattern.empty(); }; }, cons: (head, tailThunk) => { return (pattern) => { return pattern.cons(head, tailThunk); }; }, /* head:: STREAM[T] => T */ /* ストリーム型headの定義は、リスト型headと同じ */ head: (aStream) => { return stream.match(aStream, { empty: (_) => { return null; }, cons: (value, tailThunk) => { return value; }, }); }, /* tail:: STREAM[T] => STREAM[T] */ tail: (aStream) => { return stream.match(aStream, { empty: (_) => { return null; }, cons: (head, tailThunk) => { return tailThunk(); // ここで初めてサンクを評価する }, }); }, take: (aStream, n) => { return stream.match(aStream, { empty: (_) => { return list.empty(); }, cons: (head, tailThunk) => { if (n === 0) { return list.empty(); } else { return list.cons(head, stream.take(tailThunk(), n - 1)); } }, }); }, }; /* 無限に1が続く数列 */ var ones = stream.cons(1, (_) => { return ones; // onesを再帰的に呼び出す });
-
- 関数の用途は、単に定義された計算を実行することだけではない
- 計算を実行するタイミングを操作することで、計算不能な手続きを計算可能にし、無限といった概念すら表現できるようになる
- 関数の引数を直ちに評価する方法を正格評価と呼ぶ
- 関数を定義する
- 関数と参照透過性
- 参照透過性とは、「評価される対象の構成要素がそっくり同じならば、その評価結果は同じ値である」という要請
-
var a = 10ならば、同じコンテキストのなかでは必ずaは10でなければならない - 関数における参照透過性とは、ある関数が同じ引数で呼び出されていれば必ず同じ値を返すという要請
-
- 入出力で参照透過性が破壊される
-
readFileSync関数が同じでも、ファイルが書き換えられていると同じ値は返らない - ファイルへの書き込みやファイルの読み込みなどの処理があるから
- これを関数が副作用を持つという
-
- 副作用とは何か
- データや変数が参照透過性を持つための条件とは
- いったん作られたデータと変数の関係を変更しないこと
- これはプログラミング言語の処理系が変数のスコープごとに環境を制御しているから可能となる
- プログラムを起動すると、処理系がコードや環境をメモリ上に展開してくれる
- 一方、副作用が影響を及ぼす対象は、処理系の外側に位置している(ファイル・ストレージ・画面・ネットワークなど)
- 処理系はその状態変化を管理できない
-
writeFile関数の副作用によってファイルの状態が変化しても、その状態変化がreadFile関数に伝えられることはない
- よって、入出力は処理系にとって隠れたコンテキストとして振る舞うことになる
- データや変数が参照透過性を持つための条件とは
- 参照透過性を破壊する条件
- データ: 可変なデータ(操作対象は記憶域)
- 変数: 代入操作(操作対象は記憶域)
- 関数: 副作用(操作対象は外界)
- 参照透過性を保証するための条件
- データは不変なデータのみを扱う
- 変数は、代入操作をせずにバインド操作のみに限定する
- 関数は副作用を使わない(純粋関数)
- 副作用への対処
- 副作用を完全に排除すると?
- そもそもユーザが計算の結果を画面で確認することすら不可能になる
- 画面は外界だから
- 副作用はコンピュータプログラムにとって必要な要素である
- なら、副作用とつきあう戦略は、副作用を適切に制御することとなる
- 副作用を分離し、副作用に伴う状態の変化をコード上で管理できる仕組みを作る
- そもそもユーザが計算の結果を画面で確認することすら不可能になる
- 副作用をコード上で管理する
-
状態を管理したreadFile関数
// 初期の状態s0では、/path/to/fileのファイルに // "あ"という文字が書き込まれているものとする // readFile関数によって状態s0から状態s1に移る var (content, s1) = readFile("/path/to/file", s0); // writeFile関数によって"い"を書き込み、状態s1から状態s2に移る var (undefined, s2) = writeFile("path/to/file", "い", s1); // readFile関数によって状態s2から状態s3に移る var (content, s3) = readFile("path/to/file", s2); /* 状態を管理したreadFile関数 */ readFile("/path/to/file", s0) === readFile("/path/to/file", s0) readFile("/path/to/file", s0) !== readFile("/path/to/file", s2) - これで参照透過性は保証できるが問題は多い
- 常に新しい状態を割り当てなければならない
- 必ず現在の状態をもとにして副作用のある関数を実行しなければならない
- モナドという仕組みで克服することができる
-
- 副作用を完全に排除すると?
- 参照透過性とは、「評価される対象の構成要素がそっくり同じならば、その評価結果は同じ値である」という要請
高階関数を活用する
- 高階関数とは何か
- Σ記号
- 微分
カリー化で関数を返す
- カリー化で関数を返す
- 複数の引数を持つ関数(多項関数)を1つの引数だけを持つ関数(1項関数)に変換すること
-
multipleOf関数をカリー化する例
/* multipleOf関数の定義 */ var multipleOf = (n, m) => { if (m % n === 0) { return true; } else { return false; } }; expect(multipleOf(2, 4)).to.eql(true); /* カリー化されたmultipleOf関数 */ var multipleOf = (n) => { return (m) => { if (m % n === 0) { return true; } else { return false; } }; }; expect(multipleOf(2)(4)).to.eql(true); /* multipleOfの簡約 */ multipleOf(2)(4) => { (m) => { if (m % 2 === 0) { // nが2に置換される return true; } else { return false; } }(4) } => if (4 % 2 === 0) { // mが4に置換される return true; } else { return false; } => true - カリー化関数の最大の特徴は、引数の一部だけを適用できる点である
- これを部分適用と呼ぶ
- カリー化関数はネストされた構造のため、パイプラインの中にパイプラインが入ったようなもの
- 部分適用によって返された関数は、独立した部品として利用することができる
-
multipleOf(2)は、引数が2の倍数であるかどうかを判定できる
var twoFold = multipleOf(2); expect(twoFold(4)).to.eql(true); - 同じようにして、
var threeFold = multipleOf(3);を作成できる
-
- 引数の順番には注意が必要
- 必ず左側の引数から順番に適用しなければならない
-
指数関数の例
var exponential = (base) => { return (index) => { if (index === 0) { return 1; } else { return base * exponential(base)(index - 1); } }; }; expect(exponential(2)(3)).to.eql(8);-
var square = exponential(2)としてしまうと、nの2乗ではなく、2のn乗になってしまう
-
- 引数の順番を逆転する高階関数があれば、この問題は解決する
-
flip関数の定義
var flip = (fun) => { return (x) => { return (y) => { return fun(y)(x); }; }; }; /* flipで引数を逆転させて、2乗を定義する */ var square = flip(exponential)(2); expect(square(3)).to.eql(4 /* 2 * 2 = 4 */); /* flipで引数を逆転させて、3乗を定義する */ var cube = flip(exponential)(3); expect(cube(2)).to.eql(8 /* 2 * 2 * 2 = 8 */);
-
- 関数とはデータを材料として製品を作り出す工場のようなもの
- 多項関数は、必要となる材料を一気に工場に流し込むような操作といえる
- 一方、カリー化関数は、工場をいくつものモジュールに分けたようなもの
- 部分適用により、ひとつひとつのモジュールを取り出すことができる
- カリー化によって関数を部品化すると、部分適用でその部品を様々に再利用可能になる
- チャーチ数について
- アロンゾ・チャーチは、カリー化を多用することで関数だけで自然数を定義できることを示した
- zeroは関数適用は0回、oneは1回だけなど
コンビネータで関数を組み合わせる
- コンビネータで関数を組み合わせる
- flip関数のように、関数を組み合わせるための高階関数を狭義のコンビネータと呼ぶ
-
notコンビネータによって、evenからodd関数を作り出す
var even = multipleOf(2); var not = (predicate) => { return (arg) => { return !predicate(arg); }; }; var odd = not(even); - 数学でいう関数の合成もコンビネータの1つ
-
関数合成の定義
var compose = (f, g) => { return (arg) => { return f(g(arg)); }; };
-
- そもそも関数とは処理を抽象化したもの
- 関数合成はその処理を組み合わせてより複雑な処理を構築する作用である
- 複雑な処理自体も1つの抽象なので、関数合成によって抽象のレベルを高められるということになる
-
関数合成が抽象のレベルを高める例
/* 具体的なlast関数: 再帰的にlast関数を呼び出して最末尾要素を返す */ var last = (alist) => { return list.match(alist, { empty: (_) => { return null; }, cons: (head, tail) => { return list.match(tail, { empty: (_) => { return head; }, cons: (_, _) => { return last(tail); }, }); }, }); }; /* 抽象的なlast関数: リストを逆転したものの先頭を返す */ var last = (alist) => { return compose(list.head, list.reverse)(alist); };-
compose関数で合成する段階ではデータ構造の詳細は隠蔽されている(抽象化)- リストの再帰処理も抽象化されている
- 再帰処理を多用する関数型プログラミングにおいて、この処理を隠蔽できることはシンプルさにつながる
- また、別の手法として畳み込み関数によっても抽象化できる
-
- Yコンビネータ
- 自分自身を適用するのがYコンビネータなので、再帰関数の原理と同じ
- 再帰を行う高階関数ということ
-
階乗を計算するfactorial関数を再帰関数を使わずに定義できる
/* Yコンビネータ */ var Y = (F) => { return ((x) => { return F((y) => { return x(x)(y); }); })((x) => { return F((y) => { return x(x)(y); }); }); }; /* Yコンビネータの簡約 */ // Y(F); // => F(Y(F)) // => F(F(Y(F))) // => F(F(F(Y(F)))) // > F(F(F(.....))) /* Yコンビネータによるfactorialの実装 */ var factorial = Y((fact) => { return (n) => { if (n === 0) { return 1; } else { return n * fact(n - 1); } }; }); expect( factorial(3) // 3 * 2 * 1 = 6 ).to.eql(6);
- 自分自身を適用するのがYコンビネータなので、再帰関数の原理と同じ
クロージャーを使う
- クロージャーを使う
- 関数と違って、クロージャーはプログラミングの世界に特有の用語
- 仕組みは、関数、環境、バインドで説明できる
- セマンティクスの世界を覗き込む必要がある
- クロージャーの仕組み
-
var foo = 1;で環境において変数をバインドできる- メモリ上に変数と値の対応が作成される
- これを環境と呼ぶ
- 関数適用の場合、仮引数と実引数の対応が新たに環境に追加される
-
バインドの例
var twoFold = multipleOf(2); expect(twoFold(4)).to.eql(true);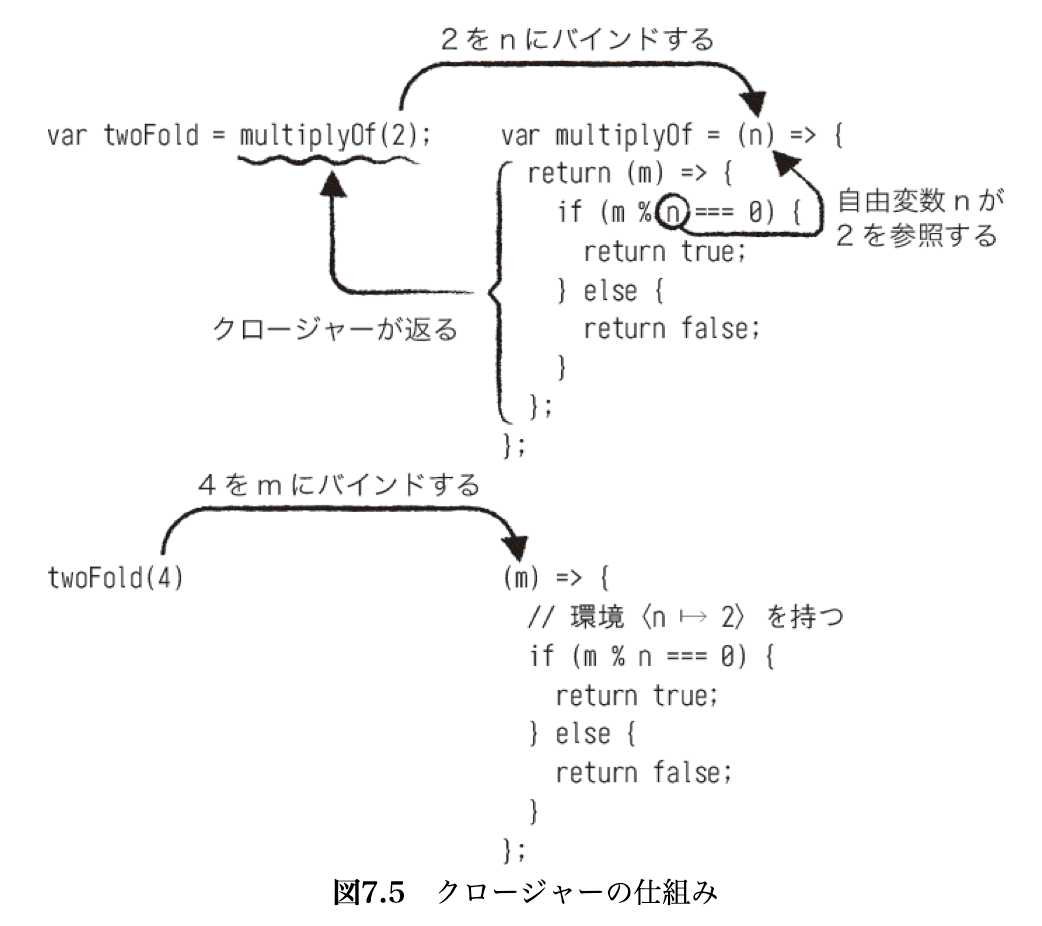
- 変数は自由変数だが、この変数は無名関数の外側のスコープに存在する変数nを参照することができる
- これは変数nに関する環境を包み込んだような関数と言える
- このように、定義された時点での環境を包み込んだ関数をクロージャー(closure)と呼ぶ
-
- クロージャーで状態をカプセル化する
- 関数がクロージャーを返すとき、クロージャー定義時に外側にあったスコープの変数を使うことができる
-
外側からcountingNumberにアクセスする手段はない(カプセル化)
/* クロージャーとしてのcounter関数 */ var counter = (init) => { var countingNumber = init; /* countingNumberの環境をもつクロージャーを返す */ return (_) => { countingNumber = countingNumber + 1; return countingNumber; }; }; /* counter関数の利用法 */ var counterFromZero = counter(0); expect(counterFromZero()).to.eql(1); expect(counterFromZero()).to.eql(2);
- クロージャーで不変なデータ構造を作る
- クロージャーが状態をカプセル化する機能を利用して、不変なデータ構造を作ってみる
- まずは、抽象データ型を作る(データをどう表現するかよりも、どのように操作するかという観点)
- 空のデータ構造を作る
- データ構造に値を入れて拡張する(構築子)
- データ構造から値を取得する
- 1と2が分かれているのは、データ構造に対する再帰的な処理を容易にするため
-
カリー化された不変なオブジェクト型
var object = { empty: (_) => { // 空のオブジェクトを意味する return null; }, set: (key, value) => { return (obj) => { // objのオブジェクトに対して、keyに対応するvalueを格納する return (queryKey) => { if (key === queryKey) { return value; } else { return object.get(queryKey)(obj); } }; }; }, get: (key) => { return (obj) => { // objのオブジェクトについて、keyに対応する値を取り出す return (obj) => { return obj(key) } }; }, };- データ構造がすべてクロージャーを用いて定義されている
- 外側のスコープにある3つの変数key、value、objを参照している

-
object.set("C3PO", "Star Wars")(object.empty())は、queryKeyを引数とするクロージャーを返す 
-
複数データを格納するためにcompose関数で合成する
var robots = compose( // object.setを合成する object.set("C3PO", "Star Wars"), object.set("HAL9000", "2001: a space odyssey") )(object.empty()); expect(object.get("HAL9000")(robots)).to.eql("2001: a space odyssey");
- データ構造がすべてクロージャーを用いて定義されている
- クロージャーで定義した理由
- objectのset関数で生成されたデータは、代入によって内容を更新することはできない
- 生成されたデータの実態は、クロージャーという名の関数だから
-
object.set("C3PO", "Star Wars")として生成されたデータ(実は関数)を、"C3PO"をキーとして"2001: a space odyssey"を値とするように変更することは不可能
- objectのset関数で生成されたデータは、代入によって内容を更新することはできない
- クロージャーでジェネレータを作る
- 汎用的なジェネレータの実装には、クロージャーとストリーム型を使用する
-
ストリームからジェネレータを作る
var generate = (aStream) => { /* いったんローカル変数にストリームを格納する */ var _stream = aStream; /* ジェネレータ関数が返る */ return (_) => { return stream.match(_stream, { empty: () => { return null; }, cons: (head, tailThunk) => { _stream = tailThunk(); // ローカル変数を更新する return head; // ストリームの先頭要素を返す }, }); }; };- 呼び出すたびにストリームから先頭のデータを1つずつ取り出して返す
-
整数列のジェネレータ
var integers = enumFrom(0); /* 無限ストリームからジェネレータを生成する */ var intGenerator = generate(integers); expect(intGenerator()).to.eql(0); expect(intGenerator()).to.eql(1); expect(intGenerator()).to.eql(2);- 関数適用のたびに無限の整数列の先頭から1つずつ整数を取り出して返す
-
エストステネスのふるいによる素数の生成
var sieve = (aStream) => { return stream.match(aStream, { empty: () => { return null; }, cons: (head, tailThunk) => { return stream.cons(head, (_) => { return sieve( stream.remove((item) => { return multipleOf(item)(head); })(tailThunk()) ); }); }, }); }; var primes = sieve(stream.enumFrom(2)); /* 素数のジェネレータ */ var primeGenerator = generate(primes);- 変数primesは無限の素数列になる
- クロージャーの純粋性
- クロージャーは純粋関数なのか?
- 定義によっていずれの場合もありえる
- 内部に変化しうる可変な状態を持つと、参照透過性が保てなくなる
- ただ、この不純なクロージャーはむしろ役に立つ場面もある
- テストに使用することで困難なチャーチ数のテストが可能になる
-
カウンターをクロージャーで定義する
expect(one(counter(0))()).to.eql(1); expect(two(counter(0))()).to.eql(2);
- クロージャーは純粋関数なのか?
- 関数と違って、クロージャーはプログラミングの世界に特有の用語
関数を渡す
- 関数を渡す
- コールバック関数で処理をモジュール化する
- 「電話をかけ直す = コールバックする」という言葉に由来する
- 着信にすぐさま出ないで、あとでかけ直す
-
直接的な呼び出しとコールバックの例
/* 直接的な呼び出しの例 */ var succ = (n) => { return n + 1; }; var doCall = (arg) => { return succ(arg); }; expect(doCall(2)).to.eql(3); /* 単純なコールバックの例 */ var setupCallback = (callback) => { /* コールバック関数を実行する無名関数を返す */ return (arg) => { return callback(arg); }; }; /* コークバック関数を設定する */ var doCallback = setupCallback(succ); expect(doCallback(2)).to.eql(3); - 違いは些細なものだが、結合度が違う
- 直接的に呼び出す例では、doCall関数とsucc関数は密に結合している
- doCall関数の挙動を変更するには、doCall関数そのものの定義を書き直す必要がある
- コールバックの例ではそれぞれの関数がモジュールとして独立しているため、組み合わせを返ることで異なる挙動を実現できる
-
var doCallback = setupCallback(opposite);とできる
-
- 直接的に呼び出す例では、doCall関数とsucc関数は密に結合している
- コールバック関数を利用するとモジュール性を高められる
- Node.jsなどでも使われている
- 「電話をかけ直す = コールバックする」という言葉に由来する
- 畳み込み関数に関数を渡す
- 関数型プログラミングでは、反復処理を再帰関数で実装するのが主流
- カウンター変数を隠蔽し、反復処理を抽象化できる
- まだ抽象化レベルは十分ではない
- リストの再帰処理を抽象化し、個々の要素に対する処理をコールバック関数として渡す手法
-
sum関数をコールバック関数を用いて再定義する
/* sum関数の定義 */ var list = { sum: (alist) => { return (accumulator) => { return list.match(alist, { empty: (_) => { return accumulator; }, cons: (head, tail) => { return list.sum(tail)(accumulator + head); }, }); }; }, }; /* コールバック関数を用いたsum関数の再定義 */ var list = { sumWithCallback: (alist) => { return (accumulator) => { // コールバック関数を受け取る return (CALLBACK) => { return list.match(alist, { empty: (_) => { return accumulator; }, cons: (head, tail) => { // コールバック関数を呼び出す return CALLBACK(head)( list.sumWithCallback(tail)(accumulator)(CALLBACK) ); }, }); }; }; }, }; var numbers = list.cons(1, list.cons(2, list.cons(3), list.empty())); /* sunWithCallback関数に渡すコールバック関数 */ var callback = (n) => { return (m) => { return n + m; }; }; expect(list.sumWithCallback(numbers)(0)(callback)).to.eql( 6 // 1 + 2 + 3 = 6 );
-
- リストに対する反復処理を抽象化した高階関数が畳み込み関数
-
リストの畳み込み関数
// 末尾のrはright var foldr = (alist) => { return (accumulator) => { return (callback) => { return list.match(alist, { empty: (_) => { return accumulator; }, cons: (head, tail) => { return callback(head)(foldr(tail)(accumulator)(callback)); }, }); }; }; }; 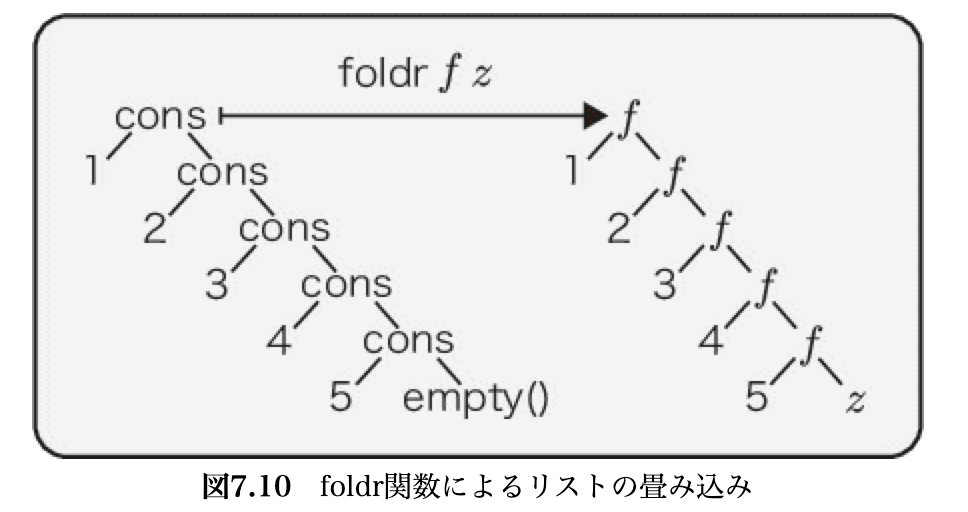
-
foldr関数によるsum関数とlength関数の定義
var sum = (alist) => { return foldr(alist)(0)((item) => { return (accumulator) => { return accumulator + item; }; }); }; var length = (alist) => { return foldr(alist)(0)((item) => { return (accumulator) => { return accumulator + 1; }; }); };
-
- foldr関数によって共通項を抽象化しつつ、蓄積変数の初期値とコールバック関数の組み合わせによって反復処理を具体化して、問題を解決している
- コールバック関数はfoldr関数とともに反復処理のモジュール化に貢献している
- JavaScriptにはこのfoldr関数の配列版である、reduceメソッドがある
- 関数型プログラミングでは、反復処理を再帰関数で実装するのが主流
- 非同期処理にコールバック関数を渡す
- 非同期処理を実行する仕組みがイベント駆動システム
- イベントループが各処理の実行のタイミングを制御している
- イベントループにコールバック関数が紐づけられている
- このコールバック関数をイベントハンドラと呼ぶ
- イベントがイベントループに到着すると、対応するイベントハンドラが実行されるようになっている
- 開発者はもっぱらイベントハンドラを定義してアプリケーションの挙動を制御する
- 例: レストランでの注文
- 注文から調理までの処理は非同期なので、待っている間にトイレに行ってもいい
- 非同期処理を実行する仕組みがイベント駆動システム
- 継続で未来を渡す
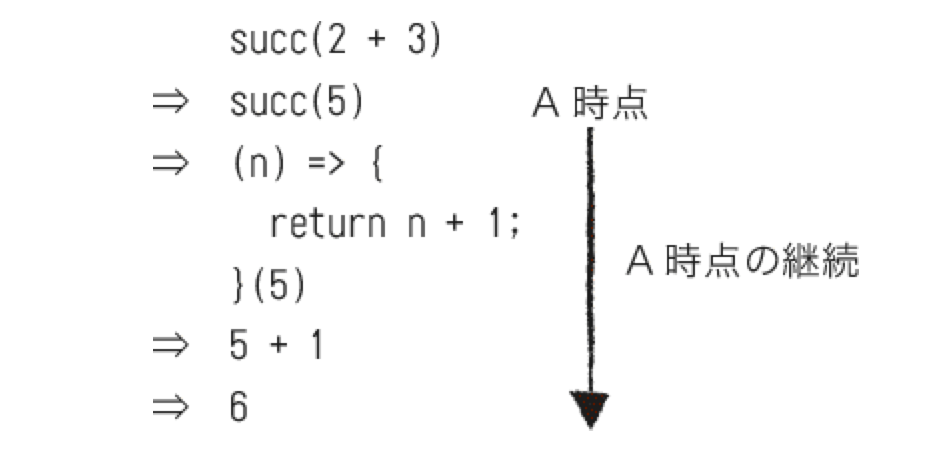
- 継続とは、ある時点の計算に続くすべての計算を意味する
- 例: 果てしない草原に1台のトロッコが走っている。トロッコとは、ある時点で実行されている計算であり、継続とは、トロッコの先に伸びている線路のこと。このときのA時点での継続とは、A時点から終着駅までの線路全体のこと
- 継続の基本形
-
継続の基本計
/* 継続渡しのsucc関数 */ var succ = (n, continues) => { return continues(n + 1); }; /* 継続渡しのsucc関数をテストする */ expect(succ(1, identity)).to.eql(2); /* 継続の基本形 */ var continues = (currentResult) => { // currentResultから得られた時点以降の全ての計算、すなわち継続を定義する };
-
- add(2, succ(3))の継続渡しの例
-
add(2, succ(3))の継続渡し
/* 継続渡しのsucc関数 */ var succ = (n, continues) => { return continues(n + 1); }; /* 継続渡しのadd関数 */ var add = (n, m, continues) => { return continues(n + m); }; /* 継続渡しのsucc関数とadd関数を使ってadd(2, succ(3))を計算する */ expect( succ(3, (succResult) => { return add(2, succResult, identity); }) ).to.eql(6); 
-
- トロッコはレールを辿るしかできないが、機能を追加することで枝分かれした未来を選ぶことや、過去に遡ることができる
- これは継続渡しで複数の継続を渡すことで実現できる
- 目的の要素が見つかったらすぐさま結果を返して終わるfind関数を実装する
-
継続による反復処理からの脱出find関数
/* 継続による反復処理からの脱出 */ var find = (aStream, predicate, continuesOnFailure, continuesOnSuccess) => { return list.match(aStream, { /* リストの最末尾に到着した場合、成功継続で反復処理を抜ける */ empty: () => { return continuesOnSuccess(null); }, cons: (head, tailThunk) => { /* 目的の要素を見つけた場合、成功継続で反復処理を脱出する */ if (predicate(head) === true) { return continuesOnSuccess(head); } else { /* 目的の要素を見つけられなかった場合、失敗継続で次の反復処理を続ける */ return continuesOnFailure( tailThunk(), predicate, continuesOnFailure, continuesOnSuccess ); } }, }); }; /* 成功継続では反復処理を脱出する */ var continuesOnSuccess = identity; /* 失敗継続では、反復処理を続ける */ var continuesOnFailure = ( aStream, predicate, continuesOnRecursion, escapesFromRecursion ) => { /* find関数を再帰的に呼び出す */ return find(aStream, predicate, continuesOnRecursion, escapesFromRecursion); }; /* 変数integersは、無限の整数ストリーム */ var integers = stream.enumFrom(0); /* 無限の整数列のなかから100を探す */ expect( find(integers, (item) => { return item === 100; }), continuesOnFailure, continuesOnSuccess ).to.eql(100); -
continuesOnSuccessは計算を終了させる成功継続で、continuesOnFailureは現時点での計算が失敗したあとの失敗継続となる
-
- 非決定性計算機を作る
- 通常の計算機は、計算が返す結果はただ1つしかないという意味で決定的
- 非決定性計算とは、複数の値を返すような計算
- 例: 1つの箱にはリンゴが1個入っていて、もう1つの箱にはリンゴは2個 or 3個入っていることしかわかっていない。このとき、2つの箱のリンゴの合計は、3個もしくは4個になる。このような計算を非決定性計算と呼ぶ
- 計算機の定義は、式の定義と評価関数の定義の2つで構成される
- 式は、数や関数などの計算の対象のこと
- 評価関数とは、式が与えられたとき、その式を計算する手順を定義した関数のこと
-
num(3)という式が与えられると、評価関数はその式を計算して数値3を返す
-
- 決定性計算機の例
-
決定性計算機
// 式の代数的データ構造 var exp = { // 代数的データ構造のパターンマッチ match: (anExp, pattern) => { return anExp.call(exp, pattern); }, // 数値の式 num: (n) => { return (pattern) => { return pattern.num(n); }; }, // 足し算の式 add: (exp1, exp2) => { return (pattern) => { return pattern.add(exp1, exp2); }; }, }; // 式の評価関数 var calculate = (anExp) => { return exp.match(anExp, { // 数値を評価する num: (n) => { return n; }, // 足し算の式を評価する add: (exp1, exp2) => { return calculate(exp1) + calculate(exp2); }, }); };
-
- 非決定性計算機の例
-
非決定性計算機の例
// 非決定計算機の式 var exp = { amb: (alist) => { return (pattern) => { return pattern.amb(alist); }; }, // 以下、決定性計算機のexpオブジェクトと同じ }; // 非決定性計算機の評価関数の骨格 var calculate = (anExp, continuesOnSuccess, continuesOnFailure) => { // 式に対してパターンマッチを実行する return exp.match(anExp, { num: (n) => { /* 数値を評価する */ return continuesOnSuccess(n, continuesOnFailure); // 数値nを渡す num(n)のあとの計算の失敗に備えて元の失敗継続を渡す }, add: (x, y) => { /* 足し算の式を評価する */ /* まず引数xを評価する */ return calculate( x, (resultX, continuesOnFailureX) => { /* 次に引数yを評価する */ return calculate( y, (resultY, continuesOnFailureY) => { /* 引数xとyがともに成功すれば、両者の値で足し算を計算する */ return continuesOnSuccess(resultX + resultY, continuesOnFailureY); }, continuesOnFailureX /* yの計算に失敗すれば、xの失敗継続を渡す */ ); }, continuesOnFailure /* xの計算に失敗すれば、おおもとの失敗継続を渡す */ ); }, amb: (choices) => { /* amb式を評価する */ var calculateAmb = (choices) => { return list.match(choices, { /* amb(list.empty())の場合、すなわち選択肢がなければ、失敗継続を実行する */ empty: () => { return continuesOnFailure(); }, /* amb(list.cons(head,tail))の場合、先頭要素を計算して、後尾は失敗継続に渡す */ cons: (head, tail) => { return calculate(head, continuesOnSuccess, (_) => { /* 失敗継続で後尾を計算する */ return calculateAmb(tail); }); }, }); }; return calculateAmb(choices); }, }); }; // 成功継続の一般形 var continuesOnSuccess = (result, continuesOnFailure) => { // 現在の計算が成功した場合に続く計算を定義する }; // 失敗継続の一般形 var continuesOnFailure = (_) => { // 現在の計算が失敗した場合に続く計算を定義する }; /* 非決定性計算機の駆動関数 */ var driver = (expression) => { /* 中断された計算を継続として保存する変数 */ var suspendedComputation = null; /* 成功継続 */ var continuesOnSuccess = (anyValue, continuesOnFailure) => { /* 最下位に備えて、失敗継続を保存しておく */ suspendedComputation = continuesOnFailure; return anyValue; }; /* 失敗継続 */ var continuesOnFailure = () => { return null; }; /* 内部に可変な状態suspendedComputationを持つクロージャーを返す */ return () => { /* 中断された継続がなければ、最初から計算する */ if (suspendedComputation === null) { return calculate(expression, continuesOnSuccess, continuesOnFailure); } else { /* 中断された継続があれば、その継続を実行する */ return suspendedComputation(); } }; }; /* 非決定性計算機のテスト */ /* amb[1,2] + amb[3,4] = 4,5,5,6 */ var ambExp = exp.add( exp.amb(list.fromArray([exp.num(1), exp.num(2)])), exp.amb(list.fromArray([exp.num(3), exp.num(4)])) ); var calculator = driver(ambExp); expect(calculator()).to.eql( 4 // 1 + 3 = 4 ); expect(calculator()).to.eql( 5 // 2 + 3 = 5 ); // ... expect(calculator()).to.eql( null // これ以上の候補はないので、計算は終了 ); - 継続渡しでは通常の処理の流れを超えて、独自の制御を作りだすという強力な機能がある
- プログラミング言語の奥のセマンティクスの領域で活用されている
- 継続渡し評価器と呼ばれる手法
-
- コールバック関数で処理をモジュール化する
モナドを作る
- モナドを作る
- モナドとは?
- もともとモナドは、参照透過性を維持したまま副作用を扱う手法としてHaskellに導入された
- 現在は副作用の制御だけでなく、エラー処理やデータベース用言語などでも活用されている
- 高階関数さえあれば、どのような言語でもモナドを扱える
- 高階関数を使った一種のデザインパターンだから
- モナドの機能
- 値にコンテキストを付加すること
- コンテキストを付加したまま処理を合成すること
- 例: 引越しをするために持ち物ひとつひとつを段ボールに詰めていく。梱包される物のひとつひとつが値である。そして物を入れるダンボールが、値を包みこむモナドとなる。
- もともとモナドは、参照透過性を維持したまま副作用を扱う手法としてHaskellに導入された
- モナドの基本
- 基本構造
- unit関数: モナドのインスタンスを生成するための関数
- クラスのコンストラクタと似たようなもの
- ただの値から、1個の単位としてモナドのインスタンスを作るための関数
-
unit:;T => M[T]という型情報を持つ - 引越しのたとえでは、持ち物を段ボールに詰める作業に該当する
- flatMap関数: 処理を合成するための関数
- モナドから値を取り出して、何らかの処理を施したあと、その結果を再びモナドに詰め込むための関数
- 引越しのたとえでは、「本」というラベルの付いた箱から1冊ずつ本を取り出して、引越し先の本棚に詰め込むという作業にあたる
- この途中で、それぞれの本に何らかの処理を施すことができる。1冊ずつ表紙をきれいに拭いてもいい
- flatMapの処理が終わると、本が入った段ボールは片付き、きれいな本を納めた本棚が残される
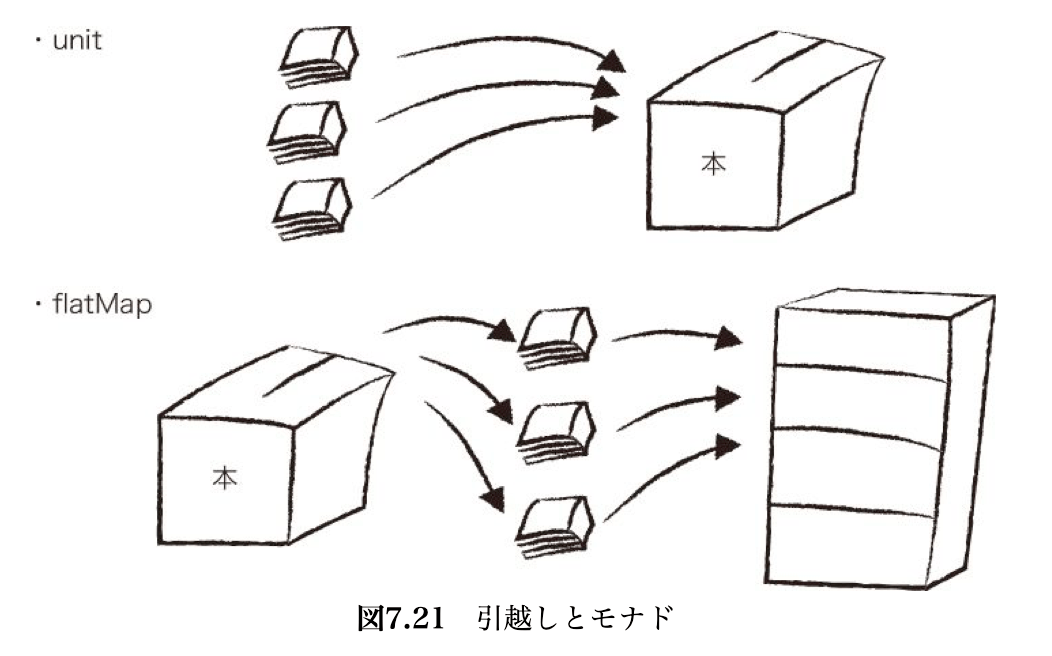
- unit関数: モナドのインスタンスを生成するための関数
- モナドの振る舞いとは、unit関数とflatMap関数の2つを適切に定義すること
- 3つの法則(モナド則)に従わないといけない
-
モナド側
// 右単位元則 flatMap(instanceM)(unit) === instanceM; // 左単位元則 flatMap(unit(value))(f) === f(value); // 結合法則 flatMap(flatMap(instanceM)(f))(g) === flatMap(instanceM)((value) => { return flatMap(f(value))(g); }); - 右単位元則
- モナドのインスタンスから値を取り出してunit関数を適用した結果は、元のモナドのインスタンスに等しい
- 引越しの例: 段ボールに入っている本を取り出して、その本をまた段ボールに詰めたものは、元の段ボールに等しい
- 左単位元則
- ある値から作られたモナドのインスタンスに対してflatMap関数を介してf関数を適用した結果は、元の値に対してf関数を適用した結果に等しい
- 引越しの例: f関数を「本にカバーをかけて段ボールに詰める」処理とすると、左単位元則は、「段ボールのなかにあるそれぞれの本にカバーをかけた結果は、単に本にカバーをかけた結果と同じになる」ということ
- 結合法則
- モナドという箱に入れていても関数適用について結合法則が成立する
- 引越しの例: g関数は「本をジャンルごとに分類して段ボールに詰める」処理とすると、「本にカバーをかけて段ボールに詰め、その段ボールの本をジャンルごとに分類して段ボールに詰める」という2段階の操作と、「本にカバーをかけて分類してから段ボールに詰める」という1段階の操作は同じということ
- 基本構造
- 恒等モナド
- 恒等モナドは、値にコンテキストを付加することなく、そのままの値として扱う
- 値を透明な箱に入れたようなもので、なかに入っている値は丸見え
- 引越しでいうと、本を段ボールに入れることなく、本のままで引越しするようなもの
- 実質的には何もしないが、他のモナドと比較する上で有益
- なんのコンテキストも付加していないので、モナドの骨格を知ることができる
-
恒等モナドの定義
var ID = { /* unit:: T => ID[T] */ unit: (value) => { // 単なるidentity関数と同じ return value; }, /* flatMap:: ID[T] => FUN[T => ID[T]] => ID[T] */ flatMap: (instanceM) => { return (transform) => { // 単なる関数適用と同じ return transform(instanceM); }; }, }; // unit関数はただ値を返しているだけ expect(ID.unit(1)).to.eql(1); // flatMapは単なる関数適用と同じ expect( ID.flatMap(ID.unit(1))((one) => { return ID.unit(succ(one)); }) ).to.eql(succ(1)); // flatMapと関数合成の類似性 expect( ID.flatMap(ID.unit(1))((one) => { /* succ関数を適用する */ return ID.flatMap(ID.unit(succ(one)))((two) => { /* double関数を適用する */ return ID.unit(double(two)); }); }) ).to.eql(compose(double, succ)(1));
- 恒等モナドは、値にコンテキストを付加することなく、そのままの値として扱う
- Maybeモナドでエラーを処理する
- 正常な値を
just(value)、エラーの場合をnothing()と表現する -
Maybeモナド
/* Maybeの代数的構造 */ var maybe = { match: (exp, pattern) => { return exp.call(pattern, pattern); }, just: (value) => { return (pattern) => { return pattern.just(value); }; }, nothing: (_) => { return (pattern) => { return pattern.nothing(_); }; }, }; /* Maybeモナドの定義 */ var MAYBE = { unit: (value) => { return maybe.just(value); }, flatMap: (instanceM) => { return (transform) => { return maybe.match(instanceM, { /* 正常な値の場合は、transform関数を計算する */ just: (value) => { return transform(value); }, /* エラーの場合は、何もしない */ nothing: (_) => { return maybe.nothing(); }, }); }; }, /* ヘルパー関数 */ getOrElse: (instanceM) => { return (alternate) => { return maybe.match(instanceM, { just: (value) => { return value; }, nothing: (_) => { return alternate; }, }); }; }, }; /* 足し算を定義する */ var add = (maybeA, maybeB) => { return MAYBE.flatMap(maybeA)((a) => { return MAYBE.flatMap(maybeB)((b) => { return MAYBE.unit(a + b); }); }); }; var justOne = maybe.just(1); var justTwo = maybe.just(2); expect(MAYBE.getOrElse(add(justOne, justOne))(null)).to.eql(2); expect(MAYBE.getOrElse(add(justOne, maybe.nothing())))(null).to.eql(null);- flatMap関数の定義として、Maybeモナドのコンテキストが計算に反映されている
- add関数の定義では、エラー処理を一切行っていない
- コードは単にa + bを計算しているだけ
- Maybeモナドは何を行っているのか
- Maybeモナドはunit関数で値を包み込むとき、その値に正常化異常かのコンテキストを付加する
- もし計算式のどこかにnothing()があれば、計算式全体がnothing()を返す
- このため、異常な場合コード上で無視することができる
- 引越しの例: 引越しの機会に不要な本を捨ててしまい、大切な本だけ持っていく場合、Maybeモナドを使わなければ、引越し元で捨てるべき本かどうかを判断し、さらに引越し先でも毎回捨てるべき本かどうかを確認しないといけなくなる。Maybeモナドを使うと、捨てるべき本かどうかを一度決めてしまうと、引越し先での処理は残した本だけに対して実行されるようになる
- 正常な値を
- IOモナドで副作用を閉じ込める
- IOモナドの意義
- 副作用を持つ不純なコードをモナドの内部に閉じ込めることができる
- これにより純粋な関数と副作用を持つ処理とを、きれいに分離することができる
- flatMap関数によってIOアクションを合成することができる
- 低レベルな入出力アクションを組み合わせて、豊かなIOアクションの作成が可能になる
- 結局、副作用を関数という部品のなかに閉じ込めて、さらにそれらの部品を組み合わせる手段を用意しているということ
- 副作用を持つ不純なコードをモナドの内部に閉じ込めることができる
- 副作用の制御が難しいのは、副作用の対象が処理系の外側に位置するから
- もし副作用を一種のコンテキストと捉えれば、モナドによって表現できるはず
- IOモナドの仕組み
- 副作用を伴う計算は、計算結果を返すだけでなく外界の状態を変化させる
- 画面出力はディスプレイの画素の状態を変化させ、データベース操作はファイルの内容を変更する
- この外界というコンテキストをモナドで包み込む
-
FUN[WORLD => PAIR[T, WORLD]]: WORLDが外界の型で、Tは外界が包み込む値の型 - IOモナドが関数型として表現されているのは、副作用を伴う計算がそれまでの外界を前提として新しい外界を作りだす操作だから
- Piar型:
pair.right(tuple)とpair.left(tuple)で左右の値を取り出せる
-
- 副作用を伴う計算は、計算結果を返すだけでなく外界の状態を変化させる
-
IOモナド
/* Pair型の定義 */ var pair = { // pairの代数的データ構造 cons: (left, right) => { return (pattern) => { return pattern.cons(left, right); }; }, match: (data, pattern) => { return data(pattern); }, // ペアの右側を取得する right: (tuple) => { return this.match(tuple, { cons: (left, right) => { return right; }, }); }, // ペアの左側を取得する left: (tuple) => { return this.match(tuple, { cons: (left, right) => { return left; }, }); }, }; /* 外界を明示したIOモナドの定義 */ var IO = { // unit:: T => IO[T] unit: (any) => { // 引数worldは現在の外界 return (world) => { return pair.cons(any, world); }; }, // flatMap:: IO[A] => (A => IO[B]) => IO[B] flatMap: (instanceA) => { // actionAB:: A -> IO[B] return (actionAB) => { return (world) => { /* 現在の外界のなかでinstanceAのIOアクションを実行する */ var newPair = instanceA(world); return pair.match(newPair, { cons: (value, newWorld) => { /* 新しい外界のなかで、actionAB(value)で作られた IOアクションを実行する */ return actionAB(value)(newWorld); }, }); }; }; }, /* done:: T => IO[T] done関数 */ done: (any) => { return IO.unit; }, /* run:: IO[A] => A */ run: (instanceM) => { return (world) => { /* IOアクションを現在の外界に適用し、結果のみを返す */ return pair.left(instanceM(world)); }; }, /* readFile:: STRING => IO[STRING] readFile関数は、pathで指定されたファイルを読み込むIOアクション */ readFile: (path) => { // 外界を引数とする return (world) => { var fs = require("fs"); var content = fs.readFileSync(path, "utf8"); // 外界を渡してIOアクションを返す return IO.unit(content)(world); }; }, /* println:: STRING => IO[] println関数は、messageで指定された文字列を コンソール画面に出力するIOアクション */ println: (message) => { // IOモナドを返す return (world) => { console.log(message); return IO.unit(null)(world); }; }, }; /* run関数の利用法 */ var initialWorld = null; expect(IO.run(IO.println("吾輩は猫である"))(initialWorld)).to.eql(null); /* 外界を明示しないIOモナドの定義 */ var IO = { /* unit:: T => IO[T] */ unit: (any) => { // 外界を指定しない return (_) => { return any; }; }, /* flatMap:: IO[A] => FUN[A => IO[B]] => IO[B] */ flatMap: (instanceA) => { return (actionAB) => { /* instanceAのIOアクションを実行し、 続いてactionABを実行する */ return actionAB(IO.run(instanceA)); }; }, /* done:: T => IO[T] */ done: (any) => { return IO.unit(); }, /* run:: IO[A] => A */ run: (instance) => { return instance(); }, /* readFile:: STRING => IO[STRING] */ readFile: (path) => { var fs = require("fs"); return IO.unit(fs.readFileSync(path, "utf8")); }, /* println:: STRING => IO[] */ println: (message) => { console.log(message); return IO.unit(); }, }; /* run関数の利用法 */ expect( /* 外界を指定する必要はありません */ IO.run(IO.println("名前はまだない")) ).to.eql(null);- 生成されたIOモナドのインスタンスは、IOアクションと呼ばれる
- IOアクションを評価することで、実際の入出力処理が行われる
- 生成されたIOモナドのインスタンスは、IOアクションと呼ばれる
- IOアクションを合成する
- 粒度の細かいIOアクションを準備しておき、flatMap関数でそれらのIOアクションを合成する
- 合成のコード例
- putChar関数を定義し、それを合成して文字列を出力するputStr関数を作る
- 1文字だけを出力する原始的な関数から始まり、それを徐々に組み合わせて最終的にputStrLn関数を作り上げる
- putChar関数を定義し、それを合成して文字列を出力するputStr関数を作る
- IOモナドの意義
- モナドとは?
関数型言語を作る
- JavaScript上で関数型言語の処理系を作ってみる
- ファーストクラスオブジェクトとしての関数を備え、カリー化関数やクロージャーを可能とする
- モナドによって関数型言語の評価器をモジュール化し、機能を拡張しやすくする
- プログラミング言語の仕組み
- 関数型言語を実装する試みは、一見車輪の再発明だが、言語の仕組みを理解する上で重要なこと
- 処理系の挙動を決定づけるセマンティクスの領域は、コードから直接的には見えない
- 処理系を作るという作業は、それまで「見えないもの」であった言語のセマンティクスを、コードという「見えるもの」として明らかにする学習上のメリットがある
- プログラミング言語の処理には、大きく分けて2つの段階がある
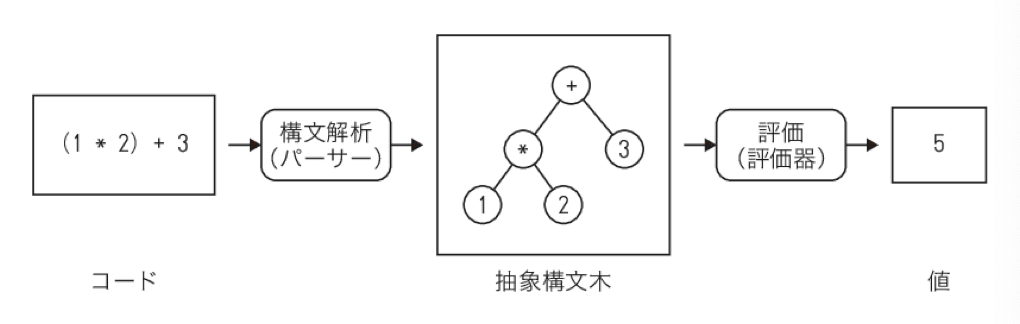
- 1つ目: 文字の並びであるコードを解釈して、コンピュータが処理しやすいデータ構造に変換する
- 文字の並びのルールをシンタックスと呼ぶ
- 日本語の文章では、日本語の文法がシンタックスに相当する
- 処理系はまずコードがシンタックスに合致していることを確認して、コードを抽象構文木という内部表現に変換する
- この段階を構文解析と呼ぶ
- 構文解析を実行する関数をパーサーと呼ぶ
- 文字の並びのルールをシンタックスと呼ぶ
- 2つ目: 抽象構文木を解釈して答えを計算する
- この作用を評価(evaluate)と呼ぶ
- それを実行する関数を評価器と呼ぶ
- この評価器が前提とするのが、言語のセマンティクスと呼ばれる領域
- 処理系はセマンティクスをもとにして抽象構文木を評価する
- セマンティクスに従って計算する評価器こそが、プログラミング言語処理系のエンジンとなる
- シンタックスとセマンティクスの違い
- 日付の計算の例
- 「1989-1-8」と「西暦1989年1月8日」は異なるシンタックスを持っているが、いずれも意味するところは平成元年の最初の日
- 最初の4桁は西暦、次は月、最後は日付を表すというデータへの意味付けが必要
- この意味付けこそがセマンティクスと呼ばれる領域
- 「1989-1-8」と「西暦1989年1月8日」は異なるシンタックスを持っているが、いずれも意味するところは平成元年の最初の日
- 日付の計算の例
- プログラミング言語の処理系は、まず構文解析を実行して抽象構文木を求め、その次に評価器で抽象構文木から結果を計算する
- 言語処理系の処理:
compose(evaluate, parse)(source)
- 言語処理系の処理:
- 関数型言語を実装する試みは、一見車輪の再発明だが、言語の仕組みを理解する上で重要なこと
- 抽象構文木を作る
- 処理系の開発では最初に式を設計する
- 式とは計算の対象となるコードのこと
- 数値を表す1や、関数を表す
(n) => { return n + 1; }などが式を表す - 数値、変数、関数定義、関数適用を基本的な式とする
- 処理系の開発では最初に式を設計する
- 環境を作る
- 式を評価するには、原則として変数と値の対応を記憶した環境が必要
- 環境には3つの操作が不可欠
- 空の環境を作る操作
- 環境に変数と値の対応を与えて、環境を拡張する操作
- 変数を指定して、環境に記憶されている値を取り出す操作
- 「環境」モジュールのコード例
- 処理系の実装では、見えない環境を明示的にコード化する必要がある
- 変数バインディングにおける「環境」の働きのコード例
- クロージャーにおける「環境」の働きのコード例
- 評価器を作る
- 関数型モデルにおける計算とは、置き換えルールに従って式を簡約し、値を得ること
- 置き換えルール: ラムダ式の定義の際に関数本体に現れた仮引数を適用時の実引数に置換する
- この置換ルールこそが、関数型言語の基本的なセマンティクス
- このセマンティクスに従って式を簡約する関数を、評価関数と呼ぶ
- 式ごとに評価関数が定義され、すべての式の評価関数を集めたものがその言語の評価器となる
- 個々の評価関数は、式と環境をもとにして式を評価する
-
evaluate::(EXP, ENV) => M[VALUE]: Mはモナドの型
-
- 恒等モナドによる評価器のコード例
- ログ出力評価器のコード例
- LOGモナドの定義により、flatMap関数に計算の過程でログを追加する機能が付加される
- モナドを用いた評価器では、使うモナドを変更して、新しく追加した式の評価関数を定義するだけでログ出力の機能が付加できる
- これこそが、モナドが評価器にもたらしたモジュール化の成果
- 関数型モデルにおける計算とは、置き換えルールに従って式を簡約し、値を得ること
Discussion