Zenn
🗺️

いびつな形の市区町村を探す [Python+GeoJSON+OpenCV]

2022/09/12に公開
Python
OpenCV
Streamlit
#
geojson
tech

題材

時々見ているYouTubeチャンネル「おもしろ地理」さんで、変わった形の市区町村が話題になっていました。
https://twitter.com/omoshirochiri/status/1536972764535574528?s=20&t=qJKWBP9taN1m5BUAsAuFGA

こういうことを計算で探してみましょう。

そもそも昔から形には興味がありました。1日数時間Google Mapsを眺めても飽きない性分です。

細長いとかちぎれそうなど、尺度はいろいろあると思いますが、今回はでこぼこした、いびつな形を狙ってみました。なお地理は好きですが、GeoJSON等の技術面は素人です。

成果物 (Streamlit)

Streamlitで作りました。都道府県ごとにいびつ度合いのランキングで見られます。（本記事ではStreamlitの説明は省きます。）

https://shimat-municipality-shape-main-jbp2e1.streamlitapp.com/

実装はこちら。
https://github.com/shimat/municipality_shape

実行結果の例

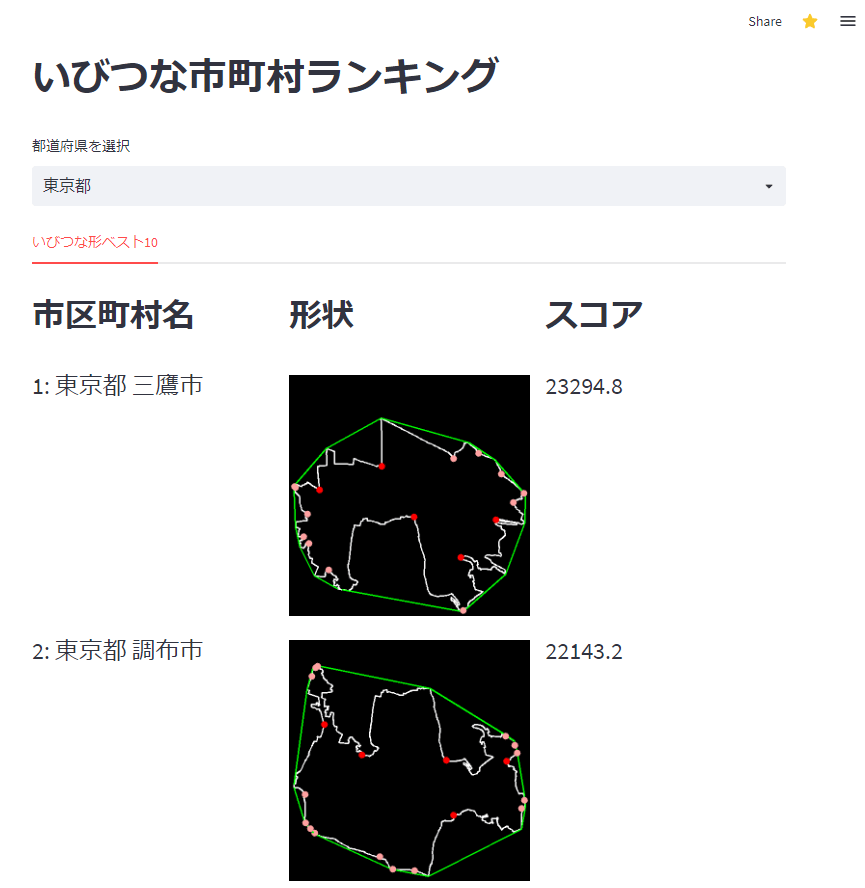
要素技術

  • 市区町村の輪郭データを得る
  • 緯度経度で表される輪郭データを平面直角座標系に変換する
  • 輪郭の凸性欠陥(Convexity Defects)により「いびつさ」を計算する

データ出典

基本的に使用したのは上のリンクから進んだ先の、各市区町村のGeoJSONデータです。

実装

1. GeoJSONから輪郭を得る

ここから参照します。https://geoshape.ex.nii.ac.jp/city/code

以下、小樽市の例を整形して引用します。json["features"][0]["geometry"]["coordinates"]に輪郭の座標(緯度経度)データがあり、今回はそれのみ扱います。

{
    "type": "FeatureCollection",
    "id": "gci:01203A1968",
    "metadata": {
        "type": ["行政区境界"],
        "dc:title": "北海道小樽市:フル解像度GeoJSON",
        ...
    },
    "features": [{
        "type": "Feature",
        "properties": { ... },
        "geometry": {
            "type": "MultiPolygon",
            "coordinates": [
                [
                    [
                        [141.13040745, 43.15353576],
                        [141.13035964, 43.15353155],
                        [141.13031184, 43.15354417],
                        [141.13030228, 43.1535694],
                        [141.13030228, 43.15359464],
                        [141.13031184, 43.15361566],
                        [141.13033096, 43.15361987],
                        [141.13042657, 43.15361566],
                        [141.13046481, 43.15361146],
                        [141.13048393, 43.15359464],
                        [141.13048393, 43.15357361],
                        [141.13046481, 43.15355258],
                        [141.13040745, 43.15353576]
                    ]
                ],
                [
                    [
                        [141.13078986, 43.15352735],
                        [141.13075162, 43.15351052],
			...
                    ],
		    ...
		],
		...
            ]
        }
    }]
}

141.13040745, 43.15353576 のように経度, 緯度の数値が入っています。輪郭は1つとは限らないことに注意します。例えば以下のようなケースで2つ以上の輪郭があります。

  • 海岸線がある (島・岩・防波堤・埋立地等)
  • 飛び地がある

とはいえ、素人ゆえちょっと意図が分からなかったのですが、coordinatesの配列は1段余計に深い気がしまして、itertools.chain.from_iterableで1階層だけ平坦化しています。

import itertools
import json

with open("01203.geojson", "r", encoding="utf-8") as f:
    geojson = json.load(f)

coordinates: list[list[list[list[float]]]] = geojson["features"][0]["geometry"]["coordinates"]
contours: list[list[list[float]]] = list(itertools.chain.from_iterable(coordinates))

2. 緯度・経度から平面直角座標系に変換する

（ここが素人です）

緯度・経度は、地球という球面上の位置であり、このあとの輪郭関係の処理を行うにはややこしいです。"普通"の平面上の座標に変換していきます。

緯度の1度と経度の1度は、距離が違います。最初はこのことすら忘れていました。例えば北緯40度では、経度1度が約85kmに対し、緯度1度は約111kmとのことです。「緯度経度のまま適当に整数に正規化すれば何とかなるだろう」というわけにもいかないほど歪みます。
https://www.wingfield.gr.jp/archives/9721

座標変換にはpyprojを使いました。
https://pypi.org/project/pyproj/
https://pyproj4.github.io/pyproj/stable/

from pyproj import Transformer

transformer = Transformer.from_proj(4326, 6679)
lon, lat = 141.13040745, 43.15353576
y, x = transformer.transform(lat, lon)
print(x, y)  # 71603.2948640449 -93659.86489432973

4326 6679 というマジックナンバーが出てきていますが、これはEPSGコードです。変換元, 変換先 の順で指定します。例えば以下が参考になります。

https://qiita.com/XPT60/items/9aa41cab07ce6369fb99#epsg

4326のほうはWGS 84を表し、これは固定で良い（はず）です。6679のほうは場所により異なります。以下国土地理院のページで説明されるように、日本では場所によって19種類の平面直角座標系が定義されています。[1]
https://www.gsi.go.jp/sokuchikijun/jpc.html
https://www.gsi.go.jp/LAW/heimencho.html

以下は抜粋です。今回の例では「小樽市」が対象だったので、系番号XIを使うというのがわかります。XIは EPSG:6679 に対応します。
Transformer.transformの出力が71603.2948640449 -93659.86489432973のような値でしたが、これもリストを見れば原点 東経140度15分0秒0000, 北緯44度0分0秒0000からのずれを表すとわかります。

系番号 経度（東経） 緯度（北緯） 適用区域
XI 140度15分0秒0000 44度0分0秒0000 小樽市　函館市　伊達市　北斗市　北海道後志総合振興局の所管区域　北海道胆振総合振興局の所管区域のうち豊浦町、壮瞥町及び洞爺湖町　北海道渡島総合振興局の所管区域　北海道檜山振興局の所管区域

ここまでをまとめ、geojsonで得た輪郭の緯度経度座標列に対する、平面直角座標への変換処理の例です。Transformerの引数は緯度(latitude)・経度(longitude)の順であり、GeoJSONと逆なので注意します。

import itertools
import json
from pyproj import Transformer


with open("geojson/01203.geojson", "r", encoding="utf-8-sig") as f:
    geojson = json.load(f)

coordinates: list[list[list[list[float]]]] = geojson["features"][0]["geometry"]["coordinates"]
contours_lonlat: list[list[list[float]]] = list(itertools.chain.from_iterable(coordinates))

transformer = Transformer.from_proj(4326, 6679)
contours_xy: list[list[tuple[float, float]]] = [
    [transformer.transform(lat, lon)[::-1] for lon, lat in contour] 
    for contour in contours_lonlat]
"""
[[(71603.2948640449, -93659.86489432973), (71599.41138484543, -93660.3734320976),  ...], 
[(71634.40614952768, -93660.4721603153), (71631.31574200565, -93662.37443090997), ...], ...
]
"""

都道府県・市区町村名からEPSGを得るコード

前述のこの定義をPythonに書き起こしたものです。任意の自治体名で処理したい際に使います。

from pyproj import Transformer

WGS84 = 4326
PREF_TO_COORD_NUMBER = {
    "長崎県": 1,
    "福岡県": 2, "佐賀県": 2, "熊本県": 2, "大分県": 2, "宮崎県": 2,
    "山口県": 3, "島根県": 3, "広島県": 3,
    "香川県": 4, "愛媛県": 4, "徳島県": 4, "高知県": 4,
    "兵庫県": 5, "鳥取県": 5, "岡山県": 5,
    "京都府": 6, "大阪府": 6, "福井県": 6, "滋賀県": 6, "三重県": 6, "奈良県": 6, "和歌山県": 6,
    "石川県": 7, "富山県": 7, "岐阜県": 7, "愛知県": 7,
    "新潟県": 8, "長野県": 8, "山梨県": 8, "静岡県": 8,
    "福島県": 9, "栃木県": 9, "茨城県": 9, "埼玉県": 9, "千葉県": 9, "群馬県": 9, "神奈川県": 9,
    "青森県": 10, "秋田県": 10, "山形県": 10, "岩手県": 10, "宮城県": 10,
}
NUMBER_1_CITIES = {
    "十島村", "喜界町", "奄美市", "龍郷町", "大和村", "宇検村", "瀬戸内町",
    "天城町", "徳之島町", "伊仙町", "和泊町", "知名町", "与論町"
}
NUMBER_11_CITIES = {
    "小樽市", "函館市", "伊達市", "北斗市",
    "島牧村", "寿都町", "黒松内町", "蘭越町", "ニセコ町", "真狩村", "留寿都村", "喜茂別町", "京極町", "俱知安町", "共和町", "岩内町",
    "泊村", "神恵内村", "積丹町", "古平町", "仁木町", "余市町", "赤井川村",
    "豊浦町", "壮瞥町", "洞爺湖町",
    "松前町", "福島町", "知内町", "木古内町", "七飯町", "鹿部町", "森町", "八雲町", "長万部町",
    "江差町", "上ノ国町", "厚沢部町", "乙部町", "奥尻町", "今金町", "せたな町",
}
NUMBER_13_CITIES = {
    "北見市", "帯広市", "釧路市", "網走市", "根室市",
    "美幌町", "津別町", "斜里町", "清里町", "小清水町", "訓子府町", "置戸町", "佐呂間町", "大空町",
    "音更町", "士幌町", "上士幌町", "鹿追町", "新得町", "清水町", "芽室町", "中札内村", "更別村", "大樹町", "広尾町", "幕別町",
    "池田町", "豊頃町", "本別町", "足寄町", "陸別町", "浦幌町",
    "釧路町", "厚岸町", "浜中町", "標茶町", "弟子屈町", "鶴居村", "白糠町",
    "別海町", "中標津町", "標津町", "羅臼町",
    "色丹村", "泊村", "留夜別村", "留別村", "紗那村", "蘂取村",
}
NUMBER_14_CITIES = {
    "小笠原村"
}
NUMBER_16_CITIES = {
    "宮古島市", "多良間村", "石垣市", "竹富町", "与那国町",
}
NUMBER_17_CITIES = {
    "北大東村", "南大東村"
}

def get_transformer(pref: str, city: str) -> Transformer:
    """
    自治体名から、使うべきpyproj.Transformerを返す
    """
    number = get_coordinate_system_number(pref, city)
    epsg = get_epsg(number)
    return Transformer.from_proj(WGS84, epsg)


def get_epsg(coordinate_system_number: int) -> int:
    """
    平面直角座標系の番号 (I,II,III,...,XIX) から、EPSGコードを返す
    """
    return 6668 + coordinate_system_number


def get_coordinate_system_number(pref: str, city: str) -> int:
    """
    自治体名から、使うべき平面直角座標系コード(I, II, III, ..., XIX)を返す
    """
    if result := PREF_TO_COORD_NUMBER.get(pref):
        return result

    if pref == "鹿児島県":
        if city in NUMBER_1_CITIES:
            return 1
        return 2
    if pref == "東京都":
        if city in NUMBER_14_CITIES:
            return 14
        return 9
        # 沖ノ鳥島(18), 南鳥島(19)は小笠原村だが、父島で代表させるので該当なし
    if pref == "北海道":
        if city in NUMBER_11_CITIES:
            return 11
        if city in NUMBER_13_CITIES:
            return 13
        return 12
    if pref == "沖縄県":
        if city in NUMBER_16_CITIES:
            return 16
        if city in NUMBER_17_CITIES:
            return 17
        return 15

    raise ValueError(f"Not expected municipality: {pref=}, {city=}")


if __name__ == "__main__":
    x = get_coordinate_system_number("福岡県", "福岡市")
    print(x)  # 2

3. 座標を適当な整数値に正規化する

ここまでに得た平面直角座標系の値は、負の数もある、絶対値が数万など、まだ扱いづらい状態です。画像処理的アプローチに落とし込むために、0から500の整数値に正規化することにします (500は適当に定める数値)。

なおnumpyも素人ですが、気を付けた箇所は以下です。

  • すべての輪郭点についてxとyの最大最小値を求め、それを基準にmin-max正規化をします。形が崩れないよう、xとyで同じ引き延ばし係数を使うようにします。
  • y座標について、「緯度」は上(北)方向が正ですが、ラスタ画像においては(大抵は)下方向が正です。そのままでは南北逆になった輪郭になるので、500 - yする格好で反転させます。
import itertools
import numpy as np
import numpy.typing as npt
import cv2


def get_minmax(contours: list[list[tuple[float]]]) -> tuple[float, float, float, float]:
    flat = list(itertools.chain.from_iterable(contours))
    array = np.array(flat)
    x, y = array.T
    xmin, xmax, _, _ = cv2.minMaxLoc(x)
    ymin, ymax, _, _ = cv2.minMaxLoc(y)
    return xmin, xmax, ymin, ymax

   
def normalize_minmax(
        coordinates: npt.NDArray,
        xmin: float, xmax: float, ymin: float, ymax: float,
        size: int,
        border_size: int,
        dtype: np.dtype = np.int32
) -> npt.NDArray:
    x, y = coordinates.T
    if (xmax - xmin) > (ymax - ymin):
        scale = (xmax - xmin)
    else:
        scale = (ymax - ymin)
    normx = ((x-xmin)/scale) * (size - border_size*2)
    normy = ((y-ymin)/scale) * (size - border_size*2)
    result = np.vstack([normx + border_size, size - normy - border_size]).T
    return result.astype(dtype)
  
  
# (中略)
contours_xy: list[list[tuple[float, float]]] = [ ... ]

xmin, xmax, ymin, ymax = get_minmax(contours_xy)
normalized_contours: list[npt.NDArray] = [
    normalize_minmax(np.array(contour), xmin, xmax, ymin, ymax, 500, 10) 
    for contour in contours_xy]

うまくできているか、数値が多すぎてよくわからないので描画してみましょう。[2]

img_contours = np.zeros((500, 500, 1), np.uint8)
cv2.polylines(img, normalized_contours, isClosed=True, color=(255, 255, 255), thickness=1)
cv2.imwrite("otaru.png", img)

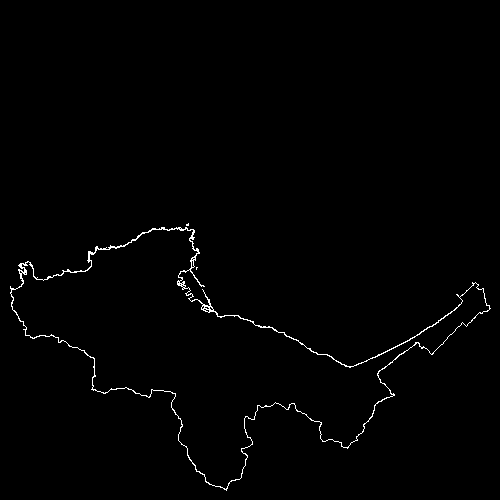
小樽の輪郭

4. 凸性欠陥で"いびつ度"を数値化してみる

ここまでで普通の画像処理的な範疇に落とし込むことができました。残りはOpenCVで攻めます。

いびつ度合いをどう数値化するか。様々考えられると思いますが、今回はConvexity Defectsを使うことにしました。上位5位までのへこみの平均値をスコアにします。

「凸性欠陥」と日本語では言われるようです。以下のページなどが参考になります。

要は輪郭のへこみを調べます。先に出力結果を示します。

緑色の線はConvex Hull (凸包) と呼ばれる、輪郭の点をすべて包含する最小の凸多角形です。輪ゴムをピンと張って輪郭の外側に引っ掛けた時の形です。そしてConvexity Defectsは赤やピンクの点で示され、Convex Hullからへこんだ部分です。赤がへこみ上位5番目までです。

上の画像のような出力が得られる、Convex HullとConvexity Defectsを求めて描画するコードです。

normalized_contours: list[npt.NDArray] = [ ... ]

largest_contour: npt.NDArray[np.int32] = sorted(normalized_contours, key=lambda c: cv2.contourArea(c), reverse=True)[0]
hull: npt.NDArray[np.int32] = cv2.convexHull(largest_contour, returnPoints=False)
hull[::-1].sort(axis=0)  # https://github.com/opencv/opencv/issues/4539#issuecomment-766798290
defects: list[list[npt.NDArray[np.int32]]] = cv2.convexityDefects(largest_contour, hull)

img_hull = cv2.cvtColor(img_contours, cv2.COLOR_GRAY2BGR)
sorted_defects = sorted((defects[i, 0] for i in range(defects.shape[0])), key=lambda x: x[3], reverse=True)

for i, (s, e, f, d) in enumerate(sorted_defects):
    start = largest_contour[s]
    end = largest_contour[e]
    far = largest_contour[f]
    cv2.line(img_hull, start, end, color=(0, 255, 255), thickness=2)
    color = (0, 0, 255) if i < 5 else (160, 160, 255)
    cv2.circle(img_hull, far, radius=7, color=color, thickness=-1)

cv2.imwrite("otaru_cd.png", img_hull)

ここで、上のコードでいう d が、へこみの奥までの近似距離を示しています。dの上位5件の平均を取ってスコアを求めます。

score = np.average([d for _, _, _, d in sorted_defects[:5]])
print(score)  # 14688.2

ということで、小樽市のいびつ度は14688.2でした。

結果発表

栄えある1位は、「岩手県大船渡市 (28470.4)」でした。

2位は「北海道旭川市 (28241.8)」。

共通するのは、手のひら型ですね。5つくらいのへこみがあり、上位5件の平均を取るという尺度に狙い撃ちしている形状です。

以下の三重県志摩市は、なかなかのいびつさですがスコア23074.6と振るいませんでした。これはConvex Hullの限界を感じます。「へこみの中のさらにへこみ」に対応できません。

こちらは「神奈川県横浜市中区」です。スコア19512.4と振るいません。志摩市同様に、へこみを全部Convexity Defectsと判断できていない様子がわかります。かつ、下の埋め立て地の島(南本牧ふ頭)がノーカウントです。実装では(さらっと)最大面積の輪郭で処理するように書いたので抜け落ちます。この島・飛び地の問題は厄介です。ノーカウントの分だけ大きさ[3]が目減りして、スコアが低下します。海沿いだけでなく、平成の大合併により内陸でも飛び地自治体が増えています。どうしたものか。

とはいえ、だいたいは「変な形」の市区町村が上位になりました。適当に書いたにしては満足です。

そのほか、都道府県ごとに結果が見られますので、見てみてください。[4]
https://shimat-municipality-shape-main-jbp2e1.streamlitapp.com/

脚注

  1. 間違えて指定すると歪みますが、ぱっと見では気づかない程度ではあります。 ↩︎

  2. 中央に寄せる処理はサボっています。 ↩︎

  3. 実際の市区町村の面積ではなく、正規化して求めた座標値による面積 ↩︎

  4. 全国ランキング表示は、Streamlit Community Cloudのメモリ1GB制限にひっかかりやすく断念しています。 ↩︎

Discussion