Zenn
📏

【Processing】なんちゃって3Dで遊ぼう ～行列による座標変換～

2022/12/08に公開
Processing
3d
tech

はじめに

2Dの画面に3Dを描画することにロマンを感じませんか．私は感じます．描きましょう．

なお，「なんちゃって3D」とタイトルにあるのは，遠くのものが小さく見えるような処理がないからです．ガチガチの3Dモデルを描きたい！という方が求めるようなものはない可能性が高いですし，厳密性には欠けるかもしれません．

また，この記事は長野高専アドベントカレンダー2022の8日目の記事です．

環境

ジェネラティブアートの作品にしばしば使われるProcessingを使います．ProcessingはJavaベースの記法で簡単に図形を描画することができます．ダウンロードしてついてくるexeファイルを実行すればIDEが立ち上がり，すぐにコードを実行できます．

余談ですが，長野高専の情報技術研究部ではProcessingを用いてプログラミング入門しています．

原理

座標系

今回は，processingのxy平面に奥行きzを追加した座標系を考えます．すなわち，

  • x軸の正の方向は右
  • y軸の正の方向は下
  • z軸の正の方向は奥

の座標系の世界で考えます．

正面から見る

画面上で，手前から奥がz軸の方向になるわけですが，画面はもちろん平面であり，z座標の違いを表現しなければ手前と奥がわかりません．今回はこの違いを表現することを諦めます．
今回の手法は点(1,2,3)を描画したいときは(1,2)に点を打ちます．(1,2,5)を描画する場合も(1,2)に点を打ちます．つまり，z座標は完全に無視をします．
もちろん，この方法で描画すると現実ではあり得ないような立体の見え方になってしまいます．z座標が全く違う場所に同じ形の立体を置いても，大きさの差が全く現れません．遠近法とかそんなものはありません．なんちゃって3Dだからいいのです[1]．

別の角度から見る

各辺が各座標軸と平行な立方体を先程の手法で描画すると，ただの正方形が描かれます．「これは真正面から見た立方体です！3Dです！」と主張するのは無理がありますね．しかし，斜めから見た場合を描画するのは簡単ではないです．そこで，別の角度から見た場合の処理は諦めます．代わりに，立体自身が回転してもらいます．視点が動くのではなく，見えてる物体が動き，実質視点が動いているように見える，という状態です．自分が動いているのではない，世界が動いているんだ．

z軸周りの回転

では，ここから回転をさせる方法を考えていきます．いきなり立方体を回転させるのは難しいので，点を回転させることを考えます．立体図形は点の集まりだと考えれば良いです．立方体であれば，8つの頂点があります．これらのそれぞれの点について回転させて，それらの点をつなげることで，回転した立方体が完成します．

まず，z軸中心に点を回転したときの様子を数式で表します．
z軸中心に点を回転させても，そのz座標が変わらないので，これはxy平面の世界の回転だと考えることができます．
z軸周りで\gammaだけ回転されると座標(x_0,y_0)は次のような座標(x,y)に移動します．

x = x_0\cos \gamma - y_0\sin \gamma \\\\ y = x_0\sin \gamma + y_0\cos \gamma

なぜこうなるかは，ベクトルの(x_0,0)と(0,y_0)を回転させることを考えるとわかります．(x_0,0)は\gamma回転すると(x_0\cos \gamma,x_0\sin \gamma)に，(0,y_0)は(-y_0\sin \gamma,y_0\cos \gamma)に移動します．(x_0,0)と(0,y_0)を足したベクトル(x_0,y_0)を\gamma回転させた結果は，(x_0,0)と(0,y_0)をそれぞれ\gamma回転させてから足したものと等しいです．よって上記の式が示せます．

x,y軸周りの回転

z軸周りのときのx,yをy,zとかz,xに置き換えれば良いです[2]．
x軸周りに\alpha回転したときは

y = y_0\cos \alpha - z_0\sin \alpha \\\\ z = y_0\sin \alpha + z_0\cos \alpha

y軸周りに\beta回転したときは

z = z_0\cos \beta - x_0\sin \beta \\\\ x = z_0\sin \beta + x_0\cos \beta

で表されます．

行列での表現

行列で表現しておくと，行列の積によって回転の組み合わせが行えるため，便利です．このような行列を回転行列と呼びます．

A_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & - \sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{pmatrix} \\\\ A_y(\beta) = \begin{pmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{pmatrix} \\\\ A_z(\gamma) = \begin{pmatrix} \cos \gamma & - \sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{pmatrix}

座標X=^t\!(1,2,3)をz軸周りに90^\circ回転させたい場合，A_z(90^\circ)をXの左から掛け算します．具体的には次の計算をします．

A_z(90^\circ)X = \begin{pmatrix} \cos 90^\circ & - \sin 90^\circ & 0 \\ \sin 90^\circ & \cos 90^\circ & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \\ 3 \\ \end{pmatrix}

z軸周りに90^\circ回転させて，さらにx軸周りに30^\circ回転させた座標は，A_x(30^\circ)A_z(90^\circ)Xで表されます．左から掛け算されていることに注意です[3]．

平行移動

原点から離れた場所に立体を置いてから回転させると，回転の軸が原点を通っているため立体の場所が移動します．これは，その場で回転させたい場合に不便です．その場合は，

  1. 原点中心に立体を配置
  2. 欲しい角度に回転させる
  3. 平行移動させる

のステップが必要です．面倒ですね．スッキリさせたいです．
行列の次元数を1増やして定数を足すテクニックを使い，次のように平行移動も行列で表現します．

\begin{pmatrix} 1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_0 \\ y_0 \\ z_0 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} x_0 + d_x \\ y_0 + d_y \\ z_0 + d_z \\ 1 \\ \end{pmatrix}

x軸周りに\alpha回転させて(d_x,d_y,d_z)だけ平行移動させた座標は次のようになります．

\begin{pmatrix} 1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & - \sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_0 \\ y_0 \\ z_0 \\ 1 \\ \end{pmatrix}

左の2つの行列の積を事前に計算しておくことで，\alpha回転させて(d_x,d_y,d_z)平行移動させるような行列が得られるため，あとはこれを掛け算するだけで一連の移動が可能になります．頂点が複数ある立体を移動させるときに便利です．

このように行列の積を扱うことで，平行移動させて回転させて平行移動させて回転させて...みたいな複雑な座標変換も可能です．複数のオブジェクトを配置したあとに，視点を移動させるためにさらに平行移動と回転を加える，といったことができます．

このように座標を表すベクトルに行列を掛け算させるて座標を移動させることを座標変換といい，その行列のことを変換行列と呼びます．また，この掛け算をベクトルに変換行列を作用させる，といいます．

実装

4次の正方行列に関する次の機能を作ります．行列は4\times 4のfloat型の配列で作ります．

  • 行列の積
  • 単位行列の生成
  • 各軸周りの回転行列の生成
  • 平行移動するための変換行列の生成
行列に関するプログラム
float[][] MatrixMul(float A[][], float B[][]) {
  float [][] Mat = new float [4][4];
  for (int i=0; i<4; i++) {
    for (int j=0; j<4; j++) {
      for (int k=0; k<4; k++) {
        Mat[i][j] += A[i][k]*B[k][j];
      }
    }
  }
  return Mat;
}

float[][] MatrixI() {
  float [][] Mat = new float [4][4];
  Mat[0][0] = 1;
  Mat[1][1] = 1;
  Mat[2][2] = 1;
  Mat[3][3] = 1;
  return Mat;
}


float[][] MatrixRotateX(float a) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = 1;
  Mat[1][1] = cos(a);
  Mat[1][2] = -sin(a);
  Mat[2][1] = sin(a);
  Mat[2][2] = cos(a);
  Mat[3][3] = 1;
  return Mat;
}

float[][] MatrixRotateY(float a) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = cos(a);
  Mat[0][2] = sin(a);
  Mat[1][1] = 1;
  Mat[2][0] = -sin(a);
  Mat[2][2] = cos(a);
  Mat[3][3] = 1;
  return Mat;
}

float[][] MatrixRotateZ(float a) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = cos(a);
  Mat[0][1] = -sin(a);
  Mat[1][0] = sin(a);
  Mat[1][1] = cos(a);
  Mat[2][2] = 1;
  Mat[3][3] = 1;
  return Mat;
}

float[][] MatrixMove(Vector3D v) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = 1;
  Mat[1][1] = 1;
  Mat[2][2] = 1;
  Mat[3][3] = 1;
  Mat[0][3] = v.x;
  Mat[1][3] = v.y;
  Mat[2][3] = v.z;
  return Mat;
}


void printMatrix(float[][] mat) {
  for (int i=0; i<4; i++) {
    for (int j=0; j<4; j++) {
      print(mat[i][j]);
      print(", ");
    }
    print("\n");
  }
}

また，3次元の点が扱えるようにVector3Dクラスを作ります．行列を作用させた点を返すactMatrixメソッドも作っておきます．

Vector3Dクラス

class Vector3D {
  float x, y, z;
  Vector3D(float _x, float _y, float _z) {
    this.x = _x;
    this.y = _y;
    this.z = _z;
  }
  Vector3D actMatrix(float Mat[][]) {
    Vector3D p = new Vector3D(0, 0, 0);
    p.x = this.x * Mat[0][0] + this.y * Mat[0][1] + this.z * Mat[0][2] + Mat[0][3];
    p.y = this.x * Mat[1][0] + this.y * Mat[1][1] + this.z * Mat[1][2] + Mat[1][3];
    p.z = this.x * Mat[2][0] + this.y * Mat[2][1] + this.z * Mat[2][2] + Mat[2][3];
    return p;
  }
}

グローバル変数として，transformMatrixを用意してます．各描画関数では3次元の点を受け取り，この行列transformMatrixを作用させて得られる点を使って描画するようにします．次の例ではline3D関数を実装しています．また，時間tもグローバル変数として用意しておきます．

グローバル変数とline3D関数
float transformMatrix[][] = new float [4][4];
float t = 0;

void line3D(Vector3D p1, Vector3D p2) {
  Vector3D a1 = p1.actMatrix(transformMatrix);
  Vector3D a2 = p2.actMatrix(transformMatrix);
  //ellipse(a1.x, a1.y, 10, 10); 頂点
  //ellipse(a2.x, a2.y, 10, 10);
  line(a1.x, a1.y, a2.x, a2.y);
}

あとはdraw関数に適当な内容を書いて完成です．

適当な内容
void draw(){;
  t += 1;
  background(0);
  translate(width/2, height/2);
  
  int s = 50;
  transformMatrix = MatrixI();
  float mat1[][] = MatrixRotateX(t*0.1);
  float mat2[][] = MatrixRotateY(t*0.1);
  transformMatrix = MatrixMul(mat2, transformMatrix);
  transformMatrix = MatrixMul(mat1, transformMatrix);

  Vector3D p1 = new Vector3D(-s, -s, s);
  Vector3D p2 = new Vector3D(-s, s, s);
  Vector3D p3 = new Vector3D(s, s, s);
  Vector3D p4 = new Vector3D(s, -s, s);
  Vector3D p5 = new Vector3D(-s, -s, -s);
  Vector3D p6 = new Vector3D(-s, s, -s);
  Vector3D p7 = new Vector3D(s, s, -s);
  Vector3D p8 = new Vector3D(s, -s, -s);
  stroke(255);
  strokeWeight(3);
  line3D(p1, p2);
  line3D(p2, p3);
  line3D(p3, p4);
  line3D(p4, p1);
  line3D(p5, p6);
  line3D(p6, p7);
  line3D(p7, p8);
  line3D(p8, p5);
  line3D(p1, p5);
  line3D(p2, p6);
  line3D(p3, p7);
  line3D(p4, p8);
}

遊ぶ

キーボード(WASD)を押すと正八面体を回転させることができるサンプルです．
コピペで動きます．

コード全体
float t = 0;
float transformMatrix[][] = new float [4][4];
float alpha=0, beta=0, gamma=0;


float[][] MatrixMul(float A[][], float B[][]) {
  float [][] Mat = new float [4][4];
  for (int i=0; i<4; i++) {
    for (int j=0; j<4; j++) {
      for (int k=0; k<4; k++) {
        Mat[i][j] += A[i][k]*B[k][j];
      }
    }
  }
  return Mat;
}

float[][] MatrixI() {
  float [][] Mat = new float [4][4];
  Mat[0][0] = 1;
  Mat[1][1] = 1;
  Mat[2][2] = 1;
  Mat[3][3] = 1;
  return Mat;
}


float[][] MatrixRotateX(float a) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = 1;
  Mat[1][1] = cos(a);
  Mat[1][2] = -sin(a);
  Mat[2][1] = sin(a);
  Mat[2][2] = cos(a);
  Mat[3][3] = 1;
  return Mat;
}

float[][] MatrixRotateY(float a) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = cos(a);
  Mat[0][2] = sin(a);
  Mat[1][1] = 1;
  Mat[2][0] = -sin(a);
  Mat[2][2] = cos(a);
  Mat[3][3] = 1;
  return Mat;
}

float[][] MatrixRotateZ(float a) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = cos(a);
  Mat[0][1] = -sin(a);
  Mat[1][0] = sin(a);
  Mat[1][1] = cos(a);
  Mat[2][2] = 1;
  Mat[3][3] = 1;
  return Mat;
}

float[][] MatrixMove(Vector3D v) {
  float [][] Mat = new float [4][4];
  Mat[0][0] = 1;
  Mat[1][1] = 1;
  Mat[2][2] = 1;
  Mat[3][3] = 1;
  Mat[0][3] = v.x;
  Mat[1][3] = v.y;
  Mat[2][3] = v.z;
  return Mat;
}


void printMatrix(float[][] mat) {
  for (int i=0; i<4; i++) {
    for (int j=0; j<4; j++) {
      print(mat[i][j]);
      print(", ");
    }
    print("\n");
  }
}


class Vector3D {
  float x, y, z;
  Vector3D(float _x, float _y, float _z) {
    this.x = _x;
    this.y = _y;
    this.z = _z;
  }
  Vector3D actMatrix(float Mat[][]) {
    Vector3D p = new Vector3D(0, 0, 0);
    p.x = this.x * Mat[0][0] + this.y * Mat[0][1] + this.z * Mat[0][2] + Mat[0][3];
    p.y = this.x * Mat[1][0] + this.y * Mat[1][1] + this.z * Mat[1][2] + Mat[1][3];
    p.z = this.x * Mat[2][0] + this.y * Mat[2][1] + this.z * Mat[2][2] + Mat[2][3];
    return p;
  }
}

void line3D(Vector3D p1, Vector3D p2) {
  Vector3D a1 = p1.actMatrix(transformMatrix);
  Vector3D a2 = p2.actMatrix(transformMatrix);
  ellipse(a1.x, a1.y, 10, 10);
  ellipse(a2.x, a2.y, 10, 10);
  line(a1.x, a1.y, a2.x, a2.y);
}

void ellipse3D(Vector3D p,float r){
  Vector3D a = p.actMatrix(transformMatrix);
  ellipse(a.x, a.y, r , r);
}




void setup() {
  size(500, 500);
  frameRate(50); // 50fpsでアニメーションする
}



void draw() {
  t += 0.1;
  background(0);
  translate(width/2, height/2);
  for(int i=1;i<=1;i++){
    int s = 70 + i*50;
    transformMatrix = MatrixI();
    float mat1[][] = MatrixRotateY(i*PI/2+alpha);
    float mat2[][] = MatrixRotateX(beta);
    float mat3[][] = MatrixRotateZ(gamma);
    transformMatrix = MatrixMul(mat1, transformMatrix);
    transformMatrix = MatrixMul(mat2, transformMatrix);
    transformMatrix = MatrixMul(mat3, transformMatrix);
    stroke(255);
    Vector3D p1 = new Vector3D (s,s,0);
    Vector3D p2 = new Vector3D (s,-s,0);
    Vector3D p3 = new Vector3D (-s,-s,0);
    Vector3D p4 = new Vector3D (-s,s,0);
    Vector3D p5 = new Vector3D (0,0,sqrt(2)*s);
    Vector3D p6 = new Vector3D (0,0,-sqrt(2)*s);
    line3D(p1,p2);
    line3D(p2,p3);
    line3D(p3,p4);
    line3D(p4,p1);
    line3D(p1,p5);
    line3D(p2,p5);
    line3D(p3,p5);
    line3D(p4,p5);
    line3D(p1,p6);
    line3D(p2,p6);
    line3D(p3,p6);
    line3D(p4,p6);
  }
      
}

void keyPressed(){
  if(key == 'd'){
    alpha += 0.1;
  }
  if(key == 'a'){
    alpha -= 0.1;
  }
  if(key == 'w'){
    beta += 0.1;
  }
  if(key == 's'){
    beta -= 0.1;
  }
}

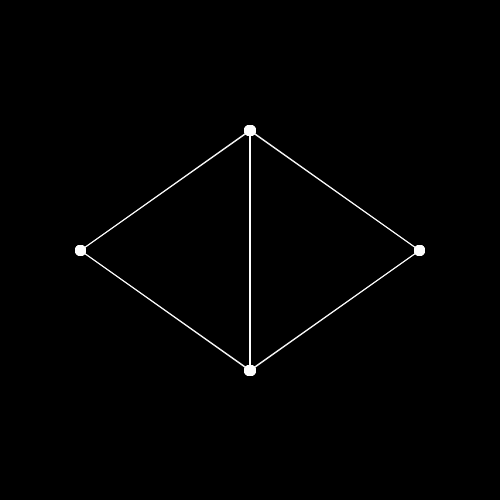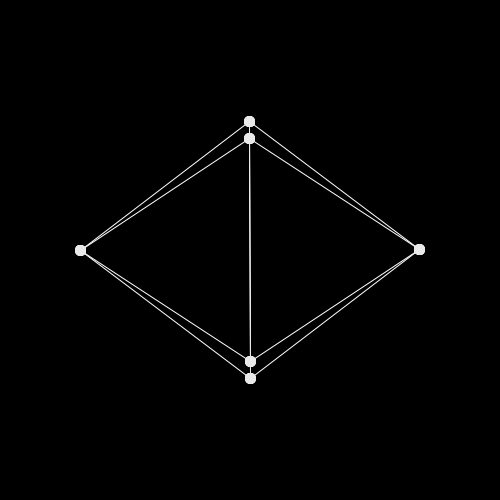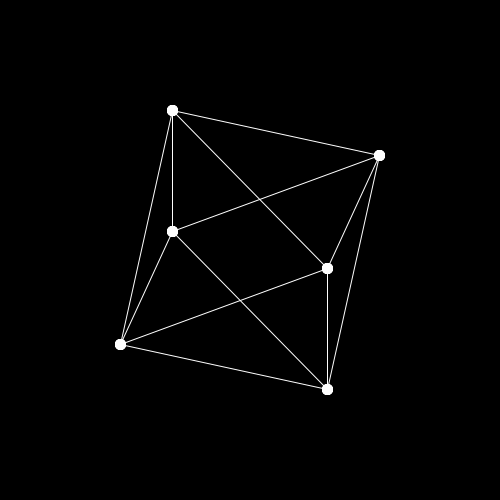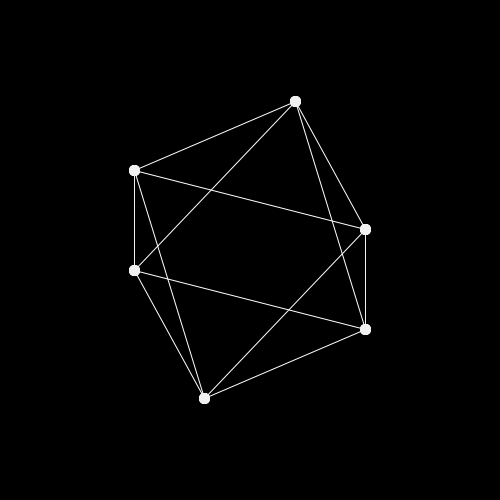
余談

こちらのつぶやきProcessingは回転行列を作用させるような計算をして作りました．
https://twitter.com/Shibak33333333n/status/1418192071987400713

あとがき

3Dで描画できる環境を使えばいい話なのですが，ロマンがありますね．

脚注

  1. なんちゃって3Dとか書いてしまいましたが，製図の分野などで，キャビネット図や等角図という名前で使われます． ↩︎

  2. 厳密には，どちらが正の方向の回転であるかをよく考える必要がありますが，今回は無視します ↩︎

  3. Xを列ベクトルではなく行ベクトルとして用意することで右から行列を掛け算する流派(この場合は回転行列が転置します)も存在します． ↩︎

Discussion