🌪️

生成AI時代こそ有用「風が吹けば桶屋が儲かる」をPythonで因果推論してみた 〜擬似相関と交絡因子の罠 vs 因果〜

に公開
Python
統計学
データサイエンス
MLOps
因果推論
tech

はじめに

「風が吹けば桶屋が儲かる」

あまりにも有名なこのことわざ、エンジニアやデータサイエンティストの視点で見ると、ひとつの疑問が湧いてきませんか？

「それ、本当に因果関係あるの？ ただの相関（あるいは擬似相関）じゃない？」

今回はこの疑問を解消するために、Python を使って以下の実験を行ってみました。

  1. 相関の罠: データだけ見ると「風と売上」に強い相関がある状態を作る。
  2. 真実の解明: 統計解析（回帰分析）で、その相関が見せかけであることを暴く。
  3. 構造の自動発見: ベイズネットワークを用いて、データから勝手に「真の因果グラフ（DAG）」を描かせる。

特に 3 つ目の「構造学習」では、アルゴリズムが 「風と桶屋は他人である」 と看破する様子が可視化され、非常に面白い結果になりました。

生成 AI にデータを丸投げして示唆出しを要求することの 愚かさ がわかるはずです。
ここに人間が因果推論含むデータサイエンスを学ぶ 真の価値 があると気づけると思っています。

今回のアーキテクチャ（検証環境）

https://github.com/shayate811/causal-inference

「手元の環境では動いたけど、ライブラリのバージョンが上がって動かなくなった」という"データ分析あるある"を防ぐため、今回は Dev Containers を導入し、完全な再現性を担保しました。

特に因果推論ライブラリ pgmpy はアップデートによる API 変更が激しいため、requirements.txt 内でバージョンを厳密に固定（Pinning）しています。

  • Language: Python 3.11
  • Libraries:
    • pgmpy==0.1.25 (Version Pinned)
    • pandas, statsmodels, networkx
  • Environment: Docker (Dev Containers)

1. データの生成：「真犯人」を仕込む

まず、ことわざの裏にある「真のメカニズム」を以下のように仮定してダミーデータを生成します。

  • 真の構造: 「風」が「桶屋」を儲けさせるのではない。「気温（冬の寒さ）」 が共通の原因（交絡因子）である。
    • 寒くなる \to 北風が強くなる（風速 UP）
    • 寒くなる \to 乾燥して桶が壊れる \to 買い替え需要（売上 UP）

つまり、風速と売上の間に直接的な因果関係はありません。

data_generation.py
import numpy as np
import pandas as pd

np.random.seed(42)
n_samples = 2000

# 共通の原因（交絡因子）：気温
temperature = np.random.normal(0, 1, n_samples)

# 気温が低いほど風が強い（負の相関）+ ノイズ
wind_speed = -0.7 * temperature + np.random.normal(0, 2.0, n_samples)

# 気温が低いほど桶が売れる（負の相関）+ ノイズ
# ★重要: ここに wind_speed は一切関係していない！
barrel_sales = -0.8 * temperature + np.random.normal(0, 2.0, n_samples)

df = pd.DataFrame({
    'Temperature': temperature,
    'Wind_Speed': wind_speed,
    'Barrel_Sales': barrel_sales
})

2. 罠にかかる：単純な相関確認

まずは何も知らないふりをして、「風速」と「売上」の関係を単回帰分析（OLS）で見てみます。

import statsmodels.api as sm

X = sm.add_constant(df['Wind_Speed'])
y = df['Barrel_Sales']
model = sm.OLS(y, X).fit()
print(model.summary())


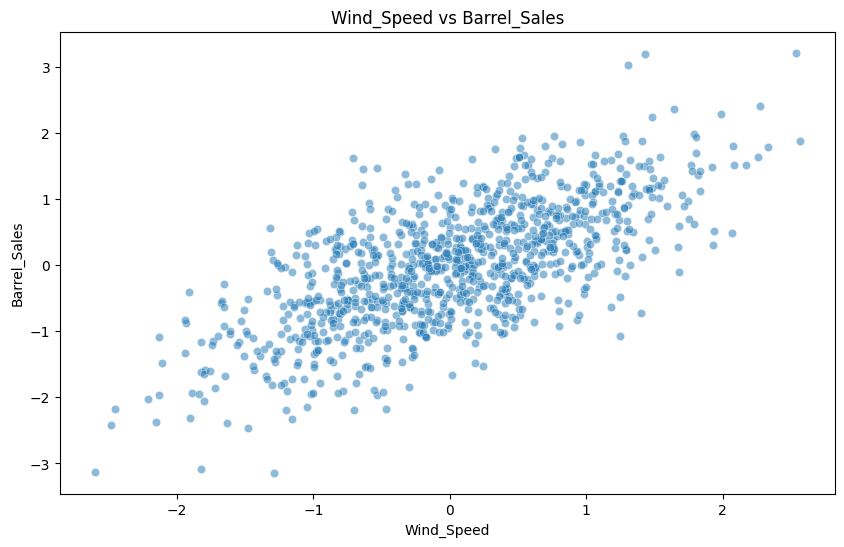
風速と売上の単純相関係数: 0.686

結果はどうなるでしょうか？相関係数: 正の値を観測 P 値: 0.000 (P < 0.05)統計的に 「有意に相関がある」という結果が出ました。データだけを見れば「風が吹けば桶屋が儲かる」は正しいように見えてしまいます。これが擬似相関（Spurious Correlation） の罠です。

3. ネタばらし：交絡因子の統制

次に、真の黒幕である「気温（Temperature）」をモデルに加えて重回帰分析を行います。

X = sm.add_constant(df[['Wind_Speed', 'Temperature']])
model = sm.OLS(y, X).fit()

すると、驚くべき変化が起きます。

--- Model 1: 単回帰分析 (売上 ~ 風速) ---
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         -0.0285      0.021     -1.350      0.177      -0.070       0.013
Wind_Speed     0.7271      0.024     29.779      0.000       0.679       0.775
==============================================================================

--- Model 2: 重回帰分析 (売上 ~ 風速 + 気温) ---
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
const           0.0031      0.016      0.197      0.844      -0.028       0.034
Wind_Speed     -0.0102      0.031     -0.326      0.745      -0.071       0.051
Temperature    -0.7962      0.028    -28.890      0.000      -0.850      -0.742
===============================================================================

Temperature の係数: 有意な値を示す。

Wind_Speed の係数: ほぼ 0 になり、P 値が大きく（有意でなく）なる。

「気温」という情報を固定して考えると、「風」は「売上」に対して何の影響も与えていないことが統計的に証明されました。

4. 構造学習：データから「設計図」を逆算する

ここからが本題です。 人間が「気温が怪しい」と仮説を立てなくても、コンピューター自身にデータの構造（因果グラフ）を発見させることはできるでしょうか？

Python のライブラリ pgmpy を使い、ベイズネットワークの構造学習（Structure Learning）を行ってみます。

from pgmpy.estimators import HillClimbSearch, BicScore
import networkx as nx
import matplotlib.pyplot as plt

# 離散化などの前処理（詳細はリポジトリ参照）
# ...

# 構造学習の実行
hc = HillClimbSearch(df_discrete)
best_model = hc.estimate(scoring_method=BicScore(df_discrete))

# グラフ描画
G = nx.DiGraph()
G.add_edges_from(best_model.edges())
# ... (描画コード)

結果

出力されたグラフがこちらです。

見事な 『条件付き独立』 の構造が現れました！ （※理論的には共通原因を示す『ハの字（Fork）』になるはずですが、今回はマルコフ等価性により一部の矢印が連鎖（Chain）の形になっています。しかし『直接の因果はない』という結論は変わりません）

Temperature \to Wind_Speed

Barrel_Sales \to Temperature

Wind_Speed と Barrel_Sales の間には線がない

アルゴリズムは、データの中に潜む確率的独立性を計算し、「気温さえ分かれば、風と売上は無関係（条件付き独立）」 であることを見つけ出したのです。

考察・まとめ

今回の検証で、以下のことが確認できました。

相関 \neq 因果:

直接的な関係がなくても、共通の親がいれば強い相関が出る。

構造の重要性:

ベイズネットワーク等を用いることで、データの背後にある「生成プロセス」をある程度推定できる。発展的なアプローチについて今回はデモとしてシンプルな離散化アプローチをとりましたが、実際の現場（連続値データ）で探索的データ解析を行う場合は、以下のような手法が有効です。

LiNGAM:

連続値をそのまま扱い、非ガウス性を利用して因果の向きを一意に特定する手法。

なお、実行結果によっては『売上 \to 気温』という、物理的にありえない逆向きの矢印が出ることがあります。
これは、統計的には『A と B の相関』は対称であり、データだけからは矢印の向き（因果の方向）を特定できないケースがあるためです（マルコフ等価性）。
だからこそ、『売上で天気は変わらない』という人間のドメイン知識（ブラックリスト）をアルゴリズムに与えることが、実務では不可欠なのです。

ドメイン知識の注入:

「売上が天気を変えることはない」といった物理的制約をブラックリストとして与える。データ分析においては、目の前の数値（相関）だけでなく、その背後にある 構造（因果） を意識することが、正しい意思決定への第一歩だと感じました。

人間（データサイエンティスト）は因果の裁判官

AI に思考停止で答えを求めるのは愚かだが、『人間が思いつきもしない相関（仮説）の種』を AI に見つけてもらい、それを人間が因果推論というナイフで解剖する。この共生関係こそが、これからのデータサイエンスの形なのかもしれないですね。

GitHubで編集を提案

Discussion