⛳

動的計画法のまとめ

2023/07/02に公開

この記事について

こちらは、動的計画法の簡単なまとめになります。

動的計画法の基礎

動的計画法とは

動的計画法（Dynamic Programming）は、複雑な問題をよりシンプルな部分問題に分割し、それぞれの部分問題の解を再利用することで全体の解を求めるアルゴリズムです。

動的計画法は、再帰呼び出しやループを使って、問題を小さな部分問題に分解します。また、部分問題の解をメモしておくことで、同じ部分問題が複数回計算されることを避けることができます。

例えば、フィボナッチ数列の例を考えてみましょう。フィボナッチ数列は、前の2つの数の和が次の数になるという性質を持つ数列です。動的計画法を使ってフィボナッチ数列を計算する場合、再帰呼び出しやループを使って部分問題を計算し、メモしておくことで、同じ部分問題が複数回計算されないようにします。

メモ化再帰

メモ化再帰（Memoization）は、再帰的なアルゴリズムを使って動的計画法を実装する方法の一つです。メモ化再帰では、再帰呼び出しの結果をメモしておき、同じ引数での再帰呼び出しの結果を再計算せずに再利用します。

具体的なコード例を見てみましょう。以下は、フィボナッチ数列をメモ化再帰を使って計算するPythonのコードです。

memo = {}

def fibonacci(n):
    if n in memo:
        return memo[n]
    if n <= 1:
        result = n
    else:
        result = fibonacci(n - 1) + fibonacci(n - 2)
    memo[n] = result
    return result

# フィボナッチ数列の5番目を求める例
print(fibonacci(5))  # 結果: 5

このコードでは、フィボナッチ数列の各要素を計算するたびに、その結果をmemoという辞書にメモしています。次に同じ要素を計算する必要がある場合は、メモから結果を取得して再利用します。

ナップサック問題

ナップサック問題の概要

ナップサック問題（Knapsack Problem）は、与えられた制限付きの容量を持つナップサックに、価値や重みの異なるアイテムを詰め込む際の最適な組み合わせを求める問題です。

具体的な例として、容量が10のナップサックに、価値が6のアイテムAと価値が8のアイテムBがあります。アイテムの重さがそれぞれ4と6である場合、この問題ではどのアイテムを選ぶべきかが求められます。

ナップサック問題の解法

ナップサック問題は、動的計画法を用いて解くことができます。以下のような手順で解を求めることができます。

ナップサックの容量とアイテムの数を定義します。
動的計画法のテーブル（配列）を用意し、初期値を設定します。
テーブルを更新していきます。
最終的な結果をテーブルから読み取り、最適な組み合わせが得られます。

具体的な実装例を見てみましょう。以下は、ナップサック問題を動的計画法を使って解くPythonのコードです。

def knapsack_problem(capacity, weights, values):
    n = len(weights)
    dp = [[0] * (capacity + 1) for _ in range(n + 1)]
    
    for i in range(1, n + 1):
        for j in range(1, capacity + 1):
            if j >= weights[i - 1]:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])
            else:
                dp[i][j] = dp[i - 1][j]
    
    return dp[n][capacity]

# ナップサックの容量が10で、アイテムAの重さが4、価値が6、アイテムBの重さが6、価値が8の場合
weights = [4, 6]
values = [6, 8]
capacity = 10

print(knapsack_problem(capacity, weights, values))  # 結果: 8

このコードでは、ナップサックの容量とアイテムの数に対応する二次元配列dpを用意し、動的計画法のテーブルとして利用しています。テーブルの各セルには、その位置までのアイテムを考慮した場合の最大の価値が格納されます。

最長共通部分列

最長共通部分列の概要

最長共通部分列（Longest Common Subsequence）は、2つのシーケンス（文字列や配列など）において、一方のシーケンスからいくつかの要素を削除して、他方のシーケンスにするために必要な要素の最大数を求める問題です。

最長共通部分列は、文字列処理やバイオインフォマティクスなどの分野で広く使われる問題です。例えば、2つの文字列 "ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" と "GTCGTTCGGAATGCCGTTGCTCTGTAAA" の最長共通部分列は "GTCGTCGGAAGCCGGCCGAA" です。

最長共通部分列の解法

最長共通部分列は、動的計画法を使って解くことができます。以下のような手順で解を求めることができます。

2つのシーケンスの長さを取得します。
動的計画法のテーブル（配列）を用意し、初期値を設定します。
テーブルを更新していきます。
最終的な結果をテーブルから読み取り、最長共通部分列が得られます。

具体的な実装例を見てみましょう。以下は、最長共通部分列を動的計画法を使って解くPythonのコードです。

def longest_common_subsequence(text1, text2):
    m, n = len(text1), len(text2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if text1[i - 1] == text2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
    
    return dp[m][n]

# 2つの文字列 "ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" と "GTCGTTCGGAATGCCGTTGCTCTGTAAA" の最長共通部分列を求める例
text1 = "ACCGGTCGAGTGCGCGGAAGCCGGCCGAA"
text2 = "GTCGTTCGGAATGCCGTTGCTCTGTAAA"

print(longest_common_subsequence(text1, text2))  # 結果: 20

このコードでは、2つの文字列の各文字を比較し、動的計画法のテーブルの各セルに最長共通部分列の長さを格納しています。テーブルの位置 (i, j) には、テキスト1の最初のi文字とテキスト2の最初のj文字までを考慮した場合の最長共通部分列の長さが格納されます。

最長増加部分列

最長増加部分列の概要

最長増加部分列（Longest Increasing Subsequence）は、与えられた数列の中で、隣り合う要素よりも大きい部分列の最大の長さを求める問題です。

最長増加部分列は、データの並び替えや最適化などの問題に応用されます。例えば、数列 [10, 9, 2, 5, 3, 7, 101, 18] の最長増加部分列は [2, 5, 7, 18] です。

最長増加部分列の解法

最長増加部分列は、動的計画法を使って解くことができます。以下のような手順で解を求めることができます。

数列の長さを取得します。
動的計画法のテーブル（配列）を用意し、初期値を設定します。
テーブルを更新していきます。
最終的な結果をテーブルから読み取り、最長増加部分列の長さが得られます。

具体的な実装例を見てみましょう。以下は、最長増加部分列を動的計画法を使って解くPythonのコードです。

def longest_increasing_subsequence(nums):
    n = len(nums)
    dp = [1] * n
    
    for i in range(1, n):
        for j in range(i):
            if nums[i] > nums[j]:
                dp[i] = max(dp[i], dp[j] + 1)
    
    return max(dp)

# 数列 [10, 9, 2, 5, 3, 7, 101, 18] の最長増加部分列を求める例
nums = [10, 9, 2, 5, 3, 7, 101, 18]

print(longest_increasing_subsequence(nums))  # 結果: 4

このコードでは、数列の各要素を比較し、動的計画法のテーブルの各セルに最長増加部分列の長さを格納しています。テーブルの位置 i には、数列の最初のi個の要素までを考慮した場合の最長増加部分列の長さが格納されます。

フィボナッチ数列

フィボナッチ数列の概要

フィボナッチ数列（Fibonacci sequence）は、前の2つの数の和が次の数になる数列です。例えば、0, 1, 1, 2, 3, 5, 8, 13, ... のような数列がフィボナッチ数列です。

フィボナッチ数列は、数理やコンピュータサイエンスなどの分野で広く使われます。例えば、フィボナッチ数列は、金融工学のオプション価格計算や、アルゴリズムの効率を評価するためのベンチマークテストにも利用されます。

フィボナッチ数列の解法

フィボナッチ数列は、動的計画法や再帰呼び出しなど、複数の方法で計算することができます。以下は、フィボナッチ数列を再帰呼び出しを使って計算するPythonのコードです。

def fibonacci(n):
    if n <= 1:
        return n
    return fibonacci(n - 1) + fibonacci(n - 2)

# フィボナッチ数列の5番目を求める例
print(fibonacci(5))  # 結果: 5

この再帰呼び出しの方法は、シンプルで理解しやすいですが、重複した計算が多く行われるため、効率が良いとは言えません。そこで、メモ化再帰（先ほどの動的計画法の基礎で説明した手法）を使うことで、重複した計算を避けることができます。

memo = {}

def fibonacci(n):
    if n in memo:
        return memo[n]
    if n <= 1:
        result = n
    else:
        result = fibonacci(n - 1) + fibonacci(n - 2)
    memo[n] = result
    return result

# フィボナッチ数列の5番目を求める例
print(fibonacci(5))  # 結果: 5

このメモ化再帰の実装では、計算結果をmemoという辞書にメモしておくことで、同じ引数に対して再帰呼び出しを行った場合には、結果を取り出して再計算せずに済むようになります。

動的計画法の応用

グラフ問題への応用

動的計画法は、グラフ問題にも広く応用されます。グラフ問題では、頂点や辺の組み合わせを効率的に探索したり、最短経路や最小コストなどの問題を解くことが求められます。

例えば、最短経路問題では、あるスタート地点からゴール地点までの最短経路を求める問題です。動的計画法は、最短経路問題にも応用され、頂点間のコストを表すテーブルを更新しながら最適解を求めることができます。

文字列処理問題への応用

動的計画法は、文字列処理問題にも応用されます。文字列処理問題では、与えられた文字列に対して、部分文字列の検索や操作を行う問題が求められます。

例えば、最長共通部分列問題や最長増加部分列問題は、文字列処理問題の一部です。動的計画法を使うことで、文字列の特定の性質やパターンを効率的に求めることができます。

これらの問題において、文字列を部分文字列に分割したり、文字列の一部を操作したりすることで、部分問題を解き、問題全体の解を求めることができます。

実はこの記事………

ここまで読んで頂き、ありがとうございます。

実はこの記事、開発中の「チュートリアルMaker」というアプリで作成しています。

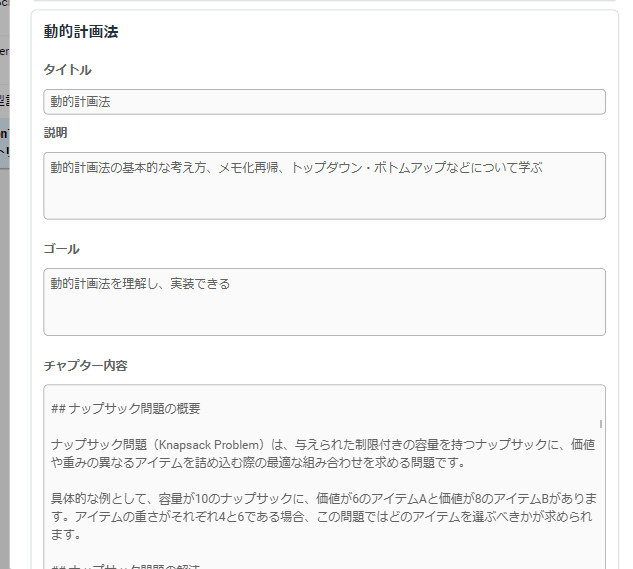
チュートリアルMakerでは長文のチュートリアルを簡易的な文章から作成することが可能です。

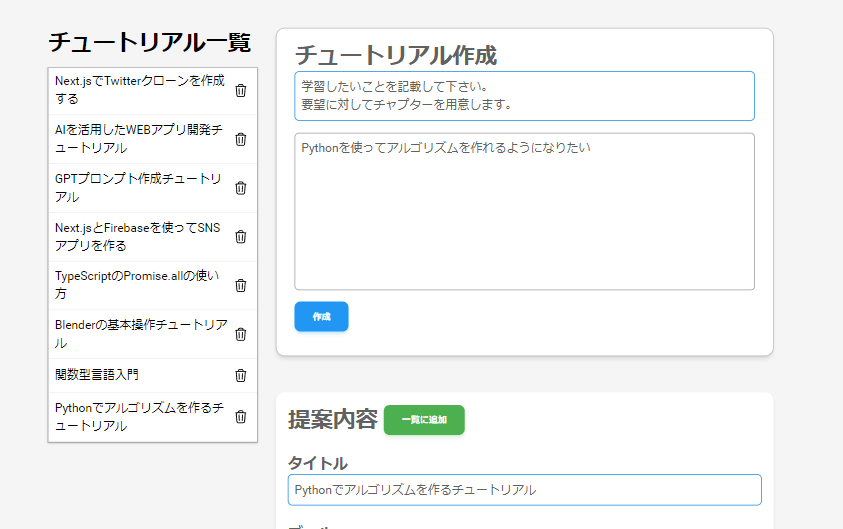
以下は、実際に作成してくれる画面の一部になります。

この記事の目的

そもそもなぜこの記事を書いたのか？

それは、内容検証のためです。

現在、チュートリアルMakerでは複数の問題点があり、そのうちの一つが「長文が書けない」という問題点です。

この記事を読んでいただいた方は「長かったような？」とお気づきの方もおられると思いますが、確かにこの記事は5000文字程度の中文になっており、そこそこ長いです。

色々と試行錯誤した結果、初期の段階の1000文字から5000文字にできたわけですが、それと同時に「意味通じてる？」という問題点が発生しました。

そこで私一人の感覚では分からないため、今回は冒頭でネタ明かしをせずに文章を掲載し、純粋な状態で内容を読んだ方が理解できるかを検証しようと、この記事を掲載させていただきました。

ただ、この機能を使って記事を量産してしまうと検索を汚染してしまう恐れがあるため、検証はこの程度でとどめようと思います。

もし今回の記事の意味が分かるようでしたら、是非とも「いいね」頂けると幸いです。

宜しくお願い致します。

チュートリアルMakerについて（宣伝）

ここからは宣伝です。

チュートリアルMakerは学びたい事柄を入力すると、それに沿ってチュートリアルを作成してくれるアプリです。

今まで、記事作成において「大量の文章を書けない」や「長いチュートリアルを書くと話がつながらない」といった問題点があったと思います。

チュートリアルMakerでは、そういった課題を解決すべく、色々と頑張っています。

近日中にデモ版を公開予定ですので、もしよろしければ、フォローのほどよろしくお願いいたします。