CORDICアルゴリズムを導き出す

（この記事は、2016年1月に筆者の別ブログで公開したものです）

CORDICアルゴリズムは組み込み系の数値計算に携わっていると随所でその名を見かけます。

むろん、ワークステーション系の恵まれた環境であれば全てはライブラリ化されており、こんなものにはお目に掛かりません。CORDICの名が浮上するのは手厚い支援を受けられない組み込みならではの事と言えます。

CORDICアルゴリズムは「実装が簡単でプログラムも単純である」というのがうたい文句ではあるのですが、一方でCORDICアルゴリズムが正しく動作する理由は、プログラムを子細に読んでもわかりません。ある意味、FFTと同じくらい元の数学から乖離した手順を踏んでいると言ってよいでしょう。

以下では数学的背景から順を追って説明し、三角関数のCORDICアルゴリズムを導き出します。是非、このアルゴリズムが導き出される巧妙な過程を楽しんでください。

CORDICアルゴリズムの導出

複素平面と回転子

最初に複素平面の事を考えてみましょう。CORDICアルゴリズムは平面上の線形な変形操作（アフィン変換）を利用したアルゴリズムです。ですので平面から話を始める方がすっきりするというものです。

よく使う複素平面は図1のように、横軸に実部、縦軸に虚部を配置したものです。図1はさらにこの平面の上に、点$(1,0)$を基点とし、$(0,0)$を回転中心としてコンパスを使って半径1の円弧を書き込んだものです。このとき、$(0,0)$から実軸に対して角$θ$の直線を定規で引いて円弧と交わる点$P$を作図します。このとき、その点$P$の座標が$(cos(\theta), sin(\theta))$です。

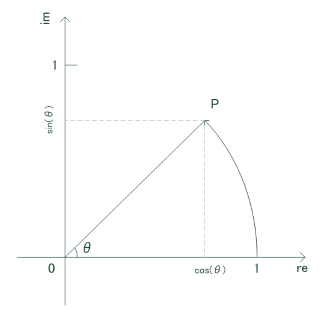
図1: 複素平面と点$P$の作図

次に少し視点をひねってみましょう。この図をながめるとき、我々は上に書いたようにコンパスと定規による作図を想定しました。しかし上の図は、実軸上の点$(1,0)$を、回転によって点$P$まで移動させる操作と考えることもできます。その場合、操作はコンパスと定規による作図ではなく、数式による計算ということになります。

さて、上の座標は複素平面ですので点$(1,0)$は、複素数で$1+0i$と表すことができます。そしてこれをPまで移動させるには、次のような演算を行います。

$$\tag{1} (1+0i)(cos\theta+i\,sin\theta)=cos\theta+i\,sin\theta$$

ここで、$cosθ+i\,sinθ$は、複素平面上の点を原点を中心に角$θ$だけ反時計回りに回転させる複素回転子です。

このように、複素数一つを掛けることで、複素平面上の任意の点を好きな角度だけ原点を中心に回転させてその座標を計算することができます。

回転子群からsin(x)とcos(x)を求める

与えられた$x$に対して、$sin(x)$と$cos(x)$を求めるにはどうすればいいでしょうか。

一つには級数展開した$sin(x)$、$cos(x)$を真面目に計算していく方法が考えられます。もう一つ考えられるのは既知の複素回転子を使用して$x$に等しい角の回転を合成する方法です。例えば次のような表を考えてください。

表1: 回転子

インデックス	$\theta$	$cos(\theta)$	$sin(\theta)$	回転子
$0$	$45$	$0.707$	$0.707$	$0.707+0.707i$
$1$	$22.5$	$0.924$	$0.383$	$0.924+0.383i$
$2$	$11.25$	$0.981$	$0.195$	$0.981+0.195i$

表のように、角が45度、22.5度、11.25度…と次々に1/2になっていく回転子の表をあらかじめ持っているとしましょう（$θ$と回転子だけでいい）このような場合、表中の回転子を組み合わせて適用することで、与えられた$x$に最も近い$x'$を作り出しすことができます。

例えば、$x$が66.5度だとしましょう。この場合、$45+22.5=66.5$ですので、$(1,0)$を回転させたときの$P$の座標は

$$\tag{2} (1+0i)(0.707+0.707i)(0.924+0.383i)$$

を計算すれば求めることができます。すなわち$θ=65$度のときの$P$の座標が計算で分かります。これは図2のようになります。

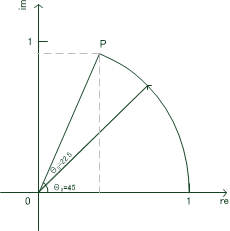
図2: 回転子を用いたsin(x)とcos(x)の計算

図2で分かるように、この場合の回転子は二つの回転子の合成ですが、考え方を変えると、「まず45度動かして、つぎに22度動かしている」ともとれます。その場合、点の座標を表す複素数に対して次々に回転子である複素数を掛けていくことになります。

これらをまとめて一般化してみましょう。点$(p,q)$に対する1回の回転演算は次のようになります。

$$\tag{3} (p+q\,i)(r+s\,i)=(pr–qs)+(ps+qr)i$$

ここで$(r+s\,i)$は回転子の複素数表現です。

右辺を見てわかるように、1回の複素乗算あたり4回の実数乗算が必要になります。これを、$θ$の誤差が十分小さくなるまで先の表の各行の回転子を使って繰り返していけば、与えられた$x$に対する十分精度の高い$sin(x)$、$cos(x)$を求めることができます。

スケーリングして乗算を減らす

複素平面上で既知の角度の回転を繰り返していくことで、与えられた角$x$に対して十分精度の高い$sin(x)$$とsin(x)$を求めることができます。しかしながら、1回の繰り返しあたり4回の実数乗算では演算コストが大きすぎます。そこで、これを削ってみましょう。

削るための方法はスケーリングです。先に挙げた$θ$と回転子の表を元に、回転子にスケーリング･ファクタ$S$を掛けることにします。ここで$S$は$1/cosθ$です。そうすると、以下のように修正回転子の表をえることができます。

表2: スケーリングを導入する

インデックス	$\theta$	回転子	$S$	修正回転子
$0$	$45$	$0.707+0.707i$	$1/0.707$	$1+1i$
$1$	$22.5$	$0.924+0.383i$	$1/0.924$	$1+0.414i$
$2$	$11.25$	$0.981+0.195i$	$1/0.981$	$1+0.198i$

修正回転子は、スケーリングによって実部が1に固定されています。その結果、上の式3は修正回転子によって次のように変形されます。

$$\tag{4} \frac {(p+qi)(1+si)} {S} = \frac{(p–qs) + (ps+q)i } {S}$$

$S$による除算が増えています！しかし、ここでは一旦そこから目をそらしましょう。そうすると、乗算の数は4から2に減っていることがわかります。$S$による除算については後でもう一度考えます。

この変形を座標上で考えてみましょう。式4からあえて$S$による補正を取り除くと、座標上での点の動きは図3のようになります。これまで綺麗な円弧を描いていた回転子は、スケーリングによって三角形に置き換わっています。修正回転子は実部が常に1であり、点$(1,0)$と回転した点と原点で三角形を作ると、必ず直角三角形になります。

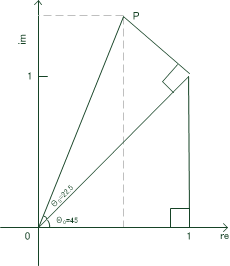
図3: スケーリングによる三角形の生成

そして、図3を見れば一目瞭然ですが、原点から$P$へのベクトルの長さは修正回転子を適用する度に長くなっていきます。それがスケーリングの副作用であり、$S$による補正が必要な理由です。

三角形の高さを1/(2^n)にして乗算を減らす

スケーリング･ファクタの導入で乗算を減らすことができました。これをさらに減らしてみましょう。

表2で、修正回転子の虚部は1,0.414,0.198となっています。これを思い切って、1, 0.5, 0.25 … 1/2^nに変更するとどうなるでしょうか。

表3: 回転子の虚部を1/(2^n)にする

インデックス	$θ$	$S$	修正回転子2
$0$	$45$	$1.414$	$1+1i$
$1$	$26.6$	$1.118$	$1+0.5i$
$2$	$14.0$	$1.031$	$1+0.25i$
$n$	$atan(\frac 1 {2^n})$	$\sqrt{1+\frac 1 {2^{2n}}}$	$1+\frac 1 {2^n}i$

こうすると、上の回転の式4は次のようになります。

$$\tag{5} (p+q\,i)(1+\frac 1 {2^n}i) = \frac {(p–q\frac 1 {2^n})+(p \frac 1 {2^n} + q )i } {S}$$

なにやら却って複雑になったように思えますが、ここで思い直してみましょう。$\frac 1 {2^n}$はnビットの右シフト演算です。

$$\tag{6} (p+q\,i)(1+\frac 1 {2^n}i) = \frac {(p–q \gg n)+(p \gg n + q )i } {S}$$

つまり、ここまでの変形によって、繰り返し1回あたり乗算4つの演算だったのが、加減算とシフト演算（およびスケーリング処理）にまで演算負荷を下げることができました。

折りたたんでスケーリングを解決する

「与えられた角$x$と同じ角度を、あらかじめ角が分かっている回転子の組み合わせで合成する」という考え方で、複素座標上での点を動かすことをこれまで考えてきました。

ここまでの手順の変形により、点$P$を位置$(1,0)$から始めて既知の回転子を適用していくことにより、与えられた角$x$に近づけていくことができます。回転子の適用1回当たり乗算が4回必要ですが、スケーリング・ファクタの導入と、虚部の変形によって乗算4回は加減算とシフト演算だけになりました。ただし、スケーリング･ファクタを最後に取り除く必要があります。

スケーリング･ファクタの取り除きに必要な演算はどのくらいになるでしょうか。これを見積もることは簡単です。角$x$を作り出す（あるいは最も近い角を作り出す）ために$k$個の回転子が必要な場合、必要な補正演算は次のようになります。

• $k$個の回転子それぞれのスケーリング・ファクタを取り出して、それら全ての積を求める
• 求めた積の逆数を求める

つまり、乗算$k-1$回と除算1回になりました。元々は乗算$4k$回でしたからこれでも随分軽くなりましたが、ここはもう一声がんばってみましょう。

これまでの方法では、表の中から必要な回転子だけを選び出して与えられた角xを合成していました。これをやめて表にある回転子全部を使用することにします。

例えば、表3のインデックスが0から14までの計15個であれば、15個の回転子全部を使うことにします。一見無駄に見えるこの方法のメリットはSによる補正値の計算を事前に済ませる事ができる点です。なにしろ回転子は全部使います。ですから、コーディング時に全ての$S$の積とその逆数を計算しておけばいいのです。これで、演算中の$S$の補正は乗算1回ですむようになりました。

そして、もう一度頭をひねることで、そもそも$S$の補正を実行中に行う必要は無いことに気がつきます。回転を始める点の初期値を$(1,0)$ではなく、$(\frac 1 {S_{ALL}}, 0)$とすればいいのです。ここで$S_{ALL}$は全ての$S$の積であり、$S_{ALL}=\prod S_n$です。

一方、全ての回転子をつかって反時計回りに回転を行えば、求める角$x$を追い越してしまうことは自明です。そこで、次のような方策を採ります。

• インデックス0から始める
• 合成した角がxより小さければ、次の回転子をつかって反時計回りに回転させる。
• 合成した角がxより大きければ、次の回転子をつかって時計回りに回転させる。
• これを全てのインデックスに昇順に適用する

この方法を使うと、回転による点の動きは図3のように折り返しを含むものになります。

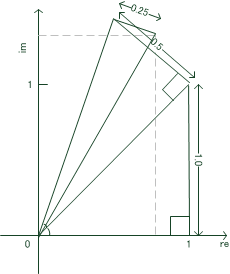
図4: 折り返しを含む回転

今回は時計回りの回転が入ってきます。その場合は(式6)を書き換えて次の式で時計回りの回転を求めることができます。

$$\tag{7} (p+q\,i)(1-\frac 1 {2^n}i) = \frac {(p+q \gg n)+(-p \gg n + q )i } {S}$$

sin(x)、cos(x)を求めるCORDICアルゴリズム

以上の考察を元に導き出されたCORDICアルゴリズムはおおむね以下のようになります。

function sincos( x )
    p = 1/S_ALL
    q = 0
    angle = 0

    for ( i = 0; i< MAXINDEX; i++ )

        if x > angle
            // 反時計回り
            p_next = p – q >> i
            q_next = q + p >> i
            angle += theta[i]
        else
            // 時計回り            
            p_next = p + q >> i
            q_next = q – p >> i
            angle -= theta[i]
        end if

        p = p_next
        q = q_next
    end for

    cos = p
    sin = q
    return( sin, cos )
end function

よく言われているとおり、乗除算を用いずに加減算とシフト演算のみで$sin(x)$, $cos(x)$を求めることができます。

収束するのか？

さて、こうしてCORDICアルゴリズムを求めることができました。求めたアルゴリズムは乗算を含まず、加減算とシフト演算だけで実装できます。また事前に必要な定数も1/S_ALLと、theta[n]だけで、非常にコンパクトです。

しかし、そもそもこのアルゴリズムは収束するのでしょうか。

ポイントは与えられた$x$に対して十分近いthetaを合成できるか否かです。thetaさえ合成できれば回転アルゴリズムには問題ありません。従って、「CORDICアルゴリズムは収束するのか」という問いは、「$x$に十分近いangleを常に合成できるか」という問いに変換できます。

表1に基づく回転だけを用いるのであれば、直感的にこのアルゴリズムは収束すると言えます。コンピュータ技術者であれば、2の巾乗だけを足し合わせて任意の整数を作ることができると知っています。二進数の基本です。

しかし、乗算を削るために導き出した表3は、$θ$の数列が等比数列になっていません。従って、収束するかどうかは自明ではありません。

詳しい考察はめんどくさいのでしていませんが、直感的に「任意のtheta[k]を選んだときに、theta[k+1]からtheta[n]の総和がtheta[k]より大きければ、xに十分近いangleを合成できる」と言えるようです。

なんにせよ、世間では広くCORDICアルゴリズムが使われています。精度に関して言えば、N回繰り返しを行うCORDICアルゴリズムは、Nが大きな領域ではNを1増やす毎にアルゴリズム固有の雑音が1/2になっていきます。

atan2(x,y)

ここまで、与えられた角$x$から$sin(x)$,$cos(x)$を求めるCORDICアルゴリズムについて解説しました。

では、与えられた座標$(X,Y)$から角$x$を求めるアルゴリズムはどうでしょうか。

結論からいえば、$sin(x)$,$cos(x)$を求めるアルゴリズムをほんの少し修正すればそれで実現できます。ポイントとなるのは、ループの中のif文の条件式です。

sin,cosを求めるときには「合成したangleがxより大きいか否か」を判別して回転方向を決めています。atan2(X,Y)アルゴリズムでは、ここを「qの値が正か負か」で判別するようにします。回転を重ねてqを0に近づくように追い込んでいけば、ループから出たときには-atan2(Y,X)の値がangleに格納されています。

function atan2( x, y )
    p = x
    q = y
    angle = 0

    for ( i = 0; i< MAXINDEX; i++ )

        if p < 0    // pが負ならば
            // 反時計回り
            p_next = p – q >> i
            q_next = q + p >> i
            angle += theta[i]
        else
            // 時計回り
            p_next = p + q >> i
            q_next = q – p >> i
            angle -= theta[i]
        end if

        p = p_next
        q = q_next
    end for

    // angleには-atan2(y,x)が格納されている
    return( -angle )
end function

終わりに

CORDICアルゴリズムについて解説しました。

このアルゴリズムは実装が容易で必要な資源も軽いことで有名です。しかし、それを導き出す過程は最適化という観点から見たときに非常に興味深いものです。信号処理の最適化では時たまアルゴリズムから数学まで引き返して最適化を行う必要がありますが、CORDICはその好例と言えるでしょう。