Zenn
🧠

誰でもわかる Deep Learning 入門

2021/08/29に公開
AI
ディープラーニング
機械学習
#
深層学習
tech

はじめに

「Deep Learning」（ディープ ラーニング）についての解説です。
「ヒトみたいなことができるらしいけど、一体どんな仕組みになってるの？」と思われている方に、仕組みをざっくりご理解いただくことが目的です。

ソフトウェア エンジニアではない方や学生の方でも分かるよう、なるべく専門用語を排除してみました。途中に少しだけ数式やプログラムらしきものも出てきますが、適当に読み飛ばしていただいて大丈夫です。

なお、2021年8月26日に Easy Easy というエンジニア コミュニティ主催のオンライン イベントでお話した内容とほぼ同じなので、その時のスライドも置いておきます。

1.脳

脳のすごいところ

突然ですが、ヒトの脳はすごいです。

  • 計算できる
  • 読める・書ける
  • しゃべれる
  • 絵だって描ける
  • 知識や経験で判断できる
  • 将来の予想もできる
  • 経験や訓練で効率が上がる
  • できることが勉強で増やせる

当たり前のように思われるかもしれませんが、コンピューターではこうはいきません。できることを増やすにはプログラムの追加や修正が必要です。

脳は産まれた時にできた1つの仕組みで、経験や訓練をすれば性能が上がり、勉強すればできることが増やせます。これはすごいことなのです。

脳の仕組み

脳は、神経細胞と呼ばれる特殊な細胞がつながりあってできています。下の図の黄色い部分が1つの細胞です。

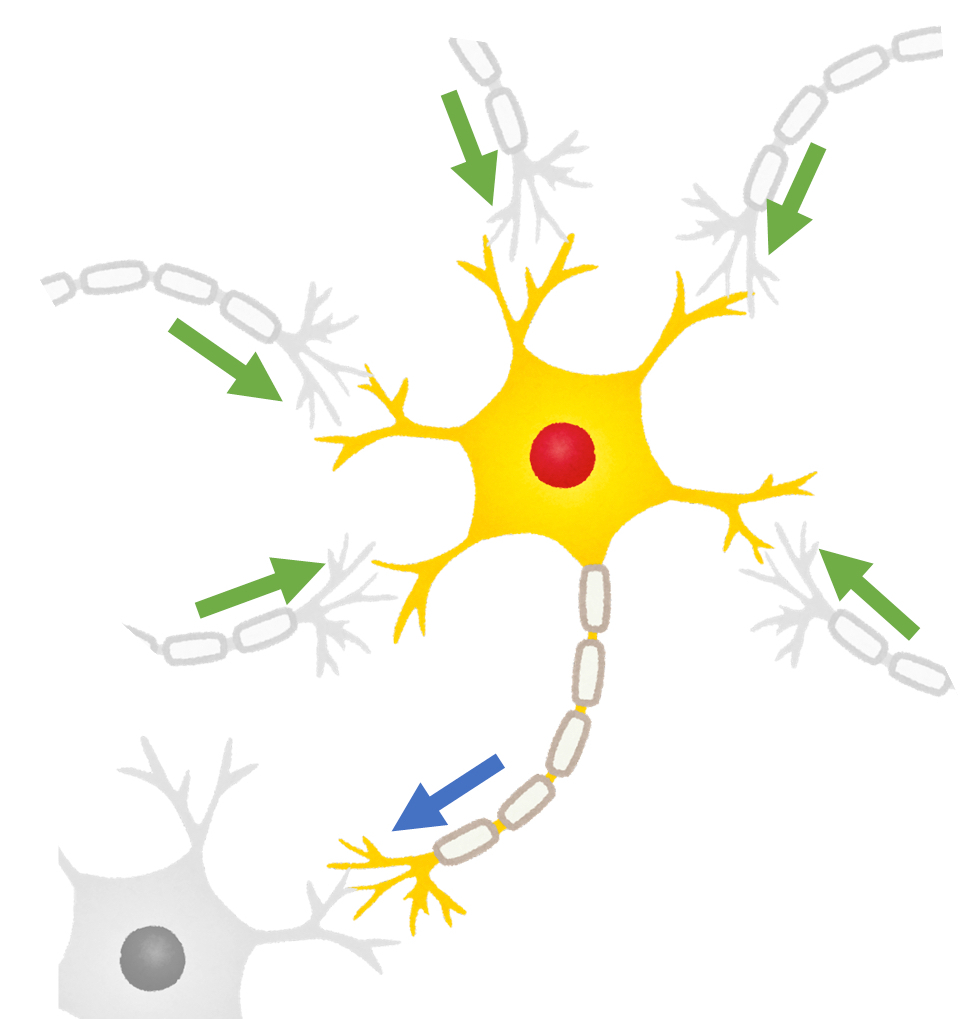
細胞は他の複数の細胞から信号を受け取ります。この図では、他の5つの細胞から緑の矢印の方向で信号を受け取っています。信号を受け取った細胞は、その強さの合計がある境界を越えると、次の細胞へ信号を伝えます。青い矢印がそれを示しています。

細胞間の信号の伝わりやすさや、次の細胞へ信号を伝えるかどうかの判断の境界は、細胞によってまちまちです。

脳をマネしたら？

1943年に神経生理学者・外科医のマカロックさんと論理学者・数学者のピッツさんがタッグを組み、脳の神経細胞をコンピューターでマネした仕組みを考えました。脳の仕組みを調べてコンピューターでマネすれば、ヒトと同じように思考できるAIが完成するはず！そんな奇想天外なアプローチです。

ここで考案された仕組みは非常にシンプルです。

下の図の中央の青の丸が1つの細胞です。左側の2つの細胞から信号を受け取りますが、途中の緑の線で伝わりやすさの影響を受けて、伝わる信号の強さが変化します。それらを受け取った青の細胞は、受け取った信号の合計が境界を越えたら次の細胞に信号を伝え、越えない場合は何もしません。

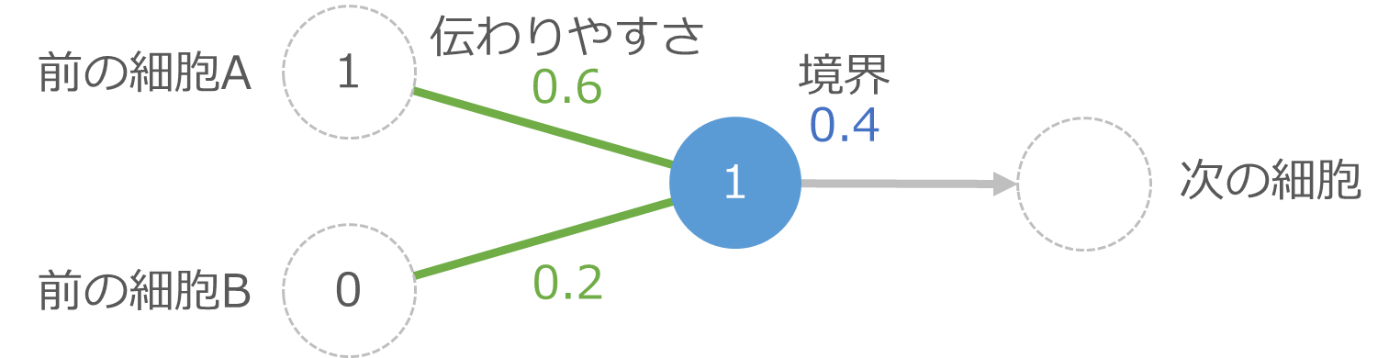
たとえば前の細胞Aから強さ 1 の信号が伝えられ、細胞Bからは強さ 0 の信号（つまり信号は伝えられなかった）とします。この時、上の図では細胞Aからの伝わりやすさは 0.6 なので、実際に伝わる信号の強さは 1×0.6 で 0.6 です。細胞Bからは信号がないので計算不要ですが、もし計算するのであれば 0×0.2 で 0 の信号が伝わった形です。

青い細胞は細胞Aから 0.6 、細胞Bから 0 の信号を受け取るので、信号の合計は 0.6 です。これは青い細胞の境界である 0.4 以上なので、次の細胞に強さ 1 の信号を伝えます。もし境界より小さい場合は次の細胞へは信号を伝えません。

これをプログラムで書くと次のような感じになります。

if (1 * 0.6 + 0 * 0.2 >= 0.4):
	出力 = 1
else:
	出力 = 0

1個の細胞でいろいろできる

脳をマネしたこの小さなプログラムは、かなりいろいろなことができます。
たとえば、伝わりやすさと境界をうまく調整すると、論理演算と呼ばれる計算の中の AND と OR と NAND の機能が1つの細胞で実現できてしまいます。

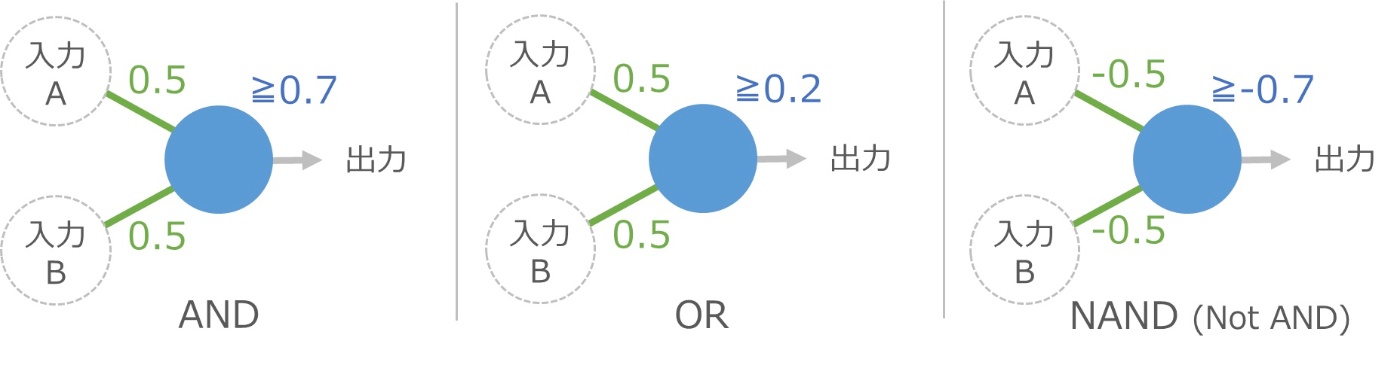
AND とは、両方の入力が 1 なら出力は 1 、それ以外は 0 という計算です。上の図で入力AとBが 1 の場合、青い細胞には 1×0.5+1×0.5 で合計 1 の信号が伝わり、境界の 0.7 以上なので出力が 1 になります。もし細胞Bが 0 の場合は、1×0.5+0×0.5 で合計 0.5 となり、境界に届かないので出力は 0 です。

OR は、どちらかが 1 なら出力も 1 になる計算です。同じ感じで計算できますね。

NAND は AND の逆の結果を返します。これは少し特殊で、右上のように伝わりやすさと境界にマイナスの値を使うと実現できます。伝わりやすさがマイナスというのはちょっと違和感がありますが、細かいことは気にしないで進みましょう。

ここで重要なのは、次のような1つのプログラムで、■の変数を変えるだけで3つの機能が実現できてしまうことです。これまで、機能を追加するにはプログラムの追加や修正が必要だったのですが、プログラムの修正は必要ありません。

if (入力A * ■ + 入力B * ■ >= ■):
	出力 = 1
else:
	出力 = 0

あいまいな処理もできる

このプログラムでおもしろいのは、入力が多少あいまいでも大丈夫なことです。

たとえばキャンプに出発する条件が「明日と明後日の天気が晴れなら」だったとします。これをコンピューターに判断させる場合、明日と明後日が晴れかどうかを入力して AND を計算させる形になります。

ヒトなら明日の降水確率が10%で明後日の降水確率が20%でもキャンプに行くかと思いますが、コンピューターはこの辺の融通がなかなか効きません。AND を計算する時に、晴れる確率として 0.9 と 0.8 を渡して AND を計算させようとしても普通は計算できません。AND の計算は入力が 0 か 1 という前提があるためです。

ところが、今回の細胞をマネしたプログラムでは、入力に 0.9 と 0.8 を渡しても計算できます。

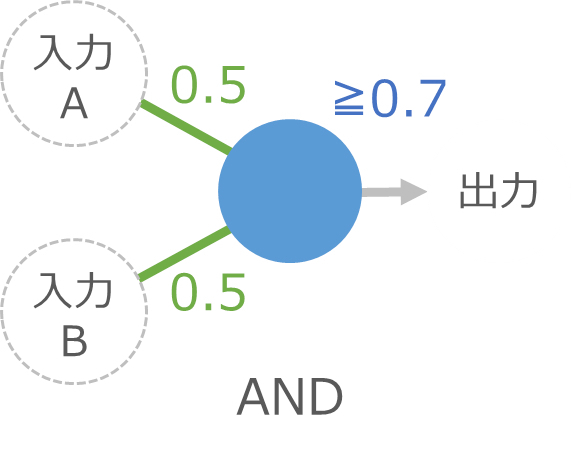
青い細胞への入力は 0.9×0.5 + 0.8×0.5 = 0.85 になって 0.7 以上なので、無事キャンプへ出発できます。このように、伝わりやすさや境界の変数の調整によって、あいまいなデータでも処理できるところがポイントです。

細胞が3個あると XOR もできる

細胞1つでは論理演算の XOR は計算できないのですが、細胞が3つあると実現できます。XOR はどちらかの入力が 1 なら出力が 1 、ただし両方 1 の場合は 0 になる計算です。

入力Aからは2つの青い細胞に信号が伝わります。入力Bからも同様です。それらを受け取った2つの細胞は、右の1つの青い細胞に出力を伝えます。このような2段階の計算を経て最後の出力が決まります。

実際に入力AとBに値を指定して計算してみると、XOR が実現できていることがわかります。

細胞が160個あると 手書き数字も認識できる

細胞を160個使って次のように組み合わせると、なんと手書きの数字が認識できてしまいます[1]。

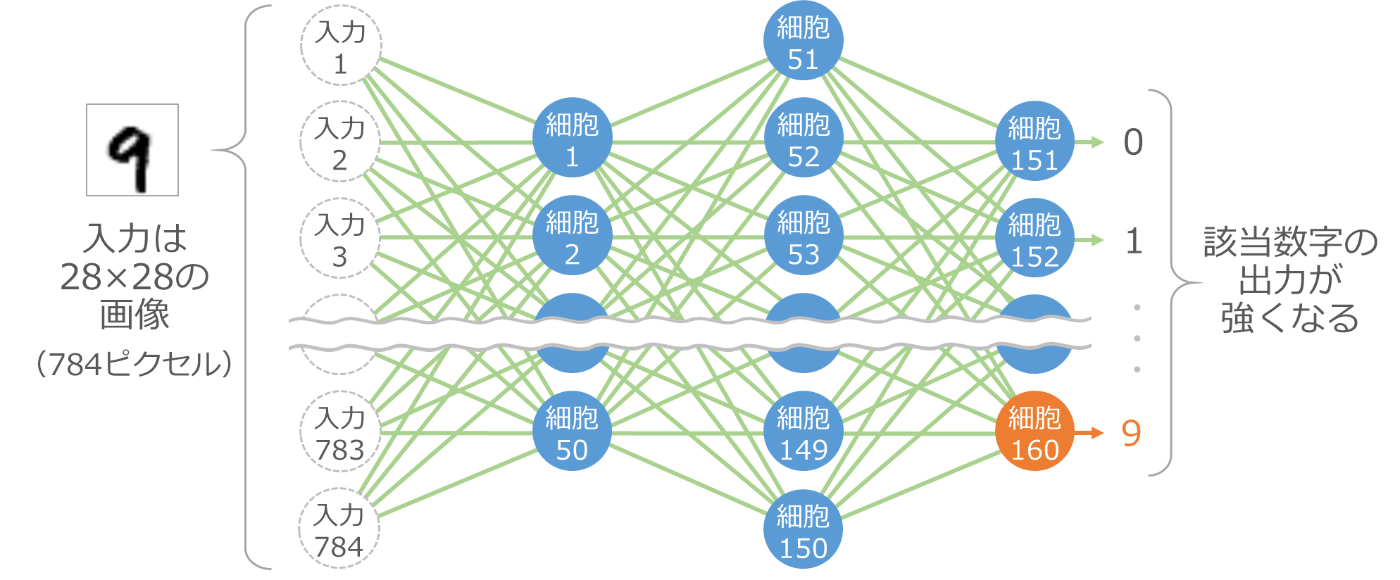
入力は 784個のデータで、縦横 28 ピクセルの画像データです。これを入力データとして、50個（細胞1から細胞50）の細胞の出力を計算します。次にこの50個の出力を入力として、次の100個（細胞51から細胞150）の出力を計算します。最後にこの100個の出力を入力として、最後の10個（細胞151から細胞160）の出力を計算します。

最後の10個の細胞は数字の 0 から 9 に対応しており、入力で渡した画像に対応する数字の細胞の出力が強くなる仕組みです。これにより、手書き数字の画像がどの数字なのかを認識できます。

ここまでのまとめ

  • 脳の神経細胞をマネすると、変数（細胞間の信号の伝わりやすさと次へ伝える境界）を変えるだけでできることが増やせます。
  • 細胞を増やせば、複雑なこともできるようになります。

ここで問題になるのは、変数をどうやって決めるのか？です。AND や OR くらいならまだ考えることができますが、細胞が3つになった XOR はかなり難しいですよね。手書き数字の認識みたいな話になると、とても考えられそうにありません。

どうやって変数を決めればよいのでしょうか。

2. 伝わりやすさと 境界の決め方

手書き数字の認識を例にご説明します。

とりあえず1か所だけ調整

まず、伝わりやすさや境界の変数の値を、適当にランダムな値にしておきます。そして、手書き数字の 0 の画像を1枚渡して出力を計算します。

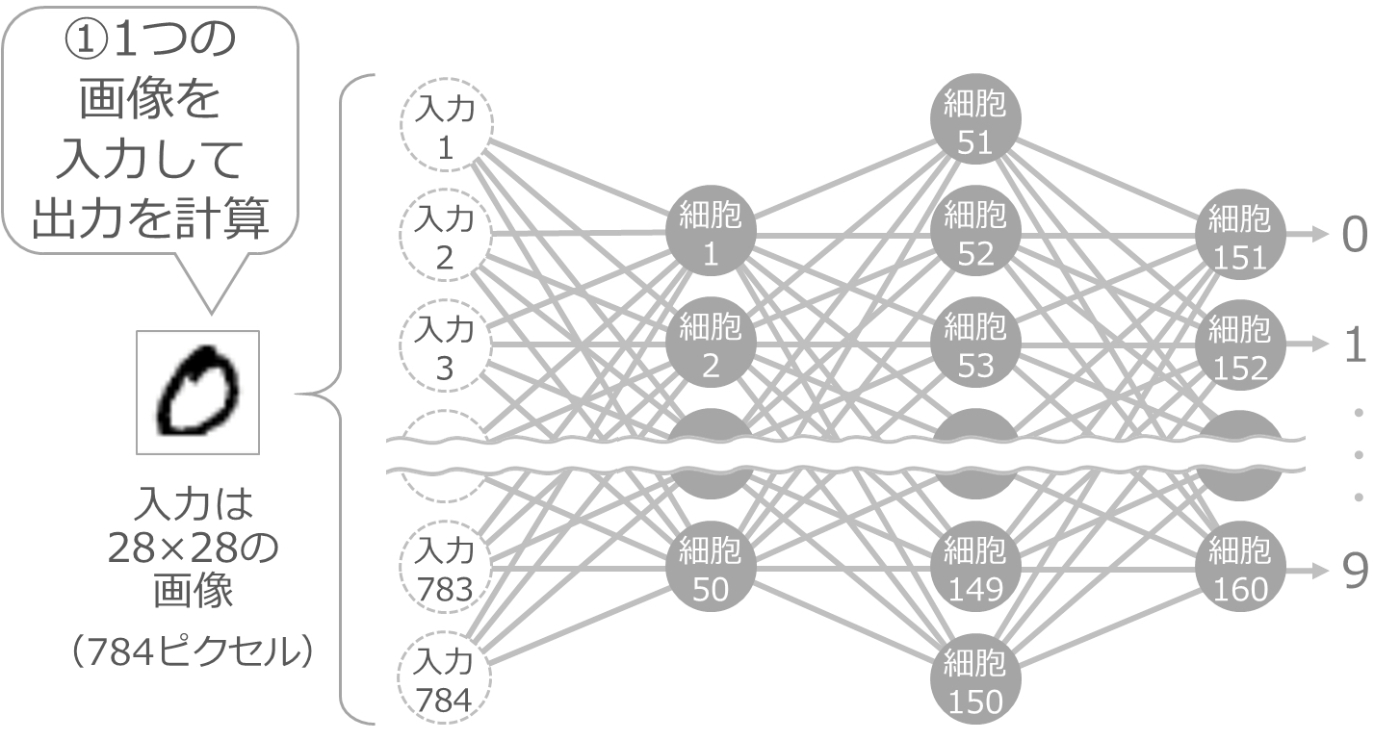
変数がランダムなので、当然ながら正しい出力にはなりません。おそらく、最後の10個の細胞はどれも同じくらいの出力になるかと思います。

次に、入力1と細胞1をつなぐ線の伝わりやすさを、少しだけ大きくしてみます。以下の青い線の部分です。

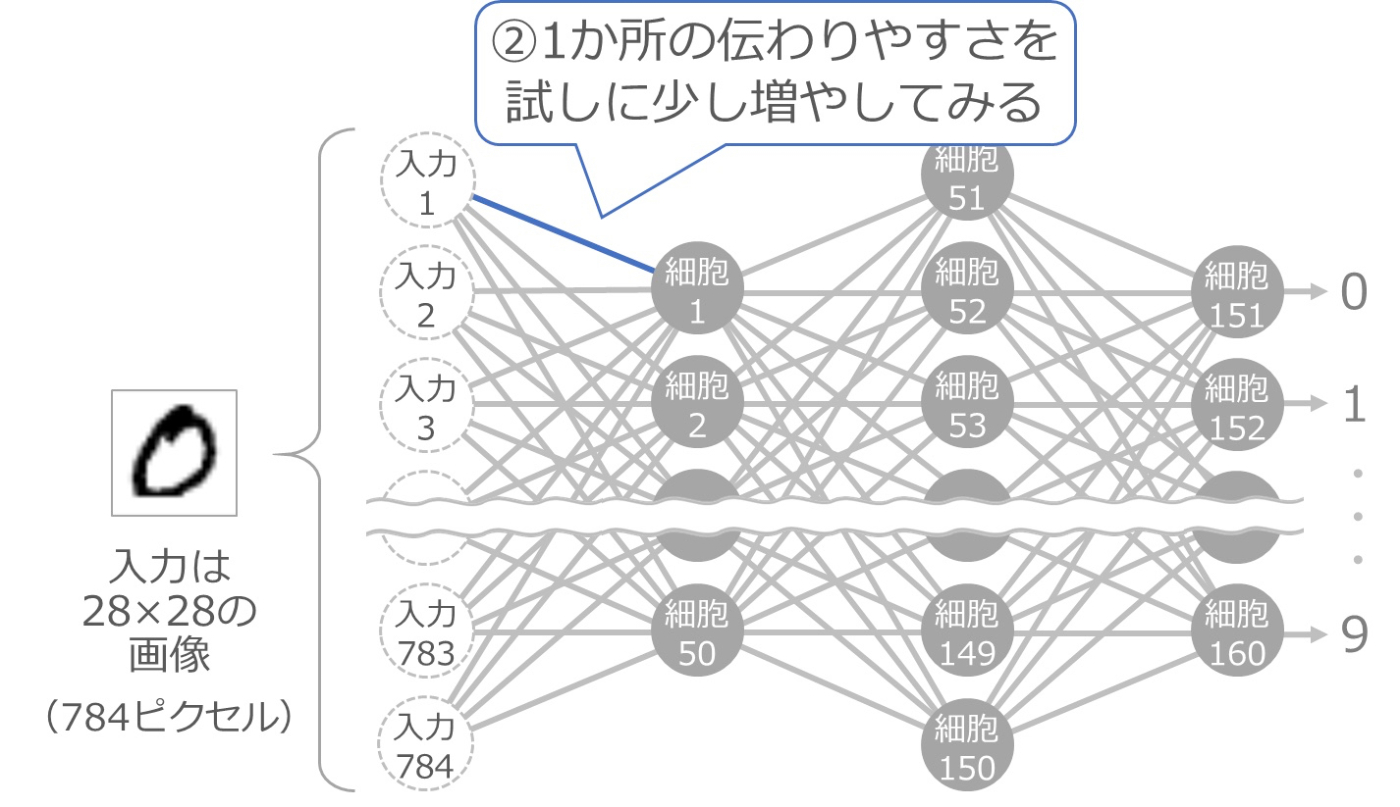
少し大きくすると、それ以降の細胞の入力が変化しますので、その部分の計算をやり直します。以下の青い細胞と緑の線の部分が計算のやり直しです。

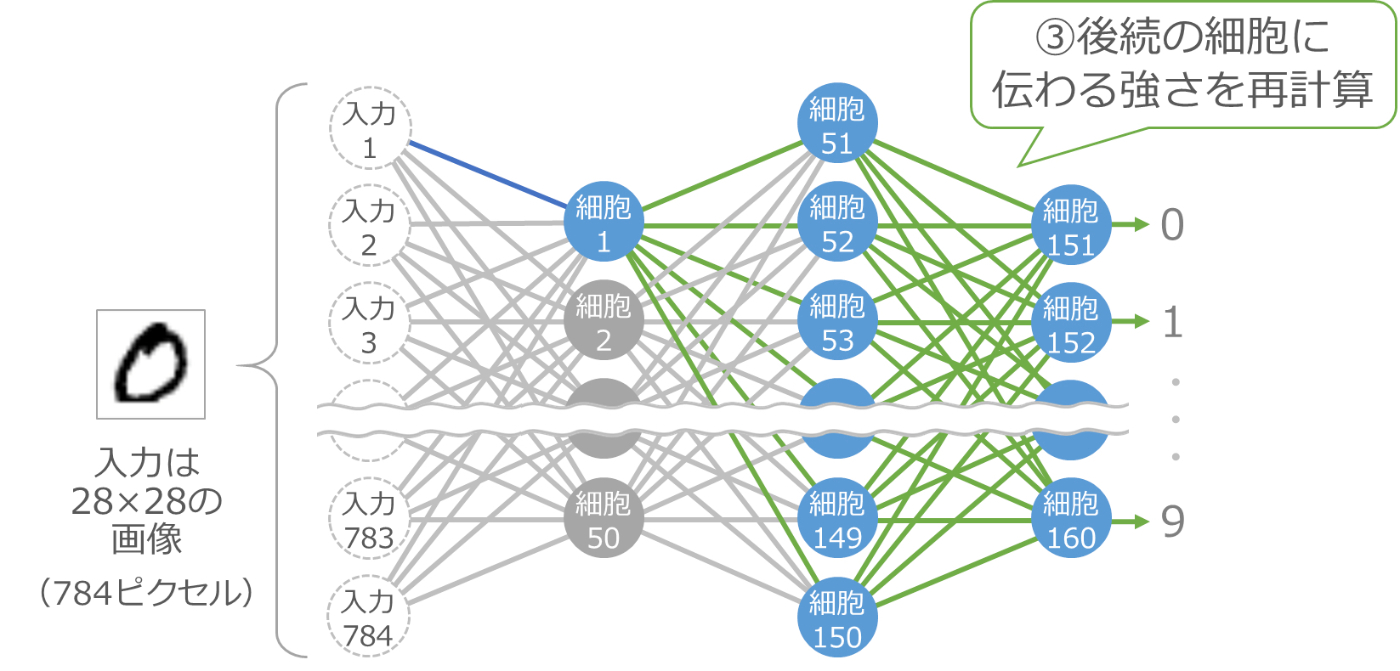
ここで、最後の10個の細胞の出力をチェックします。今は 0 の画像を渡しているので、理想は 0 に対応する細胞151の出力が大きくなって、他の細胞の出力が小さくなることです。そのように変化したかどうかをチェックするわけです。

もし、細胞151の出力が最初に試した時より大きくなったり、他の細胞の出力が小さくなった場合は、入力1と細胞1をつなぐ線の伝わりやすさを大きくしたことが正解だったので、この変数の変更を確定します。そうではない場合は、この変数の変更は失敗だったので、逆に少し小さくすることで確定します。

変数をすべて調整

同じ要領で、すべての変数を調整します。45,200個の伝わりやすさと160個の境界の変数が対象です。

0以外の画像でも調整

数字は 0 だけではないので、1 から 9 の画像も用意して同じ要領で調整します。

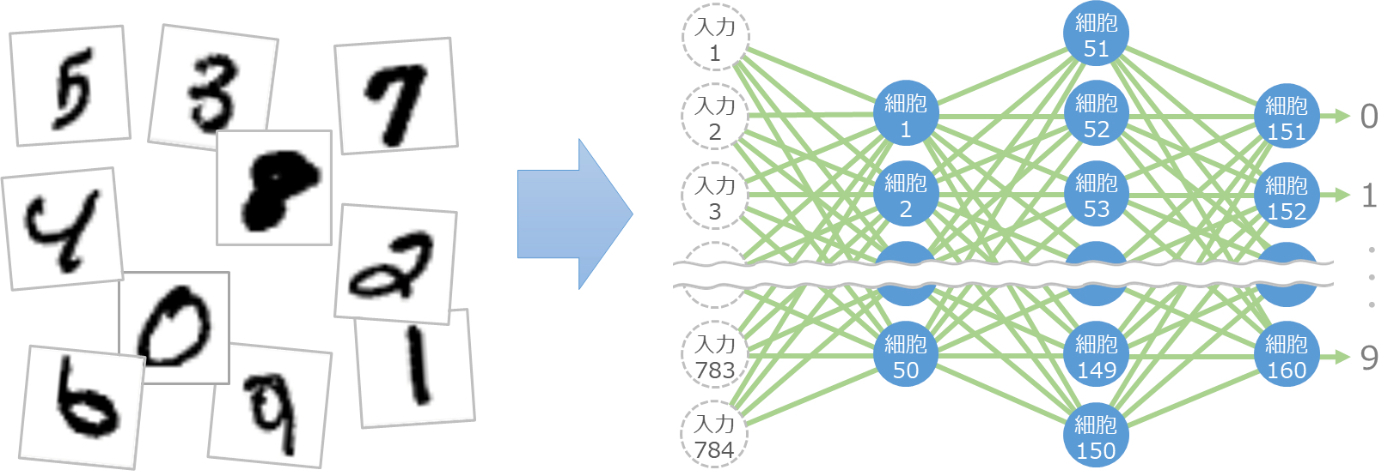
さまざまなバリエーションで調整

手書き数字はいろいろなバリエーションがあるので、各数字の手書き画像をたくさん用意して同じ要領で調整します。

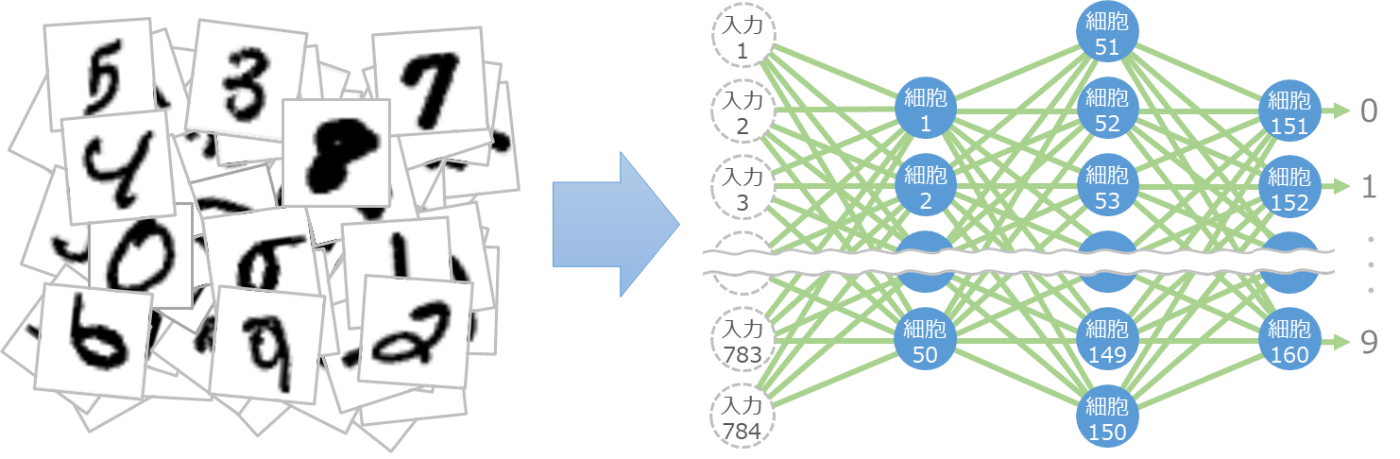
何度も調整

いろんなバリエーションをバランスよく認識できるようにするためには、少しずつの調整を何度も繰り返す必要があります。そのため、用意した画像に対して何度も調整を繰り返し、調整しなくてもだいたい目的の出力が得られるようになったところで止めます。

かなり大変な作業になりますので、ヒトではできません。この作業を実行するプログラムを書いて、コンピューターにがんばってもらうことになります。このように、目的の出力になるように何度も何度も変数を調整していく作業をコンピューターにやらせることを「機械学習」と呼びます。

なお、機械学習による変数の調整は、脳をマネする仕組み以外でも昔から使われています。

実際の調整の工夫

変数の調整は大変時間がかかる作業のため、実際にはいろいろな工夫をしています。その工夫の例を3つご紹介します。

a.出力する値の決め方

各細胞は入力の合計が境界以上なら 1 を出力するとご説明してきましたが、実際にはスパッと 0 と 1 に判定するのではなく、なだらかな判断をしています。

スパッと判定する仕組みでは、調整によって前の細胞からの入力の合計がAからBに変化しても、境界をまたがないと出力が変化しません。出力が変化しないと、そこから先の細胞への入力も変化せず、その調整の正否が判定できなくなってしまいます。下のグラフの緑の線がそれを示しています。

そこでグラフの青い線のように、入力の合計に応じて出力がなだらかに変化する仕組みを使います。こうすれば、入力の合計がAからBに変化した時も出力が変化し、いつでも調整ができるようになります。

b.偏微分の利用

変数の調整は、最終の出力がどう変化するのかを確認しながら実施するため、何度も最終の出力を再計算する必要があります。細胞が増えてくると計算量が現実的ではありません。

そこで、少し数学の話になってしまいますが、偏微分という仕組みを使います。偏微分は式の中のある変数が変わった時に、その式の結果がどう変化するのかを調べるためのものです。最終結果を求める式が偏微分できれば、最終結果を再計算しなくても各変数が調整できるようになるわけです。

詳細は割愛しますが、最終結果を求める式を偏微分できるように組み上げることで、調整作業を大きく効率化しています。

c.行列計算の利用

出力の計算には、各細胞の出力と伝わりやすさの大量の掛け算、そしてその結果の大量の足し算を何度も繰り返す必要があります。これは少し工夫すると行列計算に置き換えることができます。

行列計算は GPU が得意な計算なので、GPU を活用することにより調整にかかる時間を大きく短縮しています。

ここまでのまとめ

  • 細胞を増やせば複雑なことができます。
  • 細胞が増えれば増えるほど大量の変数の調整が必要になりますが、調整はコンピューターにお任せできます。これが機械学習です。

なんでもできそうなご説明になっていますが、実際にはそんなに甘くなく、いろいろな課題があります。ここからはその代表的な課題をご説明します。

3.課題とその取り組み

機械学習は調整のさじ加減が非常に難しく、どうしても試行錯誤が必要になります。そのため、細胞の数を増やしすぎると膨大なマシンパワーや時間が必要になってしまいます。

また、細胞を増やすだけでは十分な精度が出せないテーマもたくさんあります。そのため、細胞そのものの仕組みを改良する研究や、細胞間のつなげ方の研究、他の用途で作った仕組みを組み合わせる研究などが活発に行われています。

いろいろな細胞とそのつなげ方

以下のサイトで、FJODOR VAN VEENさんが主要な仕組みをイラストで紹介しています。ページの先頭にある「Neural Networks」というイラストを軽く眺めてみてください。

https://www.asimovinstitute.org/neural-network-zoo/

これは、主要な細胞の種類とつなぎ方をイラストにしたものです。カラフルな丸が細胞なのですが、いろいろな種類のあることがわかります。また、細胞のつなぎ方も、総当たりだったり間を飛び越していたり循環していたり、いろいろなつなげ方のあることがわかります。

ここでは例として、細胞の出力を自分自身に戻す仕組みと、用途の違う2つの仕組みをつなげた仕組みをご紹介します。

例1: 出力を自分自身に戻す仕組み

これは、細胞の入力を計算する際に、前回計算した自身の出力も混ぜて使う仕組みです。

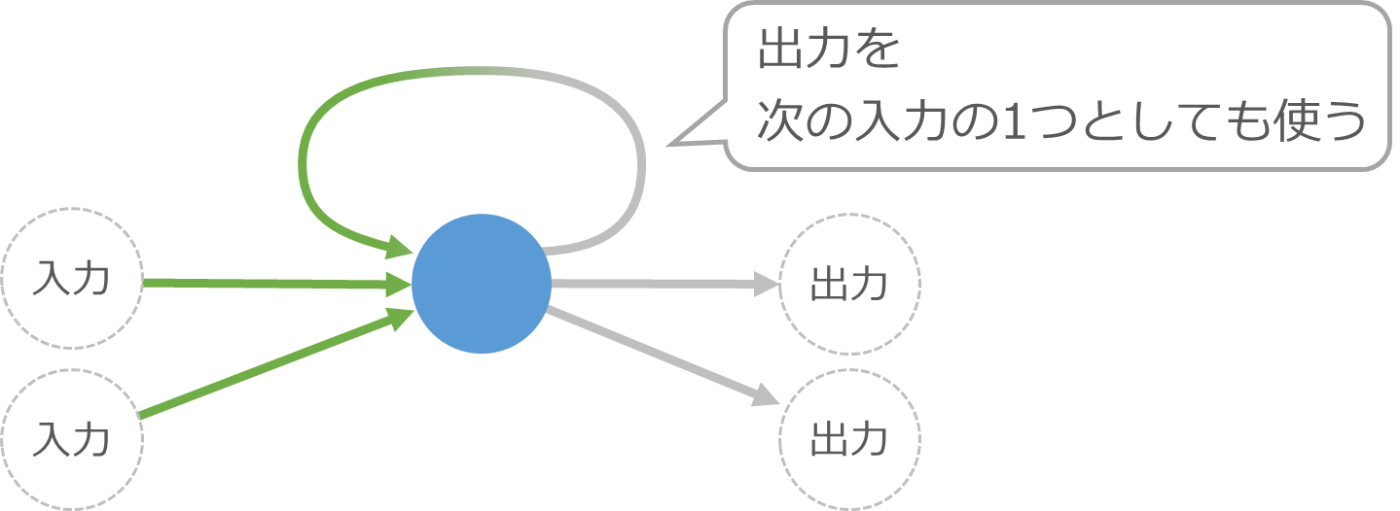
この図だけでは分かりにくいのですが、これで入力の順番を考慮した調整ができるようになります。たとえば、この細胞を使った仕組みに対して実際の小説のデータを機械学習させると、おもしろいことができるようになります。

まず、入力に小説の先頭の単語を与えて、出力がその次の単語になるように調整します[2]。夏目漱石の「吾輩は猫である」の場合、まず「吾輩」を入力して出力が「は」になるように調整し、次に「は」を入力して出力が「猫」になるように調整していきます。

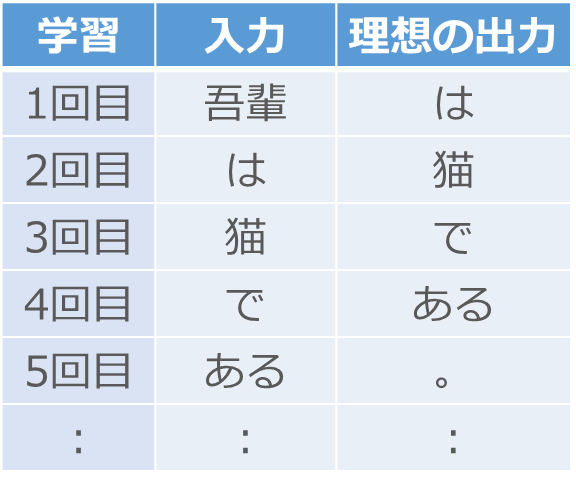
ここでのポイントは、小説の内容通りの順番で単語を入力して調整することです。出力を自分自身に戻す仕組みがあるため、たとえば2回目の「は」→「猫」の調整では、いつでも「は」がきたら「猫」が正しい、と調整されるわけではなく、1回目の「吾輩」の調整で使った細胞の出力が2回目の「は」の入力と混ざることで、「吾輩」と「は」が続く時は「猫」が正しい、という形で調整が進みます。

夏目漱石のさまざまな小説を使ってこのような機械学習を完了させると、小説の書き出しを適当に与えるだけで、続きを執筆してくれる仕組みができあがります。

まず入力に「吾輩」を与えます。何か単語が出力されますが、それは無視して次に「は」を入力します。同じように出力の単語は無視して「犬」を入力します。ここから先は出力で得られた単語をそのまま次の入力として与えていきます。

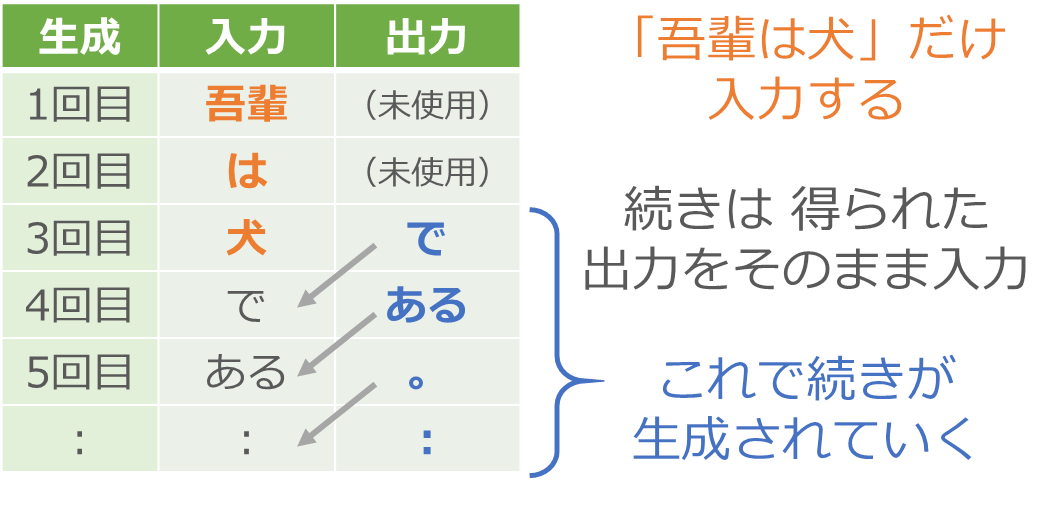
つまり「吾輩は犬」という書き出しを与えたら、あとは得られた出力をそのまま入力に回すことで、次々に文章を生成させていくわけです。夏目漱石の小説には「吾輩は犬」で始まる文はないかと思いますが、脳をマネた仕組みはあいまいな処理ができるので、夏目漱石風の新しい小説を執筆してくれます[3]。

例2: 用途の違う2つの仕組みの組み合わせ

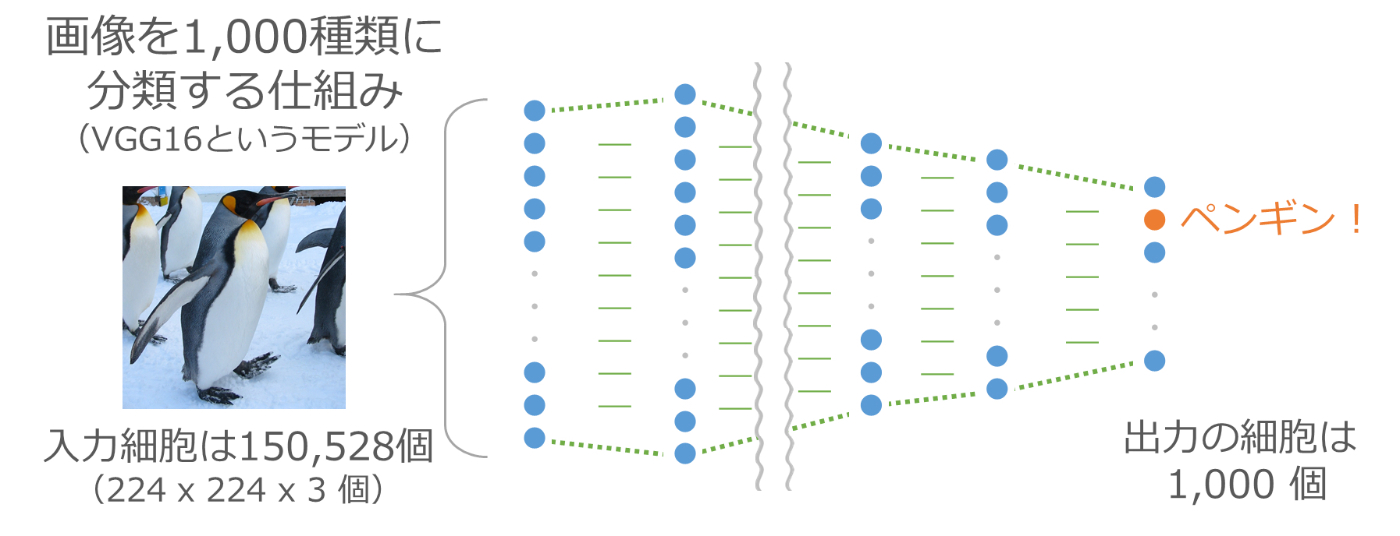
画像を渡すと1,000種類（たとえば「ペンギン」、「消防車」、「オレンジ」、「電球」など）に分類するVGG16という仕組みがあります。縦横それぞれ224ピクセルのカラー画像を渡すと、その画像が1,000種類の中のどれなのかを識別し、何が写っているのかを教えてくれます。手書き数字の認識の発展版のような仕組みです。

最終出力の1つ手前には4,096個の細胞が並びます。この4,096個の細胞の出力が最後の1,000個の入力になっているため、この4,096個の細胞の情報を使って最後の分類が行われています。つまりこの4,096個のデータには、その写真が何であるかを判定するために必要な情報が凝縮されていることになります。

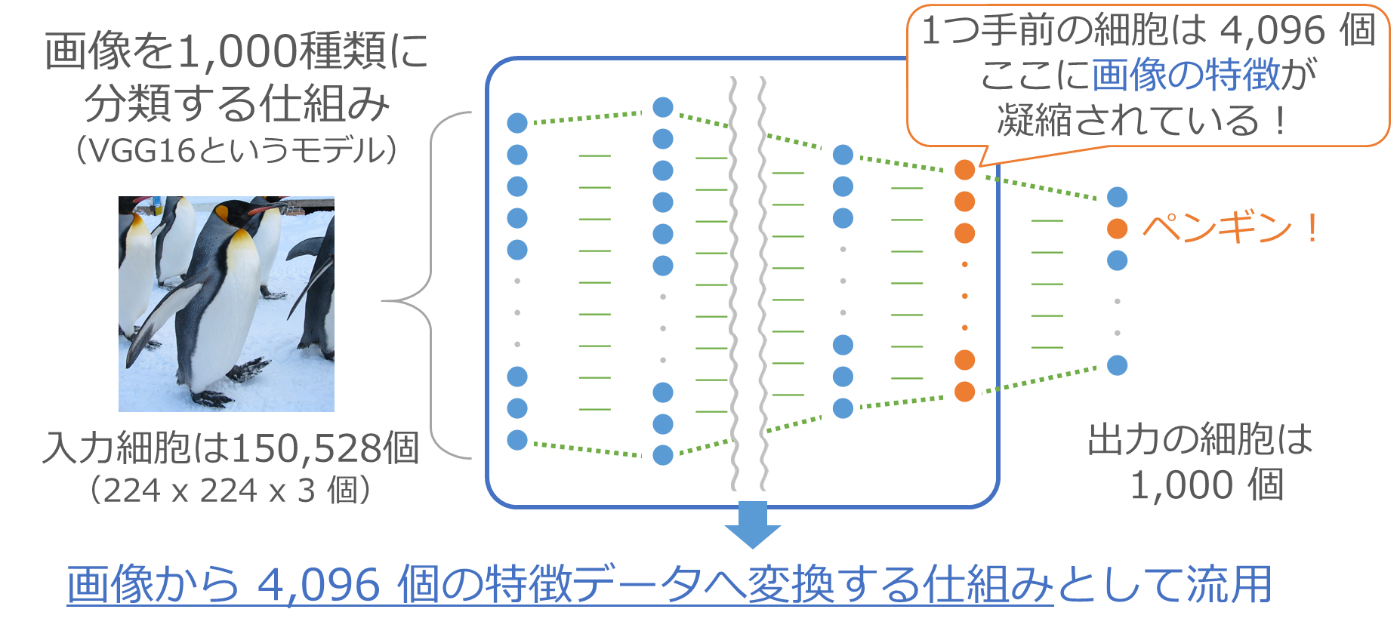
そこで、150,528個ものデータからなる1枚の画像を、特徴を凝縮した4,096個の小さなデータへ変換する仕組みとして上の図の青枠の部分を流用し、先ほどの文章生成の仕組みと組み合わせます。

まず最初に、入力画像を流用した仕組みで4,096個の特徴データに変換します。この部分はすでに機械学習が済んでいるので調整作業は不要です。画像処理部分の機械学習を省くことができることも、この組み合わせの大きなメリットです。

そして、1回目は出力の単語が「ペンギン」になるように調整します。2回目は「ペンギン」を入力して「が」が出力になるように、そして3回目は「が」を入力して「雪」が出力になるようにと、写真の説明文を生成するように調整していきます。

このように、先ほどの文章生成の仕組みと組み合わせて機械学習すると、写真の説明文を生成できるようになります。

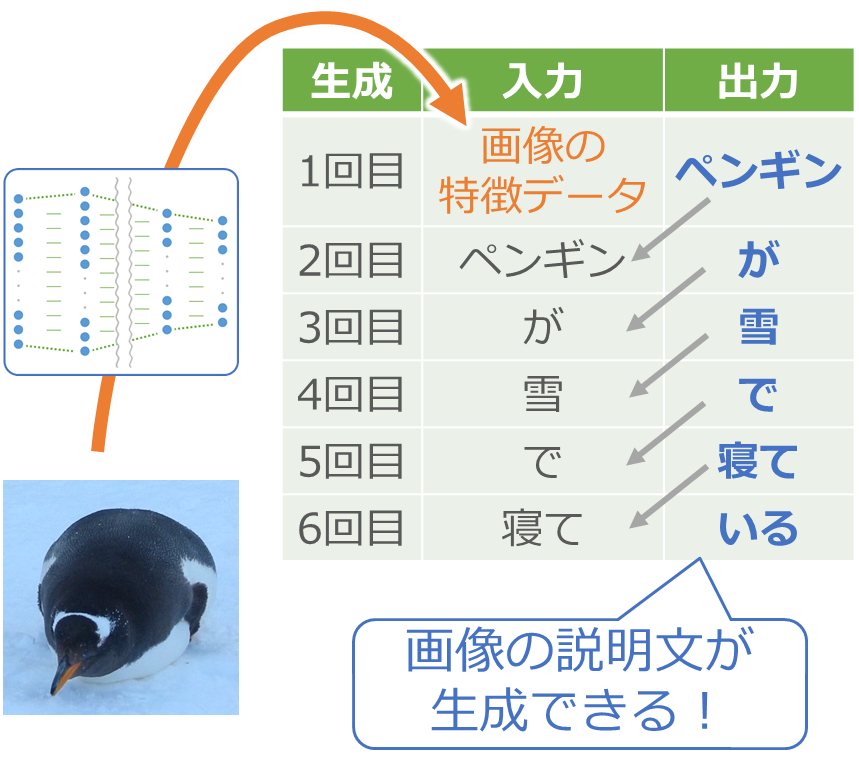
生成させる時は、最初に画像を4,096個の特徴データに変換して入力し、あとは出力で得られる単語を次々に入力に渡していきます。これで写真の説明文が生成されていきます。

このように別の学習済みの仕組みを組み合わせることで、機械学習の時間の短縮しつつできることが増やせます。

4.まとめ

駆け足でしたが、神経細胞をマネした仕組みを複雑に組み合わせて、ヒトみたいなことを実現する仕組みのご説明でした。このような仕組みを「Deep Learning」（ディープ ラーニング）と呼びます。

この記事は、「Deep Learning はヒトみたいなことができるらしいけど、一体どんな仕組みになってるの？」と思われている方に仕組みをざっくりご理解いただくことが目的でしたが、いかがでしたでしょうか。

この記事が、みなさまの Deep Learning の理解の一助になれば幸いです。
最後までお読みいただき、ありがとうございました。

参考文献・Webサイト

脚注

  1. この仕組みで、MNIST データベースと呼ばれる手書き数字画像のデータセットで 90% を越える認識精度が出せます。ただし、実際にはもっと高い精度が必要なため、このような画像認識の処理では「畳み込み」と呼ばれる仕組みを組み合わせることが一般的です（2021年時点）。 ↩︎

  2. 単語は長さが一定ではないため手書き数字の例のような入力はできません。そのため、「単語の埋め込み」という手法などにより、その単語の特性を固定数のデータに変換してから処理するのが一般的です（2021年時点）。 ↩︎

  3. 細胞の出力を自分自身に戻す仕組みだけではあまり良い文章が生成されません。文章の生成は新たな仕組みが次々に考案されており、最近では「GPT-3」という仕組みが注目を浴びています（2021年時点）。 ↩︎

Discussion